Общая химия : учебник / А. В. Жолнин ; под ред. В. А. Попкова, А. В. Жолнина. - 2012. - 400 с.: ил.
|
|
|
|
ЧАСТЬ I. БИОФИЗИЧЕСКАЯ ХИМИЯ. Глава 1. ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ И БИОЭНЕРГЕТИКИ
Термодинамика - единственная физическая теория, относительно которой я уверен, что... она никогда не будет опровергнута.
А. Эйнштейн
1.1. ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА КАК ТЕОРЕТИЧЕСКАЯ ОСНОВА БИОЭНЕРГЕТИКИ. ЗАКОНЫ БИОЭНЕРГЕТИКИ. ПОНЯТИЕ СИСТЕМЫ
В основе жизни лежит обмен веществ, который сопровождается процессами превращения энергии. Для понимания этих процессов необходимы знания основ биоэнергетики и термодинамики.
Науку, изучающую трансформацию энергии в живых системах, называют биоэнергетикой. Теоретической базой биоэнергетики является химическая термодинамика.
Первый закон биоэнергетики
Живая клетка избегает прямого использования энергии внешних ресурсов для совершения полезной работы. Она сначала превращает ее в одну из трех конвертируемых форм энергии. А именно в аденозинтрифос-форную кислоту (АТФ), натриевый потенциал (Δ μNa+), протонный потенциал (Δ μН+), две формы которого представлены на рис. 1.1.
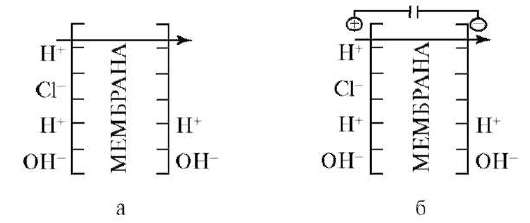
Рис. 1.1: а - градиент кислотности; б - градиент электрического поля
Полученная в организме энергия расходуется на осуществление различных энергоемких процессов и играет роль посредника между процессами запасания и ее транспорта. Простейшим примером конвертации энергии в запас может быть гликолиз или расщепление углеводов до молочной кислоты: углевод + АДФ → молочная кислота + АТФ.
Если АТФ используется для совершения механической работы (у животных для мышечного сокращения), то цепь процессов завершается расщеплением АТФ до АДФ и Н3РО4 сократительным белком актомиозином: АТФ + НОН → АДФ + Н3РО4 + механическая работа. Δ G0 = -29,2 кДж/моль.
Второй закон биоэнергетики
Любая живая клетка всегда располагает как минимум двумя формами энергии: энергией макроэргических связей АТФ и энергией, связанной с мембраной (Δ μН+ либо Δ μNa+). Клетки растений располагают АТФ и Δ μН+. Δ μNa+ может образоваться на плазмолемме и играет подчиненную роль. Животная клетка обладает всеми тремя формами энергии. Для плазмолеммы характерен Δ μNa+, а для внутриклеточных мембран - Δ μН+.
Третий закон биоэнергетики
Энергетические формы могут превращаться одна в другую. Поэтому получение хотя бы одной из них за счет внешних ресурсов достаточно для поддержания жизнедеятельности. Взаимопревращения АТФ, Δ μNa+, Δ μН+ осуществляются специальными ферментами. Взаимопереход АТФ ↔ Δ μNa+ обеспечивается Na+-АТФ-синтазой, превращение АТФ ↔ Δ μH+ катализируется Н+-АТФ-синтазой, а равновесие Δ μH+ ↔ Δ μNa+ осуществляется Н+/Na+-антипортом.
Термодинамика изучает законы взаимного превращения различных видов энергии при химических и физических процессах, связанных с переходом энергии между телами в форме теплоты и работы.
Теплота - неупорядоченная форма передачи энергии в результате контакта непрерывно движущихся микрочастиц. Условием передачи энергии в форме теплоты является наличие температурного градиента, тогда теплота переходит из более горячей области в более холодную.
Работа - упорядоченная форма передачи энергии, связанная с преодолением внешнего сопротивления.
Термодинамика рассматривает поведение и свойства тел, т.е. макроскопических систем, состоящих из большого числа молекул. Предметом изучения термодинамики являются энергия и законы взаимных превращений форм энергии в равновесных системах.
Первый закон термодинамики утверждает, что общий запас внутренней энергии остается постоянным, если отсутствует обмен с окружающей средой, доказывает эквивалентность различных форм энергии.
Энергия (от гр. energeia - деятельность) - одно из основных свойств материи, мера ее движения и взаимодействия; мера перехода одной формы движения в другую; степень изменчивости системы; способность производить работу.
Химическая термодинамика применяет законы термодинамики к изучению состава, свойств и поведения веществ в химических процессах. Она является теоретической основой биоэнергетики. В термодинамике часто используют понятие «термодинамическая система».
Система - это тело или совокупность тел, выделенных из пространства. Все, что окружает систему, называют средой. Часть системы, имеющая одинаковые во всем объеме физические и химические свойства и отделенная от других частей поверхностью раздела, называется фазой.
В зависимости от фазового состава различают: 1) гомогенные системы - состоят из одной фазы (физиологический раствор, плазма крови); 2) гетерогенные системы - состоят из двух фаз или более. На поверхности раздела фаз такой системы некоторые свойства изменяются скачкообразно (суспензия мела в воде, кровь).
В зависимости от характера взаимодействия системы с окружающей средой различают открытые, закрытые, изолированные системы.
Открытые системы могут обмениваться с окружающей средой как веществом, так и энергией. Примерами могут служить живой организм, раствор в открытой колбе, химический завод. Закрытая система может обмениваться с окружающей средой только энергией. Такие системы типичны для химических экспериментов и производств. Раствор химического вещества в колбе с пробкой, промышленные установки и реакторы, спроектированные с учетом исключения загрязнений окружающей среды токсичными веществами. В анатомическом музее препарат в форме изолированного органа тоже представляет собой закрытую систему. В изолированных системах отсутствует всякий обмен с окружающей средой, как веществом, так и энергией. В действительности невозможно устранить обмен теплотой. Поэтому строго изолированных систем не существует. Как некоторое приближение к изолированной системе можно представить жидкость, помещенную в термос.
Количественно свойства системы оценивают термодинамическими параметрами. Состоянием системы называется совокупность условий существования и состава системы.
Равновесное состояние проявляется, когда все свойства системы остаются постоянными во времени и в системе отсутствуют потоки
вещества и энергии. Если свойства системы постоянны, но имеются потоки вещества и энергии, такое состояние называют стационарным.
Сосуд с двумя закрытыми трубками имеет постоянный уровень жидкости - равновесное состояние. Если трубы открыты и уровень постоянен, то через сосуд проходит поток жидкости - стационарное состояние. Живой организм - открытая стационарная система, основные параметры постоянны. Если свойства системы меняются во времени, состояние называется переходным (неравновесным). Переход системы из одного состояния в другое называется процессом. Процессы бывают изобарными - протекающими при постоянном давлении, изохорными - протекающими при постоянном объеме, изотермическими - протекающими при постоянной температуре, адиабатическими - протекающими без передачи теплоты (быстрые химические реакции). По причинности выделяют самопроизвольные и вынужденные процессы.
Для создания таблиц термодинамических свойств веществ особое значение имеет выбор стандартного состояния. Стандартным состоянием вещества считается устойчивая форма вещества при стандартных условиях: температуре 298,15 K (25 °С) и давлении 105 Па (750,06 мм рт. ст.). Также выделяют так называемые нормальные условия для газов: температуру 273,15 K (0 °С) и давление 101325 Па = 1 атм. (760 мм рт. ст.). Стандартным состоянием раствора считается раствор, находящийся в стандартных условиях и имеющий концентрацию растворенного вещества 1 моль/л.
1.2. ФУНКЦИИ СОСТОЯНИЯ СИСТЕМЫ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ. ВНУТРЕННЯЯ ЭНЕРГИЯ.
ЭНТАЛЬПИЯ
От термодинамических переменных параметров состояния зависят различные свойства системы, которые называются функциями состояния. К ним относятся внутренняя энергия (U или Е), энтальпия (H), энтропия (S), свободная энергия [энергия Гиббса (G)] и др. Они зависят от термодинамических параметров, но не зависят от способа, которым это состояние достигнуто.
Каждая система обладает определенным запасом энергии, называемой внутренней энергией. Внутренняя энергия системы (U) представляет собой сумму энергий всех видов движений (поступательного, вращательного, колебательного) частиц системы (молекул, ионов, ядер).
Внутренняя энергия - это полная энергия системы за вычетом потенциальной, обусловленной воздействием на систему внешних силовых полей (в поле тяготения), и кинетической энергией движущейся системы.
Запас внутренней энергии определяется природой вещества, его массой и состоянием системы.
Полную внутреннюю энергию (абсолютное значение внутренней энергии) определить невозможно. Экспериментально можно определить только изменение внутренней энергии при переходе ее из одного состояния в другое:

где U1 и U2 - внутренняя энергия начального (исходного) и конечного состояний, и называется приращением внутренней энергии.
Теплота, подведенная к закрытой системе, расходуется на изменение внутренней энергии системы и совершение работы - формулировка первого закона термодинамики, для процесса, протекающего при постоянном давлении, который является законом сохранения энергии и описывается уравнением:

где Qp - теплота изобарного процесса; ΔU - приращение внутренней энергии; W - работа.
Уравнение (1.2) представляет математическое выражение первого закона термодинамики для процесса, протекающего при постоянном давлении (изобарный процесс).
Впервые понял и доказал эквивалентность понятий теплоты и работы и сформулировал первое начало термодинамики (1842) немецкий врач Р. Майер (1814-1878). В любом процессе изменение внутренней энергии системы равно сумме количества переданной теплоты и совершенной работы.

Вместо суммы в правой части уравнения (1.3) мы видим разность, что является следствием принятой системы знаков. В термодинамике обычно принимается, что теплота, отданная системой в окружающую среду, отрицательна, а полученная системой из окружающей среды - положительна. Для работы приняты противоположные знаки. Работа, совершенная системой над окружающей средой, - положительна, а работа, совершенная со стороны окружающей среды над системой, - отрицательна.
При постоянном давлении меняется объем и становится неизбежной работа расширения (сжатия):

где ΔV = V2 - V1 - приращение объема системы, равное разности объемов в системе.
Подставив в уравнение (1.2) величину работы расширения (сжатия), получим следующее уравнение:

Исходя из уравнения (1.5), энтальпия - это функция состояния системы, приращение которой равно теплоте, полученной системой в изобарном процессе. Энтальпия описывается уравнением:

Абсолютное значение величины энтальпии, как и внутренней энергии, измерить невозможно, поэтому измеряют изменение энтальпии в ходе процесса. Энтальпия отличается от внутренней энергии, на работу расширения рΔV:

При изучении возможности самопроизвольного протекания процесса была выявлена закономерность: система стремится к переходу в состояние с наименьшей энергией (при изобарном процессе). Данную тенденцию называют энтальпийным фактором. Процесс самопроизвольно протекает в сторону выделения теплоты (принцип Бертло), т.е. при значении АЕ и АН реакции меньше нуля (АЕ <0 и АН <0).
Работа расширения процесса, протекающего при постоянном объеме (изохорный процесс), равна нулю, поэтому уравнение (1.2) будет иметь для изохорного процесса следующий вид:

Уравнение (1.8) представляет математическое выражение первого закона термодинамики для процесса, протекающего при постоянном объеме (изохорный процесс).
Следовательно, внутренняя энергия - это функция состояния системы, приращение которой равно теплоте, полученной системой в изохорном процессе.
1.3. ЭНТРОПИЯ. ЭНТАЛЬПИЙНЫЙ И ЭНТРОПИЙНЫЙ
ФАКТОРЫ
Второй закон термодинамики
Функции «внутренняя энергия» и «энтальпия» не дают однозначного ответа на вопрос о возможности самопроизвольного протекания процесса.
Из уравнения (1.3.) следует, что при изменении внутренней энергии системы максимальному значению работы будет соответствовать минимальное значение теплоты (по абсолютной величине). Отношение этой минимально возможной теплоты к температуре, при которой осуществляется изотермический процесс, называется приведенной теплотой.
Энтропия представляет собой функцию состояния систем, приращение которой (ΔS) равно теплоте Qмин), подведенной к системе в изотермическом процессе, деленной на абсолютную температуру (Т), при которой осуществляется процесс:

где Qмин - минимальное приращение теплоты, подведенное к системе.
Уравнение (1.9) является математическим выражением второго закона термодинамики. Знак «>» соответствует необратимому (реальному) процессу, а знак «=» - обратимому (идеальному). Единицы измерения энтропии [Дж/К].
Основная идея, заложенная во втором начале термодинамики, заключается в неизбежности диссипации энергии в форме теплоты по причине асимметрии переходов теплота работа и работа теплота на молекулярно-кинетическом уровне.
Различные виды энергии стремятся превратиться в теплоту, а теплота стремится рассеяться, т.е. теплоту нельзя полностью превратить в работу - формулировка второго закона термодинамики.
Так была выявлена закономерность: система стремится к переходу из более упорядоченного (менее вероятного) состояния в менее упорядоченное (более вероятное).
Энтропию представляют как меру неупорядоченности системы, а количество переданной системе теплоты оценивают произведением ТΔS и называют энтропийным фактором:

Передача энергии в форме теплоты характеризуется произведением двух факторов: интенсивного - T (зависящего от величины самого
фактора) и экстенсивного ΔS (зависящего от длительности процесса и размеров системы).
Энтропия зависит от агрегатного состояния вещества. При переходе веществ из газообразного состояния в твердое энтропия уменьшается:
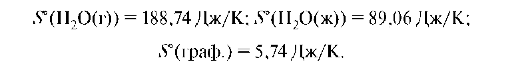
При испарении, диффузии, растворении кристаллов, при химических взаимодействиях приводящих к увеличению числа частиц объема, энтропия процесса увеличивается. При плавлении льда энтропия системы увеличивается примерно в 1,5 раза, а при переходе воды в пар - в 4 раза.
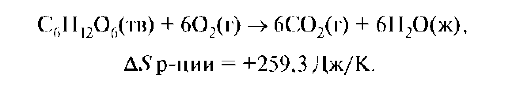
Из 7 молекул образуется 12. Энтропия возрастает и способствует самопроизвольному протеканию процесса (ΔS >0).
Переход систем из менее упорядоченного состояния в более упорядоченные (конденсация, сжатие, полимеризация) приводит к уменьшению энтропии (ΔS <0) и противодействует самопроизвольному протеканию процесса.
Мировоззренческое значение второго начала термодинамики велико. Рост энтропии означает старение Вселенной как изолированной системы и прекращение самопроизвольных процессов при достижении максимальной энтропии. В. Оствальд считал, что сущность живого определяется специфичностью проявления закона рассеяния энергии: живое отличается от неживого большей скоростью приращения энтропии. Русский физик Н. Умов отмечал, что все органы чувств организма, воспринимают сигналы внешней среды за счет действия закона рассеяния энергии. Критика второго начала послужила толчком для развития неравновесной термодинамики и синергетики, привлекла внимание к проблемам глобальной экологии и эволюции.
Итак, система стремится к состоянию с минимальной энергией (АН <0 и Е <0) и максимальной неупорядоченностью системы (ΔS >0). При других сочетаниях характера изменений функций состояния системы возможность самопроизвольно протекающего процесса определяет либо энтальпийный, либо энтропийный фактор. В качестве критерия самопроизвольности процесса введена новая функция - свободная энергия.
1.4. ЭНЕРГИЯ ГИББСА. ХИМИЧЕСКИЙ ПОТЕНЦИАЛ. ЭКЗЭРГОНИЧЕСКИЕ, ЭНДЭРГОНИЧЕСКИЕ И СОПРЯЖЕННЫЕ РЕАКЦИИ
Свободная энергия (энергия Гиббса) - это функция состояния системы, изменение которой равно полной работе процесса за вычетом работы расширения:

Подставляя выражение (1.7), получаем уравнение Гиббса:

Единицы измерения - кДж/моль. Слагаемое АН называется энталь-пийньм членом, слагаемое ТΔS - энтропийным членом. В конкретных реакциях возможно любое сочетание знаков для ΔН и ΔS.
ΔН <0 и ΔS >0 способствует самопроизвольному протеканию процесса;
ΔН >0 и ΔS <0 препятствует самопроизвольному протеканию процесса.
На основе энергии Гиббса второе начало термодинамики можно выразить следующим образом: в изобарно-изотермических условиях (Р, Т - const) в системе самопроизвольно могут осуществляться только такие процессы, в результате которых энергия Гиббса системы уменьшается.
Условие ΔG <0 означает, что реакция идет самопроизвольно в закрытой системе при условии уменьшения энергии Гиббса. В состоянии равновесия энергия системы не изменяется (ΔG = 0).
Работа, производимая системой в необратимом процессе, всегда будет меньше работы, производимой в обратимом процессе. Открытые системы обмениваются с окружающей средой энергией и массой. Поэтому для них ΔG является не только функцией Т, Р, V, но и функцией концентрации компонентов системы.
Свободная энергия (энергия Гиббса) системы может быть рассчитана как сумма энергий Гиббса, составляющих систему частиц, компонентов системы. Для таких расчетов используется химический потенциал вещества (μ ).
Химическим потенциалом вещества в данной системе называется величина, определяемая энергией Гиббса, приходящейся на моль этого вещества при заданных условиях:

где μ (Х) - химический потенциал вещества (X), Дж/моль; G(Х) - энергия Гиббса вещества (X), Дж/моль; n(X) - количество вещества (X), моль.
В идеальных растворах, в которых силы межмолекулярного взаимодействия между всеми частицами идентичны, химический потенциал зависит от концентрации:
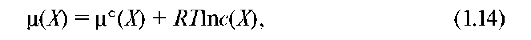
где μ °(Х) - стандартный химический потенциал при с = 1 моль/л.
В реальных растворах химический потенциал зависит от величины активности, связанной с концентрацией следующим соотношением: a = fc, где f - коэффициент активности.
Если в системе несколько веществ (A, B и т.д.) в количестве nA, nB, то энергия Гиббса системы определяется суммой энергий Гиббса, составляющих систему веществ:
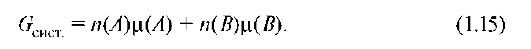
Поскольку большая часть биохимических процессов идет с участием катионов водорода, физиологическое значение pH близко к 7. В связи с этим стандартная свободная энергия в биохимии обозначается АО', разность между ΔG° и ΔG' составляет 39,95 кДж/моль (ΔG' = ΔG° + + 39,95 кДж/моль).
В физике также используется понятие свободной энергии Гельмгольца. Свободная энергия Гельмгольца является мерой полной работы, которую может совершить термодинамическая система над внешними телами:

Классификация реакций в зависимости от величины приращения энергии Гиббса реакции (AG)
1. Реакции, при протекании которых происходит уменьшение энергии Гиббса и совершается работа, называют экзэргоническими.
Например, ΔGo реакции окисления глюкозы равна -2880 кДж/ моль;
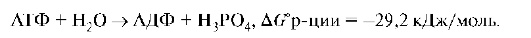
2. Реакции, в результате протекания которых энергия Гиббса возрастает (ΔG >0) и совершается работа над системой, называют эндэр-гоническими.
Например, процесс фотосинтеза:
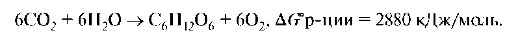
3. Сопряженные реакции. Первая стадия гликолитического обмена:
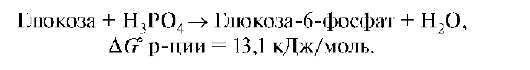
Это эндэргоническая реакция, она протекает в живых организмах, так как работает принцип энергетического сопряжения. Она сопряжена с экзэр-гонической реакцией гидролиза АТФ. Суммарно можно записать:
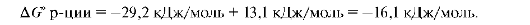
Этот пример сопряжения типичен для многих биологических процессов. Сопряженные реакции - это реакции, в которых экзэргонический характер одной из реакций обеспечивает протекание до конца другой эндэргонической реакции через образование промежуточных соединений.
В нашем примере сопряженная реакция осуществляется в результате образования промежуточного соединения - фосфорной кислоты, которую называют интермедиатом. Если же ΔG = 0, то система находится в состоянии химического равновесия. Направление такой реакции определяется только концентрацией отдельных компонентов. Подобный процесс имеет место при аккумулировании энергии в мышечной ткани.
1.5. ТЕРМОХИМИЯ. ЗАКОНЫ ТЕРМОХИМИИ, ИХ СЛЕДСТВИЯ. ТЕРМОХИМИЧЕСКИЕ РАСЧЕТЫ
Раздел химической термодинамики, изучающий тепловые эффекты реакций, называется термохимией.
Теплота, которая выделяется или поглощается при протекании данной реакции, называется ее тепловым эффектом. Величина теплового эффекта зависит от природы участвующих в реакциях веществ, их количества, условий протекания реакции (Т, р).
Таким образом, при изохорном процессе тепловой эффект реакции равен изменению внутренней энергии системы, а при изобарном - изменению энтальпии системы. В зависимости от теплового эффекта реакции делятся на экзо- и эндотермические.
Экзотермические реакции - реакции, сопровождающиеся выделением теплоты, при этом происходит уменьшение внутренней энергии и энтальпии.
При этом:
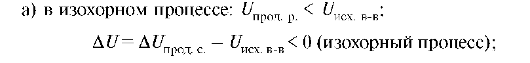
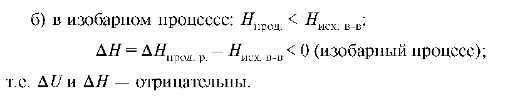
Эндотермические реакции - реакции, сопровождающиеся поглощением тепла, при этом происходит увеличение внутренней энергии и энтальпии. При этом:
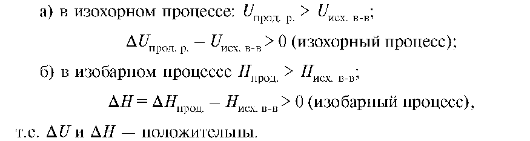
Уравнения реакций, для которых указывается их тепловой эффект, называются термохимическими. Тепловой эффект реакции необходимо характеризовать не только величиной, но и знаком. Исторически сложились две системы отсчетов: термохимическая и термодинамическая. В первой из них тепловой эффект экзотермической реакции считается положительным, эндотермической реакции - отрицательным тепловым эффектом. В термодинамике принята обратная система знаков, т.е. теплота, поглощенная системой, считается положительной, так как внутренняя энергия и энтальпия системы увеличиваются, а теплота, отданная системой, - отрицательной, так как внутренняя энергия и энтальпия уменьшаются. Следовательно тепловой эффект эндотермической реакции положителен, а экзотермической - отрицателен. Тепловые эффекты реакций определяют как экспериментально, так и с помощью термохимических расчетов.
Для сравнения тепловых эффектов различных процессов расчеты относят к 1 молю соединения, выражают в кДж/моль, записывают стандартные изменения соответствующих величин с индексом «°» сверху (ΔН°СО2 = -393,5 кДж/моль). То количество теплоты, которое выделяется или поглощается при образовании 1 моля сложного вещества из простых веществ, в термохимии называется теплотой образования данного вещества. Чаще теплота образования обозначается ΔНf (formation - образование). Энтальпия образования СН3ООН есть ΔНf реакции образования 1-го моля СН3ООН из 2 моль Н2, 1 моль О2 и 2 моль графита. Запишем термохимичское уравнение реакции образования воды с термодинамической системой отсчета:
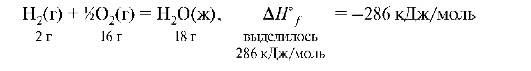
Образование 1 моля Н2О(ж) из простых веществ при стандартных условиях сопровождается изменением энтальпии данной реакции на 286 кДж/моль. Стандартные теплоты образования вещества равны по абсолютной величине и противоположны по знаку изменению стандартной энтальпии образования этого же вещества. Следовательно, эта реакция сопровождается выделением 286 кДж/моль. ΔН - отрицательная величина (<0), следовательно, реакция экзотермическая.
Запишем термохимическое уравнение с термохимической системой отсчета:
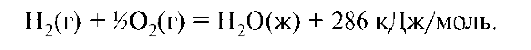
Величина и знак теплоты образования характеризуют термодинамическую устойчивость соединения в данных условиях.
Количество теплоты, выделяемое или поглощаемое при разложении одного моля сложного вещества на более простое, называется теплотой разложения. Например, теплота разложения СаСО3 - 177,9 кДж/моль.
Теплотой сгорания называется тепловой эффект реакции окисления одного моля данного вещества кислородом до образования высших оксидов.
Если известны теплоты сгорания всех веществ, участвующих в реакции, то по ним можно рассчитать и тепловой эффект самой реакции. В основу термохимических расчетов положены законы, которые практически являются следствием закона сохранения и превращения энергии (1-й закон термодинамики).
В 1784 году Лавуазье и Лаплас открыли 1-й закон термохимии: при образовании соединения поглощается (или выделяется) такое количество теплоты, которое выделяется (или поглощается) при его разложении на исходные составные части:
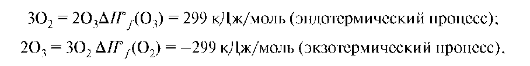
т.е. теплота разложения соединения равна по абсолютной величине и противоположна по знаку теплоте его образования.
Важнейшим законом, лежащим в основе многих термодинамических расчетов, является 2-й закон термохимии - закон суммы тепловых эффектов, открытый и экспериментально подтвержденный русским
академиком Г.И. Гессом (врач и химик) в 1840 году (в настоящее время рассматривается как следствие 1-го закона термодинамики): тепловой эффект химической реакции, т.е. изменение энтальпии и/или внутренней энергии системы при постоянном давлении и температуре, зависит только от начального и конечного состояния реагирующих веществ и не зависит от пути (способа получения), по которому протекает реакция.
Например, СО2 можно получить, непосредственно сжигая С (графит) в О2 или сначала сжигать его до СО, а затем до СО2. Эти два пути можно изобразить в виде следующей схемы:
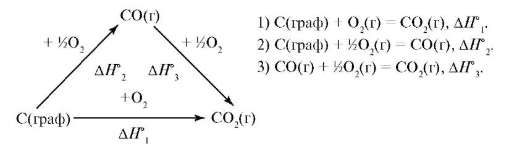
Согласно закону Гесса, тепловые эффекты образования СО2 как непосредственно из простых веществ, так и через промежуточную стадию образования СО равны: ΔН°1 = ΔН°2 + ΔН°3, - зная две величины этого равенства, можно определить третью. Тепловые эффекты образования СО2(ΔН°1) и горения СО(ΔН°3) определяются экспериментально. Тепловой эффект образования СО(ΔН°2) измерить невозможно, но его можно рассчитать по известному значению ΔН°1 = (-396 кДж/моль) и ΔН°3 = (-285 кДж/моль). Н°2 = ΔН°1 - ΔН°3, ΔН°2 = (-396) - (-285) = -111 кДж/моль.
Исходя из этого можно вывести правило, применение которого упрощает многие термохимические расчеты. При суммировании следует учитывать число молекул, участвующих в реакции веществ в соответствии с уравнением.
Функции образования реакции (ΔHo, S и ΔG°) равны алгебраической сумме функций образования продуктов реакции за вычетом алгебраической суммы образования этих функций исходных веществ с учетом их сте-хиометрических коэффициентов в уравнении реакции.
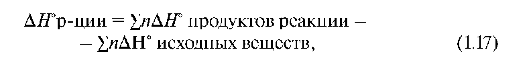
где n - стехиометрические коэффициенты в уравнении реакции.
Для вычисления стандартных энтальпий реакций с участием органических веществ чаще используют значения стандартных энтальпий сгорания:
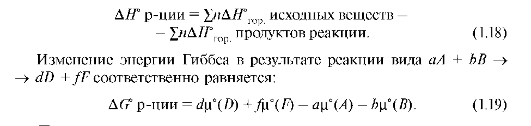
Пример. В клетках организма протекает реакция окисления глюкозы. Определить тепловой эффект реакции.
Окисление глюкозы протекает через целый ряд стадий, но ее можно представить как реакцию полного окисления:
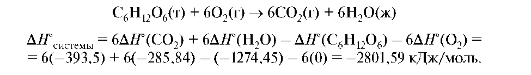
Реакция окисления глюкозы экзотермическая.
Закон Гесса широко применяется в медицине для определения калорийности продуктов питания. Теплота сгорания пищевых продуктов определяется в калориметрах. Калорийность (теплота сгорания) жира равна 37 600 кДж/1 кг, углеводов (сахар) - 17 400 кДж/1 кг, белков - 16 700 кДж/1 кг. Жиры и углеводы должны давать примерно 12 500 ккал, необходимых человеку ежедневно. В настоящее время теплоты образования известны примерно для 6000 веществ, и это позволяет расчетным путем установить эффект самых разнообразных реакций и установление калорийности основных пищевых продуктов.
1.6. ВОПРОСЫ И ЗАДАЧИ ДЛЯ САМОПРОВЕРКИ
ПОДГОТОВЛЕННОСТИ К ЗАНЯТИЯМ И ЭКЗАМЕНАМ
1. Дайте определение понятиям «система», «состояние системы».
2. Классификация систем в зависимости от характера их взаимодействия с окружающей средой.
3. Приведите примеры открытых, закрытых и изолированных систем медико-биологического профиля.
4. Дайте определение стационарного, равновесного и переходного состояний системы. Привести примеры.
5. Изобарные и изохорные процессы.
6. Приведите примеры изобарных, изохорных и изотермических процессов. Какой тип процессов рассматривается в основном в термодинамических моделях живых систем? 0бъясните почему.
7. Дать понятие термодинамических параметров системы.
8. Перечислите основные функции состояния системы. Покажите, что они зависят от термодинамических параметров, но не зависят от способа, которым это состояние достигнуто.
9. Приведите математическое выражение 1-го и 2-го законов термодинамики.
10. Дайте определение понятиям «внутренняя энергия» и «энтальпия».
11. Чем отличается энтальпия от внутренней энергии?
12. Какая функция состояния системы является показателем принципиальной возможности самопроизвольного протекания процесса?
13. Покажите на конкретных примерах применимость первого начала термодинамики к биосистемам.
14. 0бъясните, почему закон Гесса является следствием первого начала термодинамики? Докажите справедливость одного из следствий закона Гесса.
15. Что понимается в термодинамике под стандартными условиями?
16. Дайте определение понятиям «энтропия» и «энергия Гиббса».
17. 0бъясните, почему при приближении значения температуры к абсолютному нулю значение энтропии стремится к нулю?
18. К какому типу: а) открытая; б) закрытая; в) изолированная - относится каждая из перечисленных систем:
1) открытая ампула с плазмой крови;
2) закрытая ампула с плазмой крови;
3) ампула с плазмой крови, помещенная в калориметр;
4) человек в барокамере;
5) космический корабль с космонавтами.
19. Почему кристаллогидраты растворяются с поглощением теплоты, в то время как соответствующие безводные соли - с выделением?
20. Самопроизвольный характер процесса определяется изменением: а) энтальпии; б) энтропии; в) свободной энергии Гиббса; г) температуры. Выбрать правильный ответ и обосновать.
21. Чем объяснить, что величина теплоты образования 1-го моля воды в результате реакции нейтрализации сильной кислоты сильным основанием больше, чем величина теплоты при нейтрализации слабой кислоты сильным основанием?
1.7. ТЕСТОВЫЕ ЗАДАНИЯ
1. Стандартные теплоты образования водородных соединений пниктоге-нов имеют нижеприведенные значения. Какое из этих соединений самое термически неустойчивое?
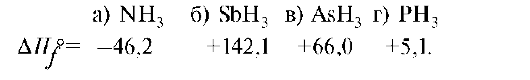
2. Закон Гесса является следствием из:
а) из 1-го закона термодинамики;
б) 2-го закона термодинамики;
в) 3-го закона термодинамики;
г) 0-го закона термодинамики.
3. Если процессы перехода системы происходят при постоянстве давления системы, то они называются:
а) изохорными;
б) изобарными;
в) изотермическими;
г) изобарно-изотермическими.
4. Ученый, создавший термодинамическую абсолютную шкалу температур:
а) А. Цельсий;
б) У. Кельвин;
в) Г. Фаренгейт;
г) Р. Реомюр.
5. Температура является мерой:
а) полной внутренней энергии поступательного движения молекул;
б) средней потенциальной энергии поступательного движения молекул;
в) средней кинетической энергии поступательного движения молекул;
г) полной кинетической энергии поступательного движения молекул.
6. Мерой неупорядоченности состояния системы служит термодинамическая функция:
а) теплота;
б) энтальпия;
в) внутренняя энергия;
г) энтропия.
7. Термодинамическая система является открытой, если она обменивается с окружающей средой:
а) веществом;
б) энергией;
в) веществом и энергией;
г) ни веществом, ни энергией не обменивается.
8. По международной системе СИ в джоулях (Дж) измеряется:
а) масса;
б) температура;
в) энтропия;
г) работа, энтальпия, энергия Гиббса.
9. Условием самопроизвольного протекания процесса реакции является:
а) ΔН <0;
б) ΔS <0;
в) ΔН >0;
г) ΔS>0;
д) ΔG <0.
10. Энтропия системы возрастает при переходе вещества:
а) из кристаллического состояния в жидкое;
б) из газообразного в жидкое;
в) из жидкого в твердое;
г) при конденсации.