Медицинская и биологическая физика: учебник / А. Н. Ремизов. - 4-е изд., испр. и перераб. - 2012. - 648 с. : ил.
|
|
|
|
Глава 2. Элементы теории вероятностей
В теории вероятностей исследуются закономерности, относящиеся к случайным событиям, случайным величинам и случайным процессам. Врачи редко задумываются, что постановка диагноза имеет вероятностный характер и, как остроумно замечено, лишь патологоанатомическое исследование может достоверно определить диагноз умершего человека.
2.1. ОПЫТ С НЕОДНОЗНАЧНЫМИ ИСХОДАМИ. СЛУЧАЙНОЕ СОБЫТИЕ
Теория вероятностей изучает закономерности, присущие опытам с неоднозначными исходами. Так называют опыты, результаты которых невозможно безошибочно предсказать. Например, при игре в рулетку шарик, брошенный на вращающееся колесо, может остановиться в любой из 37 пронумерованных лунок (0, 1, 36), но до остановки колеса номер лунки остается неизвестным.
Опыт и его исходы
Понятия «опыт» и «исход» являются первичными понятиями теории вероятностей.
Опыт - это некоторая последовательность действий, которые выполняются при соблюдении определенных условий.
Исход - это то, что непосредственно получается в результате опыта.
Опыт задан, если указаны условия его выполнения и известно множество всех его возможных исходов, которое обозначают буквой Ω. Например, при игре в рулетку крупье закручивает игровое колесо, бросает на него шарик, ждет остановки колеса и объявляет номер лунки, в которой находится шарик. Перечисленные действия представляют собой описание данного опыта. Исходом опыта является объявленный номер лунки. Множеством всех возможных исходов состоит из 37 чисел: Ω = {0, 1, 2, 36}.
Обратите внимание на то, что в результате каждого опыта появляется только один из всех возможных исходов.
В медицинских исследованиях опыт - это любое обследование пациента, например, определение содержания глюкозы в крови, взятой из вены. Исходом является результат обследования.
Случайное событие
Отдельные исходы опыта, как правило, не имеют самостоятельной значимости. Практический интерес представляют некоторые их совокупности, которые называют событиями. Например, игрок в рулетку может поставить деньги на «четное». Тогда он выиграет, если шарик остановится в лунке с четным номером, и проиграет в противном случае. Конкретный номер лунки значения не имеет. В этом случае есть два события, имеющих практический интерес: «выигрыш» - выпадение четного числа, и «проигрыш» - выпадение нечетного числа. Все остальное - не важно.
Исходы медицинских исследований тоже группируют в значимые события. Например, при определении содержания глюкозы в крови рассматриваются 3 события: данный показатель в норме (3,9-6,4 ммоль/л); ниже нормы; выше нормы. А вот конкретная величина показателя (например, 5,18 ммоль/л) практического значения не имеет. В этом примере событие «в норме» - совокупность всех чисел из интервала (3,9-6,4 ммоль/л).
Случайным событием или просто событием называется некоторая совокупность исходов опыта, имеющая практический интерес. Такие исходы называются благоприятствующими этому событию (или благоприятным для него).
Событие наступает, если результатом опыта является один из благоприятствующих исходов.
В теории вероятностей случайные события обозначаются заглавными латинскими буквами (А, В, С...).
2.2. ДЕЙСТВИЯ НАД СОБЫТИЯМИ. ПРОТИВОПОЛОЖНОЕ СОБЫТИЕ.
НЕСОВМЕСТНЫЕ СОБЫТИЯ
Для того чтобы объяснить, в чем заключается данное событие, необходимо перечислить все возможные исходы опыта (Ω) и указать, какие из них являются благоприятными. В одних случаях сделать это просто, а в других случаях значительно сложнее.
Пусть, например, опыт заключается в том, что стрелок производит по мишени один выстрел. В этом случае возможны только два исхода:
А (попадание) или В (промах). Эти исходы являются простейшими событиями.
Теперь рассмотрим опыт, в котором стрелок производит по мишени два выстрела. В этом случае возможны четыре элементарных исхода:
1) А1 и А2 - два попадания;
2) А1 и В2 - попадание и промах;
3) В1 и А2 - промах и попадание;
4) В1 и В2 - два промаха.
Событию С, состоящему в том, что мишень поражена после двух выстрелов, благоприятствуют три исхода, в которых есть хотя бы одно попадание:
С = {(А1 и А2), (А1 и В2), (В1 и А2)}.
Для описания сложных событий их представляют как результат операций (действий) над более простыми событиями. К таким операциям относятся сложение и произведение событий.
Суммой или объединением двух событий А и В называется событие, состоящее в наступлении хотя бы одного из них.
Сумма событий обозначается следующим образом: А + В. (В некоторых учебниках сумма событий обозначается А U В.)
Событие А + В представляет собой совокупность исходов, благоприятных хотя бы одному из событий А, В.
Произведением или пересечением двух событий А и В называется событие, состоящее в наступлении их обоих.
Произведение событий обозначается следующим образом: А-В. (В некоторых учебниках пересечение событий обозначается А Π В.)
Событие А-В представляет собой совокупность исходов, благоприятных для каждого из событий (и для события А и для события В).
Рассмотренное выше сложное событие С - поражение мишени двумя выстрелами - записывается с помощью операций сложения и умножения простых событий (А - попадание, В - промах) следующим образом:
С = А1-А2 + А1-В2 + В1-А2.
Разберем простой пример, поясняющий технику выполнения операций сложения и умножения событий. Бросается игральный кубик. Событие А - выпадение четного числа: А = {2, 4, 6}. Событие В - выпадение числа, кратного трем: B = {3, 6}.
• Сложение: А + В - это выпадение числа, которое или является четным, или делится на 3: А + В = {2, 3, 4, 6}.
• Произведение: АВ - это выпадение числа, которое является и четным, и делится на 3: АВ = {6}.
Действия над событиями удобно иллюстрировать графически с помощью специальных диаграмм Вена. На этих диаграммах пространство элементарных исходов Ω изображается некоторым кругом, точки которого интерпретируются как элементарные исходы. Простые события изображаются какими-либо фигурами, например, овалами. Изображение суммы и произведения событий показано на рис. 2.1 (темная область).
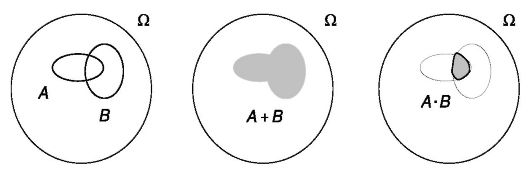
Рис. 2.1. Графическое изображение суммы и произведения двух событий
Противоположное событие
Каждому событию А можно поставить в соответствие противоположное ему событие А (читается «не А»), состоящее из всех исходов, неблагоприятных для А. Графическая иллюстрация событий А и А представлена на рис.2.2
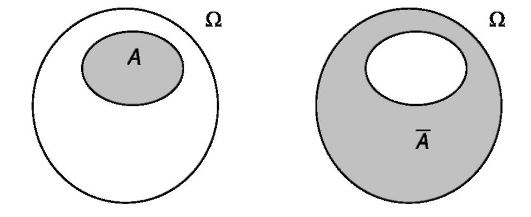
Рис. 2.2. Событие А и противоположное ему событие А
Событие, противоположное событию А, состоит в том, что при выполнении опыта событие А не наступило. Отметим, что А + А = Ω.
Несовместные события
Важное место в теории вероятности занимают несовместные события.
Несовместными называются события, которые не могут произойти одновременно (при выполнении одного опыта).
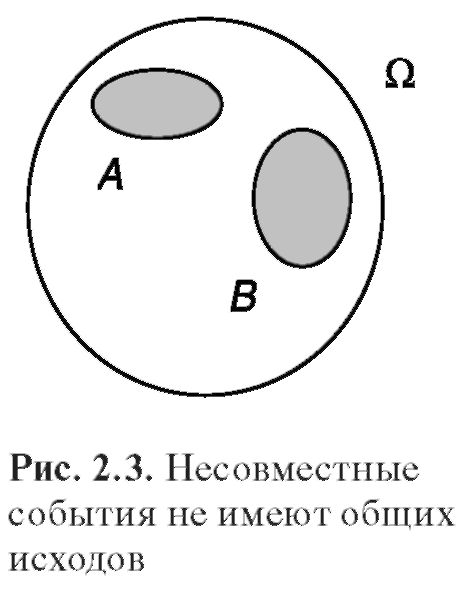
У несовместных событий нет общих исходов, поэтому они изображаются непересекающимися фигурами (рис. 2.3).
Важным частным случаем несовместных событий являются прямое и противоположное события (А и А ).
2.3. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ, АКСИОМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Можно заметить, что при многократном повторении опыта со случайными исходами одни события происходят чаще, а другие - реже. Например, при многократном бросании игрального кубика четное число выпадет примерно в половине случаев, в то время как доля чисел кратных трем будет близка к одной трети.
Вероятность события
Для того чтобы сравнивать случайные события по степени возможности их наступления, следует с каждым из них связать какое-то число, которое тем больше, чем более возможно это событие. Это число определяет вероятность события.
Вероятность события - это количественная характеристика возможности его появления.
Вероятность обозначается буквой «Р»: например, вероятность события А обозначается как Р(А) или РА.
Свое первоначальное развитие теория вероятностей получила при анализе азартных игр и применялась к опытам, все исходы которых рав-новозможны.
Исходы опыта называют равновозможными, если нет объективных причин, в силу которых одни исходы должны появляться чаще других.
Например, вследствие симметрии игральной кости возможности выпадения всех ее граней одинаковы. Поэтому бросок игральной кости - опыт с равновозможными исходами.
Классическое определение вероятности
Рассмотрим опыт, имеющий N равновозможных исходов. Обозначим NA - число исходов, благоприятных для события А.
Вероятность случайного события - это отношение числа благоприятствующих ему исходов к числу всех равновозможных исходов данного опыта:
Ра = N/N. (2.1)
Исторически за этой формулой закрепилось название «Классическое определение вероятности». Это был первый количественный результат формирующейся теории, который позволил определять шансы на успех в различного рода азартных играх. Рассмотрим применение этого определения к игре в кости.
Задача. Игроки А и В играют, бросая по 2 кости. Игрок А выигрывает в том случае, когда сумма выпавших очков равна 7. Игрок В выигрывает в том случае, когда сумма выпавших очков равна 8. Кому выгодна эта игра?
Решение. Исходом каждого броска является выпадение пары граней. Вследствие симметрии костей все исходы равновозможны, а их количество N = 6 ? 6 = 36.
Выигрышу игрока А (событие А) благоприятствуют 6 исходов (1-6, 6-1, 2-5, 5-2, 3-4, 4-3); NA = 6. Выигрышу игрока В (событие В) благоприятствуют 5 исходов (2-6, 6-2, 5-3, 3-5, 4-4); NВ = 5. Используя формулу (2.1), найдем: Ра = 6/36, Рв = 5/36. Таким образом, игроку А игра выгоднее.
Аксиомы теории вероятностей
Далеко не все опыты имеют равновозможные исходы. Например, при стрельбе по мишени возможности попадания и промаха явно различны. Для того чтобы распространить понятие вероятности на произвольные опыты со случайными исходами, потребовалось введение ряда общих понятий и свойств.
Границы, в которых изменяется вероятность события, устанавливают по отношению к двум специальным понятиям.
1. Достоверным называется событие, которое в результате эксперимента должно произойти обязательно. Таким событием является множество всех возможных исходов Ω.
2. Невозможным называется событие, которое в данном опыте произойти не может. Например, при игре в рулетку не может выпасть число 38 - его просто нет на колесе. Невозможное событие обозначают символом Ǿ.
Вероятность достоверного события принимают за единицу:
Ρω = 1.
Вероятность невозможного события принимают за ноль:
Р(Ǿ) = 0.
К этим свойствам вероятности добавляют еще две аксиомы:
• вероятность любого события А лежит между нулем и единицей:
0 < Ра < 1;
• вероятность суммы несовместных событий равна сумме их вероятностей:
Р(А + В) = Ра + Рв. (2.2)
Можно доказать, что вероятность суммы совместных событий находится по следующей формуле:
Р(А + В) = Ра + Рв - Ρ (А ? В). (2.3)
2.4. ОТНОСИТЕЛЬНАЯ ЧАСТОТА СОБЫТИЯ, ЗАКОН БОЛЬШИХ ЧИСЕЛ
Условия, в которых допустимо использовать классическое определение вероятности, встречаются чрезвычайно редко, поскольку опыты с равновозможными исходами скорее исключение, чем правило. Если же исходы не являются равновозможными, то вероятность события нельзя вычислять по формуле (2.1).
Рассмотрим метод экспериментальной оценки вероятности некоторого события А. Выполним один и тот же опыт несколько раз и подсчитаем, в скольких опытах данное событие произошло.
Относительной частотой некоторого события А в выполненной серии опытов называют отношение числа опытов (иА), в которых событие произошло, к общему числу проведенных опытов (и):
При небольшом n относительная частота события носит в значительной степени случайный характер. Однако по мере увеличения числа проведенных опытов частота проявляет тенденцию стабилизироваться, приближаясь с незначительными колебаниями к некоторой постоянной величине. Ниже приводится таблица, в которой показано, как меняются частоты (Р*) выпадения герба при увеличении числа бросков (n) симметричной монеты.

Таблица 2.1

График, соответствующий этим изменениям, представлен на рис. 2.4.
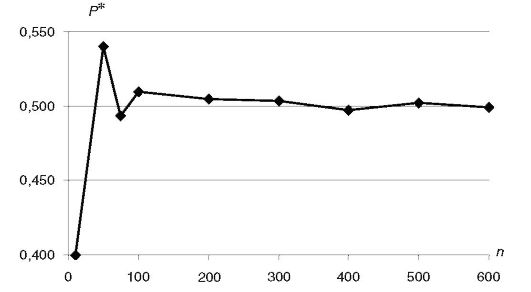
Рис. 2.4. Сходимость относительной частоты события к его вероятности
Относительная частота события и его вероятность связаны между собой законом больших чисел.
При неограниченном увеличении числа испытаний частота события стремится к его вероятности:
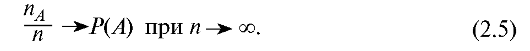
Это соотношение иногда называют статистическим определением вероятности. В соответствии с законом больших чисел, за вероятность события можно принять его относительную частоту при большом числе испытаний.
2.5. НЕЗАВИСИМЫЕ СОБЫТИЯ. СЛОЖЕНИЕ И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ НЕЗАВИСИМЫХ СОБЫТИЙ
Понятие статистической независимости занимает в теории вероятностей важное место и определяется следующим образом.
События А и В называются независимыми, если факт наступления одного из них не меняет вероятности наступления другого.
Типичный пример независимых событий - события, появляющиеся в опытах с независимыми исходами.
Два опыта называются независимыми, если исход одного опыта не может повлиять на исход другого опыта.
Например, при броске двух игральных кубиков результат первого броска никак не влияет на результат второго броска.
Для независимых событий выполняется теорема умножения вероятностей.
Вероятность события, которая является произведением независимых событий А и В, равна произведению их вероятностей:
Р(А ? В) = Ра ? Рв. (2.6)
Пример. Пусть в одной урне находятся 5 черных и 10 белых шаров, а в другой урне - 3 черных и 17 белых. Найти вероятность того, что при извлечении по одному шару из каждой урны оба шара окажутся черными.
Событие А - извлечение черного шара из первой урны:
Ра = 5/15 = 1/3 . Событие В - извлечение черного шара из второй урны:
Рв = 3/20.
Событие А ? В - оба шара имеют черный цвет:
Р(А ? В) = Ра ? Рв = 1/3 ? 3/20 = 1/20.
Применение теоремы умножения вероятностей к формуле (2.3) приводит к следующему закону нахождения вероятности суммы двух независимых событий:
Р(А + В) = Ра + Рв - Ра ? Рв. (2.7)
Пример. Пусть в одной урне находятся 5 черных и 10 белых шаров, а в другой урне - 3 черных и 17 белых. Найти вероятность того, что при извлечении по одному шару из каждой урны хотя бы один шар окажется черным. Используя значения Ра, Рв и Р(А ? В), полученные в предыдущем примере, найдем:
Р(А + В) = 1/3 + 3/20 - 1/20 = 22/60. 2.6. ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.
РЯД РАСПРЕДЕЛЕНИЯ, ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ.
ПЛОТНОСТЬ ВЕРОЯТНОСТИ
Часто с исходами опыта связывают числовые значения. Например, на гранях кубика написаны числа, поэтому выпадение какой-либо грани есть выпадение соответствующего числа. При повторных бросаниях кубика выпадающие числа будут меняться случайным образом. В этом случае говорят о случайной величине.
Под случайной величиной (СВ) понимается величина, значение которой зависит от исходов опыта со случайными исходами.
Случайные величины обозначают большими буквами (X, К..), а их значения - малыми буквами (x, y...).
Из множества всех случайных величин выделяют два наиболее часто встречающихся вида: дискретные и непрерывные.
Дискретная случайная величина - такая СВ, которая может принимать только конечное (или счетное) множество значений.
Эти значения нумеруются х1, х2, х3..., а вероятности их появления обозначаются p1, p2, p3...
Мы будем рассматривать дискретные величины с конечным множеством значений. Примерами таких величин являются число букв на случайно выбранной странице книги, энергия электрона в атоме, число зерен в колосе пшеницы и т.п.
Непрерывная случайная величина - такая СВ, которая может принимать любое значение в некотором определенном интервале (а, b).
Границы интервала могут принимать и бесконечно большие значения.
Примерами непрерывных случайных величин являются средняя температура воздуха в определенный промежуток времени, масса зерен в колосе пшеницы, результат любого количественного анализа в медицине и т.п.
Ряд распределения дискретной случайной величины
Дискретная случайная величина считается заданной, если известны ее возможные значения х1, x2...xNи соответствующие им вероятности p1, p2...pN. Совокупность значений СВ и их вероятностей, заданная в виде таблицы, называется рядом распределения, или распределением дискретной случайной величины:

Сумма всех вероятностей равна единице:

Ряд распределения является самой полной характеристикой дискретной СВ.
Функция распределения
Полной характеристикой непрерывной случайной величины является функция распределения F(x), значение которой в каждой точке х равно вероятности того, что случайная величина X примет значение, меньшее х:

Вероятность того, что значение СВ окажется меньше 1, равна 0 (все числа меньше +оо - достоверное событие), поэтому Д+оо) = 1. Вероятность того, что значение СВ окажется меньше -оо, равна нулю (нет таких чисел - невозможное событие), поэтому F(-о) = 0. Характерный вид функции распределения показан на рис. 2.5.
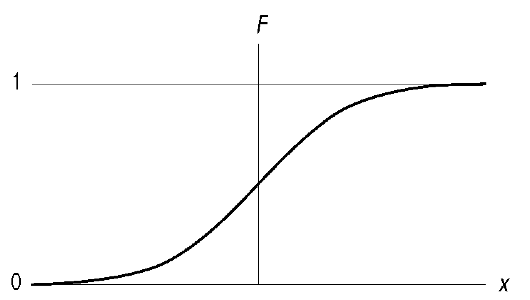
Рис. 2.5. Характерный вид функции распределения случайной величины
Функция распределения позволяет рассчитать вероятность того, что при выполнении опыта значение непрерывной случайной величины попадет в заданный интервал (х1, х2):
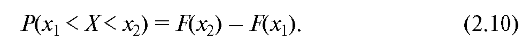
Плотность распределения
Функции распределения всех непрерывных случайных величин похожи друг на друга - все они монотонно возрастают от 0 до 1. Индивидуальные особенности случайных величин позволяет выявить другая функция, называемая плотностью распределения.
Плотностью распределения (или плотностью вероятности) f(x) непрерывной случайной величины называется производная от функции распределения:

Плотность распределения имеет следующее вероятностное истолкование.
Вероятность того, что непрерывная случайная величина X принимает значения из малого интервала (х, х+ ах), равна произведению плотности вероятности на ширину интервала:

Если нарисовать график плотности распределения, то вероятность того, что при выполнении опыта значение непрерывной случайной величины попадет в заданный интервал (х1, х2), равна площади соответствующей криволинейной трапеции (рис. 2.6). При этом площадь под всем графиком равна единице. Это условие эквивалентно условию нормировки (2.8) для дискретных СВ.
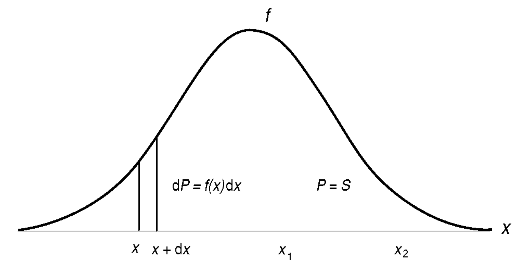
Рис 2.6. Характерный вид плотности распределения случайной величины
Для задач практической статистики интерес представляют только три вида интервалов: «левый хвост» распределения (-да, х1); «центральный» интервал (х1, х2) и «правый хвост» распределения (х2, +∞).
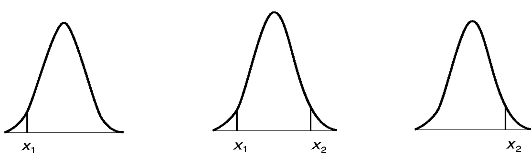
Рис. 2.7. Интервалы, используемые в практической статистике
2.7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Ряд распределений и плотность распределения несут полную информацию о соответствующей случайной величине, однако при решении многих практических вопросов достаточно знать две числовые характеристики случайной величины: математическое ожидание и дисперсию. Мы дадим не очень строгое, но понятное определение этих характеристик.
Математическое ожидание МХ случайной величины Х - это ее среднее арифметическое значение.
В это определение вкладывается следующий смысл. Пусть в серии из n опытов получены n значений случайной величины: х1, х2, ... хп. При неограниченном увеличении длины серии среднее арифметическое всех полученных значений стремится к МХ:

Возможные значения случайной величины рассеяны вокруг ее математического ожидания М(х): часть из них превышает М(х), часть - меньше М(х). Рассеяние значений случайной величины вокруг ее математического ожидания оценивают с помощью дисперсии.
Дисперсия - это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Формулы для расчета дисперсии дискретной и непрерывной случайных величин имеют следующий вид:
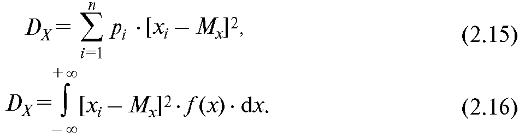
При вычислении дисперсии отклонения значения случайной величины возводятся в квадрат. Это делается для подавления знака минус, который появляется в тех случаях, когда х < МХ. Если этого не делать, то отрицательные и положительные значения скомпенсируют друг друга и в результате получится ноль. Для того чтобы избавиться от последствий возведения отклонений в квадрат, после вычисления дисперсии из нее извлекают квадратный корень. Полученную при этом величину используют в качестве меры отклонения случайной величины от среднего значения.
Среднеквадратическое отклонение (СКО) случайной величины - это квадратный корень из ее дисперсии:

(иногда употребляют термин «стандартное отклонение»).
При обработке данных над случайными величинами выполняют математические действия, в результате которых получаются новые случайные величины. Покажем, как меняются при этом математические ожидания и дисперсии.
1. При сложении случайной величины с константой (С) константа добавляется к математическому ожиданию, а дисперсия и СКО не меняются:
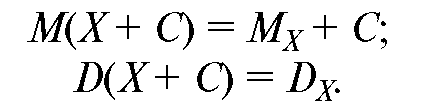
2. При умножении (делении) случайной величины на константу (k) математическое ожидание умножается на константу, а дисперсия на ее квадрат:
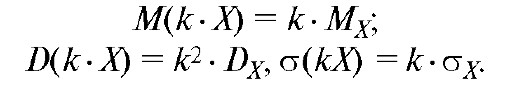
3. При сложении случайных величин (как независимых, так и зависимых) их математические ожидания складываются:
4. При сложении независимых случайных величин их дисперсии складываются:
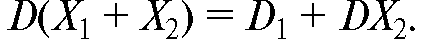
2.8. НЕКОТОРЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
Рассмотрим некоторые важные для практического использования законы распределения случайной величины.
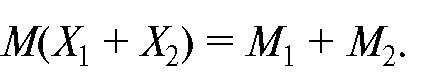
Нормальный закон распределения (закон Гаусса)
Случайная величина ^распределена по нормальному закону, если она определена на всей числовой оси и ее плотность вероятности определяется формулой:
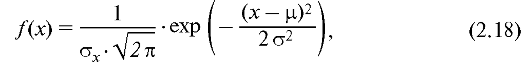
где μ = МХ - математическое ожидание случайной величины; σ - ее среднеквадратическое отклонение.
Важность нормального закона распределения для практической статистики связана с центральной предельной теоремой, согласно которой сумма большого числа независимых случайных величин с одинаковым законом распределения имеет распределение, которое можно считать нормальным. При этом закон распределения, которому подчиняются слагаемые, значения не имеет и может быть вообще не известен. Мы будем использовать это свойство в следующем параграфе.
На рис. 2.8 представлены графики плотности вероятности двух нормально распределенных СВ с μ = 0, σ = 2 и μ = 2, σ = 1. Отметим некоторые свойства этих графиков:
• график плотности распределения нормального закона имеет симметричный, колоколообразный вид; линия симметрии проходит через математическое ожидание случайной величины (х = μ);
• в точке х = μ функция достигает максимума;
• параметр σ характеризует форму кривой распределения: чем меньше σ, тем уже и выше график.
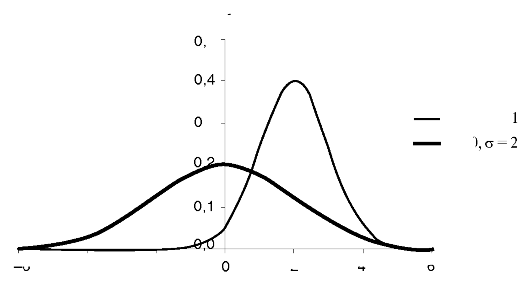
Рис. 2.8. Графики плотности вероятности нормального закона распределения
Для вычисления значений функции распределения и плотности вероятностей нормального закона используются компьютерные функции. В широко известном приложении Excel эти вычисления выполняет статистическая функция НОРМРАСП(х, μ, σ, m). При m = 0 вычисляется плотность распределения, а при m = 1 вычисляется функция распределения.
Нормальное распределение с μ = 0 и σ = 1 называется стандартным. Используя свойства математического ожидания и дисперсии, нетрудно показать, что если случайная величина Х имеет нормальное распределение с параметрами μ и σ, то случайная величина Х0 = (Х - μ)/σ имеет стандартное нормальное распределение. Отсюда получается, что вероятность события |Х - μ| < равна вероятности события |Х0| < к. Используя формулу (2.10), найдем
Р(-kσ <|Х - μ| < kσ) = НОРМРАСП(к, 0, 1, 1) - НОРМРАСП(-к, 0, 1, 1).
Для к = 1, к = 2 и к = 3 получим:
Р (-σ < X - a < σ ) = 0,6826,
Р (-2σ < X - a < 2σ) = 0,9544, (2.19)
Р (-3σ < X - a < 3σ) = 0,9974.
Последнее число показывает, что вероятность отклонения нормально распределенной случайной величины от среднего более чем на 3σ составляет всего 0,26%. Соотношения (2.19) показаны на рис. 2.9.
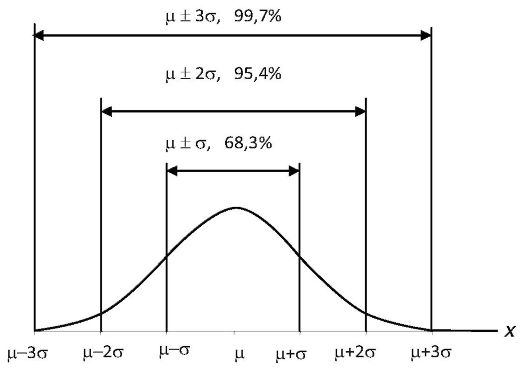
Рис. 2.9. Вероятности отклонения нормально распределенной случайной величины от математического ожидания
Распределение X2, распределение Стьюдента и распределение Фишера
Со стандартным нормальным распределением связаны еще три распределения, которые играют важную роль в математической статистике.
Распределение X2
Пусть Х1, Х2, ... Ху - независимые случайные величины, имеющие стандартное нормальное распределение. Тогда сумма их квадратов подчиняется распределению χ2 (хи-квадрат):
Y = Х2 + Х22 +... + Ху2. (2.20)
Число слагаемых ν (ню) называют числом степеней свободы. График плотности распределения для ν = 5 представлен на рис. 2.10.
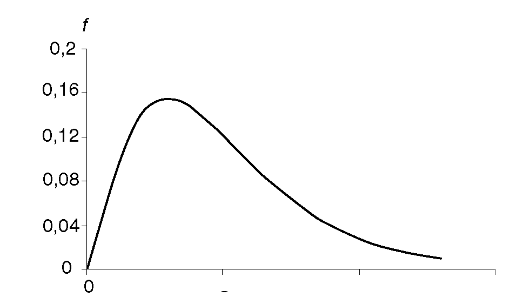
Рис. 2.10. Плотность распределения χ2 для ν = 5
Распределение Стьюдента
Если х случайная величина со стандартным нормальным распределением, а y - имеет распределение χ2 с числом степеней свободы ν, то случайная величина

подчиняется распределению Стьюдента с ν степенями свободы. График плотности распределения Стьюдента похож на график стандартного нормального распределения и здесь не приводится.
Распределение Фишера
Если y1иy2 - независимые случайные величины, имеющие χ2^^ пределение с ν1 и ν2 степенями свободы соответственно, то отношение

имеет F-распределение Фишера. При этом ν1 называют числом степеней свободы числителя, а ν2 - числом степеней свободы знаменателя.
График плотности F-распределения для ν1 = 5 и ν2 = 10 представлен на рис. 2.11.
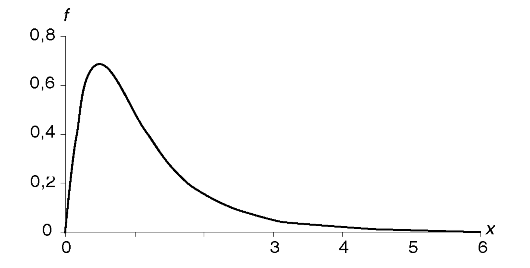
Рис. 2.11. Плотность /-распределения для ν = 5 и ν2 = 10
Экспоненциальный закон распределения. Распределение Больцмана
Непрерывная случайная величина c положительными значениями, плотность вероятности которой задана формулой:
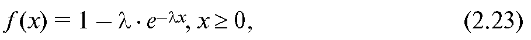
называется распределенной по экспоненциальному закону.
Функция распределения экспоненциального закона выражается формулой:

В физике вместо функции распределения (2.21) используют функцию:

которая равна вероятности того, что СВ примет значение, большее х. С помощью этой функции описывают распределение частиц по потенциальным энергиям в силовых полях. Такое распределение называют распределением Больцмана. Из статистического распределения Больцма-на вытекает, например, барометрическая формула, определяющая распределение по высоте газа в поле тяжести Земли:

где n и n0 - концентрации молекул на высоте h и у поверхности Земли; m - масса молекулы; k - постоянная Больцмана; Т - абсолютная температура.