Глава 28. Волновые свойства частиц. Элементы квантовой механики

Квантовой механикой называют современную теорию, устанавливающую способ описания и законы движения микрочастиц (элементарных частиц, атомов, молекул, ядер) и их систем. Необычность квантово-механических представлений по сравнению с классической физикой открыла период ломки основных физических моделей, которые казались очевидными и нерушимыми. Главным образом это коснулось понятия частицы и принципов ее движения.

В этой главе дается понятие не только о квантовой механике, но и о тех идеях и опытах, которые привели к этой теории. Как метод, основанный на волновых свойствах электронов, рассматривается электронная микроскопия.

28.1. ГИПОТЕЗА ДЕ БРОЙЛЯ. ОПЫТЫ ПО ДИФРАКЦИИ ЭЛЕКТРОНОВ И ДРУГИХ ЧАСТИЦ

Важным этапом в создании квантовой механики явилось обнаружение волновых свойств микрочастиц. Идея о волновых свойствах была первоначально высказана как гипотеза французским физиком Луи де Бройлем (1924)¹.

В физике в течение многих лет господствовала теория, согласно которой свет есть электромагнитная волна. Однако после работ Планка (тепловое излучение), Эйнштейна (фотоэффект) и других стало очевидным, что свет обладает корпускулярными свойствами.

¹ Гипотеза де Бройля была сформулирована до опытов, подтверждающих волновые свойства частиц. Де Бройль об этом позднее, в 1936 г. писал так: «... не можем ли мы предположить, что и электрон так же двойственен, как и свет? На первый взгляд такая идея казалась очень дерзкой. Ведь мы всегда представляли себе электрон в виде электрически заряженной материальной точки, которая подчиняется законам классической динамики. Электрон никогда явно не проявлял волновых свойств, таких, скажем, какие проявляет свет в явлениях интерференции и дифракции. Попытка приписать волновые свойства электрону, когда этому нет никаких экспериментальных доказательств, могла выглядеть как ненаучная фантазия».

В гл. 24 было отмечено, что дифракция рентгеновских лучей наблюдается на кристаллических телах; следовательно, для дифракции электронов необходимо также использовать кристаллические вещества.

К. Дэвиссон и Л. Джермер впервые наблюдали дифракцию электронов на монокристалле никеля, Дж.П. Томсон и независимо от него П.С. Тартаков-ский - на металлической фольге (по-ликристаллиаеское тело).

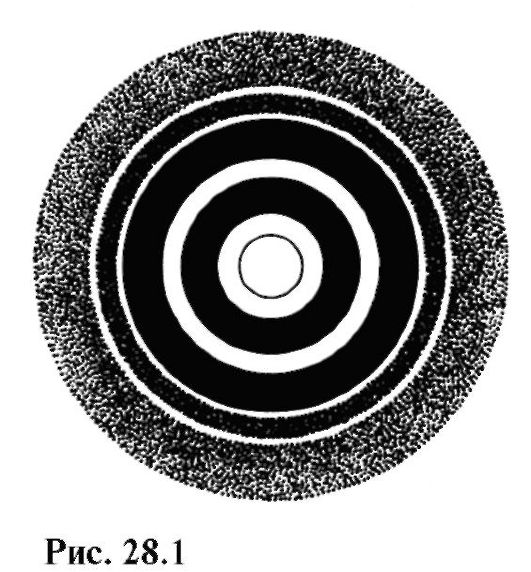
На рис. 28.1 изображена электроно-грамма - дифракционная картина, полученная от взаимодействия электронов с поликристаллической фольгой.

Сравнивая этот рисунок с рис. 24.21, можно заметить сходство дифракции электронов и рентгеновских лучей.

Способностью дифрагировать обладают и другие частицы, как заряженные (протоны, ионы и др.), так и нейтральные (нейтроны, атомы, молекулы).

Аналогично рентгеноструктурному анализу можно применять дифракцию частиц для определения упорядоченного или разупорядочен-ного расположения атомов и молекул вещества и для оценки параметров кристаллических решеток.

В настоящее время широкое распространение имеют методы электронографии (дифракция электронов) и нейтронографии (дифракция нейтронов).

Могут возникнуть вопросы: что происходит с отдельными частицами, как образуются максимумы и минимумы при дифракции отдельных частиц?

Опыты по дифракции пучков электронов очень малой интенсивности, т.е. как бы отдельных частиц, показали, что при этом электрон не «размазывается» по разным направлениям, а ведет себя как целая частица. Однако вероятность отклонения электрона по отдельным направлениям в результате взаимодействия с объектом дифракции различная. Наиболее вероятно попадание электронов в те места, которые по расчету соответствуют максимумам дифракции, менее вероятно их попадание в места минимумов. Таким образом, волновые свойства присущи не только коллективу электронов, но и каждому электрону в отдельности.

28.2. ЭЛЕКТРОННЫЙ МИКРОСКОП. ПОНЯТИЕ ОБ ЭЛЕКТРОННОЙ ОПТИКЕ

Волновые свойства частиц можно использовать не только для дифракционного структурного анализа, но и для получения увеличенных изображений предмета.

Из (26.19) следует, что предел разрешения оптического микроскопа в основном определяется предельным значением длины волны света, воспринимаемого глазом человека. Подставив в эту формулу значение длины волны де Бройля (28.3), найдем предел разрешения электронного микроскопа, в котором изображение предмета формируется электронными пучками:

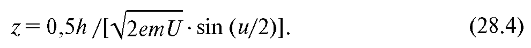
Как нетрудно убедиться, предел разрешения z электронного микроскопа зависит от ускоряющего напряжения, и можно добиться, чтобы он был значительно меньше, а разрешающая способность значительно больше, чем у оптического микроскопа.

Электронный микроскоп и его отдельные элементы по своему назначению подобны оптическому, поэтому воспользуемся аналогией для объяснения его устройства и принципа действия. Схемы обоих микроскопов изображены на рис. 28.2 (а - оптический; б - электронный).

В оптическом микроскопе носителем информации о предмете АВ является фотон, свет. Источником света обычно служит лампа накаливания /. После взаимодействия с предметом (поглощение, рассеяние, дифракция) поток фотонов преобразуется и содержит информацию о предмете. Поток фотонов формируется с помощью оптических устройств, в основном линз: конденсора 3, объектива 4, окуляра 5. Изображение А₁В₁ регистрируется глазом 7 (или фотопластинкой, фотолю-минесцирующим экраном и т.д.).

В электронном микроскопе носителем информации о предмете является электрон, а источником электронов - подогреваемый катод 1. Ускорение электронов и образование пучка осуществляют фокусирующим электродом и анодом - системой, называемой электронной пушкой 2. После взаимодействия с предметом (в основном рассеяние) поток электронов преобразуется и содержит информацию о предмете. Формирование потока электронов происходит под воздействием электрического поля (система электродов и конденсаторов) и магнитного (систе-

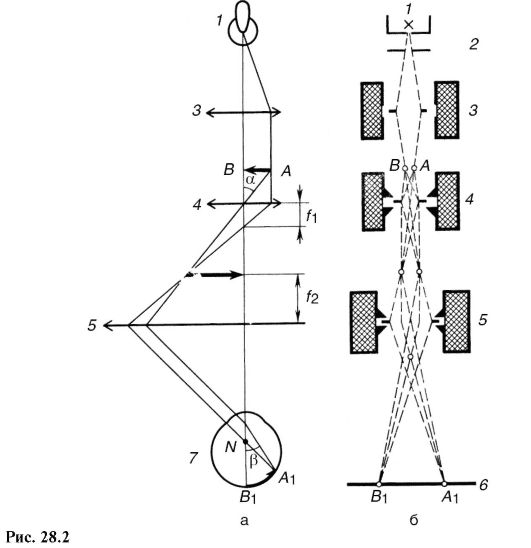
ма катушек с током). Эти системы называют электронными линзами по аналогии с оптическими линзами, которые формируют световой поток (3 - конденсорная; 4 - электронная, служащая объективом, 5 - проекционная). Изображение регистрируется на чувствительной к электронам фотопластинке или катодолюминесцирующем экране 6.

Чтобы оценить предел разрешения электронного микроскопа, подставим в формулу (28.4) ускоряющее напряжение 100 кВ и угловую апертуру порядка 10^-2 рад (приблизительно такие углы используют в электронной микроскопии). Тогда получим z ~ 0,1 нм, что в сотни раз лучше, чем у оптических микроскопов. Применение ускоряющего напряжения, большего 100 кВ, хотя и повышает разрешающую способность, но связано с некоторыми сложностями, в частности происходит

разрушение исследуемого объекта электронами, имеющими большую скорость. Практически даже с помощью самого хорошего электронного микроскопа можно достичь предела разрешения порядка 10^-10 м; это в сотни раз лучше, чем у оптических микроскопов.

К достоинствам электронного микроскопа следует отнести большую разрешающую способность, позволяющую рассматривать крупные молекулы, возможность изменять при необходимости ускоряющее напряжение и, следовательно, предел разрешения и сравнительно удобное управление потоком электронов с помощью магнитных и электрических полей.

Укажем некоторые особенности эксплуатации электронного микроскопа. В тех частях его, где пролетают электроны, должен быть вакуум, так как в противном случае столкновение электронов с молекулами воздуха (газа) приведет к искажению изображения. Это требование к электронной микроскопии усложняет процедуру исследования, делает аппаратуру более громоздкой и дорогой. Вакуум искажает нативные свойства биологических объектов, а в ряде случаев разрушает или деформирует их.

Для рассматривания в электронном микроскопе пригодны лишь очень тонкие срезы, так как электроны сильно поглощаются и рассеиваются веществом. Поэтому в некоторых случаях целесообразно сделать оттиск исследуемой поверхности объекта на тонком слое пластмассы. Эту процедуру называют репликацией, а пластмассовую копию поверхности - репликой.

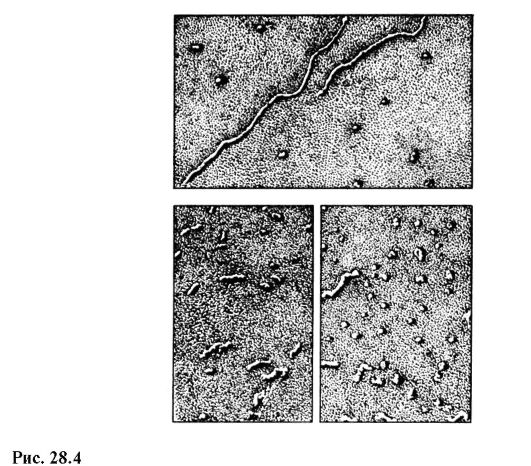
Современный отечественный электронный микроскоп ЭВМ-100 ЛМ (рис. 28.3) дает максимальное 600 000-кратное увеличение и гарантированный предел разрешения 3 ? 10^-10 м. На рис. 28.4 приведены снимки молекул РНК в разных состояниях, полученные на электронном микроскопе с увеличением в 100 000 раз.

Наличие волновых и корпускулярных свойств как у фотонов, так и у электронов и других частиц позволяет ряд положений и законов оптики распространить и на описание движения заряженных частиц в электрических и магнитных полях.

Эта аналогия позволила выделить как самостоятельный раздел электронную оптику - область физики, в которой изучается структура пучков заряженных частиц, взаимодействующих с электрическими и магнитными полями. Как и обычную оптику, электронную можно подразделить на геометрическую (лучевую) и волновую (физическую).

В рамках геометрической электронной оптики, в частности, описывается движение заряженных частиц в электрическом и магнитном полях. Схематическое изображение построения изображения в электронном микроскопе (см. рис. 28.2, б) основывается на геометрической электронной оптике.

Подход волновой электронной оптики существен в том случае, когда проявляются волновые свойства заряженных частиц. Хорошей иллюстрацией является нахождение разрешающей способности (предела разрешения), приведенное в начале параграфа.

28.3. ВОЛНОВАЯ ФУНКЦИЯ И ЕЕ ФИЗИЧЕСКИЙ СМЫСЛ

Так как с микрочастицей сопоставляют волновой процесс, который соответствует ее движению, то состояние частиц в квантовой механике описывается волновой функцией, зависящей от координат и времени: ψ(χ, у, z, t).

Если силовое поле, действующее на частицу, является стационарным, т.е. не зависящим от времени, то ψ-функцию можно представить в виде произведения двух сомножителей, один из которых зависит от времени, а другой - от координат:

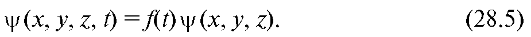
В дальнейшем будем рассматривать только стационарные состояния; ψ-функция является вероятностной характеристикой состояния частицы. Поясним смысл этого утверждения.

Выделим в пространстве достаточно малый объем dV = dxdjdz, в пределах которого значения ψ-функции можно считать одинаковыми. Вероятность нахождения dW_B частицы в этом объеме пропорциональна объему и зависит от квадрата модуля ψ-функции:

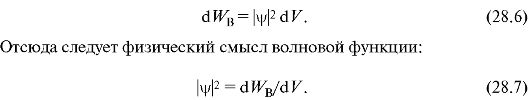
Квадрат модуля волновой функции равен плотности вероятности, т.е. отношению вероятности нахождения частицы в объеме к этому объему.

Интегрируя выражение (28.6) по некоторому объему V, находим вероятность нахождения частицы в этом объеме:

28.4. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ

Одним из важных положений квантовой механики являются соотношения неопределенностей, предложенные В.Гейзенбергом.

Пусть одновременно измеряют положение и импульс частицы, при этом неточности в определениях абсциссы и проекции импульса на ось абсцисс равны соответственно Δχ и Δр_х.

¹ Реально осуществить такой опыт невозможно, так как размеры щели должны быть порядка атомов, поэтому описывается некоторый мысленный эксперимент.

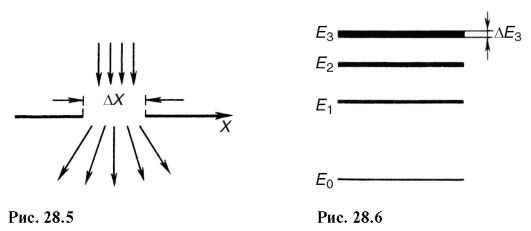
шение (28.11) означает, что чем меньше время существования какого-либо состояния системы, тем более неопределенно его значение энергии. Энергетические уровни Е₁, Е₂ и т.д. имеют некоторую ширину (рис. 28.6), зависящую от времени пребывания системы в состоянии, соответствующем этому уровню.

«Размытость» уровней приводит к неопределенности энергии АЕ излучаемого фотона и его частоты Ау при переходе системы с одного энергетического уровня на другой:

Так как состояние микрочастицы описывают ψ-функцией, то надо указать способ нахождения этой функции с учетом внешних условий. Это возможно в результате решения основного уравнения квантовой механики, предложенного Э. Шредингером (1926). Такое уравнение в квантовой механике постулируется так же, как в классической механике постулируется второй закон Ньютона.

Применительно к стационарным состояниям уравнение Шредин-гера может быть записано так:

Это проявляется в уширении спектральных линий.

28.5. УРАВНЕНИЕ ШРЕДИНГЕРА. ЭЛЕКТРОН В ПОТЕНЦИАЛЬНОЙ ЯМЕ

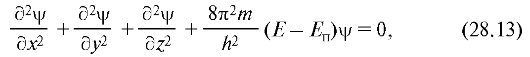
где m - масса частицы; Е и Е_п - ее полная и потенциальная энергии (потенциальная энергия определяется силовым полем, в котором находится частица, и для стационарного случая не зависит от времени).

Если частица перемещается только вдоль некоторой линии, например вдоль оси Х (одномерный случай), то уравнение Шредингера существенно упрощается и принимает вид:

Одним из наиболее простых примеров на использование уравнения Шредингера является решение задачи о движении частицы в одномерной потенциальной яме.

Пусть электрон перемещается вдоль оси Х только в пределах 0 < х < l (рис. 28.7). Это означает, что в указанном интервале ψ-функция отлична от нуля, а вне интервала (х <0, х >l) равна нулю.

Так как на частицу в выделенном интервале силовые поля не действуют, то ее потенциальная энергия может иметь любое постоянное значение (наиболее удобно принять Е_п = 0). Вне этого интервала электрона нет, поэтому следует считать его потенциальную энергию бесконечно большой. На рис. 28.7 показана графическая зависимость Е_п = Дх). Интервал 0 < х < l, удовлетворяющий сформулированным выше условиям, называют одномерной прямоугольной потенциальной ямой с бесконечно высокими стенками. С учетом Е_п = 0 уравнение Шредингера (28.14) для интервала 0 < х < l имеет вид:

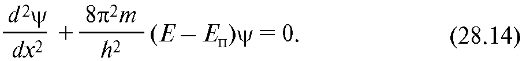
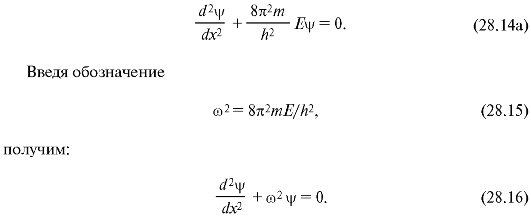
Это уравнение аналогично дифференциальному уравнению гармонического колебания (см. 7.1), решение которого:

Прежде всего примечательно, что решение уравнения Шрединге-ра для электрона в потенциальной яме без каких-либо дополнительных постулатов приводит к дискретным, квантованным значениям энергии:

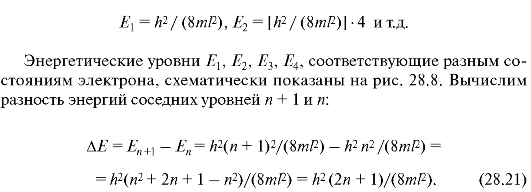
Из (28.21) видно, что при некотором фиксированном значении n дискретность, т.е. различие энергий соседних уровней, тем меньше, чем больше размеры потенциальной ямы. Так, например, рассчитаем два случая при n = 1:

1) l = 5 ? 10^-10 м, что примерно соответствует размерам атома; тогда ΔΕ = 4,5 эВ. Это по порядку величины совпадает со значениями, полученными для атома водорода по теории Бора;

2) l = 10^-1 м, что фактически соответствует такой ширине потенциальной ямы, что электрон можно считать свободным; при этом ΔΕ = 1,1 ? 10^-16 эВ. Здесь дискретность ничтожна и практически можно считать, что энергия электрона изменяется непрерывно.

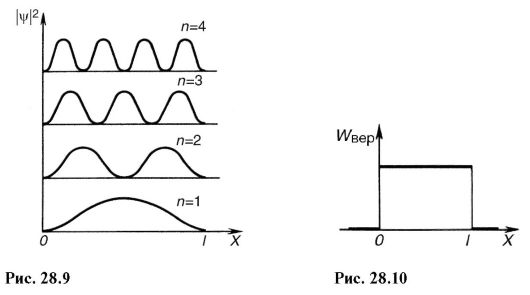
Возведя (28.20) в квадрат, получим плотность вероятности |ψ|² нахождения электрона в разных точках потенциальной ямы. На рис. 28.9 показана графическая зависимость |ψ|² от χ при разных дискретных состояниях, т.е. разных квантовых числах. Как видно из рисунка, электрон может с разной вероятностью находиться в различных местах потенциальной ямы. Есть такие точки, в которых вероятность нахождения электрона вообще равна нулю. Это существенно отличается от представлений классической физики, согласно которым равновероятно нахождение частицы в разных местах потенциальной ямы (рис. 28.10) и невозможно разделение ямы точками, в которых исключено нахождение частицы.

Уравнение Шредингера можно применить и к более сложным силовым полям, например к электрону в атоме. Это приведет к дополнительным математическим трудностям, но не изменит основных особенностей

атомных систем: дискретности энергетических состояний, вероятностных суждений о нахождении электрона, своеобразной зависимости |ψ|² от координат и т.д.

28.6. ПРИМЕНЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА К АТОМУ ВОДОРОДА. КВАНТОВЫЕ ЧИСЛА

Описание состояний атомов и молекул с помощью уравнения Шре-дингера является достаточно сложной задачей. Наиболее просто она решается для одного электрона, находящегося в поле ядра. Такие системы соответствуют атому водорода и водородоподобным ионам (однократно ионизированный атом гелия, двукратно ионизированный атом лития и т.п.). Однако и в этом случае решение задачи выходит за рамки нашего курса, поэтому ограничимся лишь качественным изложением вопроса.

Прежде всего в уравнение Шредингера (28.13) следует подставить потенциальную энергию, которая для двух взаимодействующих точечных зарядов - е (электрон) и Ze (ядро), - находящихся на расстоянии r в вакууме, выражается следующим образом:

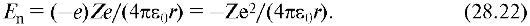
При центральной симметрии поля, созданного ядром, удобнее решать задачу не в декартовых прямоугольных координатах, а в сферических r, θ и р.

Решение уравнения Шредингера находят в виде произведения трех функций, каждая из которых зависит от одной переменной:

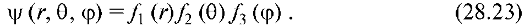
Аналогично тому, как для электрона в прямоугольной потенциальной яме с бесконечно высокими стенками граничные условия привели к конкретным возможным значениям ψ и энергии, так и в потенциальной яме, соответствующей атому водорода, физические условия приводят к возможным значениям f1, f₂, f₃ и, следовательно, ψ-функции. Здесь также проявляется главная особенность квантово-механических систем - дискретность состояний.

Дискретность математически заключается в том, что любая из функций уравнения (28.23) имеет целый набор (спектр) решений, каждому из которых отвечает определенное квантовое число. В отличие от прямоугольной потенциальной ямы с бесконечно высокими стенками состояние электрона в атоме характеризуется не одним, а несколькими квантовыми числа-ми¹. Первое из них - главное квантовое число п - 1, 2, 3... Оно определяет уровни энергии электрона по закону:

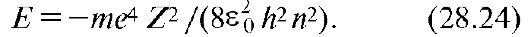
Это выражение является решением уравнения Шредингера и полностью совпадает с соответствующей формулой теории Бора (см. 28.7).

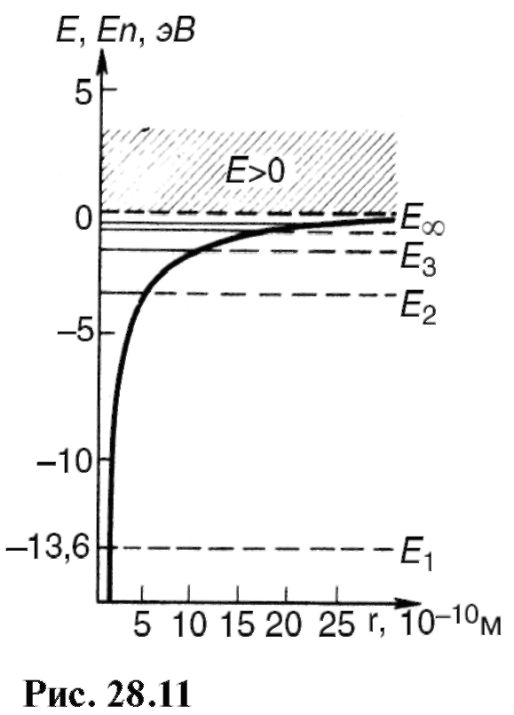
На рис. 28.11 показаны уровни возможных значений полной энергии атома водорода (Е₁, Е₂, Е₃ и т.д.) и график зависимости потенциальной энергии Е_П от расстояния r между электроном и ядром [см. (28.22)]. С возрастанием главного квантового числа п увеличивается r [см., например, (28.33)], а полная [см. (28.24)] и потенциальная энергии стремятся к нулю. Кинетическая энергия также стремится к нулю. Заштрихованная область (Е >0) соответствует состоянию свободного электрона.

¹ В общем случае квантовыми числами называют целые (0, 1, 2...) или полуцелые (1/2, 3/2, 5/2...) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы и элементарные частицы.

¹ Наличие спина у частиц не следует из уравнения Шредингера.

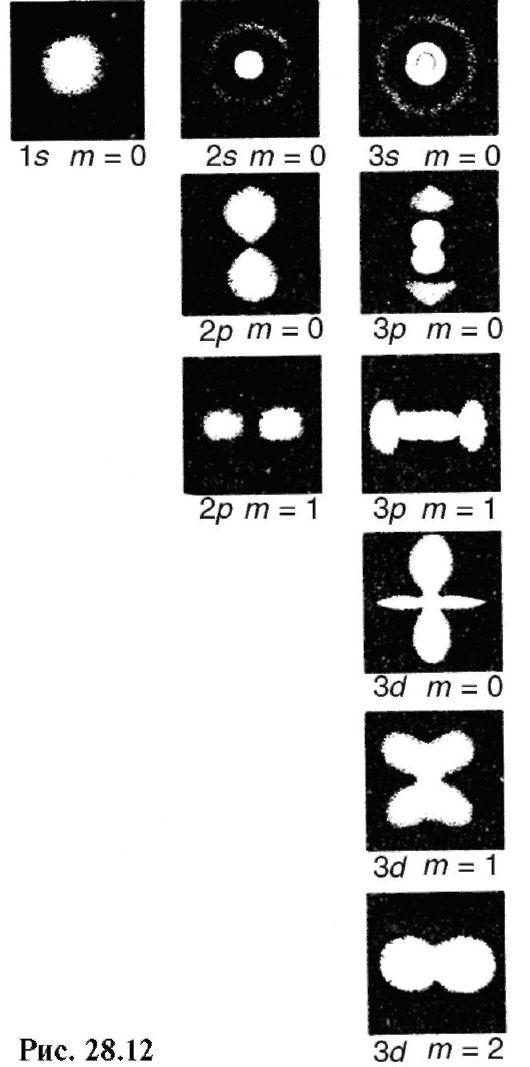
с этим расчетом: больше времени она находилась в местах с большей плотностью вероятности, менее длительно - в местах с меньшей плотностью вероятности. В результате экспозиции на фотопленке получились места разной интенсивности, которые иллюстрируют распределение электрона в атоме. Из рисунков видно, сколь условно и даже неверно понятие «орбита» применительно к движению электрона.

Спиновый и орбитальный магнитные моменты взаимодействуют между собой, это изменяет систему энергетических уровней атома по сравнению с той, которая была бы без такого взаимодействия. Говорят, что спин-орбитальное взаимодействие приводит к тонкой структуре энергетических уровней. Если оно существенно, то необходимо учитывать полный момент импульса электрона - орбитальный плюс спиновый. При этом вместо m_l и m_s используют другие квантовые числа: j и nij.

Квантовое число j - орбитальное плюс спиновое - определяет дискретные значения полного момента импульса L электрона:

Магнитное квантовое число m_} характеризует возможные проекции полного момента импульса на некоторое произвольно выбранное направление Z:

При заданном l квантовое число j принимает два значения: ±1/2

(табл. 28.1).

Таблица 28.1

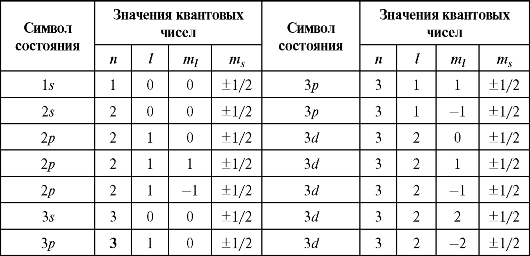
При заданном j квантовое число nij принимает 2j + 1 значений: -j, -j + 1 ... + j.

28.7. ПОНЯТИЕ О ТЕОРИИ БОРА

Еще до создания квантовой механики в 1913 г. датский физик Н. Бор предложил теорию атома водорода и водородоподобных ионов, которая основывалась на ядерной модели атома и двух его постулатах. Постулаты Бора не укладывались в рамки классической физики.

Согласно первому постулату, атом и атомные системы могут длительно пребывать только в некоторых стационарных состояниях. Находясь в таких состояниях, атом не излучает и не поглощает энергии. Стационарным состояниям соответствуют дискретные значения энергии: Е₁, Е₂...

Любое изменение энергии атома или атомной системы связано со скачкообразным переходом из одного стационарного состояния в другое.

По второму постулату, при переходе атома из одного состояния в другое атом испускает или поглощает фотон, энергия которого определяется уравнением (29.1).

Переход от состояния с большей энергией в состояние с меньшей энергией сопровождается излучением фотона. Обратный процесс возможен при поглощении фотона.

Согласно теории Бора, электрон в атоме водорода вращается по круговой орбите вокруг ядра. Из всех возможных орбит стационарные состояния соответствуют только тем, для которых момент импульса равен целому числу h/(2π):

(n = 1, 2, 3...), (28.31)

где m - масса электрона; υ_η - его скорость на n-й орбите; rn - ее радиус. На электрон, вращающийся по круговой орбите в атоме, действует куло-новская сила притяжения со стороны положительно заряженного ядра, которая, по второму закону Ньютона, равна произведению массы электрона на центростремительное ускорение (запись дана для вакуума):

Несмотря на большой успех теории Бора, скоро стали заметны и ее недостатки. Так, в рамках этой теории не удалось объяснить различие интенсивностей спектральных линий, т.е. ответить на вопрос, почему одни энергетические переходы более вероятны, чем другие. Теория Бора не раскрыла спектральных закономерностей более сложной атомной системы - атома гелия (два электрона, вращающиеся вокруг ядра).

Недостатком теории Бора была ее непоследовательность. Эта теория не была ни классической, ни квантовой, она объединяла в себе положения принципиально отличных теорий: классической и квантовой физики. Так, например, в теории Бора считается, что электрон вращается в атоме по определенной орбите (классические представления), но при этом он не излучает электромагнитной волны (квантовые представления).

В первой четверти нашего века стало ясно, что теория Бора должна быть заменена другой теорией атома. Появилась квантовая механика.

28.8. ЭЛЕКТРОННЫЕ ОБОЛОЧКИ СЛОЖНЫХ АТОМОВ

Квантовые числа, описывающие состояние электрона в атоме водорода, используют для приближенной характеристики состояния отдельных электронов сложных атомов. Однако при этом следует учитывать по крайней мере два существенных отличия сложных атомов от атома водорода:

1) в сложных атомах энергия электронов из-за их взаимодействия зависит не только от n, но и от /;

2) отличие обусловлено принципом Паули, согласно которому в атоме не может быть двух (и более) электронов с четырьмя одинаковыми квантовыми числами.

При образовании электронной конфигурации, соответствующей нормальному состоянию, каждый электрон атома стремится иметь наименьшую энергию. Если бы не принцип Паули, то все электроны расположились бы на самом нижнем энергетическом уровне. Фактически же, за некоторыми исключениями, электроны занимают ту последовательность состояний, которая указана для атома водорода в табл. 29.

Электроны с одинаковым главным квантовым числом образуют слой. Слои называются К, L, М, N и т.д. в соответствии с n = 1, 2, 3, 4... Электроны, имеющие одинаковые пары значений n и /, входят в состав оболочки, которая кратко обозначается так же, как соответствующие состояния для электрона атома водорода: 1s, 2s, 2^ и т.д. Так, например, называют 2s-оболочка, 2s-электроны и т.п.

Число электронов в оболочке обозначают справа вверху около символической записи оболочки, например 2р⁴.

Распределение электронов по оболочкам в атоме (электронные конфигурации) обычно указывают следующим образом: для азота 1s², 2s², 2р³, для кальция 1s², 2s², 2р⁶, 3s², 3р⁶, 4s² и т.д.

Так как энергия электронов сложных атомов зависит не только от n, но и от l, то построение таблицы Менделеева не всегда происходит постепенным заполнением слоев по мере усложнения атома. У калия (Z = 19), например, вместо заполнения слоя М (возможно, было 1s², 2s², 2^ ⁶, 3s², 3р ⁶, 3а¹) начинается заполнение слоя N и создается следующая электронная конфигурация: 1 s², 2s², 2р 6, 3s2, 3р 6, 4s1.

Аналогичные отклонения от регулярного заполнения слоев имеются и у других элементов.

Всегда выполняется общее правило: электроны невозбужденного атома занимают состояние с наименьшей энергией и в соответствии с принципом Паули. На рис. 28.13 схематически без соблюдения масштаба показаны энергетические состояния сложного атома и соответствующее им число электронов.

В заключение отметим, что состояние многоэлектронного атома в целом определяется следующими квантовыми числами: L - полного орбитального момента атома, которое принимает значения 0, 1, 2, 3 и т.д.¹; J - полного момента атома, которое может принимать значения с интервалом в единицу от |L - S | до |L + S |; S - результирующего спинового момента атома; магнитного m_J, который определяет дискретные значения проекции полного момента атома на некоторую ось Z:

При заданном Jm_J принимает 2J + 1 значений:

-J, -J + 1 ... +J.

¹ Не следует смешивать это обозначение с названием электронного слоя L и с полным моментом импульса электрона.

28.9. ЭНЕРГЕТИЧЕСКИЕ УРОВНИ МОЛЕКУЛ

Так как молекулы состоят из атомов, то внутримолекулярное движение сложнее внутриатомного. В молекуле кроме движения электронов относительно ядер происходит колебательное движение атомов около их положения равновесия (колебание ядер вместе с окружающими их электронами) и вращательное движение молекулы как целого.

Электронному, колебательному и вращательному движениям молекулы соответствуют три типа уровней энергии: Е_эл, Е_кол и Е_вр. Согласно квантовой механике, энергия всех видов движения в молекуле принимает только дискретные значения (квантуется). Представим приближенно полную энергию Е молекулы суммой квантованных значений энергий разных видов:

Е = Еэл + Екол + Евр^. (28.37)

На рис. 28.14 схематически изображена система уровней молекулы: далеко отстоящие электронные уровни энергии а' и а'', для которых Е_кол = Е_вр = 0; более близко расположенные колебательные уровни v', v'', для них Е_вр = 0; наиболее тесно расположенные вращательные уровни J' и J'' с различными значениями Е_вр.

Расстояние между электронными уровнями энергии порядка нескольких электрон-вольт, между соседними колебательными уровнями 10^-2-10^-1 эВ, между соседними вращательными уровнями 10^-5-10^-3 эВ.