Глава 26. Геометрическая оптика

Геометрическая (лучевая) оптика - раздел, в котором изучают законы распространения света на основании представления о световом луче как линии, вдоль которой распространяется энергия световой волны.

В главе законы геометрической оптики применяются к рассмотрению конкретных оптических систем. Наряду с этим излагаются вопросы физики глаза.

26.1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА КАК ПРЕДЕЛЬНЫЙ СЛУЧАЙ

ВОЛНОВОЙ ОПТИКИ

В предыдущих главах были рассмотрены явления, вполне удовлетворительно описываемые в рамках волновой природы света. Однако во многих практических вопросах, таких, как формирование светового пучка, образование изображения и др., волновая природа света может оказаться несущественной. Более того, учет интерференции, дифракции и поляризации в этих случаях лишь усложнит получение конечного результата. Для решения такого рода задач применяют законы геометрической оптики.

Геометрическая оптика есть предельный случай волновой оптики при стремлении длины волны к нулю.

Это можно пояснить на примере дифракционной решетки. Из (24.26) при λ -- 0 следует α -- 0, т.е. получаем обычное для линзы фокусирование параллельного пучка света в точке о фокальной плоскости

(см. рис. 24.10).

Для выяснения предельных возможностей оптических систем вновь приходится учитывать волновой характер света. Поэтому в этой главе частично рассматриваются вопросы интерференции и дифракции.

Геометрическая оптика является примером теории, позволившей при небольшом числе основных понятий и законов получить много практически важных результатов. В теории оптических устройств она и сейчас имеет большое значение.

26.2. АБЕРРАЦИИ ЛИНЗ

В данном курсе рассматриваются только сферические линзы, поверхностями которых являются выпуклые или вогнутые сферы. Фокусное расстояние такой линзы определяется формулой:

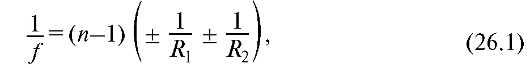
где R₁ и R₂ - радиусы кривизны передней и задней сферических поверхностей линзы соответственно; знак «+» берется для выпуклой поверхности, а знак «-» - для вогнутой; n - показатель преломления вещества, из которого изготовлена линза; окружающая среда - воздух. Фокусное расстояние двояковыпуклой линзы:

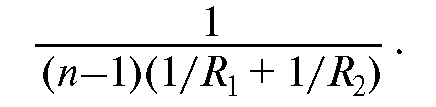
Величина обратная фокусному расстоянию линзы называется оптической силой D:

Приведем формулу тонкой линзы, известную из школьного курса:

где а₁ - расстояние от предмета до линзы; a₂ - расстояние от изображения до линзы.

Соотношение (26.1) получено для тонкой линзы при следующих предположениях:

1) изображение формируется приосевыми (параксиальньми) лучами;

2) лучи составляют небольшие углы с главной осью системы;

3) показатель преломления для всех длин волн одинаков.

При выполнении таких условий создается точечное изображение, т.е. каждая точка предмета дает одну точку изображения.

Эти условия не реализуются на практике. Показатель преломления зависит от длины волны (дисперсия).

Точки предмета лежат в стороне от оптической оси, что не отвечает второму условию. Применение только параксиальных лучей существенно ограничило бы световые потоки.

Все это приводит к аберрациям¹, или погрешностям реальных оптических систем, существенно снижающим качество оптических изобра-

¹ Aberratio (лат.) - уклонение.

жений. Однако, зная причины аберраций, можно добиться их устранения, если соответствующим образом подобрать систему линз. Рассмотрим некоторые основные аберрации линзы.

Сферическая аберрация

Она заключается в том, что периферические части линзы сильнее отклоняют лучи, идущие от точки S на оси, чем центральные (рис. 26.1). Изображение светящейся точки на экране Э имеет вид светлого пятна. Для устранения сферической аберрации и создают систему из вогнутой и выпуклой линз.

Астигматизм¹

Это недостаток оптической системы, при которой сферическая световая волна, проходя оптическую систему, деформируется и перестает быть сферической. Различают два вида астигматизма. Один из них обусловлен падением на оптическую систему лучей, составляющих значительный угол с оптической осью (астигматизм косых пучков).

Пусть точка А предмета расположена вне главной оптической оси (рис. 26.2, а); из всех лучей, идущих от этой точки, выделим элементарный пучок таким образом, чтобы его центральный луч AS лежал в одной плоскости с главной оптической осью ОО'. Любую плоскость, проходящую через главную оптическую ось, называют меридиональной; в данном примере возьмем плоскость, в которой лежат центральный луч элементарного пучка и главная оптическая ось (на рис. 26.2, а - плоскость чертежа).

При наклонном падении элементарного пучка линза создаст два изображения точки А в виде отрезков прямой. Один из них лежит в меридиональной плоскости и отчетливо виден на экране II (рис. 26.2, а), другой - в перпендикулярной плоскости, которую называют сагиттальной, он отчетливо виден на экране I. В промежутке между плоскостями I и II наблюдается пятно рассеяния, имеющее форму эллипса или окружности (рис. 26.2, б). Если предметом является отрезок линии, то качество изображения зависит от ориентации отрезка. Отрезки, расположенные в меридиональных плоскостях², дают четкое изображение в плоскости II, а расположенные в сагиттальных плоскостях - в плоскости I.

¹ Астигматизм - не точечный. Точке предмета соответствует не одна точка изображения.

² Предполагается, что предмет лежит в плоскости, перпендикулярной главной оптической оси.

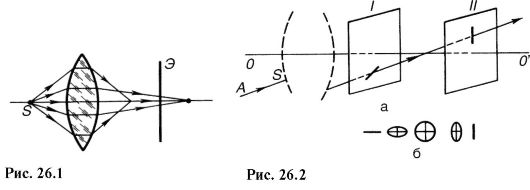
Для демонстрации астигматизма косых пучков удобна сетка, представленная на рис. 26.3, а. Помещая ее как предмет перпендикулярно оптической оси, зададим систему отрезков, лежащих в меридиональных плоскостях (радиусы) и сагиттальных (окружности). На рис. 26.3, б, в показаны изображения этих отрезков, полученные в соответствующих плоскостях.

Для исправления астигматизма создают сложные оптические системы, состоящие из нескольких линз, благодаря чему удается образовать хорошие изображения при углах падения лучей 50-70°.

Другой вид астигматизма обусловлен асимметрией оптической системы. Линзы с такой аберрацией называют астигматическими. Эти линзы, аналогично астигматизму косых пучков, создают изображение, в котором контуры и линии, ориентированные в разных направлениях, имеют разную резкость.

Наиболее наглядно астигматизм такого типа можно продемонстрировать на цилиндрической линзе (рис. 26.4). Пучок лучей, параллельных главной оптической оси, преломляется линзой l только в плоскостях, перпендикулярных образующей цилиндра, поэтому на экране Э, расположенном в фокальной плоскости линзы, наблюдается прямая линия, а не точка, как при сферических линзах. Если с помощью цилиндриче-

ской линзы отобразить на экране сетку из тонкой проволоки с квадратными ячейками (рис. 26.5, а), то наиболее четкое изображение получается в виде системы параллельных линий, направленных вдоль образующей цилиндра (рис. 26.5, б, в; изображения соответствуют двум взаимно перпендикулярным положениям цилиндрической линзы).

Дисторсия

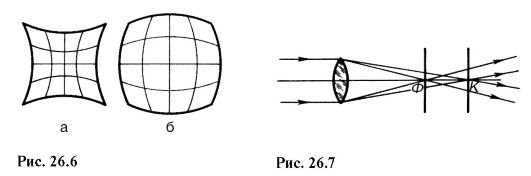
Этот вид аберрации возникает вследствие того, что лучи, посылаемые предметом в систему, составляют большие углы с оптической осью, при этом зависимость линейного увеличения от угла пучка приводит к нарушению подобия изображения и предмета. Типичные проявления дисторсии показаны на рис. 26.6: а - подушкообразная; б - бочкообразная; предметом является сетка с квадратными ячейками.

Подбирая систему из нескольких линз с противоположным характером дисторсии, можно исправить эту аберрацию.

Хроматическая аберрация

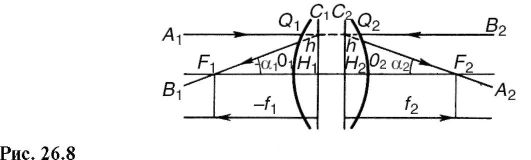
Как видно из (26.2), фокусное расстояние линзы определяется показателем преломления, который зависит от длины волны. Поэтому пучок белого света, идущий параллельно главной оптической оси, будет фокусироваться в разных ее точках, разлагаясь в спектр (рис. 26.7: Ф - фиолетовые лучи; К - красные), кружок на экране окажется окрашенным. В этом заключается хроматическая аберрация, которая очень часто сопутствует изображениям в линзах.

Для исправления этого вида аберрации создают ахроматические оптические системы из линз, которые изготовляют из стекол с разной дисперсией: ахроматы и апохроматы.

В оптических устройствах используют системы из линз, называемые анастигматами, в которых исправлены не только хроматическая аберрация, но и сферическая, и астигматизм.

Существуют и другие виды аберраций, которые здесь не рассматриваются.

Одновременное устранение всех аберраций может оказаться слишком сложной или даже неразрешимой задачей, поэтому обычно избавляются только от тех погрешностей, которые существенно мешают основному назначению оптической системы. Так, для объективов микроскопов важно устранение сферической аберрации, возникающей при рассматривании объектов, лежащих вблизи фокуса и отображаемых широкими пучками.

26.3. ПОНЯТИЕ ОБ ИДЕАЛЬНОЙ

ЦЕНТРИРОВАННОЙ ОПТИЧЕСКОЙ СИСТЕМЕ

Реальные оптические системы состоят из различных деталей и часто включают в себя несколько линз (см. 26.2). При произвольном расположении линз расчет и построение изображений могут быть достаточно сложными.

Практически часто используют системы сферических поверхностей (линз), центры которых лежат на одной прямой - главной оптической оси. Такие оптические системы называют центрированными.

Рассмотрим некоторые выводы теории идеальной центрированной оптической системы, предложенной Гауссом. В этой системе каждой точке или линии пространства предметов соответствует только одна точка или линия пространства изображений. Пары точек или линий обоих пространств называют сопряженными. К идеальной центрированной оптической системе приближаются такие, в которых использу-

ются параксиальные лучи. Эта система есть физическая абстракция, позволяющая рассчитывать реальные системы с учетом степени их отклонения от идеальной.

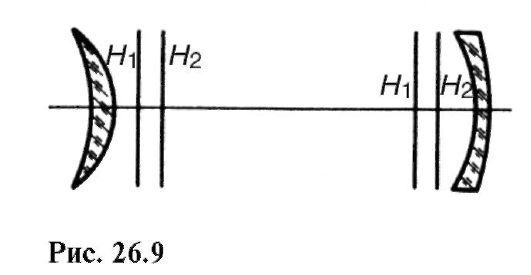
Укажем характерные точки и плоскости центрированной оптической системы (рис. 26.8; Q₁ и Q₂ - крайние сферические поверхности), принятые в теории Гаусса, с помощью которых можно определить изображения предметов.

Проведем в пространстве предметов луч А₁, параллельный главной оптической оси O₁O₂. В пространстве изображений ему сопряжен луч А₂, проходящий через точку F₂. Точка F₂ пространства изображений, сопряженная бесконечно удаленной точке пространства предметов, является вторым, или задним, фокусом системы.

Аналогично, лучу В₂ пространства изображений соответствует луч В₁ пространства предметов, проходящий через точку F₁. Точка F₁ пространства предметов, сопряженная бесконечно удаленной точке пространства изображений, является первым, или передним, фокусом¹.

Плоскости, проходящие через фокусы перпендикулярно главной оптической оси, называют фокальными.

Так как лучи А₁ и В₁ попарно сопряжены А₂ и В₂, то сопряжены и точки С₁ и С₂ пересечения этих лучей или их продолжений. Проведя через С₁ и С₂ плоскости, перпендикулярные O₁O₂, получим точки Н₁ и Н₂. Имеем попарное сопряжение этих плоскостей, точек Н₁ и Н₂ и отрезков С₁Н₁ и С₂Н₂. Отрезки С₁Н₁ и С₂Н₂ не только сопряжены, но и равны (\C₁ff₁\ = \C₂ff₂\ =h) и имеют одинаковое направление относительно оптической оси (одинаковые знаки); следовательно, для них линейное увеличение β = +1. Оптическая система имеет две сопряженные плоскости, перпендикулярные оптической оси, для которых линейное увеличение сопряженных отрезков β = +1; такие плоскости и соответствующие точки Н₁ и Н₂ главной оптической оси называют главньми.

¹ Так как пространства предметов и изображений взаимно сопряжены, то понятия «передний» и «задний», «первый» и «второй» условны.

Расстояния между фокусами и соответствующими главными точками называют фокусными:

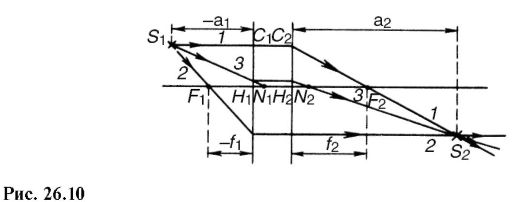
Главные плоскости и точки н₁ и Н₂ могут лежать не только внутри центрированной оптической системы (рис. 26.8), но и вне ее, совершенно не симметрично относительно граничных поверхностей (рис. 26.9).

Главные точки и фокусы называют кардинальными точками, а соответствующие плоскости - кардинальными плоскостями. Эти точки и плоскости используют для построения изображения безотносительно к истинному ходу лучей в системе. Общие принципы аналогичны правилам построения изображения в тонкой линзе.

На рис. 26.10 показан пример построения изображения в центрированной оптической системе. Луч 1, идущий от светящейся точки S₁ параллельно главной оптической оси, продолжают до пересечения с главной плоскостью пространства изображений, а затем проводят через фокус F₂. Луч 2 проходит через фокус F₁ до пересечения с главной плоскостью пространства предметов, а затем параллельно оптической оси. Пересечение двух лучей (точка s₂) и дает изображение точки s₁.

Точки n₁ и N₂ (рис. 26.10) называют узловыми. Их особенность заключается в том, что сопряженные лучи 3, проходящие через них, одинаково наклонены к оптической оси.

Если по обе стороны от оптической системы находятся среды с одинаковыми показателями преломления, то узловые точки совпадают с соответствующими главными точками.

Таким образом, оптическая система характеризуется шестью кардинальными точками и шестью кардинальными плоскостями.

Приведем без вывода наиболее важные формулы для центрированной оптической системы:

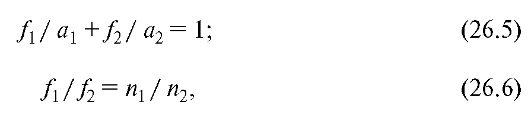
где n₁ и n₂- показатели преломления среды соответственно слева и справа от крайних сферических поверхностей оптической системы; обозначения а₁, a₂, f₁, f₂ разъяснены на рис. 26.10. Отрезки а₁ и f₁ отсчиты-ваются от главной точки Н₁, а отрезки a₂ и f₂ - от Н₂. Они считаются положительными, если их направление совпадает с направлением распространения света, и отрицательными, если противоположно. Обычно в геометрической оптике на рисунках принято распространение света слева направо.

Так как тонкая линза является частным случаем центрированной оптической системы, то естественно, что все сказанное выше справедливо и для нее. В этом случае четыре кардинальные точки - главные и узловые - совпадают с центром линзы, а формула (26.5) превращается в (26.3). Правила построения изображения в таких линзах, известные читателю из средней школы, также являются частным случаем более общего метода, описанного выше.

26.4. ОПТИЧЕСКАЯ СИСТЕМА ГЛАЗА И НЕКОТОРЫЕ ЕЕ ОСОБЕННОСТИ

Глаз человека является своеобразным оптическим прибором, занимающим в оптике особое место. Это объясняется, во-первых, тем, что многие оптические инструменты рассчитаны на зрительное восприятие, во-вторых, глаз человека (и животного), как усовершенствованная в процессе эволюции биологическая система, приносит в рамках бионики некоторые идеи по конструированию и улучшению оптических систем.

Для медиков глаз не только орган, способный к функциональным нарушениям и заболеваниям, но и источник информации о некоторых неглазных болезнях.

Остановимся кратко на строении глаза человека.

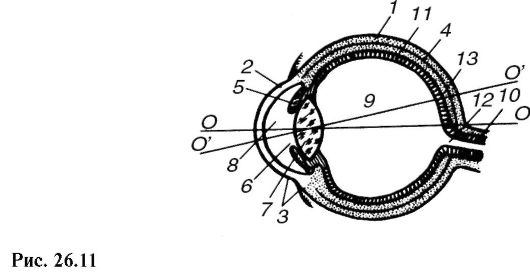
Собственно глазом (рис. 26.11) является глазное яблоко, имеющее не совсем правильную шаровидную форму: передне-задний размер у взрослого в среднем 24,3 мм, вертикальный - 23,4 мм и горизонтальный - 23,6 мм. Стенки глаза состоят из трех концентрически расположенных оболочек: наружной, средней и внутренней. Наружная белковая оболочка - склера 1 - в передней части глаза превращается в прозрачную выпуклую роговую оболочку 2 - роговицу. Толщина роговицы в центре около 0,6 мм, на периферии - до 1 мм. По оптическим свойствам роговица - наиболее сильно преломляющая часть глаза. Она является как бы окном, через которое в глаз проходят лучи света. Радиус кривизны роговицы примерно 7-8 мм, показатель преломления ее вещества - 1,38. Наружный покров роговицы переходит в конъюнктиву 3, прикрепленную к векам.

К склере прилегает сосудистая оболочка 4, внутренняя поверхность которой выстлана слоем темных пигментных клеток, препятствующих внутреннему диффузному рассеянию света в глазу. В передней части глаза сосудистая оболочка переходит в радужную 5, в которой имеется круглое отверстие - зрачок 6. Непосредственно к зрачку с внутренней стороны глаза примыкает хрусталик 7 - прозрачное и упругое тело, подобное двояковыпуклой линзе. Диаметр хрусталика 8-10 мм, радиус кривизны передней поверхности в среднем 10 мм, задней - 6 мм. Показатель преломления вещества хрусталика несколько больше - 1,4¹.

Между роговицей и хрусталиком расположена передняя камера 8 глаза, она заполнена водянистой влагой - жидкостью, близкой по опти-

¹ Строение хрусталика напоминает слоистую структуру лука, причем показатель преломления слоев неодинаков. Вследствие этой специфики хрусталик преломляет так, как однородное вещество с показателем преломления, большим показателя преломления любого слоя.

ческим свойствам к воде. Вся внутренняя часть глаза от хрусталика до задней стенки занята прозрачной студенистой массой, называемой стекловидным телом 9. Показатель преломления стекловидного тела такой же, как и у водянистой влаги.

Рассмотренные выше элементы глаза в основном относятся к его светопроводящему аппарату.

Зрительный нерв 10 входит в глазное яблоко через заднюю стенку; разветвляясь, он переходит в самый внутренний слой глаза - сетчатку, или ретину 11, являющуюся световоспринимающим (рецепторным) аппаратом глаза. Сетчатка состоит из нескольких слоев и неодинакова по своей толщине и чувствительности к свету, в ней находятся светочувствительные зрительные клетки, периферические концы которых имеют различную форму. Продолговатые окончания называют палочками, конусообразные - колбочками. Длина палочек 63-81 мкм, диаметр около 1,8 мкм, для колбочек соответственно 35 и 5-6 мкм. На сетчатке глаза человека расположено около 130 млн палочек и 7 млн колбочек.

В месте вхождения зрительного нерва находится не чувствительное к свету слепое пятно 12. В середине сетчатки, чуть ближе к височной области, лежит самое чувствительное к свету желтое пятно 13, центральная часть которого имеет диаметр около 0,4 мм.

Колбочки и палочки распределены по сетчатке неравномерно. Колбочки расположены главным образом в центральной части сетчатки, в желтом пятне, в центре желтого пятна находятся исключительно колбочки, на краях сетчатки - только палочки.

Рассмотрим сначала особенности светопроводящего аппарата глаза.

Глаз может быть представлен как центрированная оптическая система, образованная роговицей, жидкостью передней камеры и хрусталиком (четыре преломляющие поверхности) и ограниченная спереди воздушной средой, сзади - стекловидным телом. Главная оптическая ось OO (рис. 26.11) проходит через геометрические центры роговицы, зрачка и хрусталика. Кроме того, различают еще зрительную ось ОС глаза, которая определяет направление наибольшей светочувствительности и проходит через центры хрусталика и желтого пятна. Угол между главной оптической и зрительной осями составляет около 5°.

На рис. 26.12 показаны фокусы, главные точки и плоскости и узловые точки для некоторого усредненного нормального глаза (расстояния указаны в миллиметрах). Для упрощения часто заменяют эту систему приведенным редуцированным глазом, т.е. линзой, окруженной воздухом со стороны пространства предметов и жидкостью с « = 1,336 со стороны пространства изображений. В одной из моделей приведенного глаза

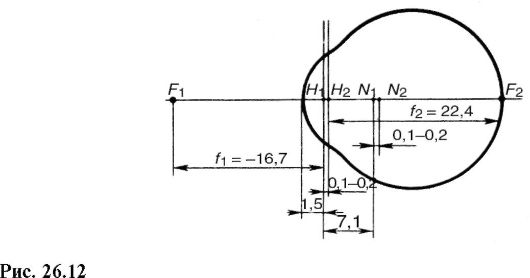
единая главная плоскость находится на расстоянии 1,6 мм от передней поверхности роговицы, узловые точки совпадают и расположены на расстоянии 7,2 мм от поверхности роговицы.

Основное преломление света происходит на внешней границе роговицы, оптическая сила всей роговицы равна приблизительно 40 дптр, хрусталика - около 20 дптр, а всего глаза - около 60 дптр.

Различно удаленные предметы должны давать на сетчатке одинаково резкие изображения. Из формулы (26.5) видно, что это можно осуществить либо изменяя расстояние a₂ между главной плоскостью и сетчаткой аналогично тому, как это делают в фотоаппаратах, либо изменяя кривизну хрусталика и, следовательно фокусные расстояния /₁ и /₂.В глазу человека реализуется второй случай.

Приспособление глаза к четкому видению различно удаленных предметов - «наводка на резкость» - называют аккомодацией¹.

Когда предмет расположен в бесконечности, то его изображение в нормальном глазу находится на сетчатке. Хрусталик при этом аккомодирован на бесконечность и его оптическая сила наименьшая. Если предмет приближается к глазу, то у хрусталика увеличивается кривизна; чем ближе предмет, тем больше оптическая сила глаза, ее изменения происходят приблизительно в пределах 60-70 дптр.

У взрослого здорового человека при приближении предмета к глазу до расстояния 25 см аккомодация совершается без напряжения и благодаря привычке рассматривать предметы, находящиеся в руках, глаз чаще всего аккомодирует именно на это расстояние, называемое расстоянием наилучшего зрения.

¹ У некоторых рыб аккомодация происходит за счет перемещения хрусталика в целом относительно оптической оси, т.е. реализуется первый случай.

Для рассматривания еще более близких предметов приходится уже напрягать аккомодационный аппарат. Наиболее близкое расположение предмета от глаза, при котором еще возможно четкое изображение на сетчатке, называют ближней точкой глаза (ближная точка ясного видения). Расстояние до ближней точки глаза с возрастом увеличивается; следовательно, аккомодация уменьшается.

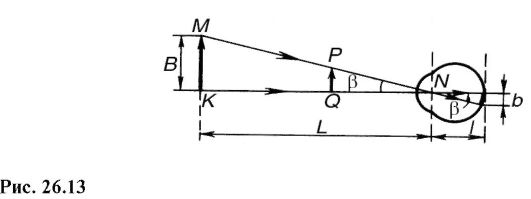
Размер изображения на сетчатке зависит не только от размера предмета, но и от его удаления от глаза, т.е. от угла, под которым виден предмет. В связи с этим вводят понятие угла зрения. Это угол между лучами, идущими от крайних точек предмета через совпадающие узловые точки (рис. 26.13). Из рисунка видно, что, во-первых, один и тот же угол зрения β может соответствовать разным предметам КМ и QP, и, во-вторых, что угол зрения вполне определяет размер изображения на сетчатке:

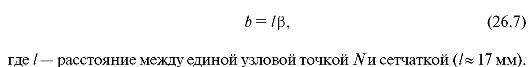
Формула (26.7) получена в предположении, что угол зрения мал.

Из рис. 26.13 легко установить связь между размером B предмет; расстоянием L его от глаза, точнее от узловых точек, и углом зрения β:

Для характеристики разрешающей способности глаза используют наименьший угол зрения, при котором человеческий глаз еще различает две точки предмета. Этот угол приблизительно равен 1', что соответствует [см. (26.8)] расстоянию между точками, равному 70 мкм, если они на-

ходятся на расстоянии наилучшего зрения. Размер изображения на сетчатке в этом случае [см. (26.7)] равен 5 мкм, что соответствует среднему расстоянию между двумя колбочками на сетчатке. Поэтому если изображение двух точек на сетчатке займет линию короче 5 мкм, то эти точки не разрешатся, т.е. глаз их не различает.

Такое же значение наименьшего угла зрения будет получено, если учесть ограничения, которые накладывает дифракция света (см. 26.8). Поражает целесообразность природы - ничего лишнего: число колбочек, приходящихся на единицу площади сетчатки, отвечает предельным возможностям геометрической оптики.

В медицине разрешающую способность глаза оценивают остротой зрения. За норму остроты зрения принимается единица, в этом случае наименьший угол зрения равен 1 .

При отклонениях острота зрения во столько раз меньше нормы, во сколько раз наименьший угол зрения больше минуты. Если наименьший угол зрения равен 4 , то острота зрения равна 1:4 = 0,25.

В отдельных случаях глаз человека различает и более мелкие величины, чем те, которые соответствуют углу 1 . Так, например, смещение движущихся предметов заметно, когда оно достигает 20 по дуге, несовпадение двух тонких линий обнаруживается уже при угле 12 между ними и т.д. В физических измерениях часто применяют приборы, в которых стрелка не должна смещаться с нулевого деления (штриха) шкалы (потенциометры, мосты). Благодаря способности глаза обнаруживать малые смещения линий такие приборы могут давать более точные показания, чем те, в которых определяется расстояние между штрихом и стрелкой¹.

Чувствительность глаза к свету и цвету, а также биофизические вопросы зрения рассматриваются в седьмом разделе.

26.5. НЕДОСТАТКИ ОПТИЧЕСКОЙ СИСТЕМЫ ГЛАЗА И ИХ УСТРАНЕНИЕ

Аберрации, свойственные линзам, у глаз почти не ощущаются.

Сферическая аберрация незаметна ввиду малости зрачка и проявляется лишь в сумерках, когда зрачок расширен: изображения нерезки. Хотя глаз и не является ахроматической системой, однако хроматическая аберрация не ощущается из-за избирательности видности излуче-

¹ Это вопрос не только физический, но и физиологический.

ния и малого размера зрачка. Астигматизм косых пучков не имеет места, так как глаз всегда устанавливается в направлении наблюдаемого предмета. Исключение составляет лишь астигматизм, обусловленный асимметрией оптической системы (несферическая форма роговицы или хрусталика). Это проявляется, в частности, в неспособности глаза одинаково резко видеть взаимно перпендикулярные линии на испытательной таблице. Такой недостаток глаза компенсируют специальными очками с цилиндрическими линзами.

Оптической системе глаза свойственны некоторые специфические недостатки.

В нормальном глазу при отсутствии аккомодации задний фокус совпадает с сетчаткой - такой глаз называют эмметропическим, и аме-тропическим, если это условие не выполняется.

Наиболее распространенными видами аметропии являются близорукость (миопия) и дальнозоркость (гиперметропия). Близорукость - недостаток глаза, состоящий в том, что задний фокус при отсутствии аккомодации лежит впереди сетчатки; в случае дальнозоркости задний фокус при отсутствии аккомодации лежит за сетчаткой. Для коррекции близорукого глаза применяют рассеивающую линзу, дальнозоркого - собирающую.

26.6. ЛУПА

Возможность разрешения деталей предмета зависит от размеров его изображения на сетчатке глаза или от угла зрения. Угол зрения можно увеличить, приблизив предмет к глазу, однако это связано с некоторыми ограничениями:

1) в ряде случаев технически невозможно существенно изменить расстояние между предметом и глазом (например, при рассмотрении звезд или Солнца);

2) невозможно приблизить предмет на расстояние меньшее предельных возможностей точки глаза, до ближней аккомодации.

В связи с этим для увеличения угла зрения используют оптические приборы: телескопы, лупы, микроскопы и т.п.

Рассмотрим устройство одного из наиболее простых оптических приборов - лупы.

Лупой называют оптическую систему, в передней фокальной плоскости которой или в непосредственной близости от нее расположен наблюдаемый предмет.

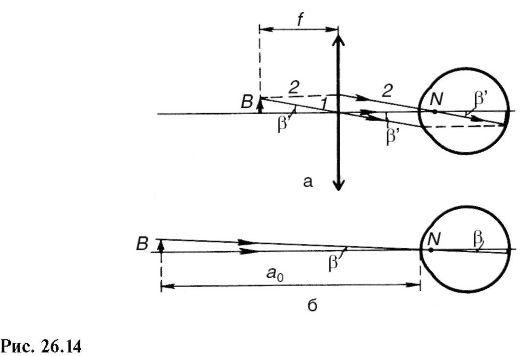
Изображение, создаваемое лупой, находится в бесконечности или на удобном для глаза расстоянии. Если изображение в бесконечности, то оно наблюдается глазом без аккомодации.

На рис. 26.14, а показано двумя лучами, как с помощью лупы формируется изображение на сетчатке; N - объединенная узловая точка оптической системы глаза, предмет помещен в передней фокальной плоскости. Луч 1 проходит через центр лупы без преломления, а затем преломляется глазом. Другие лучи, идущие от этой же точки предмета, после преломления в лупе будут параллельны лучу 1. Чтобы определить положение изображения на сетчатке, выберем из этих лучей тот, который проходит через объединенную узловую точку (луч 2). Он не преломляется глазом. Его пересечение с сетчаткой и укажет положение изображения предмета. Остается лишь для полноты картины достроить начальную часть луча 2 и конечную часть луча 1 (показаны пунктиром).

Увеличением лупы называют отношение угла зрения β', под которым видно изображение предмета (рис. 26.14, а), к углу зрения β, под которым виден предмет, находящийся на расстоянии наилучшего зрения а₀ = 25 см (рис. 26.14, б). Из рисунков видно:

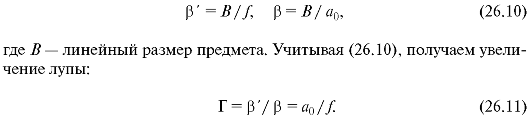
Отсюда видно, что формула для увеличения связывает постоянную величину f лупы с расстоянием наилучшего зрения - довольно условной величиной. У близорукого глаза расстояние наилучшего зрения а_б < 25 см, у дальнозоркого а_д > 25 см, поэтому для близорукого глаза увеличение от одной и той же лупы будет меньше, чем для дальнозоркого.

Учитывая, что напряжение аккомодации сильно утомляет глаз и допустимо лишь как кратковременное явление, следует при пользовании лупой помещать предмет в фокальную плоскость, а глаз - у самой лупы.

Лупы изготовляют из одной или нескольких линз. Увеличение лупы зависит от ее конструкции и изменяется в пределах от 2 до 40-50. Наиболее распространены лупы с 10-кратным увеличением.

Разрешаемое с помощью лупы расстояние между двумя точками можно вычислить по формуле (26.8). Например, если для 10-кратного увеличения взять β = 0,1' и 3 ?10^-5 рад; L = а₀ = 0,25 м, то получим В = 0,25 ?3 ? 10^-5 = 7,5 мкм.

26.7. ОПТИЧЕСКАЯ СИСТЕМА И УСТРОЙСТВО БИОЛОГИЧЕСКОГО МИКРОСКОПА

Для получения больших увеличений в качестве лупы следует использовать [см. (26.11)] короткофокусные линзы. Однако такие линзы имеют небольшие размеры, им свойственны значительные аберрации, что накладывает ограничения на увеличение лупы. Большее увеличение можно получить, рассматривая через лупу действительное изображение предмета, созданное дополнительной линзой или системой линз. Таким оптическим устройством является микроскоп. Лупу в этом случае называют окуляром, а дополнительную линзу или систему линз - объективом.

Для того чтобы глаз не был напряжен, стремятся совместить изображение, созданное объективом, с фокальной плоскостью окуляра. На рис. 26.15 показан ход лучей в микроскопе, объективом и окуляром которого являются собирающие линзы, и в глазу.

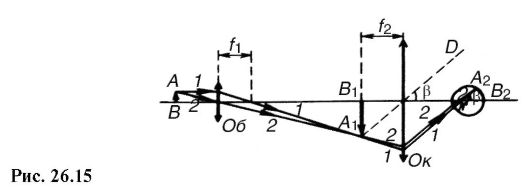
Изображение А₁В₁ предмета АВ, созданное линзой объектива Об, находим согласно правилу построения изображения в тонкой линзе; луч 1, параллельный главной оптической оси, проходит после преломления в линзе через фокус, луч 2 через центр линзы идет без преломления; А₁В₁ расположено в передней фокальной плоскости окуляра.

Лучи 1 и 2 доходят до линзы окуляра Ок и в ней преломляются. Чтобы показать ход этих лучей после преломления в окуляре, проведем следующее рассуждение.

Все лучи, идущие из некоторой точки фокальной плоскости (например, А₁), после преломления в линзе должны распространяться параллельно друг другу. Проведем из А₁ луч А₁D через центр линзы; лучи 1 и 2 после преломления в окуляре пройдут параллельно A₁D до встречи с глазом. Пусть луч 1 проходит через объединенную узловую точку N глаза и потому без преломления дойдет до точки А₂ сетчатки. В эту же точку сфокусируется луч 2. На сетчатке глаза получаем изображение А₂В₂ предмета АВ.

В современных оптических микроскопах объектив и окуляр состоят из системы линз, представляющей собой оптическую систему (рис. 26.16). Главные плоскости объектива и окуляра такой системы показаны на рисунке раздельно, окружающая среда имеет одинаковый показатель преломления. Лучи 1 и 2, идущие от точки В предмета АВ, пересекаются в точке В , где формируется изображение, создаваемое объективом. Луч 2 попадает на окуляр параллельно главной оптической оси, поэтому он проходит через фокус F₂ .Так как лучи 1 и 2 выходят из одной точки В фокальной плоскости, после преломления в окуляре они будут параллельны друг другу.

Можно указать главные точки и фокусы микроскопа как единой центрированной оптической системы. Так как луч 1 в пространстве

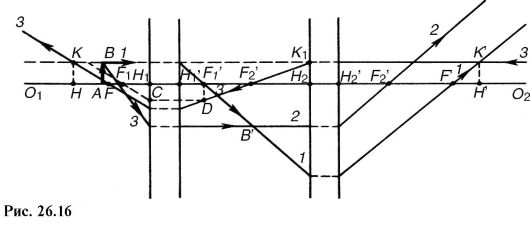
предметов параллелен главной оптической оси, то он в пространстве изображений пересечет оптическую ось в заднем фокусе F₁'.

Главные точки и плоскости найдем из условия, что точка и ее изображение, расположенные в соответствующих главных плоскостях, равноудалены от главной оптической оси.

Чтобы не загромождать чертеж, выберем точку К передней главной плоскости так, чтобы луч, распространяющийся от этой точки параллельно оптической оси, в пространстве предметов совпадал с лучом 1. Сопряженную ей точку К' , расположенную в задней фокальной плоскости, найдем из условия, что она лежит на луче 1 и удалена на такое же расстояние от главной оптической оси, как и точка К. Проецируя К' на главную оптическую ось, получаем заднюю главную точку И'.

Для нахождения передней главной точки из К' направим луч 3 параллельно главной оптической оси. Он пройдет через F₂ до пересечения с задней главной плоскостью объектива. Чтобы определить направление этого луча после выхода из передней главной плоскости объектива, сделаем дополнительное построение: из точки D, лежащей в фокальной плоскости, проводим луч DC параллельно главной оптической оси, он должен пройти через фокус F₁, а луч 3 пройдет параллельно CF₁. Пересечение луча 3 с главной оптической осью дает передний фокус F микроскопа, а с лучом 1 - положение точки К, которая лежит в передней главной плоскости; И - передняя главная точка микроскопа. Отметим, что в этом случае фокусы расположены между главными точками.

Так как показатели преломления среды пространств предмета и изображения одинаковы, то на основании (26.6) фокусные расстояния отличаются только знаком: f = - f'.

где Г_ок - увеличение окуляра; Г_об - увеличение объектива¹.

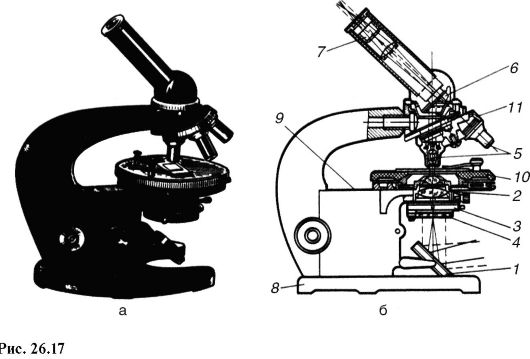
На рис. 26.17 изображены общий вид (а) и схема (б) биологического микроскопа МВР-1. Его главные части: основание 8, коробка с микро-

¹ Читателю из курса физики средней школы известна формула для увеличения линзы. Следует учесть, что предмет располагается вблизи фокуса объектива, поэтому расстояние предмета от линзы объектива приблизительно равно ее фокусному расстоянию. Так как оно невелико, то оптическую длину тубуса можно считать расстоянием от объектива до изображения.

метрическим механизмом 9, предметный столик 10, револьвер 11 с объективами 5, конденсор 2 и окуляр 7. Оптическая система состоит из двух частей: осветительной и наблюдательной. В осветительную часть входит зеркало 1, конденсор с ирисовой апертурной диафрагмой 3 и съемный светофильтр 4, а в наблюдательную - объектив, призма 6 и окуляр, соединенные в тубусе микроскопа.

Пучок лучей от источника света падает на зеркало, которое отражает его к диафрагме, проходит через конденсор и исследуемый препарат и затем попадает в объектив.

26.8. РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ И ПОЛЕЗНОЕ УВЕЛИЧЕНИЕ МИКРОСКОПА.

ПОНЯТИЕ О ТЕОРИИ АББЕ

Из формулы (26.15) можно сделать вывод, что при надлежащем выборе f₁ и f₂ увеличение микроскопа будет сколь угодно большим. Однако на практике биологи, врачи и другие специалисты, работающие с микроскопами, редко используют увеличения, превышающие 1500-2000. Чтобы уяснить причины такого положения, ознакомимся с понятиями «предел разрешения», «разрешающая способность» и «полезное увеличение микроскопа».

Предел разрешения - это такое наименьшее расстояние между двумя точками предмета, когда эти точки различимы, т.е. воспринимаются в микроскопе как две точки.

Разрешающей способностью обычно называют способность микроскопа давать раздельные изображения мелких деталей рассматриваемого предмета. Это величина обратна пределу разрешения. Разрешающая способность микроскопа обусловлена волновыми свойствами света, поэтому выражение для предела разрешения можно получить, учитывая дифракционные явления.

Рассмотрим дифракционную теорию разрешающей способности микроскопа, предложенную Э. Аббе.

При освещении прозрачного предмета в микроскоп попадает свет, рассеянный (дифрагированный) объектом. В качестве наиболее простого предмета была взята дифракционная решетка - объект с достаточно определенной структурой.

Пусть решетка Д (рис. 26.18) состоит из четырех щелей 1-4. От каждой щели распространяются вторичные волны, на рисунке показан ход пяти лучей от каждой такой волны. Вторичные волны, падающие под

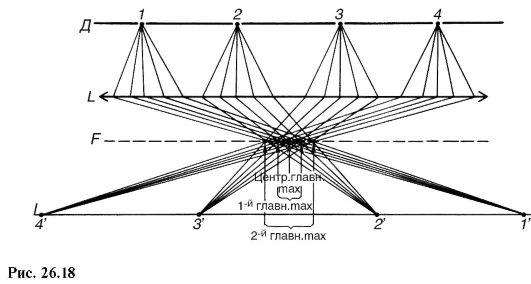
одинаковым углом к оптической оси линзы l, соберутся в фокальной плоскости f. Если разность хода вторичных волн, идущих от соседних щелей и отклоненных на одинаковый угол, равна целому числу длин волн, то в местах, обозначенных точками на плоскости f, появятся главные максимумы (центральный, 1-й, 2-й).

Картину, образуемую в фокальной плоскости линзы, называют первичным изображением. Оно содержит определенную информацию о предмете, однако не является изображением в общепринятом понимании.

Собственно изображение, или вторичное изображение (1-4), образуется в плоскости i при пересечении вторичных волн, идущих от каждой из щелей. Вторичное изображение создается после первичного, поэтому оно не может содержать большей информации о предмете, чем первичное.

В оптических устройствах, в том числе и в микроскопе, пучки света всегда ограничены, поэтому важно знать, как это повлияет на искажение изображения предмета, какое минимальное количество лучей способно передавать правильную информацию о предмете.

Главные максимумы попарно симметрично располагаются относительно центрального и в некоторой степени дублируют друг друга. Совокупность максимумов, расположенных с одной стороны от центра, вместе с центральным достаточна, чтобы передать информацию о предмете. Следовательно, экранирование лучей, идущих от максимумов, расположенных по другую сторону от центра, лишь уменьшит яркость изображения предмета.

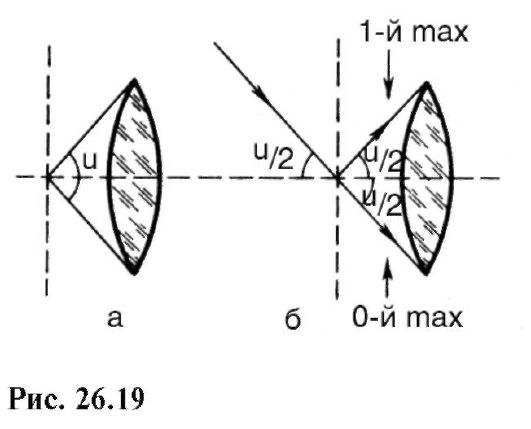
При экранировании в плоскости F лучей от нечетных главных максимумов объективно создаются условия, при которых второй главный максимум играет роль первого, четвертый - второго и т.д., т.е. [см. (24.29)] изображение будет такое же, как и у дифракционной решетки с вдвое меньшим периодом.

Центральный максимум имеет общую структуру для решеток с раз-

ным периодом и, следовательно, не содержит информации об особенностях предмета. Поэтому если пропустить лучи только центрального максимума, экранировав все остальные, то вторичное изображение предмета (решетки) не сформируется.

Такого рода опыты с различным ограничением пучков света в плоскости F проделал Аббе. Он установил, что для соответствия вторичного изображения предмету необходимо по крайней мере, чтобы из первичного изображения проходили дальше лучи центрального и одного из первых главных максимумов.

Реально свет от предмета распространяется к объективу микроскопа в некотором конусе (рис. 26.19, а), который характеризуется угловой апертурой - углом u между крайними лучами конического светового пучка, входящего в оптическую систему¹. В предельном случае, согласно Аббе, крайними лучами конического светового пучка будут лучи, соответствующие центральному (нулевому) и 1-му главному максимумам (рис. 26.19, б). При этом луч падает на предмет (решетку) под углом u/2, такой же угол и для первого дифракционного максимума. Из формулы (24.39) при β = u/2 и α = -u/2 получаем:

В рассмотренной модели предмета (решетка) за предел разрешения z следует принять элемент структуры - постоянную дифракционной решетки с, т.е. z = с при указанных α и β. Из (26.17) находим:

1 Предполагается, что объектив микроскопа наиболее сильно ограничивает световой поток, т.е. является апертурной диафрагмой.

или, учитывая, что λ = λ ₀/n, и вводя А = п sin(u/2),

z = 0,5λ ₀/А. (26.19)

где А - числовая апертура; п - показатель преломления среды, находящейся между предметом и линзой объектива.

Как видно из формулы (26.19), один из способов уменьшения предела разрешения микроскопа - использование света с меньшей длиной волны. В связи с этим применяют ультрафиолетовый микроскоп, в котором микрообъекты исследуются в ультрафиолетовых лучах. Принципиальная оптическая схема такого микроскопа аналогична схемам обычного микроскопа. Основное отличие заключается, во-первых, в использовании оптических устройств, прозрачных для ультрафиолетового света, и, во-вторых, в особенности регистрирования изображения. Так как глаз непосредственно не воспринимает этого излучения, то употребляются фотопластинки, люминесцентные экраны или электронно-оптические преобразователи (см. раздел седьмой).

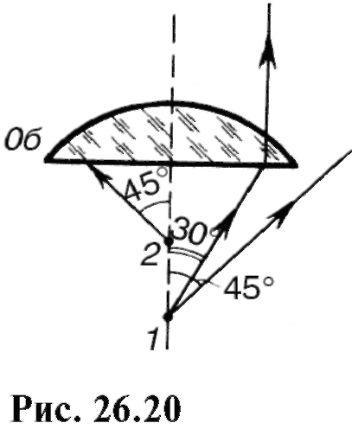
Другой способ уменьшения предела разрешения микроскопа - увеличение числовой апертуры, что достигается увеличением как показателя преломления среды между предметом и объективом, так и апер-турного угла. В обычных условиях (воздух) показатель преломления равен единице. Угол же и/2 может иметь большие значения - теоретически до 90°. Если этот угол очень велик, то лучи первого максимума могут не попасть в объектив. Так, например, на рис. 26.20 показано, что объектив Об не захватывает лучей, отходящих от точки 1 под углом 45°. Чтобы эти лучи попали, надо предмет приблизить к объективу, например в точку 2. Однако расстояние предмета от линзы не может изменяться произвольно, оно постоянно для каждого объектива и приближать предмет нельзя.

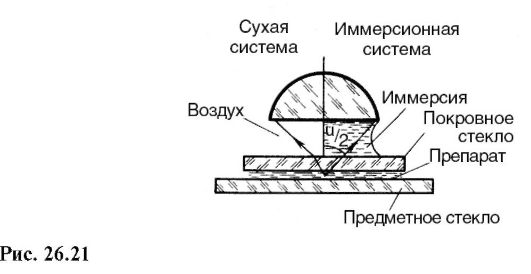
Числовая апертура может быть увеличена с помощью специальной жидкой среды - иммерсии - в пространстве между объективом и покровным стеклом микроскопа. В иммерсионных системах по сравнению с тождественными сухими системами получают больший апертур-ный угол (рис. 26.21). В качестве иммерсии используют воду (n = 1,33), кедровое масло (п = 1,515), монобромнафталин (n = 1,66) и др. Для каждой иммерсии специально рассчитывают объектив, и его можно применять только с данной иммерсией.

В современных микроскопах угол u/2 достигает наибольшего значения, равного 70°. С этим углом получают максимальные числовые апертуры и минимальные пределы разрешения (табл. 26.1).

Таблица 26.1

Данные приведены для наклонного падения света на объект и наиболее чувствительной глазу длины волны 0,555 мкм.

Условия освещения объекта влияют на разрешающую способность микроскопа, что важно учитывать в биологических исследованиях.

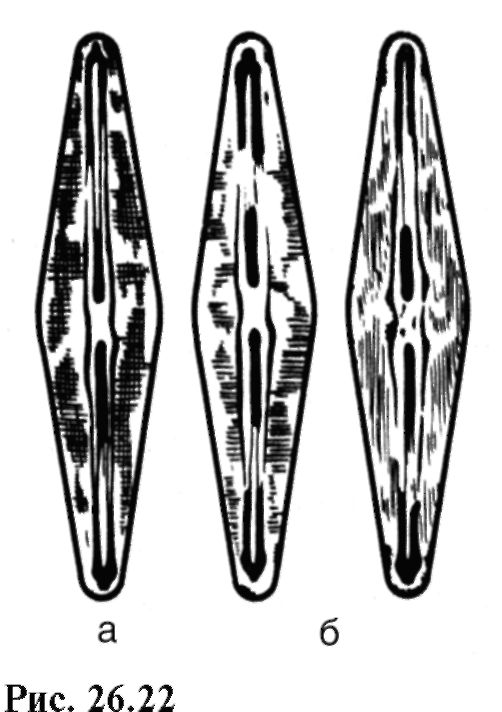
Известен курьез, когда исследователи-биологи отнесли к разным видам диатомею, так как разные условия освещения выявляли иначе структуру ее панциря. На рис. 26.22 показан вид объекта при полном (а) и частичном (б) разрешении из-за разного освещения.

Заметим, что окуляр совершенно не влияет на разрешающую способность микроскопа, он только создает увеличенное изображение объектива.

Оценим полезное увеличение микроскопа, используя формулу (26.19).

Если предмет имеет размер, равный пределу разрешения z, a размер его изображения z и если это изображение расположено на расстоянии наилучшего зрения от глаза, то увеличение микроскопа:

Нормальный глаз в предельном случае различает две точки предмета, угловое расстояние между которыми равно 1 (см. 26.4). Считают, что удобная различимость должна соответствовать углу зрения в интервале от 2 до 4' или значениям z (на расстоянии наилучшего зрения) от 140 до 280 мкм. Подставляя их, а также λ₀ = 0,555 мкм в формулу (26.20), находим интервал значений увеличения микроскопа:

Эти увеличения называют полезными, так как при них глаз различает все элементы структуры объекта, которые разрешимы микроскопом.

Подставляя числовую апертуру иммерсионной системы с маслом (А = 1,43) в (26.21), получаем следующее неравенство для полезных увеличений такого микроскопа: 700 < Г < 1400.

26.9. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ПРИЕМЫ ОПТИЧЕСКОЙ МИКРОСКОПИИ

Измерение размеров микроскопических объектов с помощью микроскопа

Применяют окулярный микрометр - круглую стеклянную пластинку, на которой нанесена шкала с делениями. Микрометр устанавливают в плоскости изображения, получаемого от объектива.

При рассматривании в окуляр изображения объекта и шкалы сливаются и можно отсчитать, какое расстояние по шкале соответствует измеряемой величине. Отсчет по шкале еще не дает размера объекта, так как совмещаемое со шкалой изображение не равно размеру предмета. Надо найти цену одного деления окулярного микрометра, для этого

применяют объектный микрометр - шкалу с делениями по 0,01 мм. Рассматривая объектный микрометр как предмет, совмещают в одном поле зрения две шкалы - объектную и окулярную - и определяют цену деления окулярного микрометра.

Вместо объектного микрометра можно применить любой препарат, размер которого известен, или использовать счетную камеру Горяева, употребляемую в медицинских измерениях.

В настоящее время широко применяют окулярно-винтовой микрометр, внешний вид которого изображен на рис. 26.23. Этот прибор устанавливают вместо окуляра. При вращении винта перемещается перекрестие, что позволяет отсчитывать доли делений микрометра.

Окулярно-винтовой микрометр нуждается в предварительной градуировке.

Микропроекция и микрофотография

Формирование микроскопического изображения происходит с участием человека и завершается образованием действительного изображения в глазу.

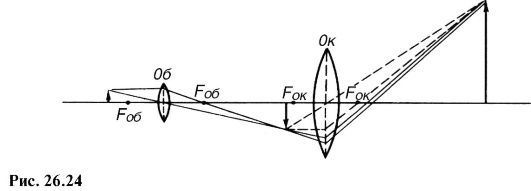
Обычный микроскоп сам по себе не создает действительного изображения, однако для фотографирования (микрофотография) или проекции микроскопического изображения на экран (микропроекция) должно быть получено действительное изображение. Для этого изображение, даваемое объективом Об, надо расположить дальше фокусного расстояния окуляра Ок (рис. 26.24).

Метод фазового контраста

Интенсивность световой волны, проходящей через прозрачный объект, почти не изменяется, но фазы претерпевают изменения, зависящие от толщины объекта и его показателя преломления. В этом смысле прозрачные объекты называют дефазирующими. Увидеть детали таких объектов обычным образом невозможно. В биологических исследованиях такие объекты иногда окрашивают, однако при этом могут изменяться их свойства и жизнеспособность.

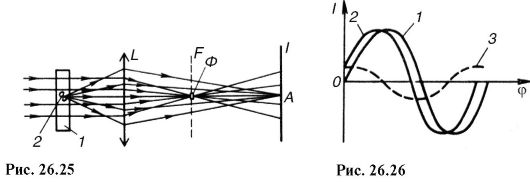
Для рассмотрения деталей дефазирующих объектов Ф. Цернике предложил метод фазового контраста. Пусть объект состоит из однородной прозрачной среды 1 с показателем преломления n, в которой имеется прозрачное включение 2, например бактерия с показателем преломления n₁ (рис. 26.25). При попадании плоскопараллельного пучка света часть его будет проходить через прозрачный объект и линзой L фокусироваться в небольшом участке Ф фокальной плоскости F, а другая часть будет дифрагировать на неоднородности и соберется линзой в точке А плоскости I.

Фазовый состав световых колебаний в плоскости I графически в координатах интенсивность-фаза изображен на рис. 26.26. Кривая 1 соответствует прямому свету, прошедшему через объект без дифракции, кривая 2 - свету, дифрагированному объектом. Если n₁ > n₂, то эта кривая будет отставать по фазе, что и показано на рисунке. Кривую 2 можно представить как сумму двух волн. Одна из них (1) проходит объект без дифракции, другая (3) является результатом дифракции на бактерии с показателем преломления n₁. Кривую 3 можно найти графически, вычитая из ординат кривой 2 ординаты кривой 1 .

Глаз в плоскости I (см. рис. 26.25) не различает волны 1 и 2, так как их интенсивности одинаковые, а на различие фаз глаз не реагирует. Необходимо фазовый рельеф преобразовать в амплитудный.

Как видно из рис. 26.26, волна 3 сдвинута по фазе относительно волны 1 приблизительно на π/2, что соответствует оптической разности хо-

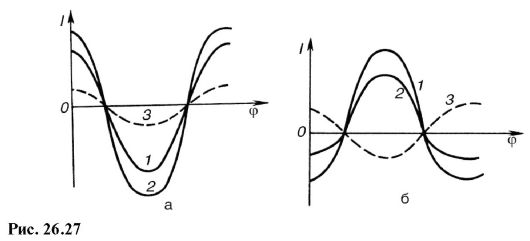
да λ/4. Если изменить фазу волны 1 на π/2, то волны 1 и 3 окажутся либо в фазе (рис. 26.27, а), либо в противофазе (рис. 26.27, б). Кривую 2 найдем графически как сумму ординат кривых 1 и 3. Из рисунка видно, что в этом случае волны 1 и 2 уже различаются по интенсивности (амплитуде), поэтому глаз заметит бактерию на однородном световом поле.

Так как волна 1 проходит в плоскости F (см. рис. 26.25) через небольшой участок, то можно, поставив в этом месте небольшую круглую пластинку (фазовую пластинку) Ф, изменить фазу волны. Иногда фазовую пластинку изготавливают из материала, который частично поглощает волну 1, в этом случае контраст бактерии будет еще более усилен, так как будет увеличена разница амплитуд волн 1 и 2.

Фазово-контрастные устройства (пластинки, конденсоры) обычно комплектуют как дополнительные приспособления к микроскопам.

Ультрамикроскопия

Это метод обнаружения частиц, размеры которых лежат за пределами разрешения микроскопа. Микроскопы, работающие по этому методу, называют ультрамикроскопами. В них осуществляют боковое (косое) освещение, благодаря чему субмикроскопические частицы видны как светлые точки на темном фоне; строение частиц увидеть нельзя.

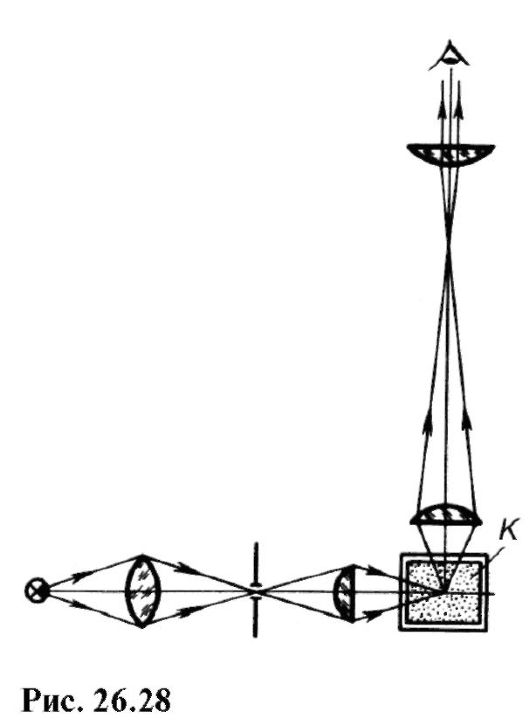
Принципиальная оптическая схема ультрамикроскопа изображена на рис. 26.28. Свет от источника попадает с левой стороны в кювету К с мелкими частицами аэрозолей, гидрозолей и т.п.; наблюдение проводят сверху. Этот метод позволяет регистрировать частицы размером до 2 мкм; его используют, в частности, с санитарно-гигиеническими целями для определения чистоты воздуха.

26.10. ВОЛОКОННАЯ ОПТИКА И ЕЕ ИСПОЛЬЗОВАНИЕ В МЕДИЦИНСКИХ ПРИБОРАХ

Традиционными элементами оптических систем, формирующих световой пучок, являются линзы, зеркала, призмы, плоскопараллельные пластинки и т.п. Начиная с 50-х годов нашего столетия к этим элементам прибавились волоконно-оптические детали, которые способны передавать свет по каналам, называемым светопроводами.

Волоконной оптикой называют раздел оптики, в котором рассматривают передачу света и изображения по светопроводам.

Этим же термином иногда называют и сами волоконно-оптические детали и приборы.

Волоконная оптика основана на явлении полного внутреннего отражения. Свет, попадая внутрь прозрачного волокна, окруженного веществом с меньшим показателем преломления, многократно отражается и распространяется вдоль этого волокна (рис. 26.29). Так как при полном отражении коэффициент отражения сравнительно высок (порядка 0,9999), то потери энергии в основном обусловлены поглощением света веществом внутри волокна. Так, например, в видимой области спектра в волокне длиной 1 м теряется 30-70% энергии.

Для передачи больших световых потоков и сохранения гибкости све-топроводящей системы отдельные волокна собираются в пучки (жгуты) - световоды. На рис. 26.30 схематически показан световод; из-за хаотического расположения волокон изображение цифры 1 искажено.

В медицине световоды используют для решения двух задач: передачи световой энергии, главным образом для освещения холодным светом внутренних полостей, и передачи изображения. Для первого случая не имеет значения положение отдельных волокон в световоде, для второго существенно, чтобы расположение волокон на входе и выходе световода было одинаковым.

Примером влияния волоконной

оптики на модернизацию существующих медицинских аппаратов является эндоскоп - специальный прибор для осмотра внутренних полостей (желудок, прямая кишка и др.). Он состоит из двух основных частей: источника света и смотровой части. Используя волоконную оптику, удалось, во-первых, свет от лампочки передавать внутрь органа по световоду, тем самым избегая нежелательного нагревания этого органа, которое неизбежно возникало при помещении источника света внутри полости в эндоскопах прежней конструкции; во-вторых, что самое главное, гибкость волоконно-оптических систем допускает осмотр большей части полостей, чем жесткие эндоскопы.

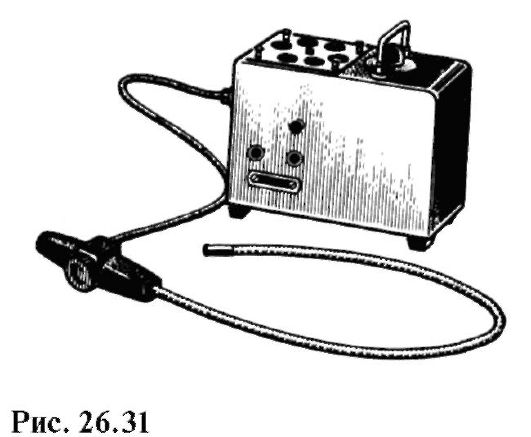
На рис. 26.31 показан волоконный гастроскоп. С его помощью можно не только визуально осмотреть желудок, но и произвести необходимые снимки с целью диагностики. Именно эти потребности медицины стимулировали развитие волоконной оптики вообще.

С помощью световодов осуществляется передача лазерного излучения во внутренние органы с целью лечебного воздействия на опухоли.

В заключение заметим, что сетчатка глаза человека является высокоорганизованной волоконно-оптической системой, состоящей примерно из 130 ? 10⁶ волокон. Это, вероятно, наиболее сложная волоконно-оптическая система, существующая в настоящее время.