Глава 18. Электромагнитные колебания и волны

Электромагнитными колебаниями называют периодические (или почти периодические) взаимосвязанные изменения зарядов, токов, напряженностей электрического и магнитного полей. Распространение электромагнитных колебаний в пространстве происходит в виде электромагнитных волн. Среди различных физических явлений электромагнитные колебания и волны занимают особое место. Почти вся электротехника, радиотехника и оптика базируется на этих понятиях.

18.1. СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ

Свободными (собственными) электромагнитными колебаниями называют такие, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.

Рассмотрим закрытый колебательный контур, состоящий из катушки индуктивности L и конденсатора С (рис. 18.1), который ключом К заряжается от источника ε, а затем разряжается на катушку индуктивности. При этом в контуре возникает э.д.с. самоиндукции, которая будет равна напряжению на обкладках конденсатора. Используя формулу (17.14), запишем:

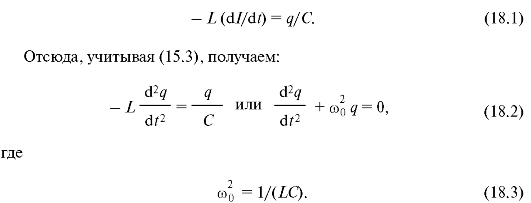
Известно, что (18.2) является дифференциальным уравнением гармонического колебания, его решение [см. (7.6)] имеет вид:

18.2. ПЕРЕМЕННЫЙ ТОК

В широком смысле слова переменный ток - любой ток, изменяющийся со временем. Однако чаще термин «переменный ток» применяют к токам, изменяющимся со временем по гармоническому закону. Переменный ток можно рассматривать как вынужденные электромагнитные колебания.

Представим три разных цепи (рис. 18.4, а-18.6, а), к каждой из которых приложено переменное напряжение:

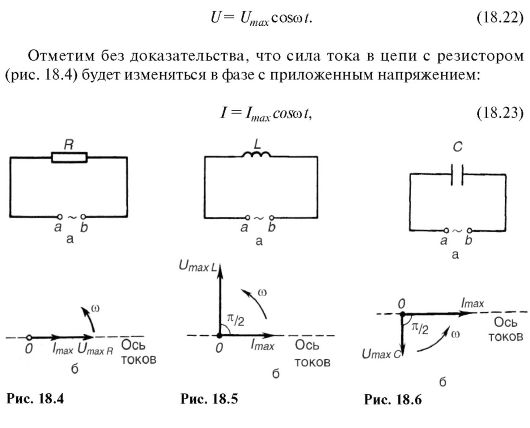
18.3. ПОЛНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА. РЕЗОНАНС НАПРЯЖЕНИЙ

Представим цепь, в которой последовательно соединены резистор, катушка индуктивности и конденсатор (рис. 18.7). Напряжение на зажимах a, b цепи, создаваемое внешним источником, выражается по-прежнему зависимостью (18.22) с амплитудой U_max.

В последовательной цепи сила тока на всех участках одинакова, а напряжения различны. Как видно из 14.2, в общем случае сила тока в цепи и напряжение изменяются не в одной фазе, поэтому

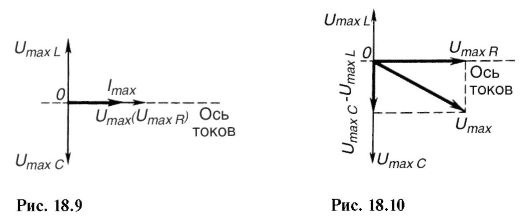
При этом условии полное сопротивление Z цепи имеет наименьшее значение, равное R (при данных R, L и С), а сила тока достигает наибольшего значения. Векторная диаграмма для резонанса напряжений в цепи показана на рис. 18.9. Если Lω >1/(Ссо), то tgcp >0 и φ >0, сила тока отстает по фазе от приложенного напряжения (см. рис. 18.8). При Leo <1/(Ссо) имеем tgcp <0 и φ <0. Сила тока опережает по фазе напряжение.

Векторная диаграмма для этого случая дана на рис. 18.10.

18.4. ПОЛНОЕ СОПРОТИВЛЕНИЕ (ИМПЕДАНС) ТКАНЕЙ ОРГАНИЗМА. ФИЗИЧЕСКИЕ ОСНОВЫ РЕОГРАФИИ

Ткани организма проводят не только постоянный, но и переменный ток. В организме нет таких систем, которые были бы подобны катушкам индуктивности, поэтому индуктивность его близка к нулю. Биологические мембраны и, следовательно, весь организм обладают емкостными свойствами, в связи с этим импеданс тканей организма определяется только омическим и емкостным сопротивлениями. Наличие в биологических системах емкостных элементов подтверждается тем, что сила тока опережает по фазе приложенное напряжение. Приведем некоторые значения угла сдвига фаз, полученные при частоте 1 кГц для разных биологических объектов (табл. 18.1).

Таблица 18.1

Омические и емкостные свойства биологических тканей можно моделировать, используя эквивалентные электрические схемы. Рассмотрим некоторые из них (рис. 18.11).

Для схемы, изображенной на рис. 18.11, а, частотная зависимость импеданса может быть получена из (18.36) при L = 0:

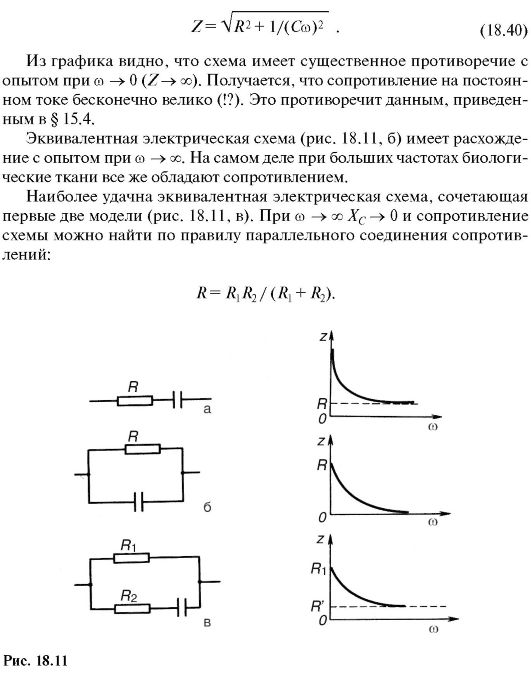
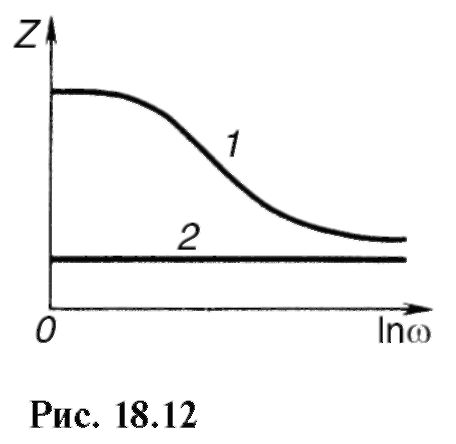
Частотная зависимость импеданса позволяет оценить жизнеспособность тканей организма, что важно знать для пересадки (трансплантации) тканей и органов. Проиллюстрируем это графически (рис. 18.12). Здесь 1 - кривая для здоровой, нормальной, ткани, 2 - для мертвой, убитой кипячением в воде. В мертвой ткани разрушены мембраны - «живые конденсаторы», и ткань обладает лишь омическим сопротивлением.

Различие в частотных зависимостях импенданса получается и в случаях здоровой и больной ткани.

Как видно из (18.38), угол сдвига фаз между током и напряжением также может давать информацию о емкостных свойствах ткани.

Импеданс тканей и органов зависит и от их физиологического состояния. Так, при кровенаполнении сосудов импеданс изменяется в зависимости от состояния сердечно-сосудистой деятельности.

Диагностический метод, основанный на регистрации изменения импеданса тканей в процессе сердечной деятельности, называют реографией (импеданс-плетизмография).

С помощью этого метода получают реограммы головного мозга (рео-энцефалограмма), сердца (реокардиограмма), магистральных сосудов, легких, печени и конечностей. Измерения обычно проводят на частоте 30 кГц.

18.5. ЭЛЕКТРИЧЕСКИЙ ИМПУЛЬС И ИМПУЛЬСНЫЙ ТОК

Электрическим импульсом назовем кратковременное изменение электрического напряжения или силы тока.

В технике импульсы подразделяются на две большие группы: видео-и радиоимпульсы.

Видеоимпульсы - это такие электрические импульсы тока или напряжения, которые имеют постоянную составляющую, отличную от нуля. Таким образом, видеоимпульс имеет преимущественно одну полярность. По форме видеоимпульсы бывают (рис. 18.13):

а) прямоугольные;

б) пилообразные;

в) трапецеидальные;

18.6. ПРОХОЖДЕНИЕ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ ЧЕРЕЗ ЛИНЕЙНУЮ ЦЕПЬ. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ЦЕПИ

При прохождении переменного тока через электрическую цепь, составленную из резисторов, катушек индуктивности и конденсаторов, сохраняется форма гармонического сигнала: данному внешнему гармоническому сигналу соответствует синусоидальный электрический ток. Таким образом, между силой тока и напряжением существует линейная зависимость и сама цепь называется линейной. Наличие таких элементов в цепи, как электронная лампа, полупроводниковый диод, транзистор, сделало бы цепь нелинейной.

Линейная цепь не искажает форму гармонического напряжения, но изменяет форму импульсного сигнала.

В практической медицине это важно иметь в виду по двум основным причинам.

Во-первых, снимая электрический сигнал для диагностических целей (см. 14.5) с биологического объекта, следует учитывать возможные искажения его формы в измерительной электрической цепи.

18.7. ПОНЯТИЕ О ТЕОРИИ МАКСВЕЛЛА. ТОК СМЕЩЕНИЯ

Обобщая результаты опытов Х.К. Эрстеда по воздействию электрического тока на магнитную стрелку, опытов Фарадея по электромагнитной индукции и других фактов, Максвелл создал в рамках классической физики теорию электромагнитного поля.

В основе теории Максвелла лежат два положения.

1. Всякое переменное электрическое поле порождает вихревое магнитное. Переменное электрическое поле было названо Максвеллом током смещения, так как оно, подобно обычному току, вызывает магнитное поле.

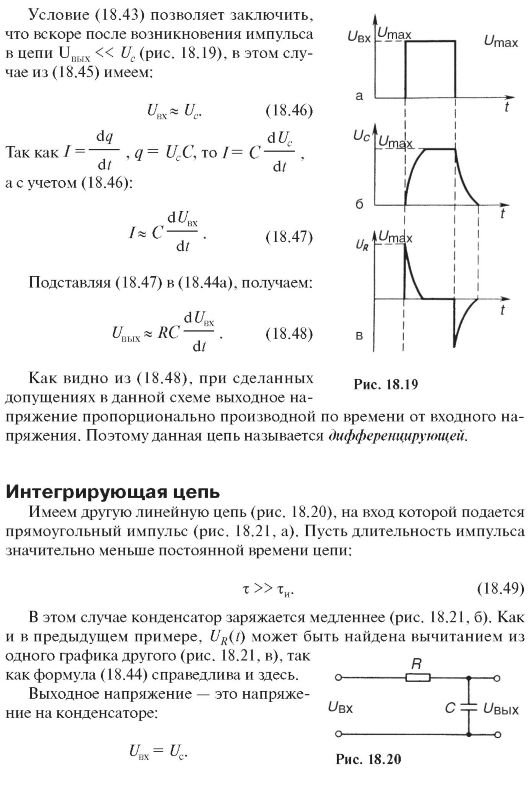
Чтобы найти выражение для силы тока смещения, рассмотрим прохождение переменного тока по цепи, в которую включен конденсатор с диэлектриком (рис. 18.22). Конденсатор не препятствует протеканию тока, что заметно по накалу лампочки. В проводниках это обычный ток проводимости 1_пр, обусловленный изменением заряда на обкладках конденсатора. Можно считать, что ток проводимости продолжается в конденсаторе током смещения 1_см, причем

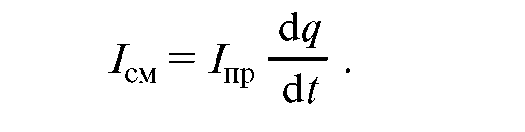
¹ А.А. Эйхенвальд был первым заведующим кафедрой физики Высших женских курсов в Москве, на основе которых был создан ряд московских вузов, в том числе и Российский медицинский университет.

В опыте Эйхенвальда диск из диэлектрика 1 (рис. 18.23) располагается между пластинами двух плоских конденсаторов 2 и 3. Напряженности электрического поля в них направлены противоположно. При вращении диска вокруг оси 4 происходит изменение поляризации диэлектрика в пространстве между конденсаторами. Это порождает магнитное поле, определяемое с помощью специальной индикаторной магнитной стрелки.

Подставляя выражение для силы тока смещения (18.51) в закон полного тока (16.46), получаем первое уравнение Максвелла:

которое связывает скорость изменения магнитного потока сквозь любую поверхность и циркуляцию вектора напряженности электрического поля, возникающего при этом. Циркуляция берется по контуру, на который опирается поверхность.

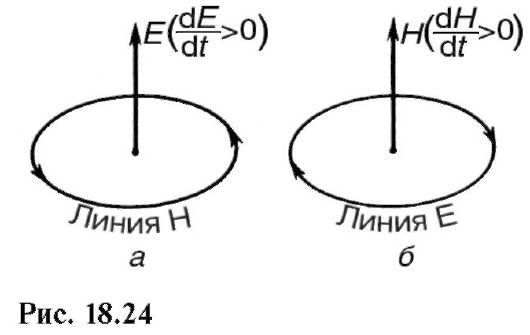
Из основных приведенных выше положений теории Максвелла следует, что возникновение какого-либо поля, электрического или магнитного, в некоторой точке пространства влечет за собой целую цепь взаимных превращений: переменное электрическое поле порождает магнитное (на рис. 18.24, а показаны Ε и линия напряженности возникшего магнитного поля при условии dE/dt > 0), изменение магнитного поля порождает электрическое (на рис, 18.24, б изображены Η и силовая линия возникшего электрического поля при условии dH/dt > 0) и т.д. Различие в знаке уравнений Максвелла (18.53) и (18.54) обусловливает различное направление стрелок на линиях Η и Ε этих рисунков.

18.8. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Взаимное образование электрических и магнитных полей приводит к понятию электромагнитной волны - распространение единого электромагнитного поля в пространстве.

Поясним это. Пусть в точке х₁ диэлектрика (рис. 18.25) возрастает напряженность Е₁ электрического поля. При этом возникает вихревое магнитное поле, напряженность которого Н₂ в точке х₂ направлена от читателя (ср. с рис. 18.24, а). Возрастание Н₂ вызывает вихревое электрическое поле, в точке х₂ вектор напряженности этого поля перпендикулярен оси ОХ (ср. с рис. 18.24, б) и т.д. Если изменения Ε или Н будут поддерживаться в заданной точке за счет энергии некоторого источника, то в пространстве будет непрерывно распространяться электромагнитная волна.

Покажем, что волновой характер распространения электромагнитного поля следует из уравнений Максвелла (18.53) и (18.54). Будем считать среду диэлектриком; следовательно, сила тока проводимости равна нулю. Магнитный поток через некоторую площадь S, расположенную перпендикулярно линиям В , равен:

¹ Уравнения Максвелла записаны в частных производных, так как в дальнейшем возникнет необходимость дифференцирования по координате.

Аналогичное уравнение можно получить и для напряженности магнитного поля:

18.9. ШКАЛА ЭЛЕКТРОМАГНИТНЫХ ВОЛН. КЛАССИФИКАЦИЯ ЧАСТОТНЫХ ИНТЕРВАЛОВ, ПРИНЯТАЯ В МЕДИЦИНЕ

Из теории Максвелла вытекает, что различные электромагнитные волны, в том числе и световые, имеют общую природу. В связи с этим целесообразно представить всевозможные электромагнитные волны в виде единой шкалы (рис. 18.27).

Вся шкала условно подразделена на шесть диапазонов: радиоволны (длинные, средние и короткие), инфракрасные, видимые, ультрафиоле-

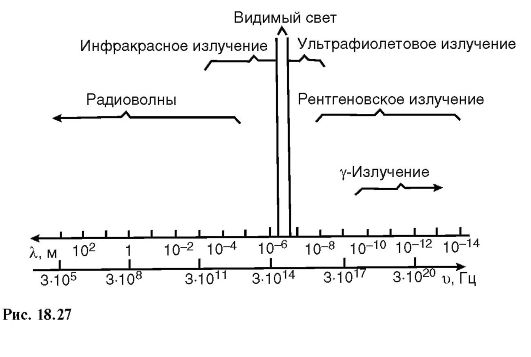
товые, рентгеновские и гамма-излучение. Эта классификация определяется либо механизмом образования волн, либо возможностью зрительного восприятия их человеком.

Радиоволны обусловлены переменными токами в проводниках и электронными потоками (макроизлучатели). Инфракрасное, видимое и ультрафиолетовое излучения исходят из атомов, молекул и быстрых заряженных частиц (микроизлучатели). Рентгеновское излучение возникает при внутриатомных процессах, γ-излучение имеет ядерное происхождение.

Некоторые диапазоны перекрываются, так как волны одной и той же длины могут образоваться в разных процессах. Так, наиболее коротковолновое ультрафиолетовое излучение перекрывается длинноволновым рентгеновским.

В этом отношении очень характерна пограничная область инфракрасных волн и радиоволн. До 1922 г. между этими диапазонами был пробел. Наиболее коротковолновое излучение этого незаполненного промежутка имело молекулярное атомное происхождение (излучение нагретого тела), а наиболее длинноволновое излучалось макроскопическими вибраторами Герца. Российским физиком А.А. Глаголевой-Аркадьевой¹ было предложено пропускать искру через смесь большого числа мелких металлических опилок в масле. При этом можно было получить различные электромагнитные волны с длиной волны 82 мкм и более. Диапазоны инфракрасных и радиоволн были сомкнуты.

Сейчас никого не удивляет, что даже миллиметровые волны могут генерироваться не только радиотехническими средствами, но и молекулярными переходами. Появился раздел - радиоспектроскопия, который изучает поглощение и излучение радиоволн различными веществами. В медицине принято следующее условное разделение электромагнитных колебаний на частотные диапазоны (табл. 18.2).

Таблица 18.2

¹ Александра Андреевна Глаголева-Аркадьева была первым заведующим кафедры физики 2-го Московского медицинского института (ныне Российский медицинский университет).

Окончание табл. 18.2

Часто физиотерапевтическую электронную аппаратуру низкой и звуковой частоты называют низкочастотной. Электронную аппаратуру всех других частот называют обобщающим понятием высокочастотная.