Глава 12. Термодинамика

Под термодинамикой понимают раздел физики, рассматривающий системы (термодинамические системы), между которыми возможен обмен энергией, без учета микроскопического строения тел, составляющих систему. Различают термодинамику равновесных систем или систем, переходящих к равновесию (классическая, или равновесная, термодинамика, часто называемая просто термодинамикой), и термодинамику неравновесных систем (неравновесная термодинамика). Неравновесная термодинамика играет особую роль для рассмотрения биологических систем. В главе наряду с термодинамикой освещены также вопросы, связанные с использованием низких температур и нагретых сред для лечения, и элементы термометрии и калориметрии.

12.1. ОСНОВНЫЕ ПОНЯТИЯ ТЕРМОДИНАМИКИ. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ

Состояние термодинамической системы характеризуется физическими величинами, называемыми параметрами (объем, давление, температура, плотность и т.д.).

Если параметры системы при взаимодействии ее с окружающими телами не изменяются с течением времени, то состояние системы называют стационарным. Примерами таких состояний в течение небольшого отрезка времени являются состояние внутренней части работающего домашнего холодильника, состояние тела человека, состояние воздуха в отапливаемом помещении и т.д.

В разных частях системы, находящейся в стационарном состоянии, значения параметров обычно различаются: температура в разных участках тела человека, концентрация диффундирующих молекул в разных частях биологической мембраны и т.п. В системе, таким образом, поддерживаются постоянные градиенты некоторых параметров, с постоянной скоростью могут протекать химические реакции.

Стационарное состояние поддерживается за счет потоков энергии и вещества, проходящих через систему. Схематически на рис. 12.1, а показано стационарное состояние, температура неодинакова в разных точках системы (1 и 2). Ясно, что в стационарном состоянии могут на-

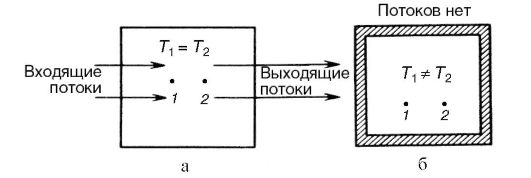
Рис. 12.1

ходиться такие системы, которые либо обмениваются и энергией и веществом с окружающими системами (открытые системы), либо, по крайней мере, обмениваются только энергией (закрытые системы).

Термодинамическая система, которая не обменивается с окружающими телами ни энергией, ни веществом, называется изолированной. Изолированная система со временем приходит в состояние термодинамического равновесия. В этом состоянии, как и в стационарном, параметры системы сохраняются неизменными во времени. Однако существенно, что в равновесном состоянии параметры, не зависящие от массы или числа частиц (давление, температура и др.), одинаковы в разных частях этой системы.

Естественно, что любая реальная термодинамическая система не будет изолированной хотя бы потому, что ее невозможно окружить оболочкой, не проводящей теплоту. Изолированную систему можно рассматривать как удобную термодинамическую модель. Схематически равновесное состояние изолированной системы показано на рис. 12.1, б.

Рассмотрим подробнее взаимодействие закрытой системы с окружающими телами. Обмен энергией между ними может осуществляться в двух различных процессах: при совершении работы и при теплообмене.

Мерой передачи энергии в процессе теплообмена является количество теплоты, а мерой передачи энергии в процессе работы является работа¹.

Найдем выражение для вычисления работы, совершаемой газом при изменении его объема. Предположим, что газ, находящийся в цилиндрическом сосуде под поршнем, изобарно расширяется от V₁ до V₂ (рис. 12.2), при этом поршень перемещается на расстояние Δ/ = l₂ - l₁, а объем изменяется на ΔΥ = V₂ - V₁.

¹ Не вполне удачно, что работой называют и один из возможных процессов передачи энергии, и меру передачи энергии в этом процессе.

12.2. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ЭНТРОПИЯ

Первое начало термодинамики, являющееся законом сохранения энергии, не указывает направления возможного протекания процессов. Так, например, по первому началу термодинамики, при теплообмене одинаково возможным был бы как самопроизвольный переход теплоты от тела более нагретого к телу менее нагретому, так и, наоборот, от тела менее нагретого к телу более нагретому. Из повседневного опыта, однако, хорошо известно, что второй процесс в природе нереален; так, например, не может самопроизвольно нагреться вода в чайнике вследствие охлаждения воздуха в комнате.

Другой пример: при падении камня на Землю происходит его нагревание, эквивалентное изменению потенциальной энергии, обратный процесс - самопроизвольное поднятие камня только из-за его охлаждения - невозможен.

Второе начало термодинамики, так же как и первое, является обобщением данных опыта.

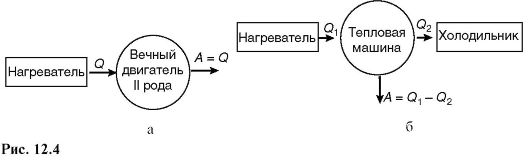
Существует несколько формулировок второго закона термодинамики: теплота сама собой не может переходить от тела с меньшей температурой к телу с большей температурой (формулировка Клаузиуса), или невозможен вечный двигатель второго рода (формулировка Томсона), т.е. такой периодический процесс, единственным результатом которого было бы превращение теплоты в работу вследствие охлаждения одного тела.

В тепловой машине совершается работа за счет теплоты, полученной от нагревателя, но при этом часть теплоты обязательно передается холодильнику. На рис. 12.4 схематически показаны соответственно невозможный (а) и возможный (б), по второму началу, периодические процессы.

Рассмотрим некоторые термодинамические понятия, которые позволяют количественно выразить второе начало термодинамики.

Процесс 1-2 называют обратимым, если можно совершить обратный процесс 2-1 через все промежуточные состояния так, чтобы после возвращения системы в исходное состояние в окружающих телах не произошло каких-либо изменений.

Обратимый процесс является физической абстракцией. Все реальные процессы необратимы хотя бы из-за наличия силы трения, которая вызывает нагревание окружающих тел. Некоторые характерные примеры необратимых процессов: расширение газа в пустоту, диффузия, теплообмен т.д. Для возвращения системы в начальное состояние во всех этих случаях необходимо совершение работы внешними телами.

Циклом или круговым процессом называют процесс, при котором система возвращается в исходное состояние.

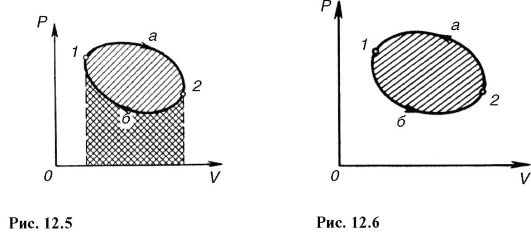
График цикла представляет собой замкнутую линию. Цикл, изображенный на рис. 12.5, прямой, он соответствует тепловой машине, т.е. устройству, которое получает количество теплоты Q₁ от некоторого тела - теплоотдатчика (нагревателя), совершает работу и отдает часть этой теплоты другому Q₂ телу - теплоприемнику (холодильнику) (рис. 12.4).

В этом цикле рабочее вещество (газ) совершает положительную работу (рис. 12.5): в процессе 1-а-2 газ расширяется, работа положительна и численно равна площади под кривой 1-а-2; в процессе 2-6-1 работа отрицательна (сжатие газа) и по модулю равна площади под соответствующей кривой. Алгебраическое суммирование дает в целом положительную работу, совершенную газом за цикл и численно равную по модулю площади, ограниченной замкнутой кривой 1-а-2- 6-1.

Обратный цикл¹ соответствует работе холодильной машины, т.е. такой системе, которая отбирает теплоту от холодильника и передает

¹ Не следует путать обратный цикл с обратимым. Обратимый цикл состоит из обратимых процессов, он может быть как прямой (тепловая машина), так и обратный (холодильная машина).

большее количество теплоты нагревателю. Как следует из второго закона термодинамики, этот процесс (рис. 12.6) не может протекать сам собой, он происходит за счет работы внешних тел. При этом газ совершает отрицательную работу: работа сжатия в процессе 2-а-1 отрицательна, работа расширения в процессе 1-6-2 положительна. В результате алгебраического суммирования получаем отрицательную работу газа, равную по модулю площади, ограниченной кривой 2-а-1-6-2.

Коэффициентом полезного действия тепловой машины или прямого цикла называют отношение совершенной работы к количеству теплоты, полученномурабочим веществом от нагревателя:

Рассмотрим цикл Карно (рис. 12.7), состоящий из двух изотерм 1-2, 3-4, которым соответствуют температуры T₁ и T₂ (T₁ > Г₂), и двух адиабат - 2-3, 4-1. В этом цикле рабочим веществом является идеальный газ. Передача количества теплоты от нагревателя рабочему веществу происходит при температуре T₁, а от рабочего вещества к холодильнику - при температуре T₂. Без доказательства укажем, что к.п.д. обратимого цикла Карно зависит только от температур T₁ и Г₂ нагревателя и холодильника:

Последнее означает, что сумма приведенных количеств теплоты при обратимом переходе системы из одного состояния в другое не зависит от процесса, а для данной массы газа определяется только начальным и конечным состояниями системы. На рис. 12.9 показаны графики различных обратимых процессов (а, б, в), общими для которых являются начальное 1 и конечное 2 состояния. Количества теплоты и работы в этих процессах различны, но сумма приведенных количеств теплоты одинакова.

Физическую характеристику, не зависящую от процесса или перемещения, обычно выражают как разность двух значений некоторой функции, соответствующих конечному и начальному состояниям процесса или положениям системы. Так, например, независимость работы силы тяжести от траектории позволяет выразить эту работу через разность потенциальных энергий в конечных точках траектории; независимость работы сил электростатического поля от траекторий заряда позволяет связать эту работу с разностью потенциалов точек поля, являющихся граничными при его перемещении. Аналогично, сумму приведенных количеств теплоты для обратимого процесса можно представить как разность двух значений некоторой функции состояния системы, которую называют энтропией:

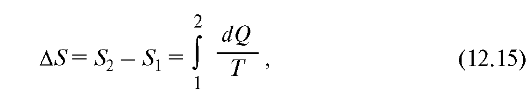
где S₂ и S₁ - энтропия соответственно в конечном 2 и начальном 1 состояниях. Итак, энтропия есть функция состояния системы, разность значений которой для двух состояний равна сумме приведенных количеств теплоты при обратимом переходе системы из одного состояния в другое.

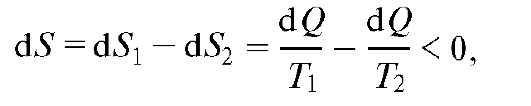
а это противоречит (12.18). Таким образом, в изолированной системе не могут протекать такие процессы, которые приводят к уменьшению энтропии системы (второе начало термодинамики).

Увеличение энтропии в изолированной системе не будет происходить беспредельно. В рассмотренном выше примере температуры тел со временем выравняются, теплопередача между ними прекратится и наступит равновесное состояние (см. 12.1). В этом состоянии параметры системы будут оставаться неизменными, а энтропия достигнет максимума.

Согласно молекулярно-кинетической теории, энтропию наиболее удачно можно охарактеризовать как меру неупорядоченности частиц системы. Так, например, при уменьшении объема газа его молекулы вынуждены занимать все более определенные положения одна относительно другой, что соответствует большему порядку в системе, при этом энтропия убывает. Когда газ конденсируется или жидкость кристаллизуется при постоянной температуре, то выделяется теплота, энтропия убывает, а упорядоченность в расположении частиц - возрастает.

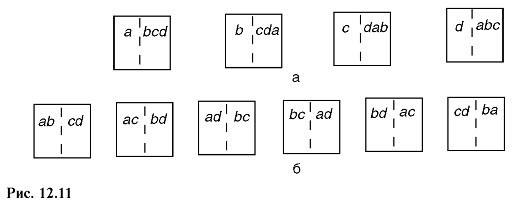
Неупорядоченность системы количественно характеризуется термодинамической вероятностью ^_тер. Для выяснения ее смысла рассмотрим систему, состоящую из четырех частиц газа: а, b, с, d (рис. 12.11). Эти частицы находятся в объеме, мысленно разделенном на две равные ячейки, и могут свободно в нем перемещаться.

Состояние системы, определяемое числом частиц в первой и второй ячейках, назовем макросостоянием; состояние системы, определяемое тем, какие конкретно частицы находятся в каждой из ячеек, - микросостоянием. Тогда (рис. 12.11, а) макросостояние - одна частица в первой ячейке и три частицы во второй - осуществляется четырьмя микросо-

12.3. КРИТИКА ТЕОРИИ «ТЕПЛОВОЙ СМЕРТИ» МИРА

Настоящий параграф писался в период господства марксистко-ленинской философии. С позиции современной физики он абсолютно несостоятелен и сохранен как пример курьезов, возникающих при внедрении идеалогии в науку.

Клаузиус, а вслед за ним и некоторые другие ученые положение о возрастании энтропии изолированной системы перенесли на всю Вселенную, утверждая, что энтропия мира стремится к максимуму. При достижении максимума все виды энергии перейдут в молекулярно-кинетическую энергию, станут равными температуры, концентрации и т.п., прекратятся биологические процессы, наступит «тепловая смерть» мира.

Теория «тепловой смерти» мира с момента своего создания была подвергнута критике как учеными-естествоиспытателями, так и философами, которые показали ее несостоятельность и как физической теории, и как философской концепции.

Прежде всего нельзя выводы, полученные для изолированной системы, переносить на всю Вселенную, ибо изолированность уже предполагает ограниченность и наличие каких-то тел вне системы, в то время как Вселенная безгранична. Больцман опровергал выводы Клаузиуса о неизбежности «тепловой смерти» мира, считая, что так как Вселенная состоит из огромного числа частиц, то в ней принципиально возможны случаи, когда в отдельных частях возникнут колоссальные флуктуации (неоднородности). И действительно, данные астрофизики свидетельствуют, что и сейчас рождаются новые звезды из распыленной материи, т.е. происходят концентрации энергии. Это подтверждает, что второй закон термодинамики, как уже отмечалось, не применим к явлениям в масштабе Вселенной.

Согласно современным представлениям, однородное распределение вещества с одинаковой температурой не является наиболее вероятным и не соответствует максимуму энтропии, если учитывать наличие тяготения.

Вселенная нестационарна, она расширяется, под действием сил тяготения возрастает неоднородность вещества, возникают галактики, звезды, планеты. При наличии тяготения этому естественному процессу соответствует рост энтропии.

Из теории «тепловой смерти» возникает и такой вопрос: если мир когда-нибудь придет к «тепловой смерти», то почему он не пришел к ней раньше? Отсюда можно заключить, что мир существовал не вечно, а когда-то возник и когда-то умрет. И тогда можно говорить о каком-то творце мироздания, что непосредственно ведет к религиозным воззрениям. Поэтому неудивительно, что и в наше время духовенство поддерживает идею «тепловой смерти» мира.

12.4. ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ

При решении разнообразных термодинамических задач аналитическим методом используют особые функции - термодинамические потенциалы. Зная выражение термодинамических потенциалов, через независимые параметры системы можно вычислить остальные параметры и иные характеристики термодинамических процессов.

Рассмотрим некоторые из термодинамических потенциалов.

Подставим в формулу первого закона термодинамики (12.7) выражение для работы (12.2) и количества теплоты в обратимом процессе (dQ = TdS):

Используя выражение для d U[cm. (12.21)], преобразуем (12.24):

и для дифференциала энергии Гиббса вместо равенства (12.29) получаем следующее неравенство:

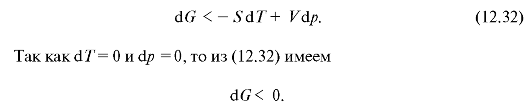
Такое уменьшение энергии Гиббса будет происходить до тех пор, пока не установится равновесное состояние, и изменение энергии Гиббса станет равным нулю (dG = 0). Таким образом, в изобарно-изотермиче-ском неравновесном процессе энергия Гиббса убывает и в состоянии термодинамического равновесия минимальна.

Аналогично в состоянии термодинамического равновесия ведут себя другие термодинамические потенциалы (U, F и др.).

Так, например, убывает при приближении к равновесию и минимальна F = F_min в состоянии равновесия энергия Гельмгольца для изотермической системы с постоянным объемом, т.е. в случае dT = 0 и dV = 0.

12.5. СИСТЕМЫ С ПЕРЕМЕННЫМ ЧИСЛОМ ЧАСТИЦ. ХИМИЧЕСКИЙ И ЭЛЕКТРОХИМИЧЕСКИЙ

ПОТЕНЦИАЛЫ

Изложенное выше относилось к случаю, когда количество вещества в системе оставалось неизменным. Однако в термодинамике изучаются также и системы, в которых изменяется число частиц. В этом случае изменение внутренней энергии системы обусловлено не только теплообменом (dQ=TdS) и совершением работы (d^ = pdV), но и изменением числа частиц в системе. Поэтому вместо уравнения (12.21) следует записать следующее:

Здесь dN - изменение числа частиц в системе, a μ - коэффициент, называемый химическим потенциалом. Если в дифференциалы энергии Гельмгольца и энергии Гиббса подставить полный дифференциал внутренней энергии не в виде (12.21), а в записи (12.33), то получим соответственно:

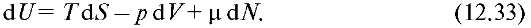
12.6. СТАЦИОНАРНОЕ СОСТОЯНИЕ. ПРИНЦИП МИНИМУМА ПРОИЗВОДСТВА ЭНТРОПИИ

Изложенные выше вопросы термодинамики относились в основном к равновесным процессам или к процессам, которые приводят к равновесным состояниям. Такие ограничения позволили объяснить направленность термодинамических процессов в изолированной системе.

Реальные процессы и состояния в природе и технике являются неравновесными, а многие системы - открытыми. Эти процессы и системы рассматриваются в неравновесной термодинамике.

Аналогично тому, как в равновесной термодинамике особым состоянием является состояние равновесия, так в неравновесной термодинамике особую роль играют стационарные состояния.

Несмотря на то что в стационарном состоянии необратимые процессы, протекающие в системе (диффузия, теплопроводность и др.), увеличивают энтропию, энтропия системы не изменяется. Как понять это противоречие?

Представим изменение энтропии ΔS системы в виде суммы двух слагаемых:

ΔS = ΔS_i+ ΔS_e, (12.41)

где ΔS_i - изменение энтропии, обусловленное необратимыми процессами в системе; ΔS_e - изменение энтропии, вызванное взаимодействием системы с внешними телами (потоки, проходящие через систему).

Необратимость процессов приводит к ΔS_i > 0, стационарность состояния - к ΔS = 0; следовательно, ΔS_e = ΔS - ΔS_i < 0. Это означает, что энтропия в продуктах (вещество и энергия), поступающих в систему, меньше энтропии в продуктах, выходящих из системы.

В равновесном состоянии, как уже отмечалось, энтропия максимальна, а энергия Гиббса минимальна. Для стационарных состояний И. При-гожин также указал экстремальное значение некоторой функции, сформулировав принцип минимума производства энтропии: в стационарном состоянии системы скорость возникновения энтропии вследствие необратимых процессов имеет минимальное значение при данных внешних условиях, препятствующих достижению системой равновесного состояния (dS_i /dt > 0 и минимальна).

Согласно принципу Пригожина, в системе при стационарном состоянии внутренние неравновесные процессы (диффузия), теплопроводность, химические реакции и др.) протекают так, что ежесекундный

прирост энтропии минимален. Это означает, что система за счет внутренних необратимых процессов не способна выйти из стационарного состояния. Так, если за счет небольших отклонений (флуктуации) система несколько и отклонилась бы от стационарного состояния, то стремление внутренних процессов уменьшить dS₍- /dt вернет систему вновь к этому состоянию.

Отметим, что все изложенное, в том числе и принцип Пригожина, справедливо при заданных и неизменных внешних условиях. При изменении внешнего воздействия (потоков, входящих и исходящих из системы) система уходит из одного стационарного состояния и переходит в другое в том случае, если новые внешние условия будут сохраняться во времени.

Примерами переходных процессов между стационарными состояниями в биологических системах являются генерация нервного импульса, мышечное сокращение и др.

Термодинамические потенциалы системы в стационарном состоянии не изменяются. Воспользуемся условием постоянства энергии Гиббса для установления связи между электрическим напряжением на биологической мембране и концентрацией ионов по обе стороны от нее.

¹ Здесь индекс i образован от inside - внутри; не следует его смешивать с обозначением i-го компонента.

циклов и термодинамических потенциалов применительно к идеализированным процессам: равновесным и обратимым.

Термодинамика биологических систем в этот период не развивалась. Ярким исключением из этого была работа Майера, который по цвету венозной крови матросов, работающих в условиях тропического климата, сформулировал, по существу, приложимость закона сохранения энергии (первый закон термодинамики) к живым системам.

Первый закон термодинамики как закон сохранения энергии настолько общепонятен, что его применения к биологическим системам здесь не рассматриваются, тем более что в курсе нормальной физиологии изучаются такие темы, как «Обмен веществ и энергии. Питание. Терморегуляция!», а в 27.5 анализируется теплообмен человека с окружающей средой тепловым излучением. Более существенно рассмотреть некоторые вопросы, связанные со вторым началом термодинамики (энтропией) и биологическими системами.

Биологические объекты являются открытыми термодинамическими системами. Они обмениваются с окружающей средой энергией и веществом.

Вообще говоря, живой организм - развивающаяся система, которая не находится в стационарном состоянии. Однако обычно в каком-либо не слишком большом интервале времени принимают состояние биологической системы за стационарное.

Рассмотрим в этом предположении некоторые вопросы. Для организма - стационарной системы - можно записать (см. 12.6) dS = 0, S = const, dS_t > 0, dS_e < 0. Это означает, что большая энтропия должна быть в продуктах выделения, а не в продуктах питания. Энтропия системы организм-окружающая среда возрастает, как у изолированной системы, однако энтропия организма при этом сохраняется постоянной. Энтропия есть мера неупорядоченности системы (см. 12.2), поэтому можно заключить, что упорядоченность организма сохраняется ценой уменьшения упорядоченности окружающей среды.

При некоторых патологических состояниях энтропия биологической системы может возрастать (dS > 0), это связано с отсутствием стационарности, увеличением неупорядоченности; так, например, при раковых заболеваниях происходит хаотическое, неупорядоченное разрастание клеток.

Формулу (12.41) можно преобразовать к виду

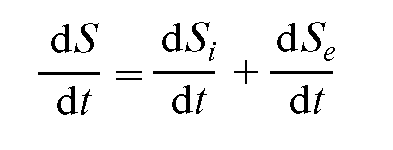
Основа функционирования живых систем (клетки, органы, организм) - это поддержание стационарного состояния при условии протекания диффузионных процессов, биохимических реакций, осмотических явлений и т.п.

При изменении внешних условий процессы в организме развиваются так, что его состояние не будет прежним стационарным состоянием.

Можно указать некоторый термодинамический критерий приспособления организмов и биологических структур к изменениям внешних условий (адаптация). Если внешние условия изменяются (возрастает или уменьшается температура, изменяется влажность, состав окружающего воздуха и т.д.), но при этом организм (клетки) способен поддерживать стационарные состояния, то организм адаптируется (приспосабливается) к этим изменениям и существует. Если организм при изменении внешних условий не способен сохранить стационарное состояние, уходит от этого состояния, то это приводит к его гибели. Организм в этом случае не смог адаптироваться, т.е. не смог сравнительно быстро оказаться в стационарном состоянии, соответствующем изменившимся условиям.

И последнее. Приведенные в параграфе рассуждения основываются на том, что организм - стационарная система, не слишком далеко отстоящая от состояния равновесия. В этом случае справедлив принцип Пригожина. Живые организмы далеко отстоят от положения равновесия. Поэтому в рамках сделанных допущений невозможно объяснить, в частности, рост клеток и возникновение новых структур. В сильно неравновесной системе необходимо учитывать принцип Пригожина-Глансдорфа, согласно которому скорость производства энтропии уменьшается.

В этой области неравновесная термодинамика смыкается с синергетикой, однако рассмотрение подобных вопросов выходит за пределы курса.

12.8. ТЕРМОМЕТРИЯ И КАЛОРИМЕТРИЯ

Точные измерения температур являются неотъемлемой частью научно-исследовательских и технических работ, а также медицинской диагностики и биологии.

Диапазон известных температур очень широк. Самая низкая температура, полученная к настоящему времени, - около 2?10^-5 К. Верхний предел достижимых температур ничем не ограничен. Наибольшая температура достигнута в земных условиях при взрыве водородной бомбы и составляет примерно 10⁸ К.

В недрах звезд, по спектроскопическим данным, температура может достигать 10⁹ К и более.

Температурный интервал окружающей среды, в которой могут длительно или кратковременно находиться биологические системы, сохраняя способность к функционированию, значительно уже. И совсем невелик (приблизительно от 0 до 90 °С) диапазон температур самих живых организмов в состоянии их активной жизнедеятельности.

Методы получения и измерения температур в широком диапазоне весьма различны. Область прикладной физики, в которой изучаются методы измерения температуры и связанные с этим вопросы, называют термометрией.

Как известно, температура не может быть измерена непосредственно. Для ее определения нужно установить температурную шкалу: выбрать термометрическое вещество и физическое свойство, зависящее от температуры (термометрическое свойство), условиться о начальной точке отсчета и единице температуры. Для этого обычно выбирают две основные температуры (реперные точки), соответствующие температурам фазовых переходов, например плавлению льда и кипению воды при определенных внешних условиях. Участок шкалы между этими точками называют основным интервалом. За начало отсчета принимают одну из реперных точек (например, 0 °С - температура таяния льда), за единицу температуры - долю основного интервала. Так, 1 °С составляет 0,01 доли основного интервала.

Температурные шкалы различаются по термометрическому свойству или веществу. Можно построить огромное количество шкал, значитель-

но отличающихся одна от другой, так как ни одно из свойств не зависит от температуры строго линейно и, кроме того, определяется природой вещества.

Принципиальным недостатком всех эмпирических шкал является их зависимость от свойств термометрического вещества. Независимая от свойств и вещества шкала построена на основе второго начала термодинамики и названа термодинамической шкалой температур. За репер-ную точку ее принята температура тройной точки воды 273,16 К. Определяется эта шкала с помощью цикла Карно. Измерив количество теплоты Q₀ и Q_s в изотермических процессах этого цикла соответственно при температуре T₀ таяния льда и T_s кипения воды, можно найти

T/T = Qs/Q0. Аналогично, для произвольной температуры Т

T/T = Q/Q0,

где Q - количество теплоты, сообщенное системе в изотермическом процессе при температуре Т. Установленную таким образом температуру называют термодинамической.

Единицей термодинамической температуры является кельвин (К) - 1/273,16 термодинамической температуры тройной точки воды. Кельвин как единица температурного интервала равен 1/273,16 интервала термодинамической температуры между 0 К и тройной точкой воды.

Любая эмпирическая шкала приводится к термодинамической посредством введения поправок, учитывающих зависимость термического свойства данного вещества от температуры.

Так как температура определяется по значению какой-либо характеристики термодинамического вещества, то ее определение состоит в измерении таких физических параметров и свойств, как объем, давление, электрические, механические, оптические, магнитные и т.п. Разнообразие методов измерения температуры связано с большим количеством термометрических веществ и свойств, используемых при этом.

Термометры - устройства для измерения температуры - состоят из чувствительного элемента, в котором реализуется термометрическое свойство, и измерительного прибора (дилатометр, манометр, гальванометр, потенциометр и т.д.). Необходимое условие измерения температуры - тепловое равновесие чувствительного элемента и тела, температура которого определяется.

В зависимости от измеряемых интервалов температур наиболее распространены жидкостный, газовый термометры, термометр сопротивления, термопара как термометр и пирометры.

В жидкостном термометре термометрической характеристикой является объем, чувствительным элементом - резервуар с жидкостью (обычно ртуть или спирт). В пирометрах в качестве термометрического свойства используется интенсивность излучения. Принципиальное отличие пирометров от других термометров состоит в том, что их чувствительные элементы не находятся в непосредственном контакте с телом. Пирометры применяют для измерения сколь угодно высоких температур.

При измерении сверхнизких температур термометрическим веществом служат парамагнетики, а измеряемым свойством - зависимость их намагниченности от температуры.

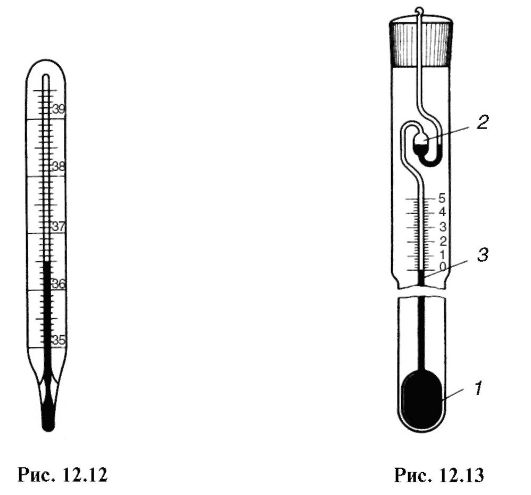
Используемый в медицине ртутный термометр указывает максимальную температуру и называется максимальным термометром. Эта особенность обусловлена его устройством: резервуар с ртутью отделен от градуированного капилляра волосяным сужением, которое не позволяет ртути при охлаждении термометра возвратиться в резервуар (рис. 12.12). Существуют и минимальные термометры, показывающие наименьшую температуру, наблюдаемую за длительный промежуток времени.

Для измерения температуры с большой точностью в небольшом интервале значений служит метастатический термометр (рис. 12.13), состоящий из большого резервуара 1 с жидкостью (обычно ртуть) и узкого длинного капилляра 3. Масса ртути в резервуаре 1 переменна, часть ее может быть перелита в резервуар 2, в результате чего на отметке шкалы 0 установлен нижний предел измеряемого интервала температуры. Цена деления такого термометра равна 0,01°. Интервал отсчета составляет всего 5°, но он может быть выбран около разных температур.

Многие процессы в физике, химии и биологии существенно зависят от температуры, поэтому получение и поддержание определенной температуры является важной задачей. Для этой цели служат термостаты - приборы, в которых температура поддерживается постоянной, что осуществляют либо автоматическими регуляторами, либо используют для этого свойство фазовых переходов протекать при неизменной температуре.

Для измерения количества теплоты, выделяющегося или поглощаемого в различных физических, химических и биологических процессах, применяют ряд методов, совокупность которых составляет калориметрию¹.

¹ Группу методов измерения тепловых эффектов, сопровождающих процессы жизнедеятельности, называют также биокалориметрией, а соответствующие приборы - биокалориметрами.

Калориметрическими методами измеряют теплоемкость тел, теплоты фазовых переходов, растворения, смачивания, адсорбции, теплоты, сопровождающие химические реакции, энергию излучения, радиоактивного распада и т.п.

Подобные измерения производят с помощью калориметров. Эти приборы можно разделить на два основных типа: калориметры, в которых количество теплоты определяют по изменению их температуры, и калориметры, у которых температура постоянна и количество теплоты определяют по количеству вещества, перешедшего в другое фазовое состояние (например, плавящееся твердое тело).

Большинство практически используемых калориметров относится к первому типу. В этих случаях количество теплоты, полученное системой калориметр-исследуемое тело, можно найти по формуле:

где с_к - теплоемкость калориметрической системы; Δ Τ - изменение ее температуры, которое наблюдалось бы при отсутствии теплообмена с окружающими телами.

Для определения Δ Т в измеренное на опыте изменение температуры должна быть внесена поправка, учитывающая теплообмен с окружаю-

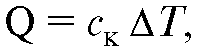
щей средой. В этом отношении все калориметры можно разделить на калориметры с изотермической и адиабатной оболочками. Для поддержания изотермических или адиабатных условий калориметр снабжают регуляторами температуры, в качестве которых чаще всего используют контактные термометры, а также термометры сопротивления и дифференциаль-

ные термопары.

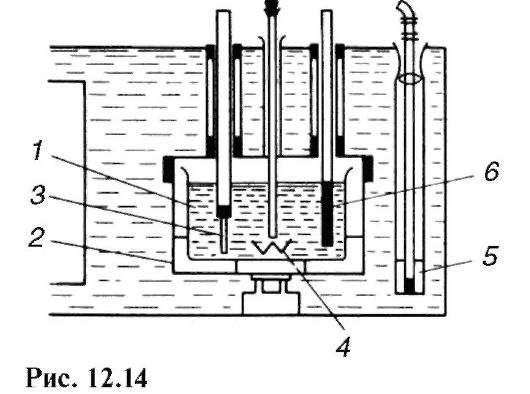
На рис. 12.14 приведена схема простейшего жидкостного калориметра: 1 - калориметрический сосуд; 2 - цилиндрический сосуд-оболочка; 3 - нагреватель; 4 и 5 - мешалки; 6 - термометр.

Калориметры могут служить и термостатами.

12.9. ФИЗИЧЕСКИЕ СВОЙСТВА НАГРЕТЫХ И ХОЛОДНЫХ СРЕД, ИСПОЛЬЗУЕМЫХ ДЛЯ ЛЕЧЕНИЯ. ПРИМЕНЕНИЕ НИЗКИХ ТЕМПЕРАТУР В МЕДИЦИНЕ

В медицине с целью местного нагревания или охлаждения применяют нагретые или холодные тела.

Обычно для этого выбирают сравнительно доступные среды, некоторые из них могут оказывать при этом полезное механическое или химическое действие.

Физические свойства таких сред обусловливаются их назначением. Во-первых, необходимо, чтобы в течение сравнительно длительного времени был произведен нужный эффект. Поэтому используемые среды должны иметь большую удельную теплоемкость (вода, грязи) или удельную теплоту фазового превращения (парафин, лед). Во-вторых, среды, накладываемые непосредственно на кожу, не должны вызывать болезненных ощущений. Это, с одной стороны, ограничивает температуру таких сред, а с другой - побуждает выбирать среды с небольшой теплоемкостью. Так, например, вода, применяемая для лечения, имеет температуру до 45 °С, а торф и грязи - до 50 °С, так как теплообмен (конвекция) в этих средах меньше, чем в воде. Парафин нагревают до 60-70 °С, так как он обладает небольшой теплопроводностью, а части

парафина, непосредственно прилегающие к коже, быстро остывают, кристаллизуются и задерживают приток теплоты от остальных его частей.

В качестве охлаждающей среды, используемой для лечения, употребляется лед.

В последние годы достаточно широкое применение в медицине нашли низкие температуры.

При низкой температуре осуществляют такую консервацию отдельных органов и тканей в связи с трансплантацией, когда достаточно долго сохраняется способность к жизнедеятельности и нормальному функционированию.

Криогенный¹ метод разрушения ткани при замораживании и размораживании используется медиками для удаления миндалин, бородавок т.п. Для этой цепи создают специальные криогенные аппараты и крио-зонды.

С помощью холода, обладающего анестезирующим свойством, можно уничтожить в головном мозгу человека клетки ядер, ответственные за некоторые заболевания, например паркинсонизм.

В микрохирургии используют примерзание («прилипание») влажных тканей к холодному металлическому инструменту для захвата и переноса этих тканей.

В связи с медицинскими применениями низкой температуры появились новые термины: «криогенная медицина», «криотерапия», «криохирургия» и т.д.

¹ Крио... - часть сложных слов, означающая связь со льдом, низкими температурами; криогенный - относящийся к низким температурам.