Глава 9. Течение и свойства жидкостей

К жидкостям относят вещества, которые по своим свойствам занимают промежуточное положение между газами и твердыми телами. Жидкие среды составляют наибольшую часть организма, их перемещение обеспечивает обмен веществ и снабжение клеток кислородом, поэтому механические свойства и течение жидкостей представляют особый интерес для медиков и биологов.

Материал, изложенный в главе, имеет отношение к гидродинамике - разделу физики, в котором изучают вопросы движения несжимаемых жидкостей и взаимодействие их при этом с окружающими твердыми телами, и к реологии - учению о деформациях и текучести вещества.

НЬЮТОНОВСКИЕ И НЕНЬЮТОНОВСКИЕ ЖИДКОСТИ

При течении реальной жидкости отдельные слои ее воздействуют друг на друга с силами, касательными к слоям. Это явление называют внутренним трением или вязкостью.

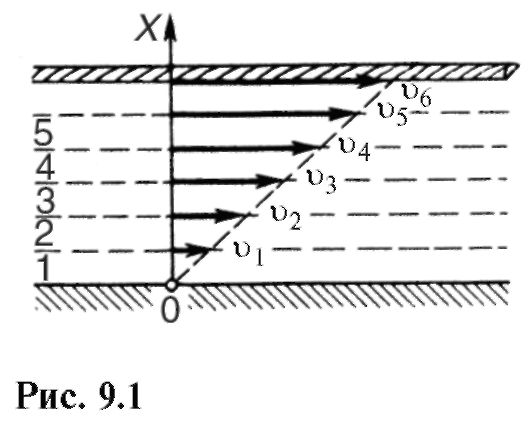
Рассмотрим течение вязкой жидкости между двумя твердыми пластинками (рис. 9.1), из которых нижняя неподвижна, а верхняя движется со скоростью υ_Β. Условно представим жидкость в виде нескольких слоев 1, 2, 3 и т.д. Слой, «прилипший» ко дну, неподвижен. По мере удаления от дна (нижняя пластинка) слои жидкости имеют все большие скорости (υ₁< υ₂< υ₃ <... и т.д), максимальная скорость υ_Β будет у слоя, который «прилип» к верхней пластинке.

9.1. ВЯЗКОСТЬ ЖИДКОСТИ.

УРАВНЕНИЕ НЬЮТОНА.

Слои воздействуют друг на друга. Так, например, третий слой стремится ускорить движение второго, но сам испытывает торможение с его стороны, а ускоряется четвертым слоем и т.д. Сила внутреннего трения пропорциональна площади S взаимодействующих слоев и тем больше, чем больше их относительная скорость.

Это уравнение Ньютона. Здесь η - коэффициент пропорциональности, называемый коэффициентом внутреннего трения или динамической с вязкостью (или просто вязкостью). Вязкость зависит от состояния и молекулярных свойств жидкости (или газа).

Единицей вязкости является паскаль-секунда (Пах). В системе СГС вязкость выражают в пуазах (П): 1 Пах = 10 П.

Для многих жидкостей вязкость не зависит от градиента скорости, такие жидкости подчиняются уравнению Ньютона (9.1) и их называют ньютоновскими. Жидкости, не подчиняющиеся уравнению (9.1), относят к неньютоновским. Иногда вязкость ньютоновских жидкостей называют нормальной, а неньютоновской - аномальной.

Жидкости, состоящие из сложных и крупных молекул, например растворы полимеров, и образующие благодаря сцеплению молекул или частиц пространственные структуры, являются неньютоновскими. Их вязкость при прочих равных условиях много больше, чем у простых жидкостей.

Увеличение вязкости происходит потому, что при течении этих жидкостей работа внешней силы затрачивается не только на преодоление истинной, ньютоновской, вязкости, но и на разрушение структуры. Кровь является неньютоновской жидкостью.

9.2. ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ ПО ТРУБАМ. ФОРМУЛА ПУАЗЕЙЛЯ

Течение вязкой жидкости по трубам представляет для медицины особый интерес, так как кровеносная система состоит в основном из цилиндрических сосудов разного диаметра.

Вследствие симметрии ясно, что в трубе частицы текущей жидкости, равноудаленные от оси, имеют одинаковую скорость. Наибольшей скоростью обладают частицы, движущиеся вдоль оси трубы; самый близкий к трубе слой жидкости неподвижен.

9.3. ДВИЖЕНИЕ ТЕЛ В ВЯЗКОЙ ЖИДКОСТИ. ЗАКОН СТОКСА

Вязкость проявляется при движении не только жидкости по сосудам, но и тел в жидкости. При небольших скоростях в соответствии с уравнением Ньютона сила сопротивления движущемуся телу пропорциональна вязкости жидкости, скорости движения тела и зависит от размеров тела. Так как невозможно указать общую формулу для силы сопротивления, ограничимся рассмотрением частного случая.

Наиболее простой формой тела является сфера. Для сферического тела (шарик) зависимость силы сопротивления при его движении в сосуде с жидкостью от перечисленных выше факторов выражается законом Стокса:

Формула (9.15) справедлива для движения шарика не только в жидкости, но и в газе. Она может быть использована, в частности, для вычисления времени выпадения пыли в воздухе. Поясним это следующим примером. Для воздуха - среды, в которой взвешены различные частицы пыли, - вязкость η = 0,000175 П ? с. Около 80% пыли, обнаруженной в легких умерших людей, составляют частицы размером от 5 до 0,2 мкм. Если считать пылинки шарообразными, а плотность пыли равной плотности земли (р = 2,5 г/см³), то, вычисляя скорость падения этих пылинок по формуле (9.15), найдем, что ее значения находятся в пределах 0,2-0,0003 см/с. Для полного выпадения такой пыли в комнате высотой 3 м потребуется около 12 суток при условии полной неподвижности воздуха и отсутствия броуновского движения.

9.4. МЕТОДЫ ОПРЕДЕЛЕНИЯ

ВЯЗКОСТИ ЖИДКОСТИ.

КЛИНИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ

ВЯЗКОСТИ КРОВИ

Совокупность методов измерения вязкости называют вискозиметрией, а приборы, используемые для таких целей, - вискозиметрами. Рассмотрим наиболее распространенные методы вискозиметрии.

Капиллярный метод основан на формуле Пуазейля и заключается в измерении времени протекания через капилляр жидкости известной

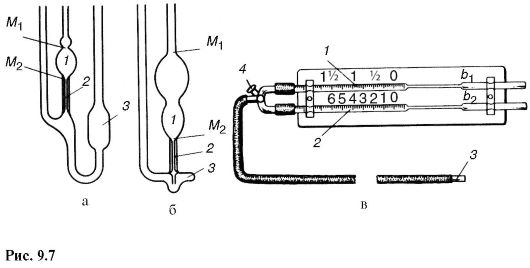
массы под действием силы тяжести при определенном перепаде давлений. Капиллярные вискозиметры различной формы показаны на рис. 9.7, а, б (1 - измерительные резервуары; М₁ и М₂ - метки, обозначающие границы этих резервуаров; 2 - капилляры; 3 - приемные сосуды).

Капиллярный вискозиметр применяется для определения вязкости крови.

Капиллярными вискозиметрами измеряют вязкость от значений 10^-5 Па ? с, свойственных газам, до значений 10⁴ Па ? с, характерных для консистентных смазок.

Метод падающего шарика используется в вискозиметрах, основанных на законе Стокса. Из формулы (9.15) находим

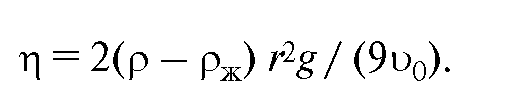
Таким образом, зная величины, входящие в правую часть этой формулы, и измеряя скорость равномерного падения шарика, можно найти вязкость данной жидкости.

Предел измерений вискозиметров с движущимся шариком составляет 6 ? 10⁴ - 250 Па ? с.

Применяются также ротационные вискозиметры, в которых жидкость находится в зазоре между двумя соосными телами, например цилиндрами. Один из цилиндров (ротор) вращается, а другой неподвижен. Вязкость измеряется по угловой скорости ротора, создающего определенный момент силы на неподвижном цилиндре, или по моменту силы,

действующему на неподвижный цилиндр, при заданной угловой скорости вращения ротора.

С помощью ротационных вискозиметров определяют вязкость жидкостей в интервале 1-10⁵ Пах, т.е. смазочных масел, расплавленных силикатов и металлов, высоковязких лаков и клеев, глинистых растворов и т.п.

В ротационных вискозиметрах можно менять градиент скорости, задавая разные угловые скорости вращения ротора. Это позволяет измерять вязкость при разных градиентах и установить зависимость η = /(άυ/άχ), которая характерна для неньютоновских жидкостей.

В настоящее время в клинике для определения вязкости крови используют вискозиметр Тесса с двумя капиллярами. Схема его устройства дана на рис. 9.7, в. Два одинаковых капилляра а₁Ь₁ и а₂Ь₂ соединены с двумя трубочками 1 и 2. Посредством резиновой груши или втягивая воздух ртом через наконечник 3, поочередно благодаря тройнику с краном 4 заполняют капилляр а₁Ь₁ и трубочку 1 до отметки 0 дистиллированной водой, а капилляр а₂Ь₂ и трубочку 2 до отметки 0 - исследуемой кровью. После этого теми же способами одновременно перемещают обе жидкости до тех пор, пока кровь не достигнет цифры 1, а вода - другой отметки в своей трубке. Так как условия протекания воды и крови одинаковы, то объемы наполнения трубок 1 и 2 будут различными вследствие того, что вязкости этих жидкостей неодинаковы. Хотя кровь и является неньютоновской жидкостью, используем с некоторым приближением формулу Пуазейля (9.8) и запишем очевидную пропорцию:

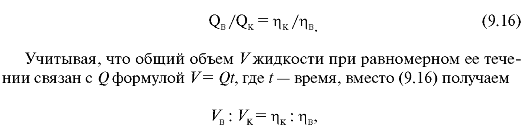
где V_K - объем крови в трубке 2 от отметки 0 до отметки 1; У_в - объем воды в трубке 1 от отметки 0 до отметки, полученной при измерении; η,, и соответственно вязкость крови и воды. Отношение вязкости крови и вязкости воды при той же температуре называют относительной вязкостью крови.

В вискозиметре Гесса объем крови всегда одинаков, а объем воды отсчитывают по делениям на трубке 1, поэтому непосредственно получают значение относительной вязкости крови. Для удобства отсчета сече-

ния трубок 1 и 2 делают различными, так, что, несмотря на разные объемы крови и воды, их уровни в трубках будут примерно одинаковы.

Вязкость крови человека в норме 4-5 мПа ? с, при патологии колеблется от 1,7-22,9 мПа ? с, что сказывается на скорости оседания эритроцитов (СОЭ). Венозная кровь обладает несколько большей вязкостью, чем артериальная. При тяжелой физической работе вязкость крови увеличивается. Некоторые инфекционные заболевания увеличивают вязкость, другие же, например брюшной тиф и туберкулез, - уменьшают.

9.5. ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ. ЧИСЛО РЕЙНОЛЬДСА

Рассмотренное ранее течение жидкости является слоистым, или ламинарным. Увеличение скорости течения вязкой жидкости вследствие неоднородности давления по поперечному сечению трубы создает завихрение и движение становится вихревым, или турбулентным. При турбулентном течении скорость частиц в каждом месте непрерывно и хаотически изменяется, движение является нестационарным.

Характер течения жидкости по трубе зависит от свойств жидкости, скорости ее течения, размеров трубы и определяется числом Рейнольдса:

Кинематическая вязкость полнее, чем динамическая, учитывает влияние внутреннего трения на характер течения жидкости или газа. Так, вязкость воды приблизительно в 100 раз больше, чем воздуха (при 0°С), но кинематическая вязкость воды в 10 раз меньше, чем воздуха, и поэтому вязкость сильнее влияет на характер течения воздуха, чем воды.

Как видно из (9.17), характер течения жидкости или газа существенно зависит от размеров трубы. В широких трубах даже при сравнительно небольших скоростях может возникнуть турбулентное движение. Так, например, в трубке диаметром 2 мм течение воды становится турбулентным при скорости более 127 см/с, а в трубе диаметром 2 см - уже при скорости примерно 12 см/с (температура 16 °С). Течение крови по такой трубе стало бы турбулентным при скорости 50 см/с, но практически в кровеносных сосудах диаметром 2 см турбулентное течение возникает даже при меньшей скорости.

Течение крови в артериях в норме является ламинарным, небольшая турбулентность возникает вблизи клапанов.

При патологии, когда вязкость бывает меньше нормы, число Рей-нольдса может превышать критическое значение и движение станет турбулентным.

Турбулентное течение связано с дополнительной затратой энергии при движении жидкости, что в случае крови приводит к добавочной работе сердца. Шум, возникающий при турбулентном течении крови, может быть использован для диагностирования заболеваний. Этот шум прослушивают на плечевой артерии при измерении давления крови.

Течение воздуха в носовой полости в норме ламинарное. Однако при воспалении или каких-либо других отклонениях от нормы оно может стать турбулентным, что повлечет дополнительную работу дыхательных мышц.

Число Рейнольдса является критерием подобия. При моделировании гидро- и аэродинамических систем, в частности кровеносной системы, модель должна иметь такое же число Рейнольдса, как и натура, в противном случае не будет соответствия между ними. Это относится и к моделированию обтекания тел при движении их в жидкости или газе.

Из (9.17) видно, что уменьшение размеров модели по сравнению с натурой должно быть скомпенсировано увеличением скорости течения или уменьшением кинематической вязкости модельной жидкости или газа.

9.6. ОСОБЕННОСТИ МОЛЕКУЛЯРНОГО СТРОЕНИЯ ЖИДКОСТЕЙ

Обычные жидкости изотропны, структурно они являются аморфными телами. Для внутреннего строения жидкостей характерен ближайший порядок (упорядоченное относительное расположение ближайших частиц). Расстояния между молекулами невелики, силы взаимодействия значительны, что приводит к малой сжимаемости жидкостей: небольшое уменьшение расстояния между молекулами вызывает появление больших сил межмолекулярного отталкивания. Подобно твердым телам, жидкости мало сжимаемы и обладают большой плотностью; подобно газам, принимают форму сосуда, в котором находятся. Такой характер свойств жидкостей связан с особенностями теплового движения их молекул. В газах молекулы движутся беспорядочно, на малых отрезках пути - поступательно, в расположении частиц отсутствует какой-либо порядок. В кристаллических телах частицы колеблются около определенных положений равновесия - узлов кристаллической решетки. По теории Я.И.Френкеля, молекулы жидкости, подобно частицам твердого тела, колеблются около положений равновесия, однако эти положения равновесия не являются постоянными. По истечении некоторого времени, называемого временем оседлой жизни, молекула скачком переходит в новое положение равновесия на расстояние, равное среднему расстоянию между соседними молекулами.

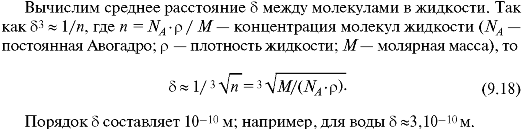
Среднее время оседлой жизни молекулы называют временем релаксации r. С повышением температуры и понижением давления время релаксации сильно уменьшается, что обусловливает большую подвижность молекул жидкости и малую ее вязкость.

Для того чтобы молекула жидкости перескочила из одного положения равновесия в другое, должны нарушиться связи с окружавшими ее молекулами и образоваться связи с новыми соседями. Процесс разрыва связей требует затраты энергии Е_а (энергия активации), выделяемой при образовании новых связей. Такой переход молекулы из одного положения равновесия в другое является переходом через потенциальный барьер

9.7. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ

На поверхностях раздела жидкости и ее насыщенного пара, двух не-смешиваемых жидкостей, жидкости и твердого тела возникает сила, обусловленная различным межмолекулярным взаимодействием граничащих сред.

Каждая молекула, расположенная внутри объема жидкости, равномерно окружена соседними молекулами и взаимодействует с ними, но равнодействующая этих сил равна нулю. На молекулу, находящуюся вблизи границы двух сред, вследствие неоднородности окружения действует сила, не скомпенсированная другими молекулами жидкости. Поэтому для перемещения молекул из объема в поверхностный слой необходимо совершить работу.

Поверхностное натяжение определяется отношением работы, затраченной на создание некоторой поверхности жидкости при постоянной температуре к площади этой поверхности:

Условием устойчивого равновесия жидкостей является минимум энергии поверхностного слоя, поэтому при отсутствии внешних сил или

в состоянии невесомости жидкость стремится иметь минимальную площадь поверхности при данном объеме и принимает форму шара.

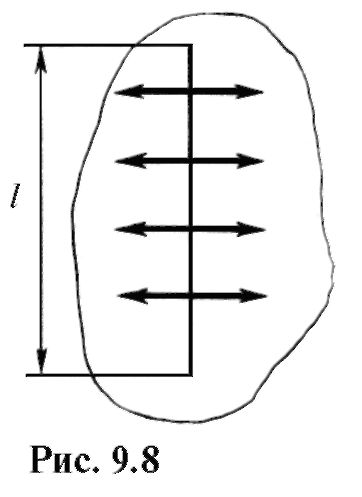
Поверхностное натяжение может быть определено не только энергетически. Стремление поверхностного слоя жидкости сократиться означает наличие в этом слое касательных сил - сил поверхностного натяжения. Если выбрать на поверхности жидкости некоторый отрезок длиной l (рис. 9.8), то можно условно изобразить эти силы стрелками, перпендикулярными отрезку.

Поверхностное натяжение равно отношению силы поверхностного натяжения к длине отрезка, на котором действует эта сила:

Из школьного курса физики известно, что оба определения, (9.21) и (9.22), тождественны. Приведем значения поверхностного натяжения для некоторых жидкостей при температуре 20 °С (табл. 1).

Таблица 1

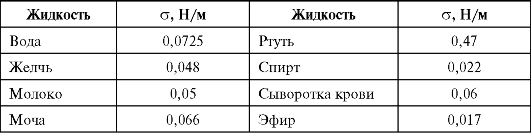
Поверхностное натяжение зависит от температуры. Вдали от критической температуры значение его убывает линейно при увеличении температуры. Снижения поверхностного натяжения можно достигнуть введением в жидкость поверхностно-активных веществ, уменьшающих энергию поверхностного слоя.

9.8. СМАЧИВАНИЕ И НЕСМАЧИВАНИЕ. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ

На границе соприкосновения различных сред может наблюдаться смачивание или несмачивание.

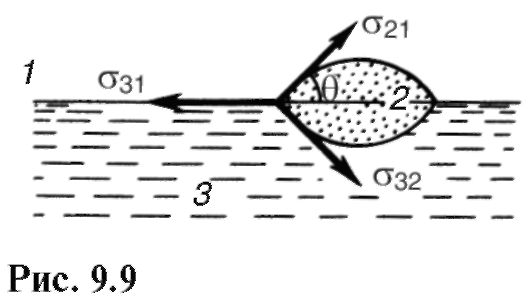
Рассмотрим поведение капли жидкости на поверхности другой, не смешивающейся с ней, жидкости (рис. 9.9) и капли жидкости на поверхности твердого тела (рис. 9.10 и 9.11). На поверхностях раздела каждых двух сред (1 и 3, 2 и 1, 3 и 2) действуют силы поверхностного натяжения.

Под действием сил поверхностного натяжения поверхностный слой жидкости искривлен и оказывает дополнительное по отношению к внешнему давление Др. Поверхностный слой подобен упругой оболочке, например резиновой пленке. Результирующая сил поверхностного натяжения искривленной поверхности направлена в сторону вогнуто-

ное количество жидкости из паров, что приводит к увлажнению белья, ваты в сырых помещениях, затрудняет сушку гигроскопических тел, способствует удержанию влаги в почве и т.п. Наоборот, несмачивающие жидкости не проникают в пористые тела. С этим связана, например, непроницаемость для воды перьев птиц, смазанных жиром.

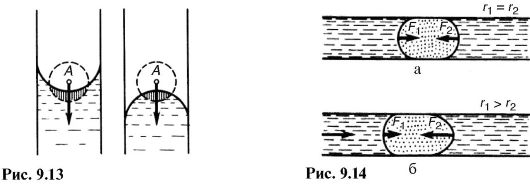
Рассмотрим поведение пузырька воздуха, находящегося в капилляре с жидкостью. Если давление жидкости на пузырек с разных сторон одинаково, то оба мениска пузырька будут иметь одинаковый радиус кривизны (рис. 9.14, а). При избыточном давлении с одной из сторон, например при движении жидкости, мениски деформируются, изменятся их радиусы кривизны (рис. 9.14, б), дополнительное давление Ар с разных сторон станет неодинаковым. Это приведет к такому воздействию на жидкость со стороны пузырька воздуха (газа), которое затруднит или прекратит движение жидкости. Такие явления могут происходить в кровеносной системе человека.

Попавшие в кровь пузырьки воздуха могут закупорить мелкий сосуд и лишить кровоснабжения какой-либо орган. Это явление, называемое эмболией, может привести к серьезному функциональному расстройству или даже летальному исходу. Так, воздушная эмболия может возникнуть при ранении крупных вен: проникший в ток крови воздух образует воздушный пузырь, препятствующий прохождению крови. Пузырьки воздуха не должны попадать в вены при внутривенных вливаниях.

Газовые пузырьки в крови могут появиться у водолазов при быстром подъеме с большой глубины на поверхность, у летчиков и космонавтов при разгерметизации кабины или скафандра на большой высоте (газовая эмболия). Это обусловлено переходом газов крови из растворенного состояния в свободное - газообразное в результате понижения окружающего атмосферного давления. Ведущая роль в образовании газовых пузырьков при уменьшении давления принадлежит азоту, так как он обусловливает основную часть общего давления газов в крови и не участвует в газообмене организма и окружающего воздуха.