Глава 7. Механические колебания и волны

Повторяющиеся движения или изменения состояния называют колебаниями (переменный электрический ток, движение маятника, работа сердца и т.п.). Всем колебаниям независимо от их природы присущи некоторые общие закономерности. Колебания распространяются в среде в виде волн. В данной главе рассматриваются механические колебания и волны.

7.1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Среди различных видов колебаний наиболее простой формой является гармоническое колебание, т.е. такое, при котором колеблющаяся величина изменяется в зависимости от времени по закону синуса или косинуса.

Пусть, например, материальная точка массой т подвешена на пружине (рис. 7.1, а). В этом положении упругая сила F₁ уравновешивает силу тяжести mg. Если оттянуть пружину на расстояние х(рис. 7.1, б), то на материальную точку будет действовать большая упругая сила. Изменение упругой силы, согласно закону Гука, пропорционально изменению длины пружины или смещению х точки:

F = -кх, (7.1)

где к - жесткость пружины; знак минус показывает, что сила всегда направлена в сторону положения равновесия: F < 0 при х > 0, F > 0 при х < 0.

Другой пример.

Математический маятник отклонен от положения равновесия на небольшой угол α (рис. 7.2). Тогда траекторию движения маятника можно считать прямой линией, совпадающей с осью ОХ. В этом случае выполняется приближенное равенство

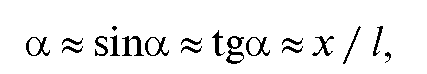
где х - смещение материальной точки относительно положения равновесия; l - длина нити маятника.

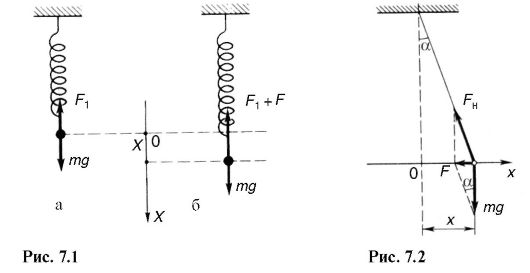
На материальную точку (см. рис. 7.2) действуют сила натяжения F_H нити и сила тяжести mg. Их равнодействующая равна:

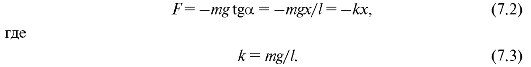
Сравнивая (7.2) и (7.1), видим, что в этом примере равнодействующая сила подобна упругой, так как пропорциональна смещению материальной точки и направлена к положению равновесия. Такие силы, неупругие по природе, но аналогичные по свойствам силам, возникающим при мальж деформациях упругих тел, называют квазиупругими.

Таким образом, материальная точка, подвешенная на пружине (пружинный маятник) или нити (математический маятник), совершает гармонические колебания.

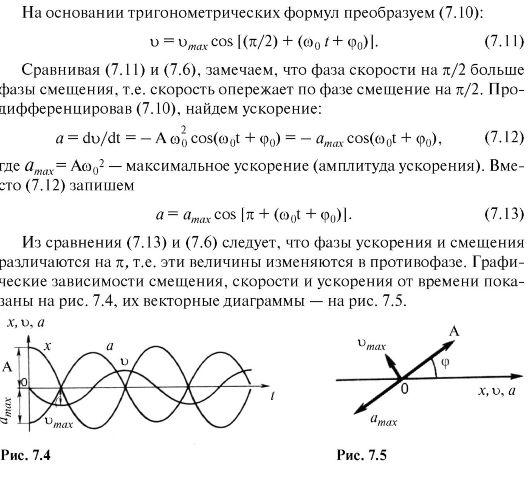
7.2. КИНЕТИЧЕСКАЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ

Кинетическую энергию колеблющейся материальной точки можно вычислить по известной формуле, используя выражение (7.10):

7.3. СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

Материальная точка может одновременно участвовать в нескольких колебаниях. В этом случае, чтобы найти уравнение и траекторию результирующего движения, следует сложить колебания. Наиболее просто выполняется сложение гармонических колебаний.

Рассмотрим две такие задачи.

Сложение гармонических колебаний, направленных по одной прямой.

Пусть материальная точка одновременно участвует в двух колебаниях, происходящих вдоль одной линии. Аналитически такие колебания выражаются следующими уравнениями:

т.е. амплитуда результирующего колебания равна сумме амплитуд слагаемых колебаний, если разность начальных фаз равна четному числу π (рис. 7.8, а);

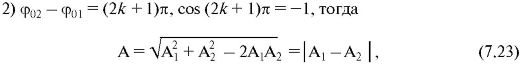
т.е. амплитуда результирующего колебания равна разности амплитуд слагаемых колебаний, если разность начальных фаз равна нечетному числу π (рис. 7.8, б). В частности, при А₁ = А₂ имеем А = 0, т.е. колебания нет (рис. 7.8, в).

Это достаточно очевидно: если материальная точка участвует одновременно в двух колебаниях, имеющих одинаковую амплитуду и совершающихся в противофазе, точка неподвижна. Если частоты складываемых колебаний не одинаковы, то сложное колебание уже не будет гармоническим.

Интересен случай, когда частоты слагаемых колебаний мало отличаются друг от друга: ω₀₁ и ω₀₂

Результирующее колебание при этом подобно гармоническому, но с медленно изменяющейся амплитудой (амплитудная модуляция). Такие колебания называются биениями (рис. 7.9).

Сложение взаимно перпендикулярных гармонических колебаний. Пусть материальная точка одновременно участвует в двух колебаниях: одно направлено вдоль оси ОХ, другое - вдоль оси OY. Колебания заданы следующими уравнениями:

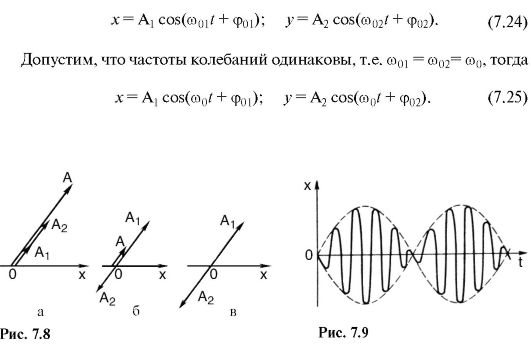
Уравнения (7.25) задают траекторию движения материальной точки в параметрической форме. Если в эти уравнения подставлять разные значения t, можно определить координаты х и у, а совокупность координат и есть траектория.

Таким образом, при одновременном участии в двух взаимно перпендикулярных гармонических колебаниях одинаковой частоты материальная точка движется по эллиптической траектории (рис. 7.10).

Из выражения (7.26) вытекают некоторые частные случаи:

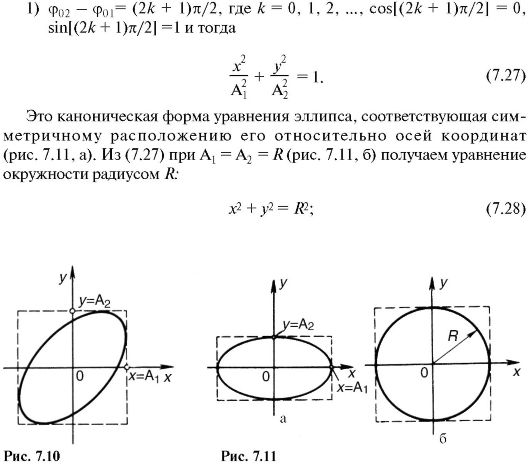
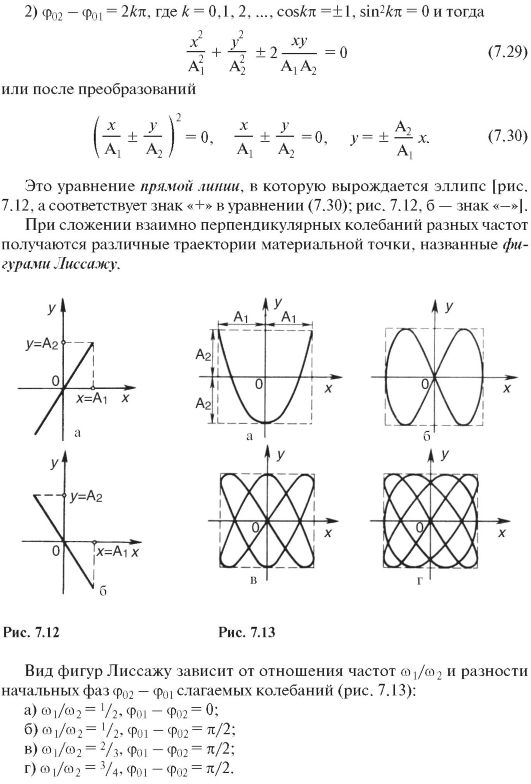
7.4. СЛОЖНОЕ КОЛЕБАНИЕ. ГАРМОНИЧЕСКИЙ СПЕКТР СЛОЖНОГО КОЛЕБАНИЯ

Как видно из 7.3, сложение колебаний приводит к более сложным формам колебаний. Для практических целей бывает необходимой противоположная операция: разложение сложного колебания на простые, обычно гармонические, колебания.

Фурье показал, что периодическая функция любой сложности может быть представлена в виде суммы гармонических функций, частоты которых кратны частоте сложной периодической функции. Такое разложение периодической функции на гармонические и, следовательно, разложение различных периодических процессов (механические, электрические и т.п.) на гармонические колебания называется гармоническим анализом. Существуют математические выражения, которые позволяют найти составляющие гармонические функции. Автоматически гармонический анализ колебаний, в том числе и для целей медицины, осуществляется специальными приборами - анализаторами.

Совокупность гармонических колебаний, на которые разложено сложное колебание, называется гармоническим спектром сложного колебания.

Гармонический спектр удобно представить как набор частот (или круговых частот) отдельных гармоник совместно с соответствующими им амплитудами. Наиболее наглядно такое представление выполняется графически. В качестве примера на рис. 7.14, а изображены графики сложного колебания (кривая 4) и составляющих его гармонических колебаний (кривые 1, 2и 3); на рис. 7.14, б показан гармонический спектр, соответствующий этому примеру.

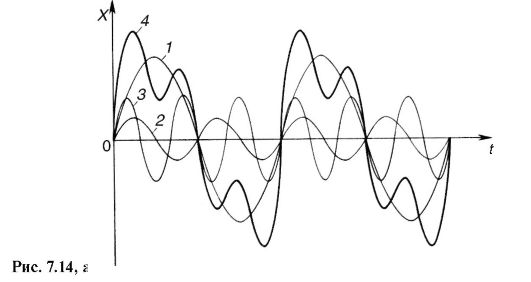
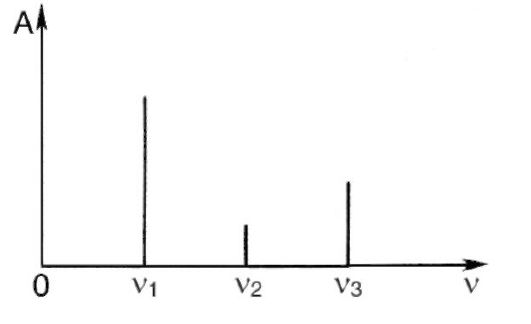
Рис. 7.14, б

Гармонический анализ позволяет достаточно детально описать и проанализировать любой сложный колебательный процесс. Он находит применение в акустике, радиотехнике, электронике и других областях науки и техники.

7.5. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

При изучении гармонических колебаний не учитывались силы трения и сопротивления, которые существуют в реальных системах. Действие этих сил существенно изменяет характер движения, колебание становится затухающим.

Если в системе кроме квазиупругой силы действуют силы сопротивления среды (силы трения), то второй закон Ньютона можно записать так:

Быстрота убывания амплитуды колебаний определяется коэффициентом затухания: чем больше β, тем сильнее тормозящее действие среды и тем быстрее уменьшается амплитуда. На практике, однако, степень затухания часто характеризуют логарифмическим декрементом затухания, понимая под этим величину, равную натуральному логарифму отношения двух последовательных амплитуд колебаний, разделенных интервалом времени, равным периоду колебаний:

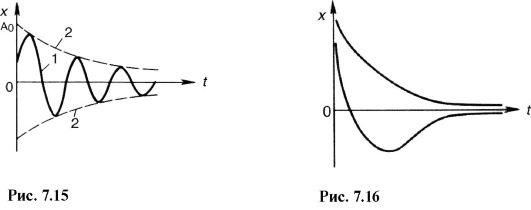
При сильном затухании (β² >>ω ²₀ ) из формулы (7.36) видно, что период колебания является мнимой величиной. Движение в этом случае уже называется апериодическим¹. Возможные апериодические движения представлены в виде графиков на рис. 7.16. Этот случай применительно к электрическим явлениям рассматривается более подробно в гл. 18.

Незатухающие (см. 7.1) и затухающие колебания называют соб-ственнъми или свободнъми. Они возникают вследствие начального смещения или начальной скорости и совершаются при отсутствии внешнего воздействия за счет первоначально накопленной энергии.

7.6. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС

Вынужденными колебаниями называются колебания, возникающие в системе при участии внешней силы, изменяющейся по периодическому закону.

Предположим, что на материальную точку, кроме квазиупругой силы и силы трения, действует внешняя вынуждающая сила:

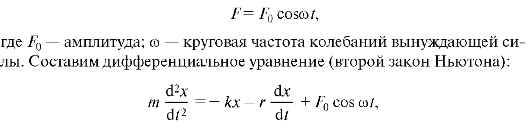
¹ Заметим, что если некоторая физическая величина принимает мнимые значения, то это означает какую-то необычность, экстраординарность соответствующего явления. В рассмотренном примере экстраординарность заключается в том, что процесс перестает быть периодическим.

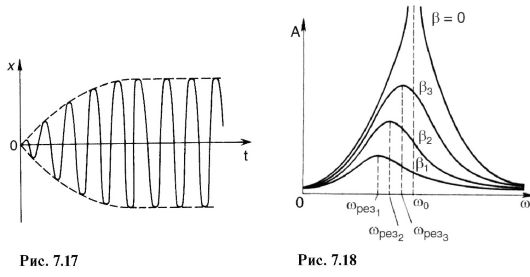
Из (7.43) видно, что при отсутствии сопротивления (β=0) амплитуда вынужденных колебаний при резонансе бесконечно большая. При этом из (7.42) следует, что ω_рез= ω₀ - резонанс в системе без затухания наступает тогда, когда частота вынуждающей силы совпадает с частотой собственных колебаний. Графическая зависимость амплитуды вынужденных колебаний от круговой частоты вынуждающей силы при разных значениях коэффициента затухания показана на рис. 7.18.

Механический резонанс может быть как полезным, так и вредным явлением. Вредное действие резонанса связано главным образом с разрушением, которое он может вызвать. Так, в технике, учитывая разные вибрации, необходимо предусматривать возможное возникновение резонансных условий, в противном случае могут быть разрушения и катастрофы. Тела обычно имеют несколько собственных частот колебаний и, соответственно, несколько резонансных частот.

Если коэффициент затухания внутренних органов человека был бы невелик, то резонансные явления, возникшие в этих органах под воздействием внешних вибраций или звуковых волн, могли бы привести к трагическим последствиям: разрыву органов, повреждению связок и т.п. Однако такие явления при умеренных внешних воздействиях практически не наблюдаются, так как коэффициент затухания биологических систем достаточно велик. Тем не менее резонансные явления при действии внешних механических колебаний происходят во внутренних органах. В этом, видимо, одна из причин отрицательного воздействия инфразвуковых колебаний и вибраций на организм человека (см. 8.7 и 8.8).

7.7. АВТОКОЛЕБАНИЯ

Как было показано в 7.6, колебания могут поддерживаться в системе даже при наличии сил сопротивления, если на систему периодически оказывается внешнее воздействие (вынужденные колебания). Это внешнее воздействие не зависит от самой колеблющейся системы, в то время как амплитуда и частота вынужденных колебаний зависят от этого внешнего воздействия.

Однако существуют и такие колебательные системы, которые сами регулируют периодическое восполнение растраченной энергии и поэтому могут колебаться длительное время.

Незатухающие колебания, существующие в какой-либо системе при отсутствии переменного внешнего воздействия, называются автоколебаниями, а сами системы - автоколебательными.

Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы, в отличие от вынужденных колебаний они не определяются внешними воздействиями.

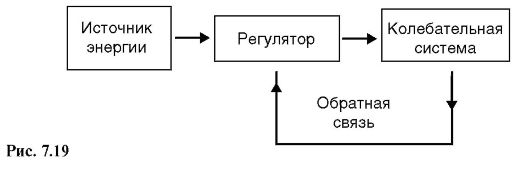
Во многих случаях автоколебательные системы можно представить тремя основными элементами:

1) собственно колебательная система;

2) источник энергии;

3) регулятор поступления энергии в собственно колебательную систему.

Колебательная система каналом обратной связи (рис. 7.19) воздействует на регулятор, информируя регулятор о состоянии этой системы.

Классическим примером механической автоколебательной системы являются часы, в которых маятник или баланс являются колебательной системой, пружина или поднятая гиря - источником энергии, а анкер - регулятором поступления энергии от источника в колебательную систему.

Многие биологические системы (сердце, легкие и др.) являются автоколебательными. Характерный пример электромагнитной автоколебательной системы - генераторы электромагнитных колебаний (см. гл. 23).

7.8. УРАВНЕНИЕ МЕХАНИЧЕСКИХ ВОЛН

Механической волной называют механические возмущения, распространяющиеся в пространстве и несущие энергию.

Различают два основных вида механических волн: упругие волны - распространение упругих деформаций - и волны на поверхности жидкости.

Упругие волны возникают благодаря связям, существующим между частицами среды: перемещение одной частицы от положения равновесия приводит к перемещению соседних частиц. Этот процесс распространяется в пространстве с конечной скоростью.

Уравнение волны выражает зависимость смещения s колеблющейся точки, участвующей в волновом процессе, от координаты ее равновесного положения и времени.

Для волны, распространяющейся вдоль некоторого направления ОХ, эта зависимость записывается в общем виде:

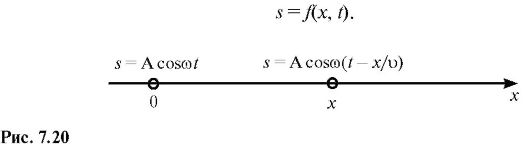
Если s и х направлены вдоль одной прямой, то волна продольная, если они взаимно перпендикулярны, то волна поперечная.

Выведем уравнение плоской волны. Пусть волна распространяется вдоль оси Х (рис. 7.20) без затухания так, что амплитуды колебаний всех точек одинаковы и равны А. Зададим колебание точки с координатой х = 0 (источник колебаний) уравнением

Решение уравнений с частными производными выходит за пределы данного курса. Одно из решений (7.45) известно. Однако важно отметить следующее. Если изменение какой-либо физической величины: механической, тепловой, электрической, магнитной и т.д., - отвечает уравнению (7.49), то это означает, что соответствующая физическая величина распространяется в виде волны со скоростью υ.

7.9. ПОТОК ЭНЕРГИИ ВОЛН. ВЕКТОР УМОВА

Волновой процесс связан с переносом энергии. Количественной характеристикой перенесенной энергии является поток энергии.

Поток энергии волн равен отношению энергии, переносимой волнами через некоторую поверхность, к времени, в течение которого эта энергия перенесена:

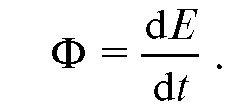
Единицей потока энергии волн является ватт (Вт). Найдем связь потока энергии волн с энергией колеблющихся точек и скоростью распространения волны.

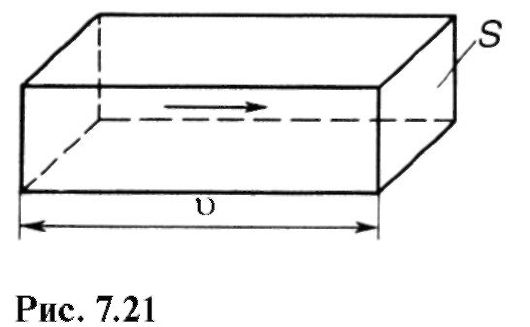
Выделим объем среды, в которой распространяется волна, в виде прямоугольного параллелепипеда (рис. 7.21), площадь поперечного сечения которого S, а длина ребра численно равна скорости υ и совпадает с направлением распространения волны. В соответствии с этим за 1 с сквозь площадку S пройдет та энергия, которой обладают колеблющиеся частицы в объеме параллелепипеда Sυ. Это и есть поток энергии волн:

7.10. УДАРНЫЕ ВОЛНЫ

Один из распространенных примеров механической волны - звуковая волна (см. гл. 8). В этом случае максимальная скорость колебаний отдельной молекулы воздуха составляет несколько сантиметров в секунду даже для достаточно большой интенсивности, т.е. она значительно меньше скорости волны (скорость звука в воздухе около 300 м/с). Это соответствует, как принято говорить, малым возмущениям среды.

Однако при больших возмущениях (взрыв, сверхзвуковое движение тел, мощный электрический разряд и т.п.) скорость колеблющихся частиц среды может уже стать сравнимой со скоростью звука, возникает ударная волна.

При взрыве высоконагретые продукты, обладающие большой плотностью, расширяются и сжимают слои окружающего воздуха. С течением времени объем сжатого воздуха возрастает. Поверхность, которая отделяет сжатый воздух от невозмущенного, в физике называют ударной волной. Схематично скачок плотности газа при распространении в нем ударной волны показан на рис. 7.22, а. Для сравнения на этом же рисунке показано изменение плотности среды при прохождении звуковой волны (рис. 7.22, б).

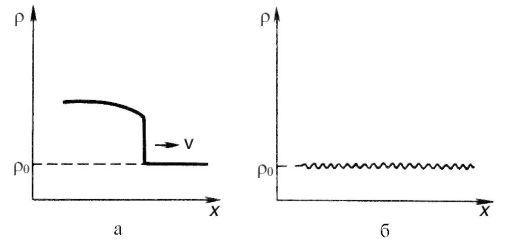
Рис. 7.22

Ударная волна может обладать значительной энергией, так при ядерном взрыве на образование ударной волны в окружающей среде затрачивается около 50% энергии взрыва. Поэтому ударная волна, достигая биологических и технических объектов, способна причинить смерть, увечья и разрушения.

7.11. ЭФФЕКТ ДОППЛЕРА

Эффектом Допплера называют изменение частоты волн, воспринимаемых наблюдателем (приемником волн), вследствие относительного движения источника волн и наблюдателя.