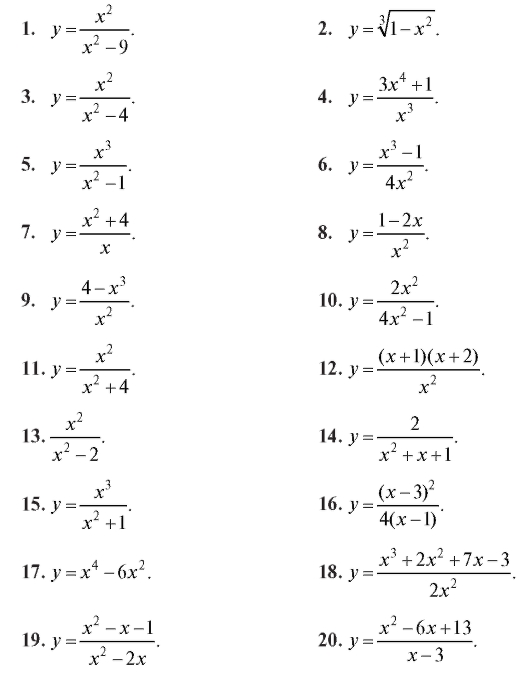Математика : учебник / И. В. Павлушков, Л. В. Розовский, И. А. Наркевич. - 2013. - 320 c. : ил.
|
|
|
|
Глава 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
2.1. ПРОИЗВОДНАЯ ФУНКЦИИ 2.1.1. Задачи, приводящие к понятию производной
Задача 1 (о скорости движущейся точки).
Пусть материальная точка движется по прямолинейной траектории, которую примем за ось Ох (рис. 2.1).
Положение точки на траектории будет тогда определяться ее
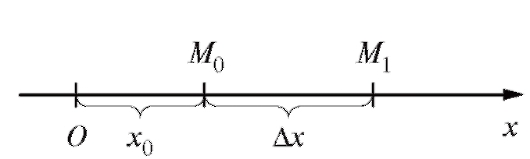
Рис. 2.1. Движение точки вдоль прямолинейной траектории
абсциссой x, которая является функцией времени t: x = f (t) (последнее равенство называется уравнением движения точки).
Пусть в момент времени t0 движущаяся точка занимала на траектории положение и имела абсциссу х0, а по прошествии времени
и имела абсциссу х0, а по прошествии времени переместилась в положение
переместилась в положение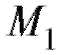 и имеет абсциссу
и имеет абсциссу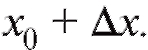 Таким образом, если за время
Таким образом, если за время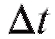 точка не меняла направление движения, то |Ax| - путь, пройденный точкой за время
точка не меняла направление движения, то |Ax| - путь, пройденный точкой за время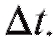 Очевидно, что
Очевидно, что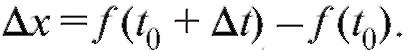
Назовем средней скоростью точки за время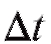 отношение
отношение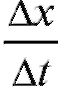 .
.
Определение. Мгновенной скоростью точки в момент времени to назовем предел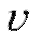 , к которому стремится средняя скорость точки за промежуток времени
, к которому стремится средняя скорость точки за промежуток времени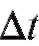 , когда
, когда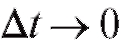 :
:
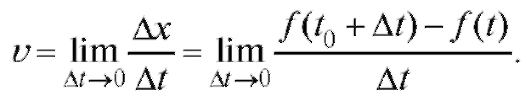 (2.1)
(2.1)
Пример. Точка свободно падает в пустоте. Вычислить скорость точки в произвольный момент t.
Решение. Уравнение свободного движения (падения) в этом случае имеет вид
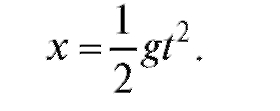
Тогда по формуле (2.1) находим:
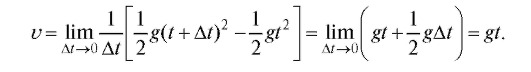
Задача 2 (о проведении касательной к плоскости кривой).
Пусть М0 - некоторая точка данной кривой (рис. 2.2).
Возьмем на этой кривой другую точку М и проведем секущую ММ0 . Пусть теперь точка М приближается вдоль кривой к точке М0 по любому закону так, что расстояние между этими точками стремится к нулю. Если при этом секущая ММ0 , поворачиваясь вокруг точки будет приближаться к некоторой прямой М0 Т так, что угол между прямыми и будет стремиться к нулю, то прямая называется касательной к данной кривой в точке
Заметим, что не всякая кривая обладает в каждой своей точке касательной. Прямая М0Т будет касательной к кривой в точке М0, если секущая ММ0 всегда стремится в указанном смысле к этой единственной прямой М0Т, по какому бы закону точка М ни стремилась по кривой к точке М0.
На рис. 2.3 представлена кривая, не имеющая касательной в точке М0. Здесь секущая ММ0 стремится к прямой М0N, если М → М0 слева. Если же М → М0 справа, то секущая ММ0 стремится к другой прямой - М0 L.
Пусть теперь в прямоугольной декартовой системе координат xOy задана кривая своим уравнением y = f (x). Требуется найти касательную к этой кривой в некоторой ее точке М0 с координатами (x0; y0) (рис. 2.4).
Легко написать искомое уравнение касательной, зная угловой коэффициент kо касательной к кривой в точке
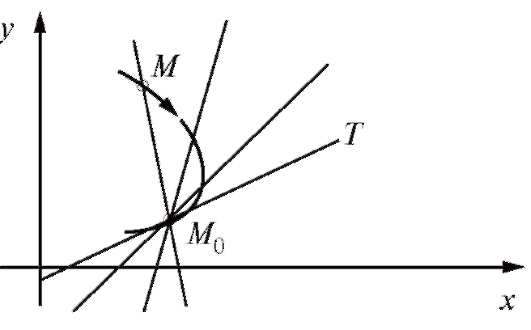
Рис. 2.2. Иллюстрация к определению касательной
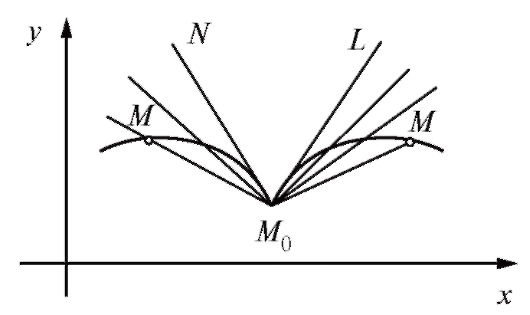
Рис. 2.3. Пример кривой, не имеющей касательной в точке Мо
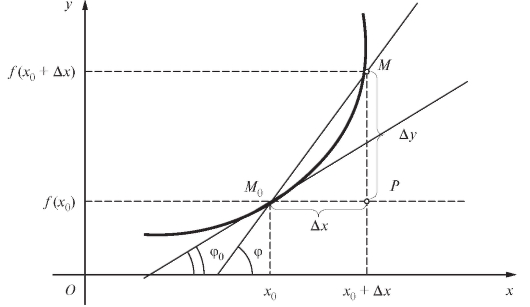
Рис. 2.4. Иллюстрация к задаче о проведении касательной к кривой y = f (x) в точке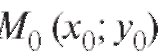
Возьмем на кривой другую точку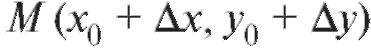 и проведем се-
и проведем се-
кущую Пусть
Пусть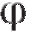 - угол наклона этой секущей к оси Ox. Наличие в точке касательной
- угол наклона этой секущей к оси Ox. Наличие в точке касательной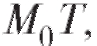 образующей с осью Ox угол
образующей с осью Ox угол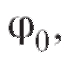 очевидно, эквивалентно равенству
очевидно, эквивалентно равенству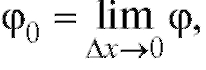 которое, в свою очередь, эквивалентно
которое, в свою очередь, эквивалентно
равенству
Но
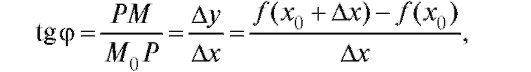
и, следовательно, формула (2.2) дает
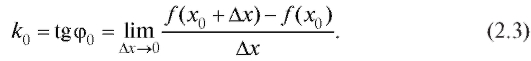
Значит, уравнение касательной примет вид
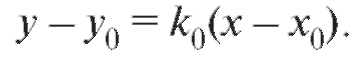
Пример. Вычислить угловой коэффициент касательной к кривой у = x3 в точке с абсциссой xo = 2. Написать уравнение касательной. Решение. По формуле (2.3) находим:
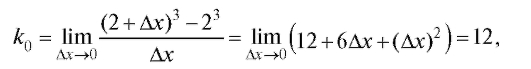
и, следовательно, уравнение касательной:
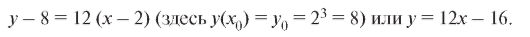
Заметим, что предел (2.3) имеет ту же структуру, что и предел (2.1). В обоих случаях отыскивается предел отношения приращения функции к приращению аргумента, вызвавшему это приращение, при условии, что приращение аргумента стремится к нулю.
2.1.2. Понятие производной
Пусть у = f (x) определена на некотором промежутке и xo- некоторая точка этого промежутка. Пусть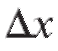 - приращение к значению аргумента, такое, что
- приращение к значению аргумента, такое, что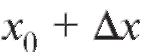 не выходит за пределы упомянутого промежутка, а
не выходит за пределы упомянутого промежутка, а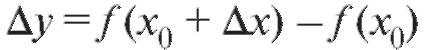 - соответствующее приращение функции.
- соответствующее приращение функции.
Определение. Если существует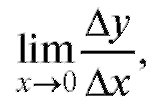 то этот предел называется
то этот предел называется
производной от функции y = f (x) по переменной x в точке хо (обозначения: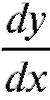 или
или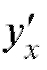 ). Итак:
). Итак:
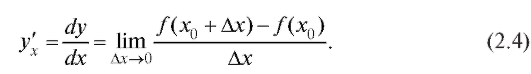
Если предел (2.4) конечен, то производная называется конечной, если же этот предел бесконечен, то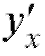 - бесконечная производная.
- бесконечная производная.
Если же конечная производная существует в каждой точке некоторого множества, то она оказывается функцией от x, заданной на этом множестве.
Пример. Найдем производную у = x2 на основании определения производной.
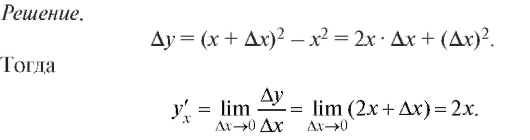
Геометрическая и механическая интерпретации производной
Используя результаты предыдущих пунктов, можно сформулировать следующие два предложения, содержащие механический и геометрический смысл производной.
1. Если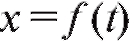 есть уравнение прямолинейного движения точки, то
есть уравнение прямолинейного движения точки, то
производная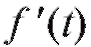 представляет собой скорость точки в момент времени t.
представляет собой скорость точки в момент времени t.
Быстрота протекания физических, химических, биологических и других процессов, например скорость охлаждения тела, скорость химической реакции и т. п., также выражается при помощи производной. Поясним это на примерах.
Пример 1. Предположим, что температура тела U есть убывающая функция времени: U = f (t). Пусть t - фиксированный момент времени. Если t получает приращение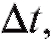 температура U уменьшается на
температура U уменьшается на тогда отношение
тогда отношение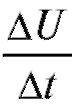 представляет собой среднюю скорость охлаждения
представляет собой среднюю скорость охлаждения
тела. Предел этого отношения при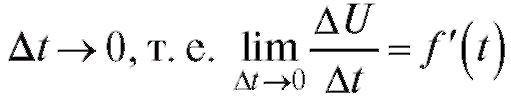 выражает
выражает
скорость охлаждения тела в данный момент t.
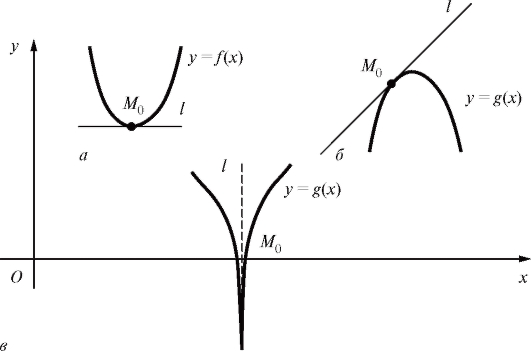
Рис. 2.5. Существование конечной и бесконечной производных: а, б - конечные производные в точке Мо (l - касательная; l не параллельна Oy); в - бесконечная производная в точке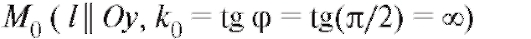
Таким образом, скорость охлаждения тела равна производной температуры тела по времени.
Пример 2. Обозначим через x количество вещества, образовавшегося при химической реакции за промежуток времени t.
Очевидно, x есть функция времени: x = f (t). Если t получает приращение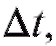 то x получает приращение
то x получает приращение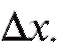 Тогда отношение представляет скорость химической реакции в данный момент t.
Тогда отношение представляет скорость химической реакции в данный момент t.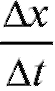
Таким образом, скорость химической реакции равна производной реагирующей массы по времени.
2. Производная f '(x) функции у = f (x) геометрически представляет собой угловой коэффициент касательной к графику этой функции в точке с абсциссой x.
При этом, если существует касательная, то существует и производная, и наоборот. Случаю касательной, не параллельной оси Oy, отвечает конечная производная, параллельная оси Oy - бесконечная производная (рис. 2.5).
Дифференцируемость функции в точке
Определение. Если приращение функции y = f (x) в точке x можно представить в форме:

где А не зависит от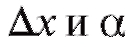 - бесконечно малая в точке x (см. п. 1.2.1), то
- бесконечно малая в точке x (см. п. 1.2.1), то
эта функция называется дифференцируемой в точке x. Из последнего равенства следует
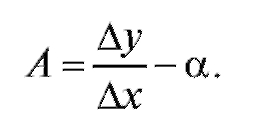
Перейдя здесь к пределу при получим
получим
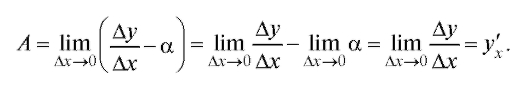
Итак, если y = f (x) дифференцируема в точке x, то приращение этой функции можно представить в виде

где а - бесконечно малая в точке x.
Отсюда следует, что если функция у = f (x) дифференцируема в точке x, то она обладает в этой точке конечной производной. Справедливо и обратное утверждение.
Другими словами, дифференцируемость функции в точке эквивалентна условию конечности производной f '(x) в этой точке.
Сформулируем связь дифференцируемости и непрерывности.
Теорема 2.1 (необходимое условие дифференцируемости).
Если функция y = f (x) дифференцируема в точке x, то она непрерывна в ней. Обратное утверждение, вообще говоря, неверно, т. е. из непрерывности не следует дифференцируемость. Для подтверждения сказанного рассмотрим две функции, графики которых представлены на рис. 2.6.
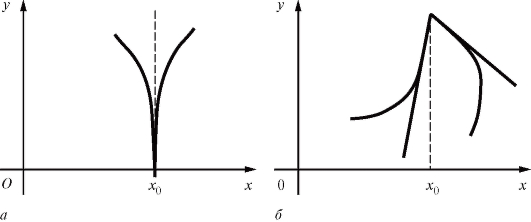
Рис. 2.6. Функции, не имеющие производной в точке хо
Обе эти функции непрерывны в точке но не будут дифференцируемы в этой точке. Касательная к графику на рис. 2.6, а в точке с абсциссой хо параллельна Oy, т. е. функция в этой точке имеет бесконечную производную. График второй функции (рис. 2.6, б) вообще не имеет и производной в точке хо.
2.1.3. Правила дифференцирования
1. Производная от постоянной величины равна нулю, т. е. если у = C, то у' = о:
2. Производная алгебраической суммы конечного числа функций равна сумме производных слагаемых:
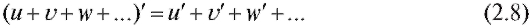
3. Производная произведения двух функций определяется формулой: 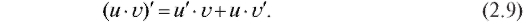 Аналогично,
Аналогично,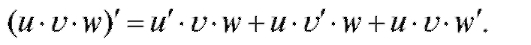
4. Производная частного от деления двух функций определяется формулой:

Дифференцирование сложной функции
Рассмотрим сложную функцию с одним промежуточным аргументом: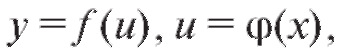 предполагая при этом, что функция у дифференцируема по аргументу u, а функция u дифференцируема по аргументу x. Требуется вывести правило дифференцирования этой сложной функции. Эвристические рассуждения, основанные на определении производной (см. также п. 1.2.2), приводят к соотношению
предполагая при этом, что функция у дифференцируема по аргументу u, а функция u дифференцируема по аргументу x. Требуется вывести правило дифференцирования этой сложной функции. Эвристические рассуждения, основанные на определении производной (см. также п. 1.2.2), приводят к соотношению
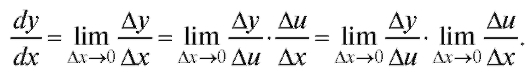
Если учесть, что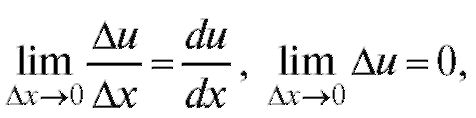 поскольку всякая диффе-
поскольку всякая диффе-
ренцируемая функция непрерывна, отсюда получим
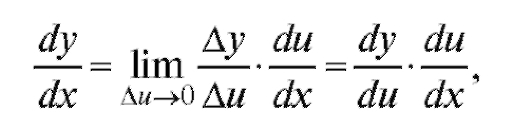
или в других обозначениях
Совершенно аналогично может быть выведено правило дифференцирования сложной функции с двумя промежуточными аргументами:
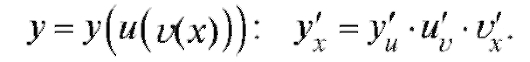
Пример 1. Из школьного курса математики известны производные функций:
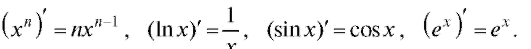
Найти у', если у = sin35x.
Решение. Производную этой сложной функции будем находить по формуле (2.11). Предположим, что данное у нужно вычислить при конкретном значении x (рис. 2.7).
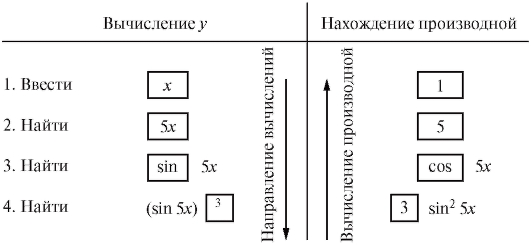
Рис. 2.7. Последовательность вычисления функции и ее производной
Таким образом, видно, что нахождение производной идет в порядке, обратном порядку вычисления функции.
Тогда по формуле (2.11) нам остается перемножить результаты, полученные на всех четырех ступенях, и
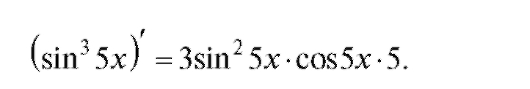
Пример 2. у = ln sine3x. Найти у'.
Решение. Действуя в соответствии со схемой, приведенной ранее, найдем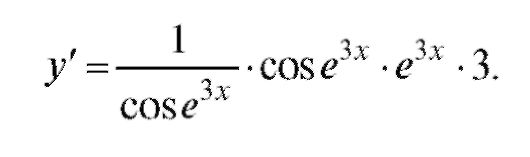
Рассмотрим производную обратной функции.
Предположим, что функция у = f (x) определена, монотонна и дифференцируема в некоторой области, причем производная dy/dx нигде не равна нулю. Наша функция у = f (x) имеет обратную функцию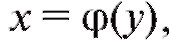 и нам надо получить правило дифференцирования этой функции. Для вывода можно воспользоваться правилом дифференцирования сложной функции с одним промежуточным аргументом. Согласно представлениям о сложной функции функцию у можно рассматривать как сложную функцию от самой себя с промежуточным аргументом x: у = f (x),
и нам надо получить правило дифференцирования этой функции. Для вывода можно воспользоваться правилом дифференцирования сложной функции с одним промежуточным аргументом. Согласно представлениям о сложной функции функцию у можно рассматривать как сложную функцию от самой себя с промежуточным аргументом x: у = f (x), 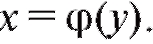
На основании правила дифференцирования сложной функции получаем: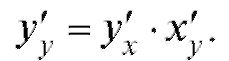
Поскольку у'у = 1, получаем правило дифференцирования обратной функции:
2.1.4. Производные от основных элементарных функций
1. Рассмотрим сначала производную от функции у = ln x:
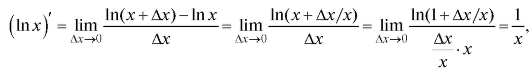
поскольку (см. п. 1.2.3)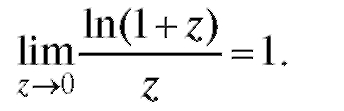 Итак,
Итак,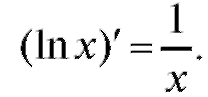
2. Получим формулу для производной логарифма с произвольным основанием. Формула перехода к другому основанию
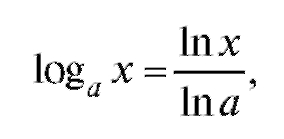
где ln a - постоянная. Следовательно,
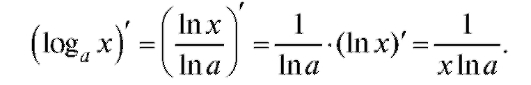
3. Рассмотрим производную от степенной функции у = хn. Сначала логарифмируем: ln у = п lnx. Дифференцируя и пользуясь
правилом дифференцирования сложной функции, получаем:
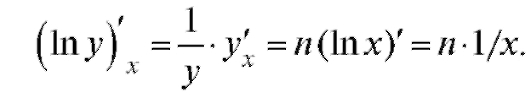
Окончательно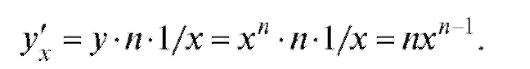 Итак,
Итак,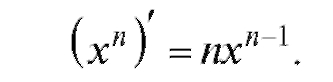
4. Рассмотрим производную от показательной функции у = ах. Совершенно аналогично предыдущему выводится формула
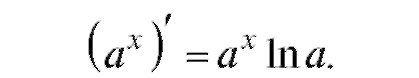
5. Рассмотрим производные от тригонометрических функций:
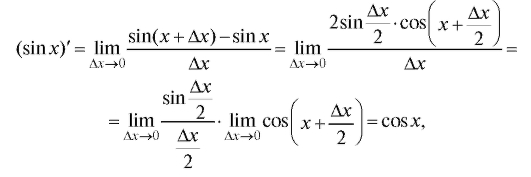
с учетом (1.19) и непрерывности функции cos x; 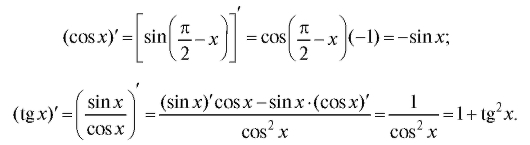 Итак,
Итак,
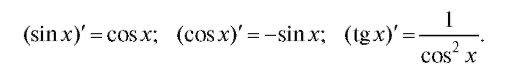
Совершенно аналогично выводится формула
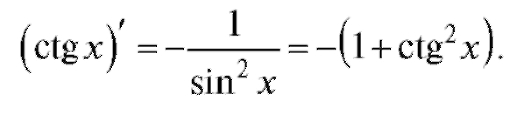
Перейдем к изложению вопроса о производных от обратных тригонометрических функций у = arcsin x, у = arccos x, у = arctg x, у = arcctg x.
Функции у = arcsin x соответствует обратная функция x = sin у при условии -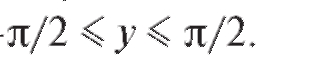
Согласно правилу дифференцирования обратной функции имеем 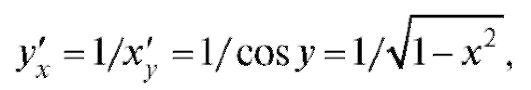
поскольку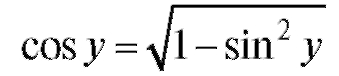 (здесь перед корнем выбран знак «+»,
(здесь перед корнем выбран знак «+»,
так как cos у > 0 для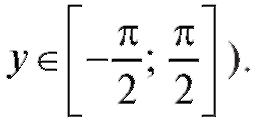 Итак,
Итак,
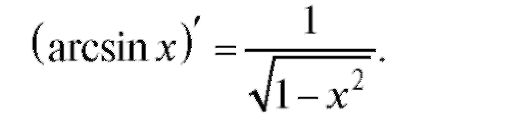
Совершенно аналогично получается формула
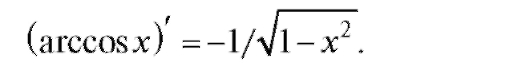
Функции у = arctg x соответствует обратная функция x = tg у при условии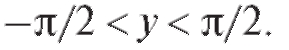
Согласно правилу дифференцирования обратной функции имеем 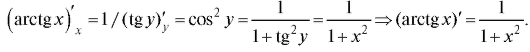 Аналогично:
Аналогично:
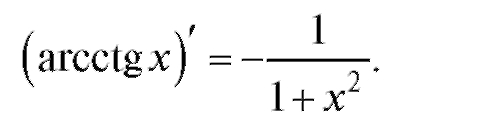
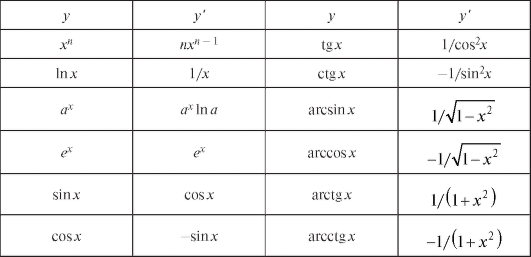
Составим сводную таблицу производных от основных элементарных функций (табл. 2.1).
Таблица 2.1. Производные основных элементарных функций
Полезно также помнить формулу для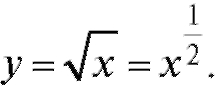 Тогда
Тогда
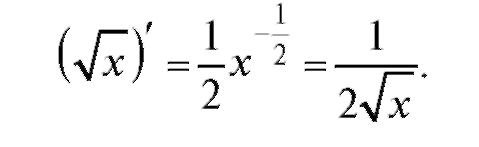
2.1.5. Логарифмическое дифференцирование
Дифференцирование многих функций значительно упрощается, если их предварительно прологарифмировать. Если функция y = f (x) есть произведение нескольких сомножителей, то можно сначала логарифмировать обе части уравнения y = f (x) (например, по основанию 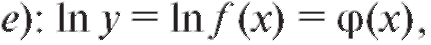 затем дифференцировать обе части полученного
затем дифференцировать обе части полученного
равенства: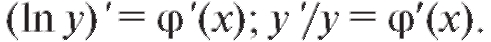
Отсюда, умножив обе части последнего уравнения на y = f (x), получим искомую производную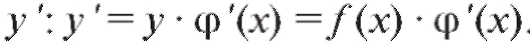
Логарифмическое дифференцирование полезно применять, когда заданная функция содержит логарифмирующиеся операции (умножение, деление, возведение в степень, извлечение корня) и, в частности, для дифференцирования показательно-степенной функции y = UV, где U и V - функции от x.
Пример. Найти производные от функций:
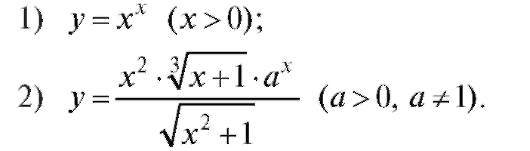
Решение.
1) y = xx. Сначала логарифмируем: ln y = x ln x. Теперь дифференцируем: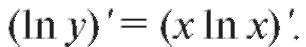 На основании формул и правил дифференцирования получаем y'/y = ln x + x • 1/x = ln x + 1. Отсюда y ' = y(ln x + 1) = xx(ln x + 1).
На основании формул и правил дифференцирования получаем y'/y = ln x + x • 1/x = ln x + 1. Отсюда y ' = y(ln x + 1) = xx(ln x + 1).
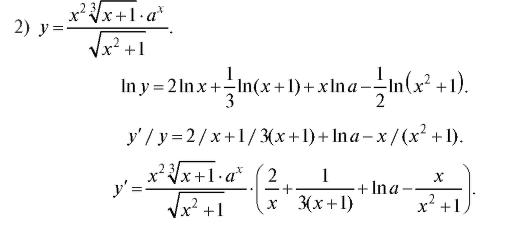
Самостоятельная работа
Найти производную функции (1-30).
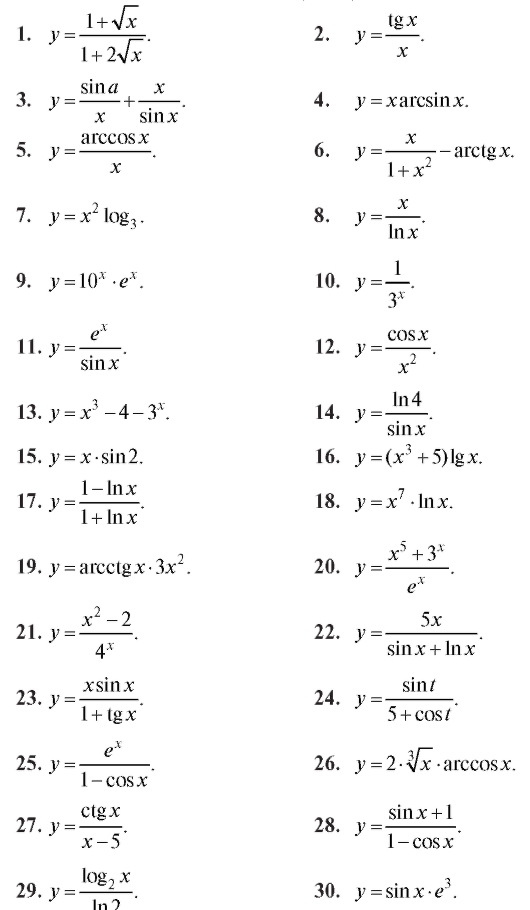
Найти производную сложной функции (31-60).

Используя логарифмическое дифференцирование, найти производную функции (61-70).

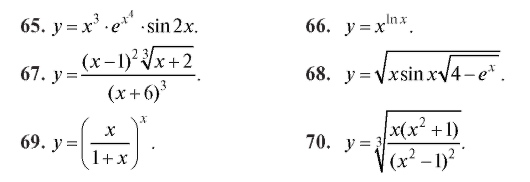
2.2. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 2.2.1. Определение
Согласно определению производной от функции y = f (x) имеем
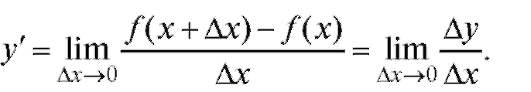
На основании определения предела (см. п. 1.2.1) это означает, что
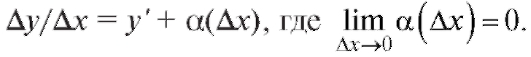 Отсюда
Отсюда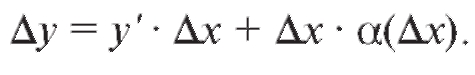
Первое слагаемое в правой части этого равенства стремится к нулю, как 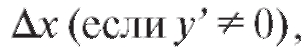 а второе слагаемое кроме
а второе слагаемое кроме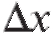 содержит в себе множитель
содержит в себе множитель 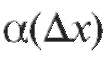 , который тоже стремится к нулю при
, который тоже стремится к нулю при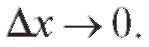 Таким образом, пер-
Таким образом, пер-
вое слагаемое стремится к нулю медленнее второго, и поэтому его называют главной частью приращения функции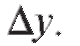
Определение. Главная часть приращения функции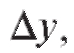 равная произведению
равная произведению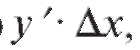 называется дифференциалом первого порядка от функции y = f (x), соответствующим выбранным значениям x и
называется дифференциалом первого порядка от функции y = f (x), соответствующим выбранным значениям x и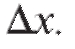 Обозначается так:
Обозначается так:

Это так называемая первая форма записи дифференциала.
Выясним геометрический смысл дифференциала.
На схематическом графике функции y = f (x) (рис. 2.8) отмечены две точки: точка А с абсциссой x и точка В с абсциссой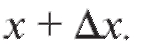 Производная
Производная
от функции y = f (x) в точке А равна угловому коэффициенту касательной к графику y = f (x) в этой точке. Поскольку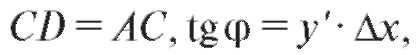 заключаем, что дифференциал dy равен приращению ординаты касательной к графику y = f (x), соответствующему значениям
заключаем, что дифференциал dy равен приращению ординаты касательной к графику y = f (x), соответствующему значениям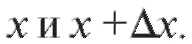
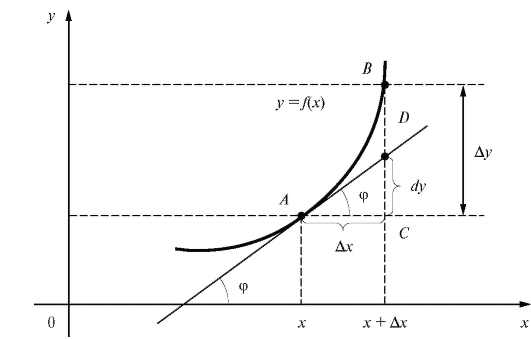
Рис. 2.8. Геометрический смысл дифференциала
Каков же механический смысл дифференциала? Если s = f (t) есть путь, пройденный материальной точкой за время t, то, как известно, производная ds/dt есть скорость движения в момент времени t. Тогда дифференциал пути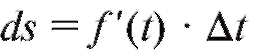 приближенно равен
приближенно равен
пути, пройденному материальной точкой от момента времени t до момента времени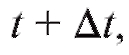 если пренебречь изменением скорости движения на этом промежутке времени.
если пренебречь изменением скорости движения на этом промежутке времени.
Кроме первой формы записи дифференциала существует и вторая. Дифференциалом аргумента называется дифференциал функции y = x, т. е.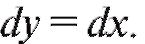 Однако на основании первой формы дифференциала имеем
Однако на основании первой формы дифференциала имеем
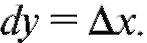 Следовательно,
Следовательно,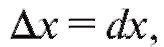 и мы получаем, таким образом, вторую
и мы получаем, таким образом, вторую
форму записи дифференциала

Вторая форма дифференциала обладает свойством инвариантности относительно аргумента, т. е. не зависит от того, является ли аргумент x окончательным или промежуточным. Поясним это на примере.
Пример. Требуется вычислить дифференциал функции y = (1 + tg x)8.
Решение. Это можно осуществить двумя способами.
1. Найдем y'(x) по правилам дифференцирования сложной функции:
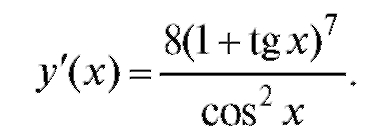
Тогда
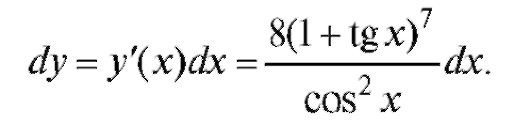
2. Введем новую функцию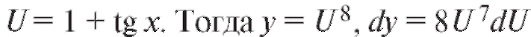 (как
(как
дифференциал функции y = y(u)). Вычислим dU:
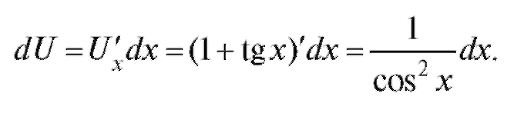
Следовательно,
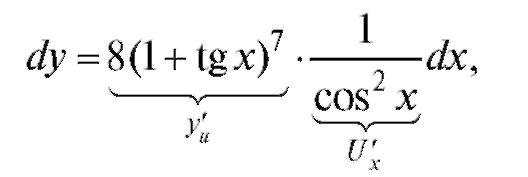
т. е. результат совпадает с результатом, вычисленным по первому способу.
Первая форма дифференциала таким свойством не обладает. Поскольку формально дифференциал отличается от производной лишь множителем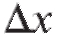 или dx, его свойства являются отражением соответствующих свойств производной.
или dx, его свойства являются отражением соответствующих свойств производной.
Например,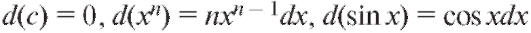 и т. д.
и т. д.
Пользуясь таблицей производных (см. табл. 2.1), мы можем написать таблицу дифференциалов от основных элементарных функций. Аналогично могут быть получены формулы:
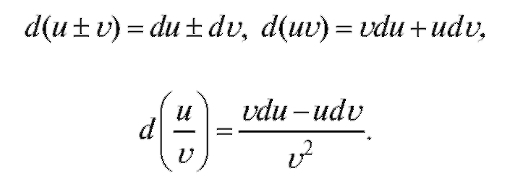
2.2.2. Приближенные вычисления с помощью дифференциала
Теорема 2.2. Если функция y = f (x) дифференцируема в точке x, причем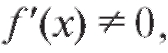 то приприращение
то приприращение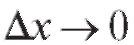 и
и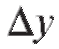 дифференциал dy функции являются эквивалентными бесконечно малыми.
дифференциал dy функции являются эквивалентными бесконечно малыми.
На этой теореме и основано применение дифференциала к приближенным вычислениям. Известно, что любую из двух эквивалентных бесконечно малых величин можно приближенно заменить другой. Следовательно:

Абсолютная и относительная погрешности этого равенства могут быть сделаны сколь угодно малыми при достаточно малом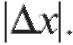 Структура дифференциала обычно значительно проще структуры приращения функции, в силу чего формула (2.15) широко применяется в приближенных вычислениях.
Структура дифференциала обычно значительно проще структуры приращения функции, в силу чего формула (2.15) широко применяется в приближенных вычислениях.
Пример 1. Дан куб с ребром x = 2 м. Вычислить, на сколько возрастет его объем, если ребро увеличится на 1 см.
Решение. Объем куба V = x3;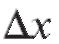 по условию задачи равно 0,01 м. Точное решение:
по условию задачи равно 0,01 м. Точное решение:
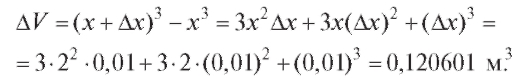
Таким образом, объем куба увеличится на 0,120601 м3. Приближенное решение:
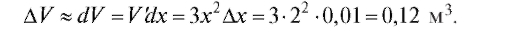
Абсолютная погрешность этого результата 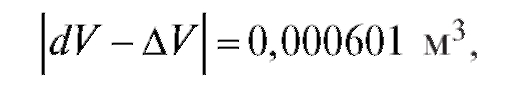 а относительная погрешность
а относительная погрешность
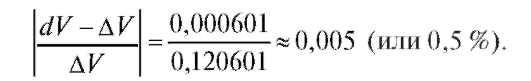
Пример 2. Вычислить приближенное значение ln 0,9.
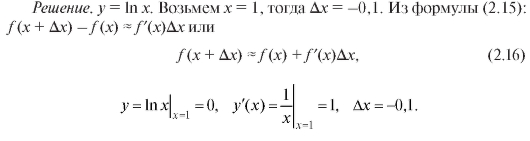
Эти результаты подставим в формулу (2.16). Тогда
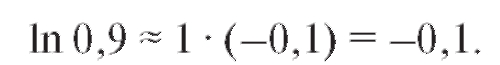
Пример 3. Приближенно вычислить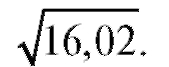 Решение. Пусть в формуле (2.15)
Решение. Пусть в формуле (2.15)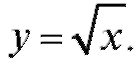 Тогда
Тогда
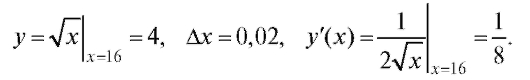
Следовательно,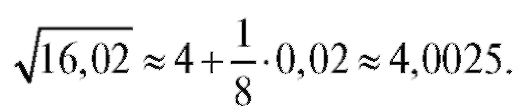
2.2.3. Производные и дифференциалы высших порядков
Пусть функция y = f (x) дифференцируема на некотором промежутке. Тогда производная f '(x) этой функции будет новой функцией от x, заданной на этом промежутке, и может в свою очередь иметь производную. Эту производную называют производной второго порядка и обозначают одним из символов:
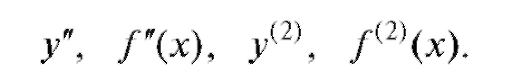
Производную от второй производной называют третьей производной и т. д. Вообще,
Пример.
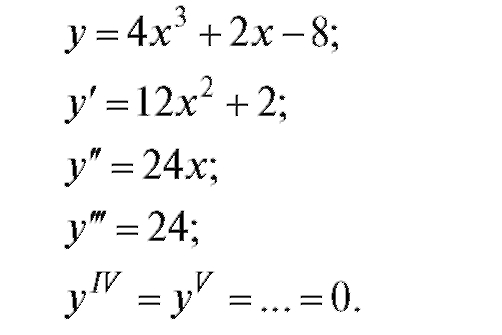
Отметим, что для многочлена степени n все производные, начиная с (n + 1)-го порядка, равны нулю.
Теперь рассмотрим дифференциалы высшего порядка.
Дифференциал функции y = f (x), где x - независимая переменная, определяется формулой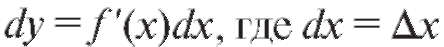 - произвольное прира-
- произвольное прира-
щение аргумента x. Зафиксируем dx; тогда dy будет функцией от x. Дифференциал от этой функции называют дифференциалом второго порядка и обозначают d2y или d2f (x).
Поскольку dx зафиксирован (постоянен), то
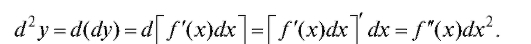
Аналогично определяются дифференциалы для любого n > 2:

Итак, дифференциал n-го порядка функции равен произведению n-й производной этой функции на n-ю степень дифференциала независимой переменной.
Если имеется сложная функция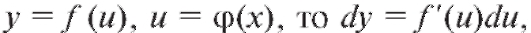 но теперь уже
но теперь уже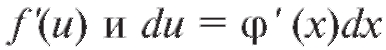 являются функциями от x. Поэтому
являются функциями от x. Поэтому
при отыскании повторных дифференциалов здесь нельзя выносить du за знак производной, а надо дифференцировать произведение. Формулы для дифференциалов высших порядков сложной функции отличаются от последней формулы, и дифференциалы второго и высших порядков свойством инвариантности по отношению к аргументу уже не обладают.
Самостоятельная работа
1. Найти приращение функции y = x2, соответствующее приращению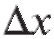 независимой переменной. Вычислить
независимой переменной. Вычислить если x = 1 и
если x = 1 и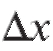 = 0,1.
= 0,1.
2. Найти приращение объема V шара при изменении радиуса R = 2 на
объема V шара при изменении радиуса R = 2 на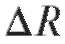 = 0,1. Вычислить
= 0,1. Вычислить
3. Дана функция y = x3 + 2x. Найти значения приращения и его линейной главной части, соответствующие изменению x от x = 2 до x = 2,1.
4. Найти приращение и дифференциал функции y = x2 - x при x = 10 и = 0,1. Вычислить абсолютную и относительную ошибки, которые получаются при замене приращения дифференциалом.
= 0,1. Вычислить абсолютную и относительную ошибки, которые получаются при замене приращения дифференциалом.
5. Вычислить приближенно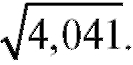
6. Сторона квадрата равна 8 см. На сколько увеличится его площадь, если каждую его сторону увеличить на 0,1 см?
7. Вычислить значение дифференциала функции:
1) 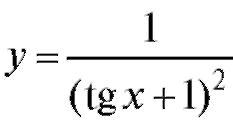 при изменении
при изменении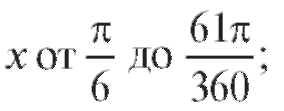
2)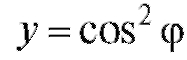 при изменении
при изменении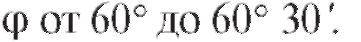
8. Дана функция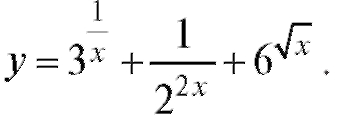 Вычислить dy при x = 1 и dx = 0,2.
Вычислить dy при x = 1 и dx = 0,2.
Вычислить приближенно (9-13).
9. sin 60° 18.
10. arctg 1,02.
11.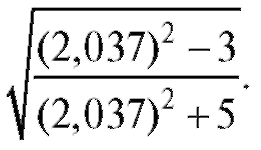
12. arcsin 0,4983. 13.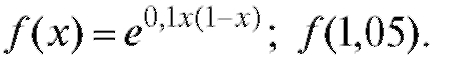
Повторное дифференцирование.
Вычислить производную функции (14-23).
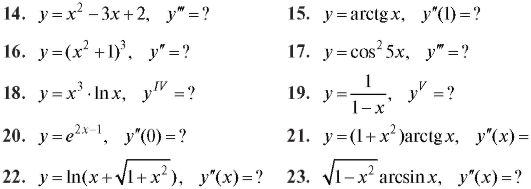
2.3. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ 2.3.1. Касательная и нормаль к плоской кривой
Если плоская кривая, являющаяся графиком функции y = f (x) в декартовой системе координат, имеет в точке M0 с координатами (x0; f (x0)) касательную и нормаль, ни одна из которых не параллельна оси Oy, то их уравнения имеют вид
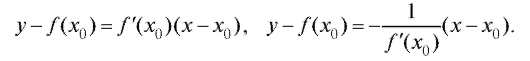
Направление кривой в каждой точке определяется направлением касательной к ней в этой точке.
Пример. Составить уравнения касательной и нормали: 1)к параболе y = x2 - 3x, где x = 1;
2) к окружности x2 + y2 - 2x + 4y - 3 = 0 в точках пересечения ее с
осью Ox. Решение.
1) y = x2 - 3x. Если x = 1, то y = 1 - 3 = -2, y' = 2x - 3. В точке x = 1 y' = 2x - 3.
Уравнение касательной: y + 2 = -1 • (x - 1), или x + y + 1 = 0. Уравнение нормали: y + 2 = x - 1, или y - x + 3 = 0.
2) x2 + y2 - 2x + 4y - 3 = 0. В точках пересечения с осью Ох y = 0. Значит, x2 - 2x - 3 = 0; x1 = -1; x2 = 3. Найдем угловые коэффициенты касательных.
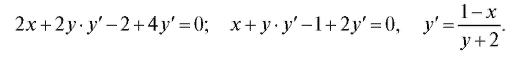
В точке (-1; 0)
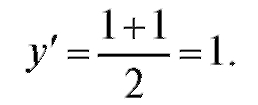
Уравнение касательной: y = (x + 1), или x - y + 1 = 0. Уравнение нормали: y = -(x + 1), или x + y + 1 = 0. В точке (3; 0)
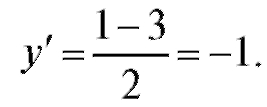
Уравнение касательной: y = -(x - 3), или x + y - 3 = 0. Уравнение нормали: y = (x - 3), или x - y - 3 = 0.
2.3.2. Скорость изменения переменной величины
Скорость и ускорение прямолинейного движения
Если z есть функция времени t, то скорость ее изменения определяется производной dz/dt.
Если точка движется прямолинейно, то ее скорость υ и ускорение w определяются первой и второй производными от пути s по времени t:
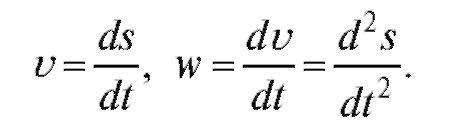
Поясним эти положения примерами.
Пример 1. Зависимость количества Q вещества, получаемого в химической реакции, от времени t определяется формулой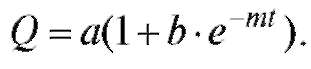 Определить скорость реакции.
Определить скорость реакции.
Решение. Скорость реакции есть производная
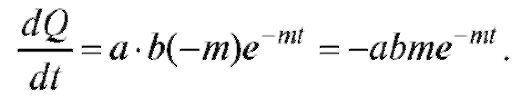
Пример 2. Скорость прямолинейного движения тела пропорциональна корню квадратному из пройденного пути. Доказать, что движение происходит под действием постоянной силы.
Решение. По закону Ньютона сила F, вызывающая движение, пропорциональна ускорению:
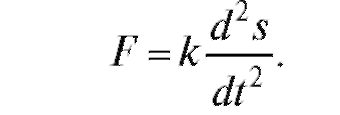
Согласно условию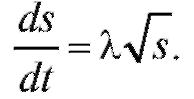 Отсюда
Отсюда
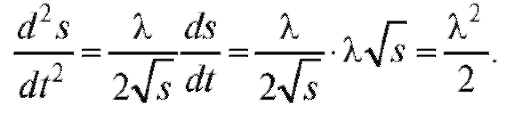
Это значит, что действующая сила F постоянная и равна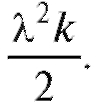
Самостоятельная работа
1. Найти уравнения касательных и нормалей к гиперболе y2 - 2x2 = 1 в точках, где x = 2.
Рассмотрим теперь еще два важных приложения производной:
• правило Лопиталя (вычисление пределов с помощью производных);
• исследование функций с помощью производных и построение графиков функций.
2.3.3. Правило Лопиталя
Пусть требуется вычислить предел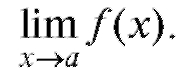 Если f (x) - элементар-
Если f (x) - элементар-
ная функция и а принадлежит области ее определения, то для вычисления этого предела нужно перейти к пределу под знаком функции f (x), что приводит к подстановке в f (x) вместо x предельного значения а:
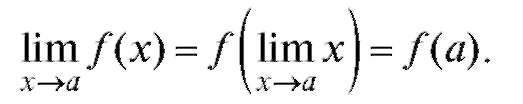
Если же а не принадлежит области определения функции f (x), то формальное применение правил предельного перехода приводит к одному из следующих символов:
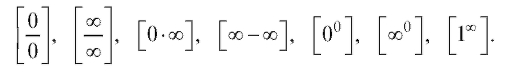
Напоминаем (см. п. 1.2.3), что в этом случае в точке а имеет место неопределенность соответствующего типа, а вычисление предела в этом случае называют раскрытием неопределенности.
Теорема 2.3. Если функции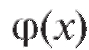 и g(x) дифференцируемы в некоторой окрестности точки а и при x → a одновременно стремятся к нулю или бесконечности, причем
и g(x) дифференцируемы в некоторой окрестности точки а и при x → a одновременно стремятся к нулю или бесконечности, причем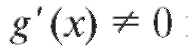 в данной окрестности (исключая,
в данной окрестности (исключая,
может быть, саму точку а), то
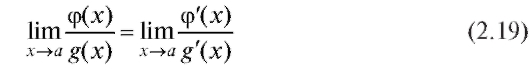
при условии, что предел в правой части (2.19) существует. (Заметим, что а здесь может быть числом или одним из символов: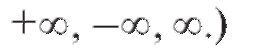
Из данной теоремы вытекает следующее практическое правило раскрытия неопределенностей первых двух типов, называемое правилом
Лопиталя: для раскрытия неопределенностей вида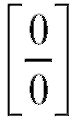 или
или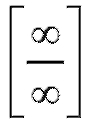 нужно
нужно
от предела отношения двух функций перейти к пределу отношения производных. Если отношение производных стремится к некоторому пределу (конечному или бесконечному), то к этому же пределу стремится и отношение функции.
Пример 1.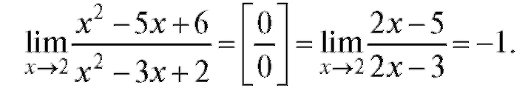 Пример 2.
Пример 2.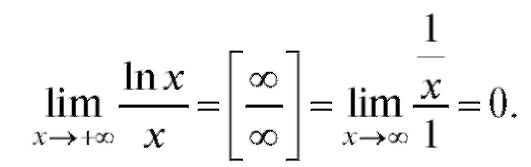
Может случиться так, что отношение производных снова приведет к неопределенности вида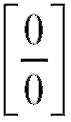 или
или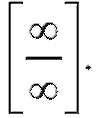 Тогда, рассматривая производ-
Тогда, рассматривая производ-
ные как исходные функции, перейдем к пределу отношения вторых производных и т. д.:
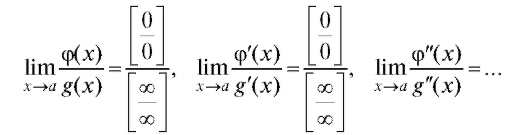
Если на некотором шаге мы получим предел, то его значение и будет искомым пределом отношения исходных функций.
Пример 3.
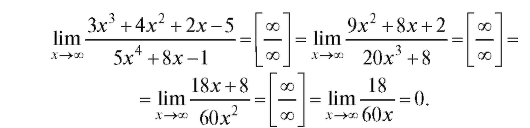
Пример 4.
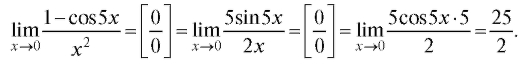
При применении формулы (2.19) может оказаться, что предел в правой ее части не существует. Это говорит лишь о том, что правило Лопиталя не применимо, и нужно вычислять исходный предел каким-либо другим способом.
Пример 5.
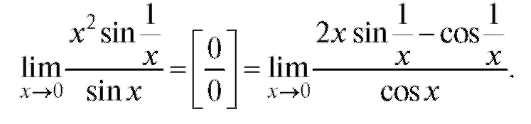
Этот последний предел не существует, так как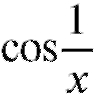 при
при преде-
преде-
ла не имеет, поэтому правило Лопиталя не применимо. Вычислим предел иным способом:
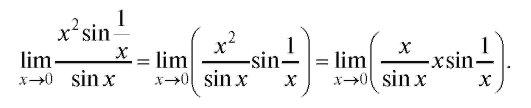
Так как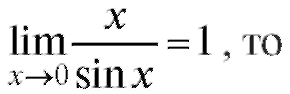
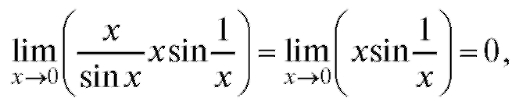
так как x - бесконечно малая при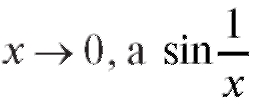 ограничена.
ограничена.
К неопределенности видаможно легко свести и другие
виды неопределенностей: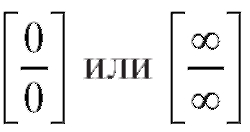
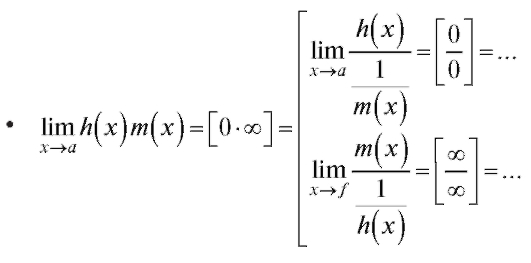
т. е. неопределенность вида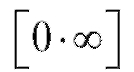 можно привести к одной из
можно привести к одной из
стандартных неопределенностей для дальнейшего применения правила Лопиталя;
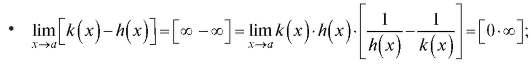
неопределенности видов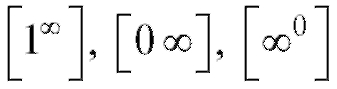 раскрываются с по-
раскрываются с по-
мощью основного логарифмического тождества:
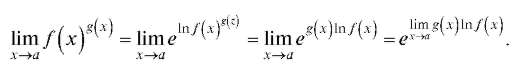
Для всех трех рассматриваемых случаев вычисление предела 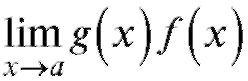 снова приведет к раскрытию неопределенности вида
снова приведет к раскрытию неопределенности вида
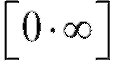 , о которой мы говорили в первом пункте.
, о которой мы говорили в первом пункте.
Пример 6. Найти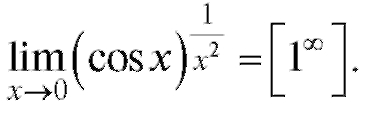 Решение.
Решение.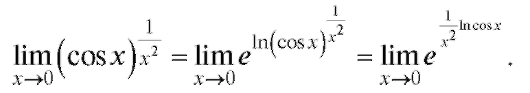
Вычисление последнего предела сводится к вычислению предела от его показателя:
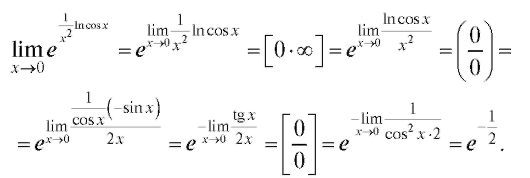
Правило Лопиталя часто используется при отыскании асимптот плоских кривых.
Самостоятельная работа
Используя правило Лопиталя, вычислить (1-30).
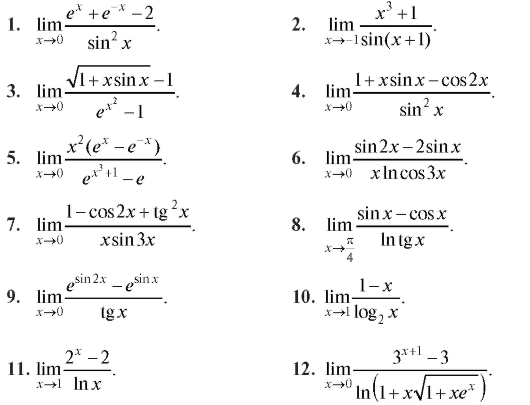

2.3.4. Отыскание асимптот плоских кривых
Пусть кривая является графиком функции y = f (x). Пусть при
 эта кривая неограниченно приближается к некоторой прямой y = kx + b. В этом случае данная прямая называется асимптотой кривой, причем при
эта кривая неограниченно приближается к некоторой прямой y = kx + b. В этом случае данная прямая называется асимптотой кривой, причем при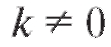 - наклонной асимптотой (рис. 2.9), а при k = 0 - горизонтальной.
- наклонной асимптотой (рис. 2.9), а при k = 0 - горизонтальной.
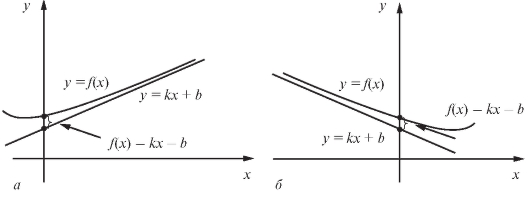
Рис. 2.9. Наклонные асимптоты кривой:
Определение. Прямая y = kx + b называется асимптотой кривой y = f (x) при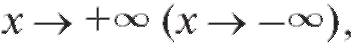 если
если
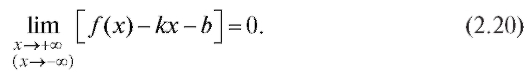
Пусть кривая y = f (x) имеет асимптоту y = kx + b при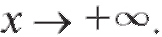 Тогда,
Тогда,
согласно определению, имеет место равенство (2.20). Разделим (2.20) на x:
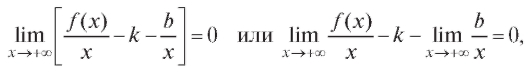
откуда
из определения также следует, что
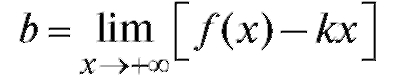
Таким образом, если кривая имеет асимптоту y = kx + b при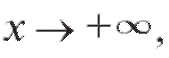 то справедливы равенства (2.20), (2.21), и, наоборот, если выполняются равенства (2.20) и (2.21), то кривая имеет асимптоту y = kx + b.
то справедливы равенства (2.20), (2.21), и, наоборот, если выполняются равенства (2.20) и (2.21), то кривая имеет асимптоту y = kx + b.
Те же самые рассуждения справедливы при Заметим, что если, по крайней мере, один из пределов (2.20), (2.21) не существует или бесконечен, то кривая не имеет асимптоты при
Заметим, что если, по крайней мере, один из пределов (2.20), (2.21) не существует или бесконечен, то кривая не имеет асимптоты при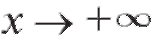
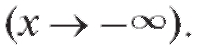
Пример 1. Для функции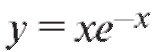 найти асимптоту.
найти асимптоту.
Решение. Находим асимптоту при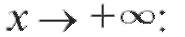
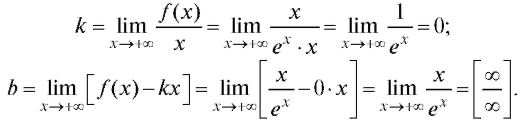
Воспользуемся правилом Лопиталя и получим
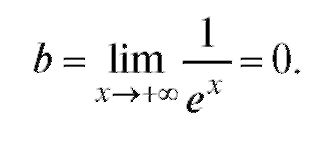
Следовательно, данная функция имеет горизонтальную (так как k = 0) асимптоту y = 0. Найдем асимптоту при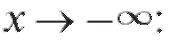
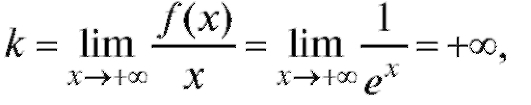
т. е. при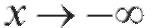 асимптоты график не имеет.
асимптоты график не имеет.
Пример 2. Для функции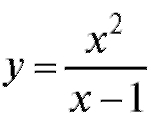 найти асимптоту.
найти асимптоту.
Решение. Здесь
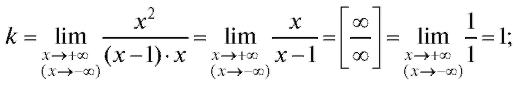
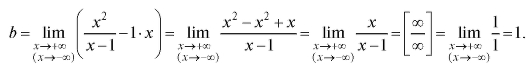
Итак, k = 1, b = 1. Следовательно, график имеет асимптоту y = x + 1, причем как в случае так и в случае
так и в случае
Пусть a - некоторое число. Если кривая y = f (x) неограниченно приближается к вертикальной прямой x = a при то эта прямая, параллельная оси Oy, называется вертикальной асимптотой (рис. 2.10).
то эта прямая, параллельная оси Oy, называется вертикальной асимптотой (рис. 2.10).
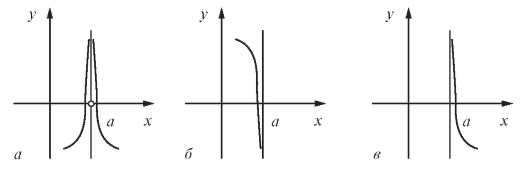
Рис. 2.10. Вертикальные асимптоты кривой: а - при ; б - при
; б - при
в -
Итак, прямая x = a называется вертикальной асимптотой кривой y = f (x), если выполняется одно из трех условий:
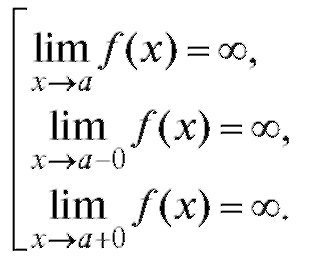
Следовательно, для отыскания вертикальных асимптот нужно найти точки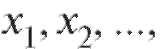 вблизи которых f (x) неограниченно возрастает по модулю.
вблизи которых f (x) неограниченно возрастает по модулю.
Тогда прямые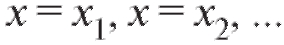 будут
будут
являться вертикальными асимптотами.
Пример 3. Для функции 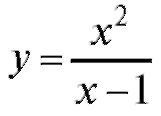 найти асимптоту.
найти асимптоту.
Решение. Точка x = 1 не входит в область определения данной функции. Вычислим пределы:
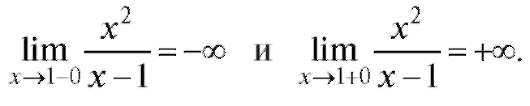
Следовательно, x = 1 - уравнение вертикальной асимптоты, причем вблизи точки x = 1 функция будет вести себя так, как показано на рис. 2.11.
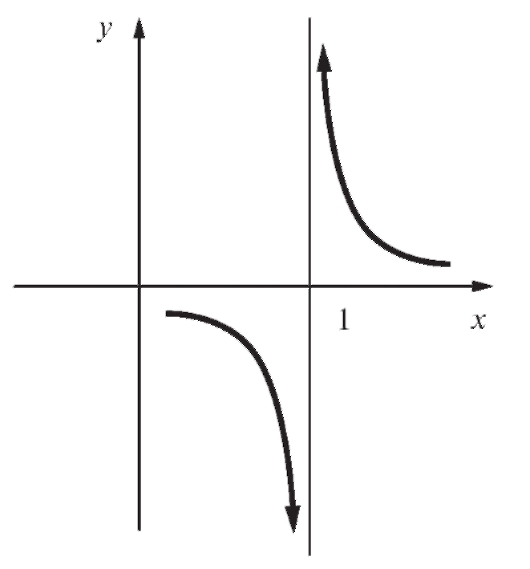
Рис. 2.11. Вертикальная асимптота для 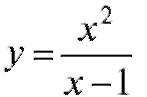 (схематически)
(схематически)
2.4. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
К ИССЛЕДОВАНИЮ ФУНКЦИИ
2.4.1. Признак постоянства функции. Признаки возрастания и убывания функций
Теорема 2.4. Для того чтобы функция y = f (x) была постоянна на некотором промежутке, необходимо и достаточно, чтобы на этом промежутке f ' (x) = 0.
Предположим теперь, что Тогда можно выделить ин-
Тогда можно выделить ин-
тервалы, в которых функция возрастает или убывает (см. п. 1.1.2). Теорема 2.5 (необходимый признак монотонности).
1) Если y = f (x) дифференцируема и возрастает на некотором промежутке, то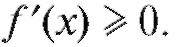
2) Если y = f (x) дифференцируема и убывает на некотором промежутке, то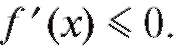
Теорема 2.6 (достаточный признак монотонности).
1) Если на некотором интервале (a; b) f (x) > 0, то f (x) возрастает на (a; b).
2) Если f'(x) < 0 на некотором интервале (a; b), то f (x) убывает на данном интервале.
Ранее мы останавливались на геометрическом смысле производной. Исходя из этого, утверждения теорем 2.5 и 2.6 могут быть проиллюстрированы геометрически. В любой точке промежутка возрастания функции y = f (x) касательная к ее графику образует острый угол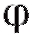 с осью Ox (рис. 2.12, а), на промежутке убывания функции угол
с осью Ox (рис. 2.12, а), на промежутке убывания функции угол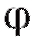 тупой (рис. 2.12, б). Таким образом, промежутку возрастания функции f (x) соответствует случай
тупой (рис. 2.12, б). Таким образом, промежутку возрастания функции f (x) соответствует случай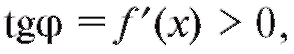 а промежутку убывания - случай
а промежутку убывания - случай
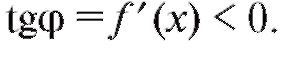
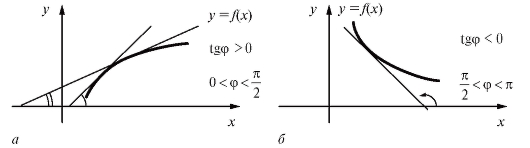
Рис. 2.12. Связь между монотонностью функции и углом наклона касательной: а - для возрастающей функции; б - для убывающей функции
Пример. Для функции y = x2 - 2x + 1 найти промежутки возрастания и убывания.
Решение. Область определения данной функции: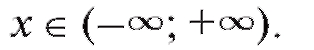 Найдем y' = 2x - 2 = 2(x - 1). Следовательно, y' < 0 при x < 1 и y' > 0 при x > 1.
Найдем y' = 2x - 2 = 2(x - 1). Следовательно, y' < 0 при x < 1 и y' > 0 при x > 1.
Таким образом, на интервале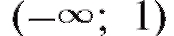 функция убывает, а при
функция убывает, а при
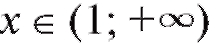 возрастает. В точке x = 1 убывание переходит в возрастание.
возрастает. В точке x = 1 убывание переходит в возрастание.
2.4.2. Экстремумы функции. Необходимое условие экстремума
Функция y = f (x) может убывать или возрастать не во всей своей области определения. Эта область часто распадается на промежутки, в одних из которых функция убывает, в других - возрастает.
Точка отделяющая промежуток возрастания от промежутка убывания и принадлежащая области определения функции, называется точкой экстремума.
Точки экстремума бывают двух типов (рис. 2.13): точки максимума функции, где функция переходит от возрастания к убыванию (точки x1 и и точки минимума (точки x2 и x4), где функция переходит от убывания к возрастанию.
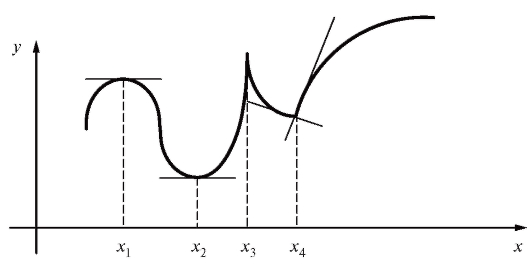
Рис. 2.13. Точки экстремума: x1 и x3 - точки максимума; x2 и x4 - точки минимума
В точках максимума величина f (x) больше, а в точках минимума - меньше, чем во всех соседних достаточно близких точках. Таким образом, логично ввести следующие определения.
Определение. Точка x0 называется точкой максимума функции y = f (x), если для любой точки x, принадлежащей достаточно малой окрестности точки x0,

и x0 - точка минимума, если в малой окрестности этой точки

Определение. Значения функции в точках максимума и минимума называются, соответственно, максимальным и минимальным значениями функции.
Отметим, что речь идет о локальных экстремумах, таких как M и m (рис. 2.14).
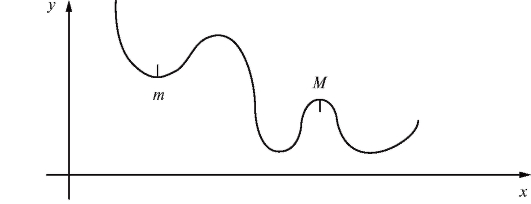
Рис. 2.14. Точки экстремума
Таким образом, максимум и минимум функции - это не наибольшее и наименьшее значение функции во всей области определения, а только максимальное или минимальное значения функции по сравнению со значениями функции во всех соседних, близких точках.
Теорема 2.7. Если y = f (x) дифференцируема в точке x0 и имеет в этой точке экстремум, то f ' (x0) = 0.
Эту теорему можно истолковать геометрически, используя вновь смысл производной: если в точке экстремума график функции y = f (x) имеет касательную и эта касательная не параллельна оси Oy (как для точки x3 на рис. 2.13), то эта касательная обязательно параллельна оси Ox (точки x1 и x2 на рис. 2.13).
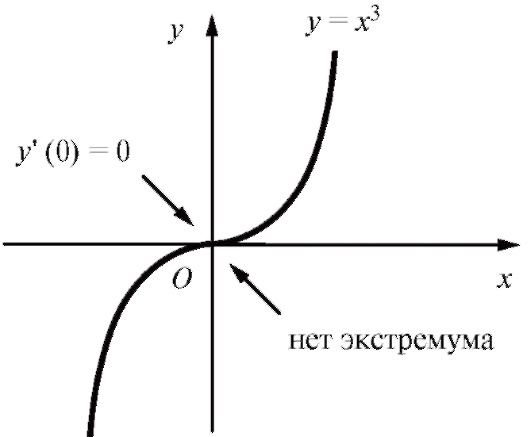
Рис. 2.15. Кубическая парабола
Кроме точек экстремума, где функция дифференцируема и где, как показано ранее,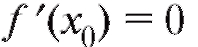 (точки x1 и x2 на рис. 2.13), могут быть такие
(точки x1 и x2 на рис. 2.13), могут быть такие
точки экстремума, где функция f (x) недифференцируема.
В точке x3 на рис. 2.13 - максимум (касательная параллельна оси ординат,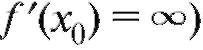 , в точке x4 - минимум (касательная к графику вообще не существует).
, в точке x4 - минимум (касательная к графику вообще не существует).
Из всего сказанного следует практическое правило: точки, в которых функция имеет экстремумы, надлежит искать среди точек, в которых:
1) либо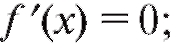
2) либо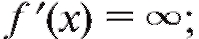
3) либо f' (x) не существует, причем предполагается, что точки эти принадлежат области определения функции.
Точки указанных типов называются критическими точками первого рода.
Отметим, что не в каждой критической точке функция имеет экстремум.
Пример. y = x3. Решение. y' = 3x2. Точка x = 0 будет для данной функции критической точкой первого рода, так как y' (0) = 0. Однако в этой точке экстремума нет (рис. 2.15).
Как же решить вопрос о наличии экстремума в критической точке? Ответ на этот вопрос мы найдем в следующем пункте.
2.4.3. Достаточное условие экстремума (по первой производной)
Теорема 2.8. Пусть x0 будет критической точкой первого рода для функции y = f (x). Тогда, если в окрестности точки x0 будет меняться знак производной, то точка x0 - точка экстремума, причем, если знак меняется с «+» на «-», то в точке x0 - максимум, если с «-» на «+», то минимум. Другими словами, если (рис. 2.16)
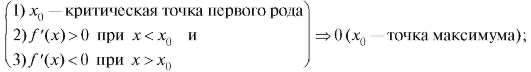
если (рис. 2.17)

Доказательство этой теоремы вытекает из теоремы 2.6 (так, если при x < x0 функция возрастает, а при x > x0 убывает, то в точке x0 функция переходит от возрастания к убыванию, т. е. x0 - точка максимума).
Заметим, что если при переходе через критическую точку f ' (x) не меняет знака, то в критической точке экстремума нет (см. пример с кубической параболой и рис. 2.18).
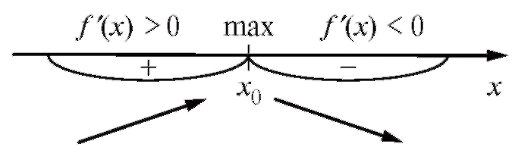
Рис. 2.16. Схема нахождения максимума
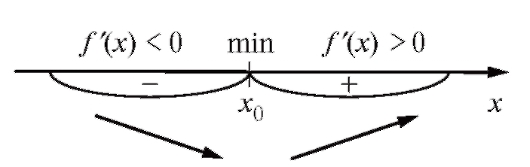
Рис. 2.17. Схема нахождения минимума
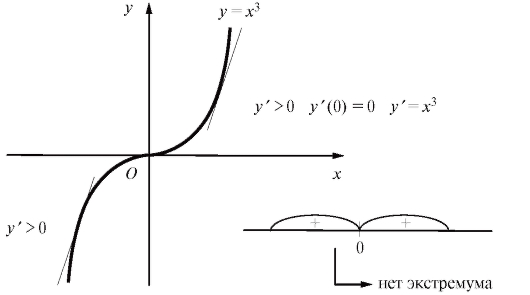
Рис. 2.18. График, иллюстрирующий отсутствие экстремума у кубической параболы
Пример 1. Для функции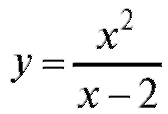 найти точки максимума и минимума.
найти точки максимума и минимума.
Решение. Функция не определена при x = 2.
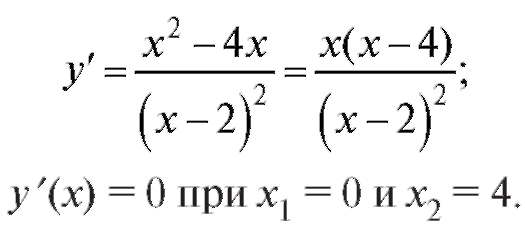
Нанесем на ось Ox точки, не принадлежащие области определения функции, а также критические точки первого рода. Тогда ось разобьется на 4 интервала, в каждом из которых исследуем знак у'.
Расставим эти знаки над интервалами. Тогда, согласно изложенной ранее теории, f (x) возрастает при 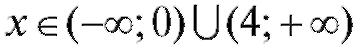 и убывает при
и убывает при
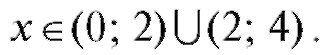 Так как в окрестности точки x1 = 0 знак y' поменялся с «+» на «-», то x1 = 0 - точка максимума, а в окрестности точки x2 = 4 знак у' изменился с «-» на «+», и, следовательно, x2 = 4 - точка минимума. Тогда
Так как в окрестности точки x1 = 0 знак y' поменялся с «+» на «-», то x1 = 0 - точка максимума, а в окрестности точки x2 = 4 знак у' изменился с «-» на «+», и, следовательно, x2 = 4 - точка минимума. Тогда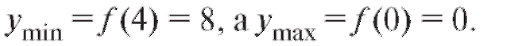
Пример 2. Дано уравнение прямолинейного движения точки x = 6t2 - t3 (t - в секундах, x - в метрах). Найти наибольшую скорость точки.
Решение. Скорость точки 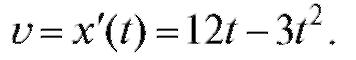 Исследуем, когда
Исследуем, когда
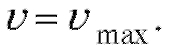 Итак, нужно найти наибольшее значение функции
Итак, нужно найти наибольшее значение функции
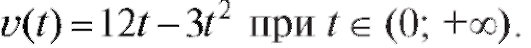
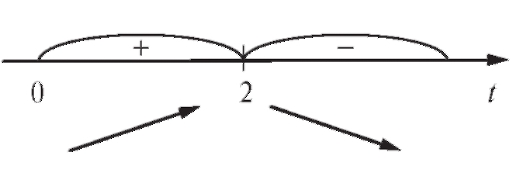
Рис. 2.19. Изменения знака производной скорости
На данном промежутке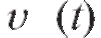 дифференцируема и
дифференцируема и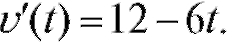 Найдем критические точки первого рода:
Найдем критические точки первого рода: 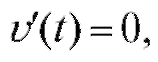 т. е. 12 - 6t = 0, откуда t = 2.
т. е. 12 - 6t = 0, откуда t = 2.
Так как в окрестности точки t = 2 изменился знак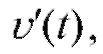 то в
то в
точке t = 2 - экстремум, причем изменение знака произошло с «+» на «-» и, следовательно, t = 2 - точка максимума (рис. 2.19).
Тогда 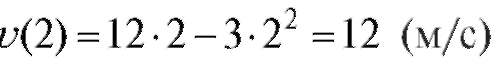 - максимальное значение скорости.
- максимальное значение скорости.
2.4.4. Выпуклость и вогнутость кривых
Определение. Кривая, являющаяся графиком функции у = f (x), называется выпуклой на некотором промежутке, если она целиком лежит под касательной, проведенной к ней в любой точке этого промежутка (рис. 2.20, а). Кривая называется вогнутой на некотором промежутке, если она целиком лежит над касательной, проведенной к ней в любой точке этого промежутка (рис. 2.20, б).
Если график выпуклый на промежутке, то приращение функции меньше ее дифференциала , а если вогнутый, то, наоборот,
, а если вогнутый, то, наоборот,
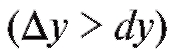 в любой точке x и для произвольного
в любой точке x и для произвольного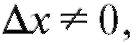 настолько малого
настолько малого
по модулю, чтобы точка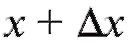 не вышла за пределы рассматриваемого
не вышла за пределы рассматриваемого
промежутка.
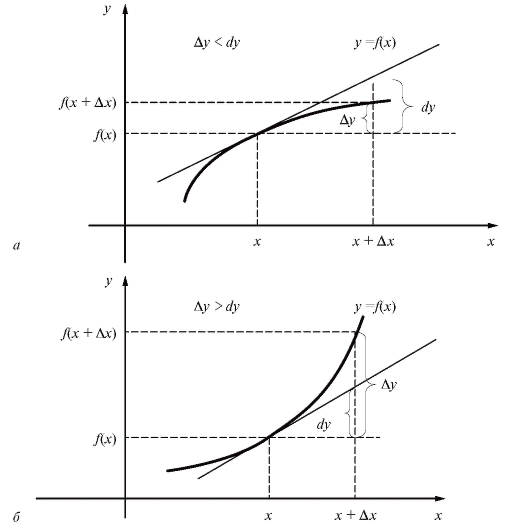
Рис. 2.20. Характер выпуклости кривых: а - кривая выпукла; б - кривая вогнута
Теорема 2.9. Если функция y = f (x) дважды дифференцируема на некотором промежутке и на данном промежутке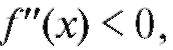 то график функции выпуклый, если же
то график функции выпуклый, если же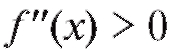 , график функции вогнутый на данном промежутке.
, график функции вогнутый на данном промежутке.
Пример. Дано 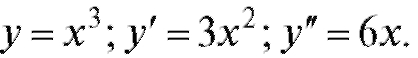 Определить, на каких проме-
Определить, на каких проме-
жутках функция выпукла, на каких - вогнута. Решение.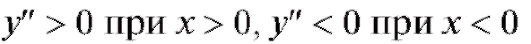
Следовательно, согласно последней теореме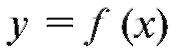 выпукла для
выпукла для
x < 0 и вогнута для x > 0.
2.4.5. Точки перегиба графика функции
График функции y = f (x) может быть выпуклым или вогнутым не во всей области определения этой функции. Область определения функции часто распадается на промежутки выпуклости и вогнутости (области I и II на рис. 2.21). Точки, отделяющие друг от друга промежутки выпуклости и вогнутости, называются точками перегиба функции. Геометрически это значит, что кривая лежит над касательной с одной стороны от точки перегиба и под касательной - с другой.
Аналогично определению критической точки первого рода можно ввести определение критической точки второго рода.
Точка x0, принадлежащая области определения функции, называется критической точкой второго рода, если в этой точке выполняется одно из трех условий:
1) либо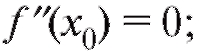
2) либо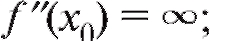
3) либо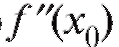 не существует.
не существует.
Точки перегиба следует искать среди критических точек второго
рода.
Утверждение. Если при переходе через критическую точку второго рода x0 вторая производная меняет знак, то точка x0 - точка перегиба.
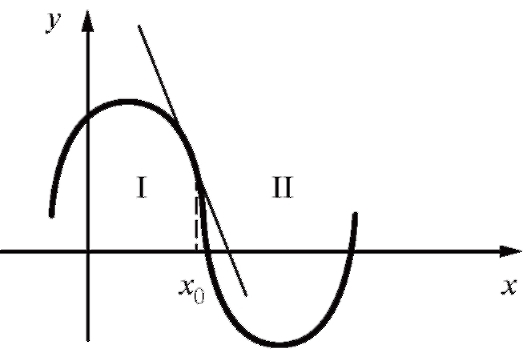
Рис. 2.21. Точки перегиба как границы промежутков выпуклости и вогнутости
Пример. Дано
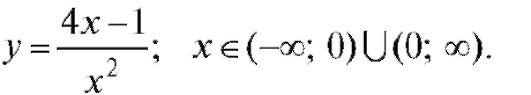
Решение.
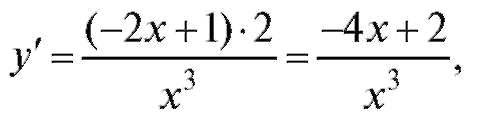
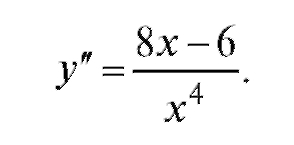
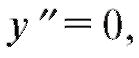 если
если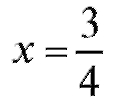 - критическая точка второго рода. На ось Ox нанесем
- критическая точка второго рода. На ось Ox нанесем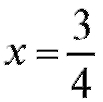 и выколем точку
и выколем точку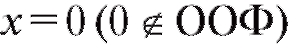 - рис. 2.22.
- рис. 2.22.

Рис. 2.22. Точки на оси Ox
В каждом из получившихся трех интервалов исследуем знак второй производной и расставим над интервалами соответствующие знаки.
В окрестности точкизнак y" изменился. Следовательно, это
точка перегиба.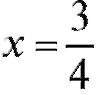
Итак, в п. 2.4.1-2.4.5 мы рассмотрели задачи об исследовании функций по первой и второй производным. Теперь объединим эти знания, чтобы строить графики функций.
2.4.6. Полная схема исследования функций с помощью производных и построения графиков
Знание промежутков возрастания (убывания) функции, промежутков выпуклости (вогнутости), точек экстремума, перегиба, а также асимптот позволяет иметь достаточно полное представление о характере поведения функции, что дает возможность построить ее график.
Для построения схематического графика функции удобно придерживаться следующего плана.
1. Выполнить элементарное исследование.
• Установить область определения функции.
• Найти точки пересечения графика с осями координат.
• Исследовать функцию на четность, отметив какую-либо симметрию графика (если она существует).
Напомним, что график четной функции симметричен относительно оси Ох, а график нечетной функции - относительно начала координат.
2. Найти асимптоты графика (см. п. 2.3.4).
3. Исследовать функцию по первой производной - промежутки монотонности, экстремумы (см. п. 2.4.1-2.4.3).
• Найти y'(x).
• Найти критические точки первого рода.
• На ось Ox нанести точки, не принадлежащие области определения функции (исключив их), а также критические точки первого рода.
Тогда ось Ox разобьется на ряд интервалов. В каждом из интервалов следует определить знак y'(x) (для этого достаточно найти знак y' в любой точке каждого интервала, поскольку внутри любого интервала знак y'(x) не меняется) и отметить полученные результаты над соответствующими интервалами. По знаку y'(x) найти интервалы возрастания и убывания. Выявить точки экстремумов функции (при переходе через такие точки y'(x) меняет знак). Напоминаем, что точки экстремума - это точки, которые обязательно принадлежат области определения функции!
• Вычислить значения функции в точках экстремума.
4. Исследовать функцию по второй производной - характер выпуклости и точки перегиба (см. п. 2.4.4 и 2.4.5).
• Найти y "(x).
• Найти критические точки второго рода.
• На ось Ox нанести точки, не принадлежащие области определения, а также критические точки второго рода.
• В каждом из получившихся интервалов определить знак y "(x).
• Найти точки перегиба (точки, в окрестности которых y "(x) меняет знак).
• Вычислить значения функции в точках перегиба.
5. Построить график по результатам исследования 1-4.
Отметим, что иногда для уточнения вида графика целесообразно вычислить дополнительно еще несколько значений функции в «обыкновенных» точках.
Изложенную схему проиллюстрируем следующим примером:
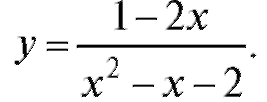
1. Элементарное исследование.
• Данная функция представляет собой дробь, а, значит, она не определена, если знаменатель x2 - x - 2 = 0.
Найдем корни знаменателя: x1 = -1, x2 = 2.
Следовательно, область определения функции имеет вид:
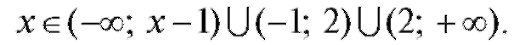
• Определим точки пересечения функции с осями координат. Пусть x = 0. Тогда y = -1/2, т. е. точка (0; -1/2) - точка пересечения графика с осью Oy.
Если y = 0, то 1 - 2x = 0 и, следовательно, x = -1/2. Точка (1/2; 0) - пересечение графика с осью Ох.
• Рассмотрим функцию при аргументе (-x):
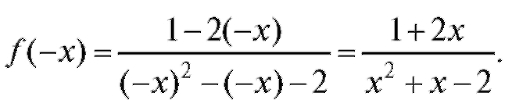
Очевидно,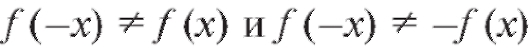 , а значит, y = f (x) -
, а значит, y = f (x) -
функция общего вида, и график ее не обладает симметрией ни относительно точки O (0; 0), ни относительно оси Oy. 2. Асимптоты.
Так как точки x = -1 и x = 2 не принадлежат области определения функции, то следует рассматривать предел функции при стремлении аргумента к данным точкам слева и справа от них.
Итак,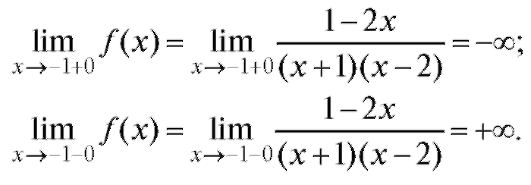
Тогда, по определению вертикальной асимптоты - x = -1 - уравнение вертикальной асимптоты имеет вид: x = 2, так как
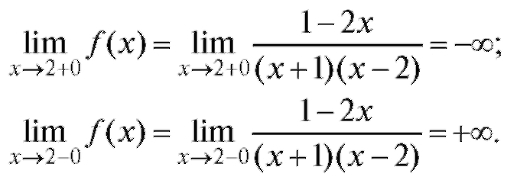
Теперь рассмотрим вопрос о существовании наклонных (горизонтальных) асимптот. Вычислим
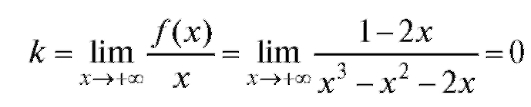
(по правилу Лопиталя). Тогда
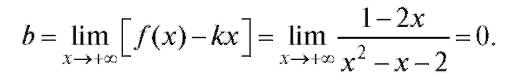
Итак, при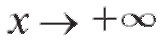 мы получим: k = 0, b = 0, и, следовательно, суще-
мы получим: k = 0, b = 0, и, следовательно, суще-
ствует горизонтальная асимптота y = 0.
Аналогичным образом, при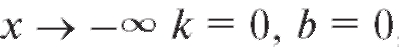 , а значит, y = 0 -
, а значит, y = 0 -
уравнение горизонтальной асимптоты и при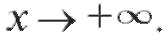 Наклонных
Наклонных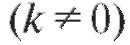
асимптот у графика нет.
3. Исследование функции по y'(x). Вычислим y'(x) по правилу дифференцирования дробей:
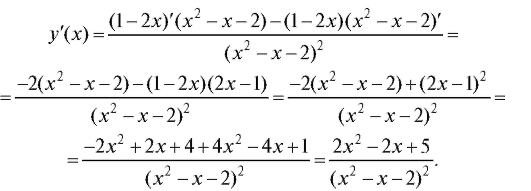
Приравняем уравнение y'(x) к нулю. Тогда 2x2 - 2x + 5 = 0. Но дискриминант этого уравнения отрицателен, и, следовательно, корней нет. Значит, критических точек первого рода нет, и на ось Ox нанесем только те точки, которые не принадлежат области определения функции (рис. 2.23).
В каждом из интервалов рассмотрим знак y'(x) - рис. 2.24. Таким образом, во всех получившихся интервалах функция возрастает, а точек экстремума нет.
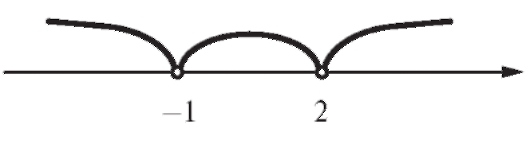
Рис. 2.23. Выколотые точки
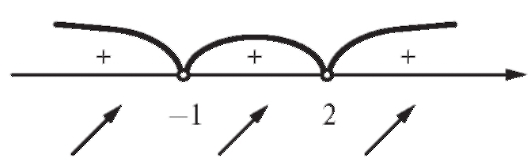
Рис. 2.24. Знак производной
4. Исследование функции по y"(x). Вычислим
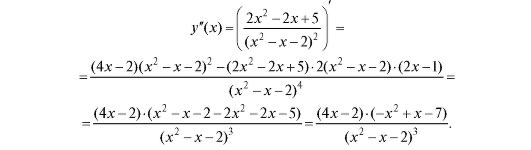
Найдем критические точки второго рода. Определим корни уравнения y "(x) = 0:
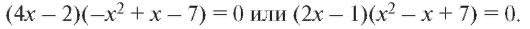
Первая скобка равна нулю, если x = 1/2, а вторая в 0 не обращается.
Итак, x = 1/2 - критическая точка второго рода.
Нанесем эту точку, а также точки x = -1 и x = +2 (которые не принадлежат области определения функции) на ось Ох.
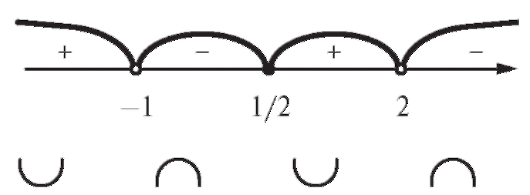
Рис. 2.25. Направления выпуклости
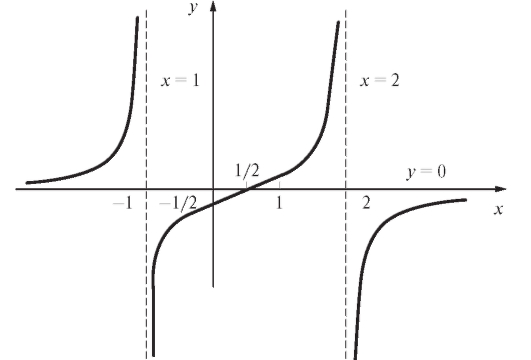
Рис. 2.26. График функции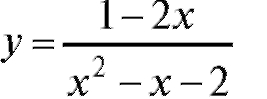
В каждом из полученных интервалов определим знак y "(x), а также направление выпуклости (рис. 2.25).
Итак, функция вогнута при x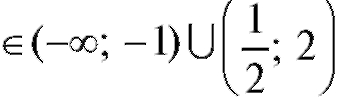 и выпукла при
и выпукла при
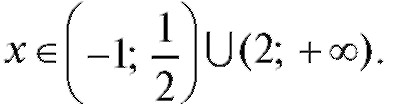 Точки x = -1 и x = +2 не являются точками перегиба (они не принадлежат ООФ), а x = 1/2 - точка перегиба. Найдем f (1/2). Построим график y = f (x) - рис. 2.26.
Точки x = -1 и x = +2 не являются точками перегиба (они не принадлежат ООФ), а x = 1/2 - точка перегиба. Найдем f (1/2). Построим график y = f (x) - рис. 2.26.
Самостоятельная работа
Построить график функции (1-20).