Математика : учебник / И. В. Павлушков, Л. В. Розовский, И. А. Наркевич. - 2013. - 320 c. : ил.
|
|
|
|
Глава 1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
1.1. ФУНКЦИИ
1.1.1. Определение функции, числовых промежутков и окрестности точек
Одним из основных математических понятий является понятие функции, устанавливающее зависимость между элементами двух множеств.
Определение. Пусть Х, Y - некоторые множества, элементами которых являются некоторые числа. Если каждому числу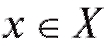 по некоторому закону или правилу f ставится в соответствие число
по некоторому закону или правилу f ставится в соответствие число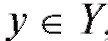 то говорят, что на множестве Х задана числовая функция f, и записывают эту функциональную зависимость формулой y = f (x) или, более наглядно, в виде диаграммы:
то говорят, что на множестве Х задана числовая функция f, и записывают эту функциональную зависимость формулой y = f (x) или, более наглядно, в виде диаграммы:

Переменная x называется независимой переменной или аргументом, а переменная y - зависимой переменной (от x) или функцией.
Множество X - область изменения аргумента - называется областью определения функции (ООФ). Множество Y, содержащее все значения, которые принимает y, называется областью изменения функции.
При дальнейшем изложении множества X и Y часто оказываются конечными или бесконечными промежутками.
Конечные промежутки:
• открытый интервал, или просто интервал (a; b) - множество вещественных чисел, удовлетворяющих неравенствам a < x < b, или (a; b)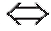 (a < x < b), где о - знак эквивалентности;
(a < x < b), где о - знак эквивалентности;
• замкнутый интервал (или отрезок) [a; b]: [a; b] (a < x < b);
(a < x < b);
• полуоткрытые интервалы (a; b] и [a; b): (a; b]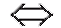 (a < x < b) и [a; b)
(a < x < b) и [a; b)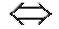 (a < x < b) соответственно.
(a < x < b) соответственно.
Бесконечные промежутки:
• 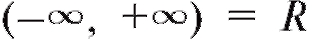 - множество всех вещественных чисел, т. е.
- множество всех вещественных чисел, т. е.  ; аналогично,
; аналогично,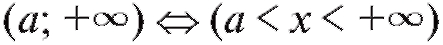 и т. д.
и т. д.
Числа a, b называются соответственно левым и правым концами этих промежутков.
Символы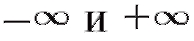 - не числа, а обозначение процесса неограни-
- не числа, а обозначение процесса неограни-
ченного удаления точек числовой оси влево и вправо от начала 0.
Пусть х0 - любое действительное число (точка на числовой прямой). Окрестностью точки х0 называется любой интервал (a; b), содержащий точку х0, интервал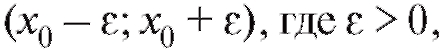 симметричный относительно
симметричный относительно
называется е-окрестностью точки х0 (рис. 1.1).

Рис. 1.1. е-окрестность точки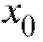
Если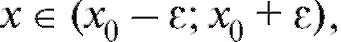 то справедливы неравенства
то справедливы неравенства
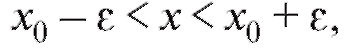
что равносильно
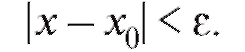
Частное значение функции f (x) при x = а можно найти, подставив а вместо аргумента: f (a). При этом а может быть как буквенным выражением, числом, так и некоторой функцией, например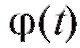 . В последнем случае
. В последнем случае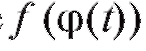 будет сложной функцией, с ней мы ознакомимся в п. 1.1.3.
будет сложной функцией, с ней мы ознакомимся в п. 1.1.3.
Пример 1. Найти область определения и область значений функции
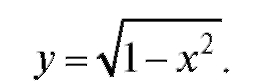
Решение. Область определения этой функции состоит из всех x, для которых она имеет смысл. Таким образом,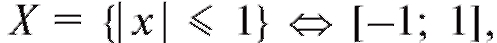
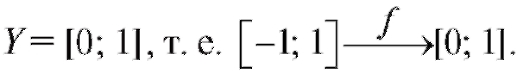
Пример 2. Найти область определения и область значений функции
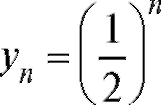
Решение. Здесь независимая переменная n принимает целые положительные значения n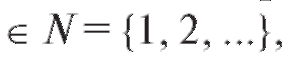 следовательно, y является функцией натурального аргумента и вычисляется по заданной формуле
следовательно, y является функцией натурального аргумента и вычисляется по заданной формуле
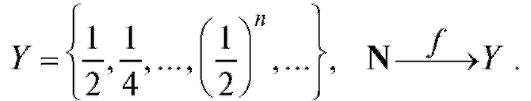
Пример 3. При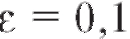 постро-
постро-
ить е-окрестность точки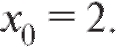
Решение. По определению е-окрестностью точки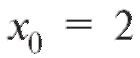 бу-
бу-
дет интервал | x - 2| < 0,1 или -0,1 < x - 2 < 0,1 1,9 < x < 2,1 (рис. 1.2).
1,9 < x < 2,1 (рис. 1.2).
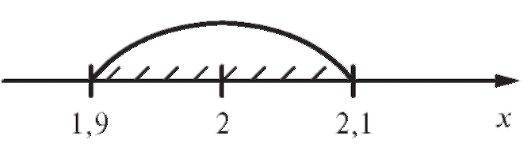
Рис. 1.2. Интервал |x - 2| < 0,1
Самостоятельная работа
1. Построить интервалы изменения переменной x, удовлетворяющей неравенствам:

2. Найти области определения функций:
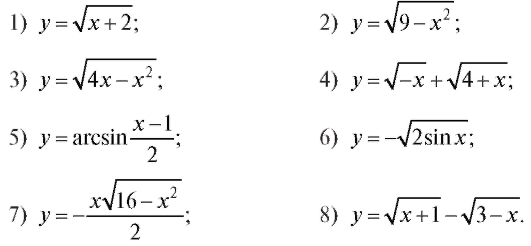
3. Вычислить значения функций в заданных точках:
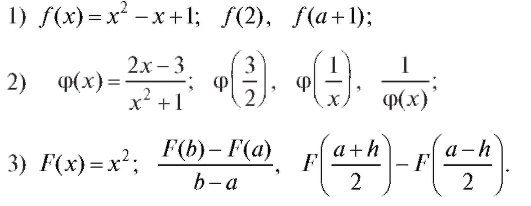
1.1.2. Некоторые свойства функций и их графиков
Пусть задана функция f : X → Y. Правило, по которому можно находить y, зная x, может быть задано графиком функции.
Определение. Графиком функции в декартовой прямоугольной системе координат называется множество всех точек, абсциссы которых являются значениями аргумента, а ординаты - соответствующими значениями функции.
Пример 1. Графиком функции y = x2 является парабола, ось симметрии которой совпадает с положительной полуосью ординат, а вер-
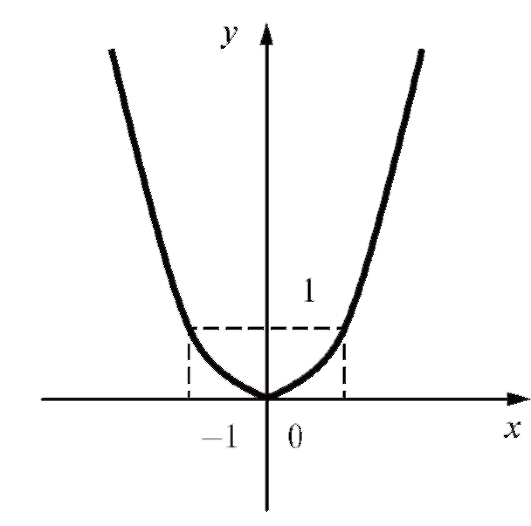
Рис. 1.3. График функции y = x2
шина - с началом координат (рис. 1.3).
Часто графики автоматически вычерчиваются самопишущими приборами или изображаются на экране дисплея. Преимуществом такого представления функции является наглядность, а недостатком - неточность.
Функцию можно задавать также с помощью таблицы или формулы (аналитически). Табличный способ применяется на практике при обработке результатов наблюдений приближенных значений функции. Аналитический способ
задания функции является наиболее удобным для полного исследования функции при помощи методов математического анализа.
Отметим основные характеристики функции: монотонность, ограниченность, четность (нечетность), периодичность.
Определение. Функция называется возрастающей (убывающей) в интервале, если большему значению аргумента из этого интервала соответствует большее (меньшее) значения функции.
График возрастающей на интервале (a; b) функции, если его рассматривать слева направо, поднимается вверх (рис. 1.4, а), а для убывающей функции - опускается вниз (рис. 1.4, б).
Определение. Интервал независимой переменной, в котором функция возрастает (убывает), называется интервалом возрастания (убывания). Как интервал возрастания, так и интервал убывания называют интервалами монотонности функции, а функцию в этом интервале - монотонной функцией.
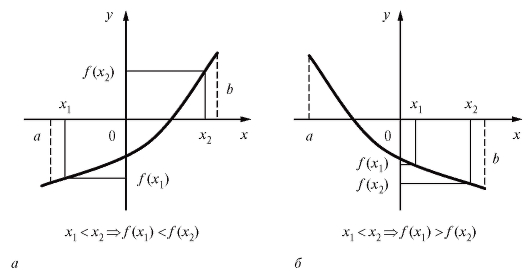
Рис. 1.4. График: а - возрастающей функции на интервале (a; b); б - убывающей функции на интервале (a; b)
Определение. Значение аргумента, при котором функция обращается в ноль, называется нулем функции.
Если функция задана формулой y = f (x), то для нахождения нуля (или нулей) функции следует решить уравнение f (x) = 0.
При графическом задании нулями функции являются точки пересечения ее графиком оси абсцисс.
Пример 2. Найти нули функции y = 2x + 1.
Решение.
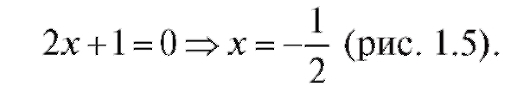
Определение. Функция называется четной, если при изменении знака допустимого аргумента значение функции не изменяется. Функция называется нечетной, если при изменении знака допустимого аргумента значение функции меняет знак на противоположный.
Таким образом, если функция f (x) - четная, то для всех x из ее
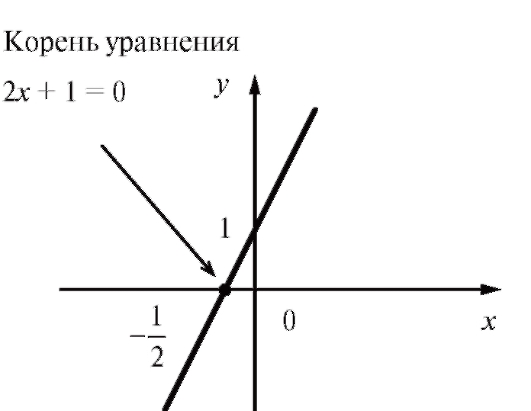
Рис. 1.5. График функции y = 2x + 1
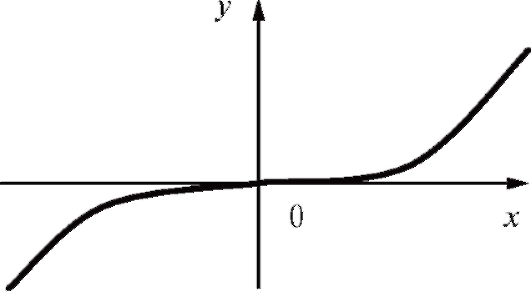
Рис. 1.6. График функции y = x3
области определения должно выполняться равенство f (-x) = f (x), как это происходит, например, при f (x) = x2, а если f (x) - нечетная, то f (-x) = -f (x) для любого x из области определения функции, как, например, в случае f (x) = x3.
Обратите внимание на то, что четные или нечетные функции должны быть обязательно определены в области, симметричной относительно начала координат.
При этом график четной функции симметричен относительно оси ординат (как на рис. 1.3), а график нечетной функции симметричен относительно начала координат (как на рис. 1.6).
Заметим, что не все функции являются четными либо нечетными; такие функции (не являющиеся ни четными, ни нечетными) будем называть функциями общего вида. Определение. Функция f (x), определенная на множестве Х, называется ограниченной на этом множестве, если существует такое число М > 0, что для всех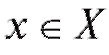 выполняется неравенство f (x)| < M.
выполняется неравенство f (x)| < M.
График ограниченной функции лежит между прямыми y = M и y = - M (рис. 1.7).
Определение. Функция f (x) называется периодической, если существует такое положительное число a, что f (x + a) = f (x) = f (x - a) для любого x из ООФ (точек x, x + a, x - a, принадлежащих области определения функции). При этом наименьшее положительное а с таким свойством (если таковое существует) называется периодом функции.
График периодической функции получается путем повторения части графика, соответствующего интервалу оси абсцисс, равному по длине периоду функции.
Примером периодической функции служит определенная на всей оси функция y = cos x, период которой равен 2π (рис. 1.8).
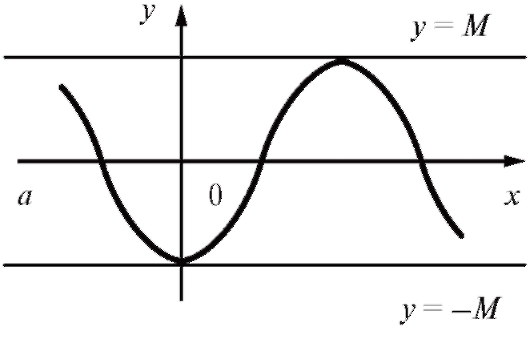
Рис. 1.7. График ограниченной функции
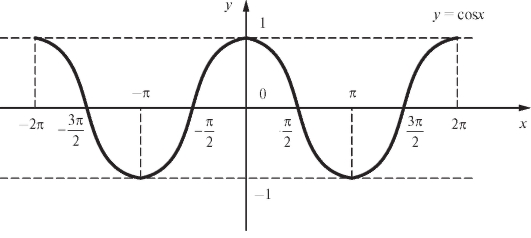
Рис. 1.8. График функции y = cos x
Таким образом, сдвиг графика периодической функции вдоль оси абсцисс на интервал, длина которого кратна периоду, не приводит к изменению этого графика. В частности область определения периодической функции не ограничена.
Самостоятельная работа
1. Указать, какие из следующих функций четные и какие нечетные:
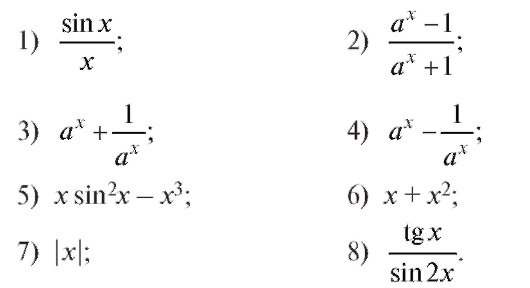
2. Найти нули функции:
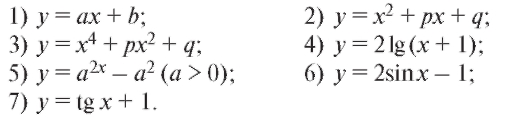
3. Найти период функции:
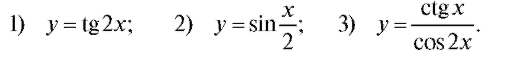
4. Воспользовавшись свойствами графиков четных/нечетных функций и результатами п. 1.1.2, построить графики функций:
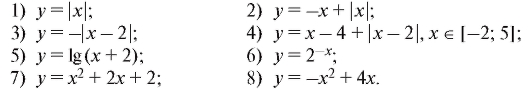
1.1.3. Сложная функция. Обратная функция
Определение. Сложной функцией (рис. 1.9) называется функция, аргумент которой также является функцией, т. е.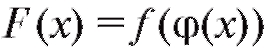 , или, в виде диаграммы, аналогично формуле (1.1).
, или, в виде диаграммы, аналогично формуле (1.1).
Иначе говоря, чтобы сосчитать значение в точке x сложной функции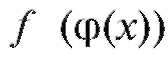 , составленной
, составленной
из функций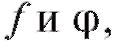 следует сначала найти частное значение
следует сначала найти частное значение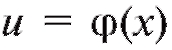 внутренней функции
внутренней функции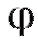 , а затем подставить его в качестве аргумента во внешнюю функцию f.
, а затем подставить его в качестве аргумента во внешнюю функцию f.
При этом область определения функции F (x) следует выбирать таким образом, чтобы промежуточное множество U, с одной стороны, было областью значений функции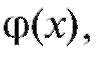 а с другой стороны, являлось областью определения функции f (u).
а с другой стороны, являлось областью определения функции f (u).
Пример 1. Рассмотрим сложную функцию y = lg (1 - x2). Здесь y = f (u) = lg u, в то время как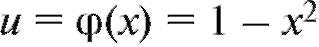 . Областью определения
. Областью определения
функции y является интервал (-1, 1), в котором как функция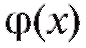 , так и функция
, так и функция 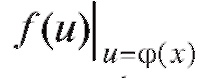 имеют смысл.
имеют смысл.
Рассмотрим функцию с областью определения Х и областью значений Y. Предположим, что каждому значению y е Y соответствует одна определенная точка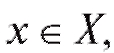 такая, что y = f (x). Тогда существует функция
такая, что y = f (x). Тогда существует функция 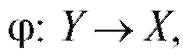 переводящая любое
переводящая любое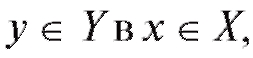 удовлетворяющее вышеука-
удовлетворяющее вышеука-
занному свойству y = f (x).
Функции f и ф с вышеперечисленными свойствами называются взаимно-обратными, а функция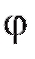 называется обратной по отношению к f. С учетом того, что символ x соответствует, как правило, независимой переменной, обычно вместо записи
называется обратной по отношению к f. С учетом того, что символ x соответствует, как правило, независимой переменной, обычно вместо записи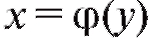 используют запись
используют запись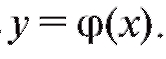
Из определения обратной функции вытекает, что любая строго монотонная функция имеет обратную.
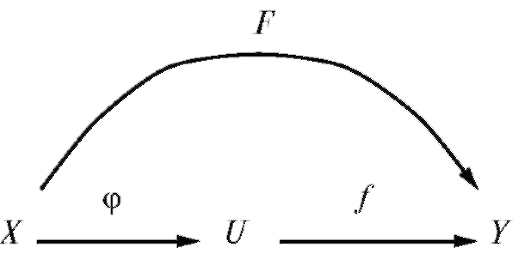
Рис. 1.9. Сложная функция
Между графиками функций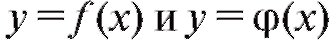 имеется простая связь:
имеется простая связь:
график обратной функции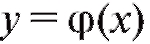 симметричен графику данной функ-
симметричен графику данной функ-
ции y = f (x) относительно биссектрисы I и III координатных углов.
Отметим, что взаимно-обратные функции f и ф удовлетворяют соотношению и могут с помощью него вычисляться:

Пример 2. Пусть y = f (x) = x3. Тогда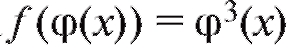 и равенство (1.2)
и равенство (1.2)
дает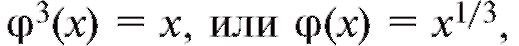 что, впрочем, легко следует непосред-
что, впрочем, легко следует непосред-
ственно из соотношения y = x3 (рис. 1.10).
Важно иметь в виду, что функция f (x), возрастающая или убывающая на Х, заведомо имеет обратную функцию (определение возрастания и убывания функции дано в п. 1.1.2).
В противоположном случае однозначность соответствия между X и Y нарушается, и обратной функции не существует. Однако, как правило, область определения Х можно разбить на участки возрастания и убывания функции f (x), на каждом из которых обратная функция уже может быть определена.
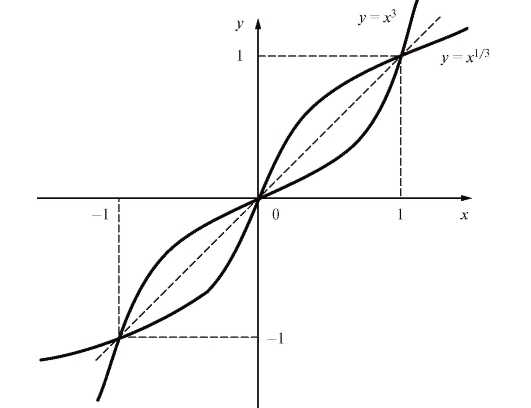
Рис. 1.10. Графики взаимно-обратных функций y = x3 и y = x1/3
Пример 3. Пусть y = x2. Тогда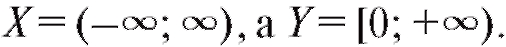 Таким обра-
Таким обра-
зом, взаимно однозначного соответствия между X и Y нет (каждому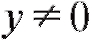 соответствуют два значения x, отличающиеся знаками), следовательно, нет и обратной функции (рис. 1.11).
соответствуют два значения x, отличающиеся знаками), следовательно, нет и обратной функции (рис. 1.11).
Если же разбить Х на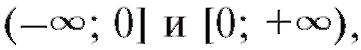 то на каждой полупрямой
то на каждой полупрямой
зависимость y = x2 является взаимно-однозначной, и, следовательно, на
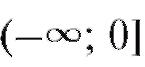 функция y = x2 имеет обратную функцию
функция y = x2 имеет обратную функцию 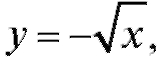 а на
а на 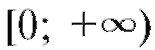 обратной к ней является
обратной к ней является
функция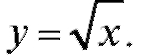
Пример 4. Пусть функция y связана с независимой переменной x линейной зависимостью 3x + 2y - 6 = 0. Найти обратную функцию и построить графики прямой и обратной функций.
Решение. Для нахождения обратной функции в общей с прямой функцией системе координат достаточно в соответствующем уравнении поменять обозначения x и y местами.
Таким образом, в нашем примере обратная зависимость выражается соотношением 3y + 2x - 6 = 0 и также является линейной.
При построении графиков (рис. 1.12) принималось во внимание то, что прямая линия однозначно определяется любой парой различных лежащих на ней точек. В частности прямая 3x + 2y - 6 = 0 определяется точками (0; 3) и (2; 0).
Заметим, что в соответствии со свойствами взаимно-обратных функций прямые на рис. 1.12 симметричны относительно биссектрисы I и III координатных углов.
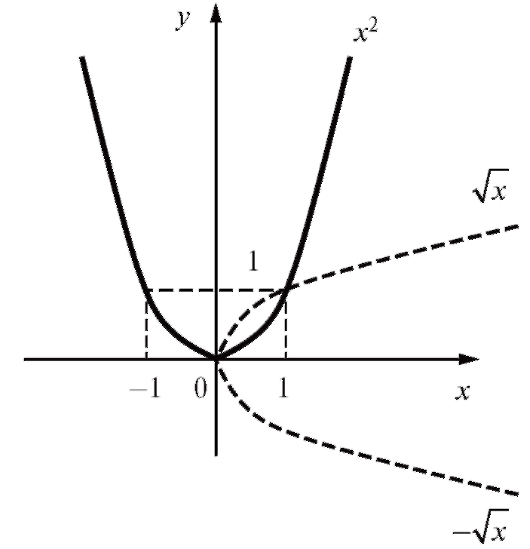
Рис. 1.11. Пример функции, не имеющей взаимно-обратной
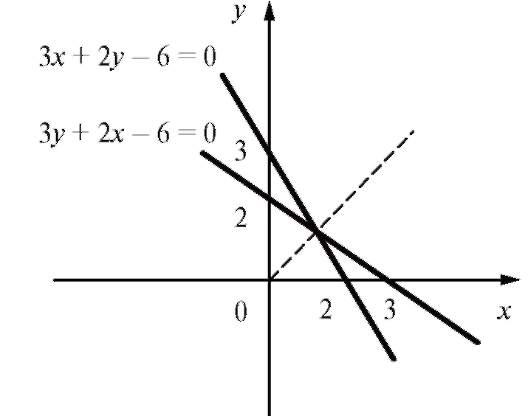
Рис. 1.12. Графики взаимно-обратных линейных функций
1.1.4. Элементарные функции
Определение. Основными элементарными функциями называются:
1) степенная функция: y = xn, где n - действительное число, x > 0 (в некоторых случаях, в частности при натуральном n, степенная функция определена на всей оси);
2) показательная функция: y = ax, где a > 0, а ^ 1, и X = R;
3) логарифмическая функция: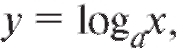 где основание логарифмов
где основание логарифмов
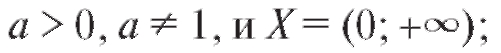
4) тригонометрические функции: y = sin x, y = cos x, y = tg x и y = ctg x;
5) обратные тригонометрические функции: y = arcsin x, y = arccos x, y = arctg x и y = arcctg x.
К множеству элементарных функций относятся все основные элементарные функции и постоянные, а также все функции, получающиеся из них с помощью четырех арифметических действий и операции взятия функции от функции, примененных последовательно конечное число раз.
Так, элементарными являются функции 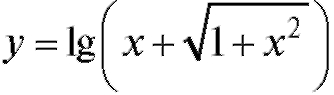 ,
,
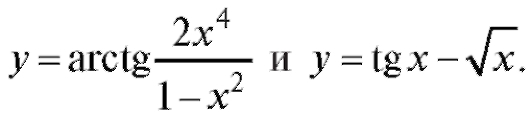 Функция
Функция
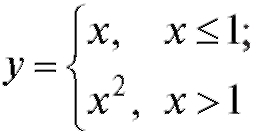
элементарной не является.
Областью определения элементарной функции являются все значения аргумента, при котором эта функция имеет смысл.
Например, областью определения функции 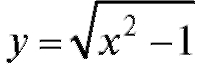 является
является
множество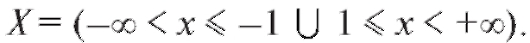 Здесь символ U обозначает
Здесь символ U обозначает
объединение.
Рассмотрим степенную и показательную функции. Степенная функция y = xn при целом n определена на всей оси; четная, если n - четное, и нечетная, если n - нечетное (см. рис. 1.2 и 1.5).
При произвольном n функция рассматривается в области x > 0. Если n > 0, то графики функции y = xn возрастают от нуля до бесконечности в интервале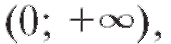 проходят через точки (0; 0) и (1; 1) и разделяют-
проходят через точки (0; 0) и (1; 1) и разделяют-
ся прямой y = x на кривые, обращенные выпуклостью вниз при n > 1 и вверх при 0 < n < 1 (рис. 1.13, а).
Если n < 0, то график функции
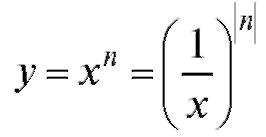 убывает от бесконечности до нуля (рис. 1.13, б).
убывает от бесконечности до нуля (рис. 1.13, б).
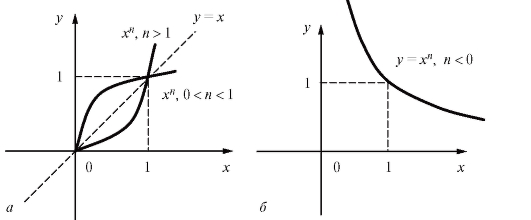
Рис. 1.13. График функции y = xn: а - для n > 0; б - для n < 0
Обратной к функции y = xn, x > 0, является функция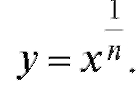 Напоминаем, что
Напоминаем, что
(n и m - целые положительные числа) и, в частности,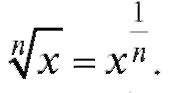
Показательная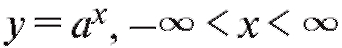 , и логарифмическая y = loga x, x > 0,
, и логарифмическая y = loga x, x > 0,
функции при одном и том же параметре a являются взаимно-обратными. Их графики симметричны относительно биссектрисы I и III координатных углов (рис. 1.14).
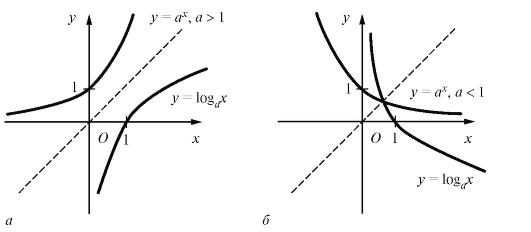
Рис. 1.14. Графики показательной и логарифмической функций: а - для a > 0;
б - для a < 0
Показательная функция всегда положительна, поэтому ее график расположен над осью Ox. Кроме того, поскольку a = 1, он проходит через точку (0; 1). При a > 1 показательная функция возрастает от нуля до бесконечности, при a < 1 - убывает от бесконечности до нуля. Отметим, что график показательной функции с основанием a симметричен относительно оси Oy графику показательной функции с основанием
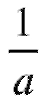 , что следует из равенства
, что следует из равенства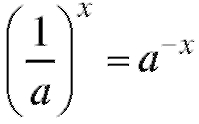 (рис. 1.15).
(рис. 1.15).
Напоминаем, что функция 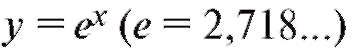 называется экспоненциальной, а ее график-экспонентой; логарифмы с основанием е обозначают через ln x и называют натуральными. Логарифмы с основанием 10 обозначают через lg x и называют десятичными. Таким образом,
называется экспоненциальной, а ее график-экспонентой; логарифмы с основанием е обозначают через ln x и называют натуральными. Логарифмы с основанием 10 обозначают через lg x и называют десятичными. Таким образом,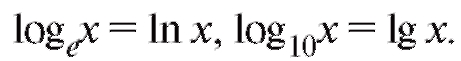
Принимая во внимание, что логарифмическая и показательная функции взаимно-обратны, имеем (см. (1.2)) 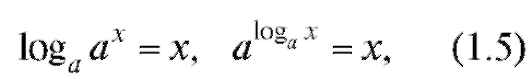
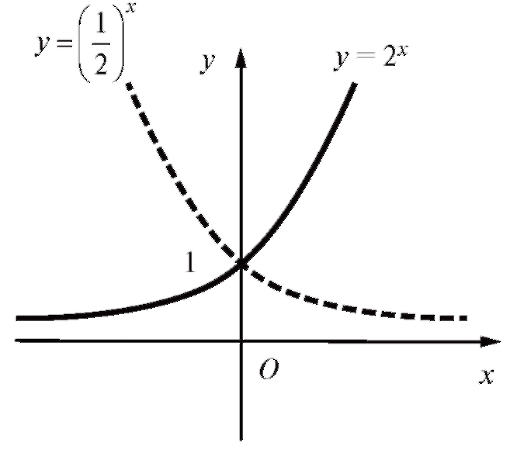
Рис. 1.15. Графики функций y = 2x и
y = 2-x
где первое равенство справедливо при любом x, а второе - при x > 0. В частности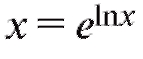 и, следовательно (см. (1.3)),
и, следовательно (см. (1.3)),

представление степенной функции с помощью показательной. Справедлива формула

т. е. логарифмы чисел при разных основаниях (a и b соответственно) пропорциональны друг другу с коэффициентом пропорциональности
(модулем перехода)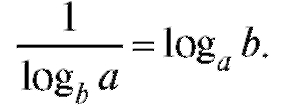
Пример 1. Выразить log2x через lg x и через ln x. Решение.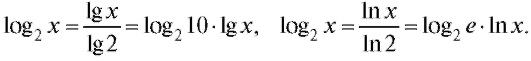
Пример 2. Записать функцию y = 2x в виде показательной функции с основанием 10. x Решение.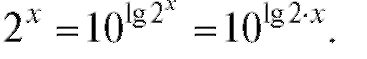
1.1.5. Тригонометрические функции
Прежде всего, напомним, что в качестве аргумента тригонометрических функций в математическом анализе всегда принимается радианная мера дуги или угла, т. е. число, равное отношению длины этой дуги к радиусу окружности. Таким образом,
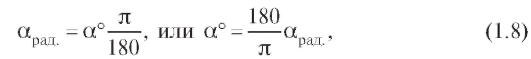
где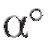 - градусная, а
- градусная, а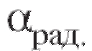 - радианная мера угла. В частности
- радианная мера угла. В частности
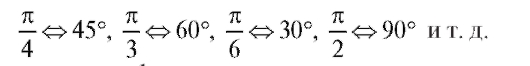
Тригонометрические функции являются периодическими: sin x и cos x имеют период 2π (рис. 1.16), а tg x и ctg x - период π (рис. 1.17).
График косинусоиды отличается от графика синусоиды сдвигом влево по оси Ox на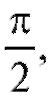 поскольку
поскольку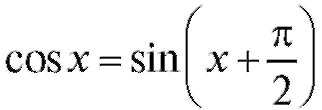 (см. п. 1.1.2).
(см. п. 1.1.2).
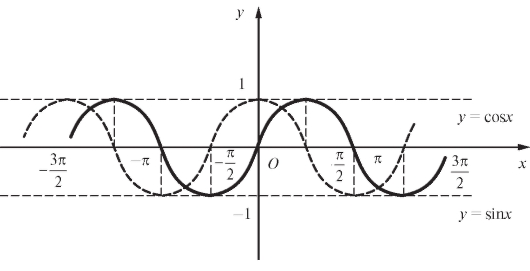
Рис. 1.16. Графики функций y = sin x и y = cos x
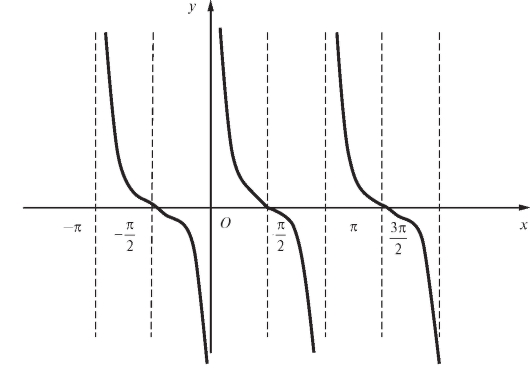
Рис. 1.17. График функции y = ctg x
Функции sin x, tg x и ctg x являются нечетными, а функция cos x - четная. Наконец, sin x и cos x определены при любом x, tg x - при всех x,
кроме точек вида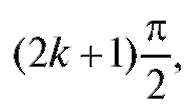 где k - любое целое число, а ctg x - при всех
где k - любое целое число, а ctg x - при всех
x, кроме точек вида kπ. Напоминаем, что
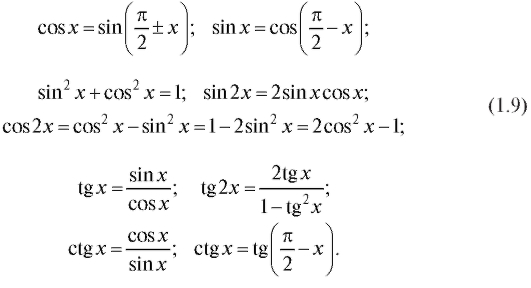
1.1.6. Обратные тригонометрические функции
Поскольку тригонометрические функции являются периодическими, каждому значению функции соответствует бесчисленное множество значений аргумента. Таким образом, взаимно-однозначного соответствия между x и y нет, и, следовательно, однозначная обратная функция не может быть определена.
Для решения проблемы нахождения x по y в случае зависимости y = sin x поступают следующим образом.
Функция y = sin x на интервале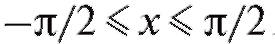 является возрастающей
является возрастающей
(рис. 1.18) и, следовательно, имеет обратную функцию, обозначаемую через y = arcsin x.
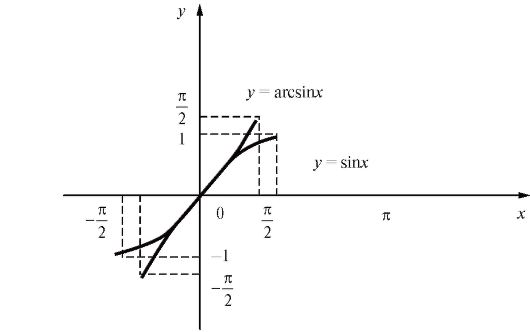
Рис. 1.18. График функции y = arcsin x
Учитывая, что график обратной функции симметричен с графиком прямой функции относительно биссектрисы I и III координатных углов, находим график функции arcsin x.
Областью определения Х функции y = arcsin x является отрезок [-1; 1], а областью ее значений Y - отрезок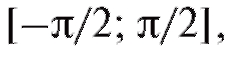 т. е.
т. е.
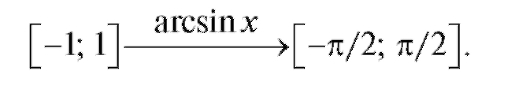
Кроме того, y = arcsin x является нечетной и возрастающей функцией.
Значение функции arcsin x есть радианная мера угла, синус которого равен данному значению независимой переменной x; при этом из всех углов, удовлетворяющих этому условию, выбирается угол из отрезка
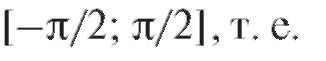
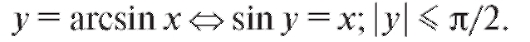 (1.10)
(1.10)
Все значения y, удовлетворяющие уравнению sin y = x, находят по формуле
k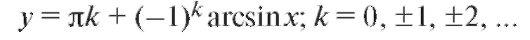 (1.11)
(1.11)
Например, решением уравнения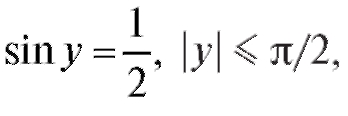 является
является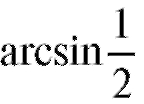 ,
,
т. е. число п/6. Общим же решением уравнения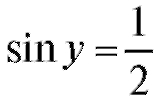 будут числа
будут числа
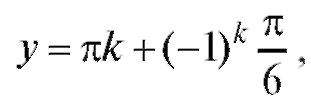 или числа
или числа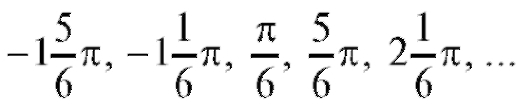
Функция, обратная к y = cos x, определяется аналогично. Имеем
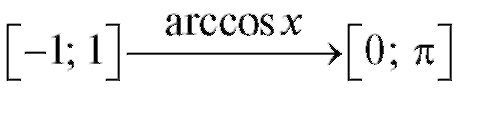
или
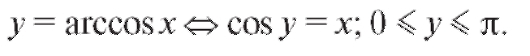
Функция y = arccos x убывает (рис. 1.19) и удовлетворяет равенству
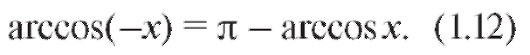
Общее решение уравнения cos y = x, | x | < 1, имеет вид
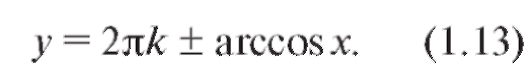
Отметим формулы:
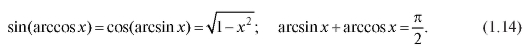
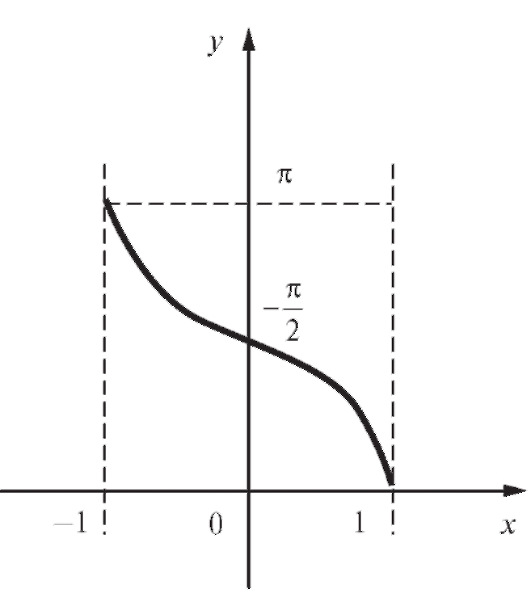
Рис. 1.19. График функции y = arccos x
Функция y = arctg x определена на всей оси; область ее значений - открытый интервал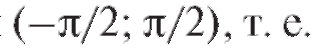
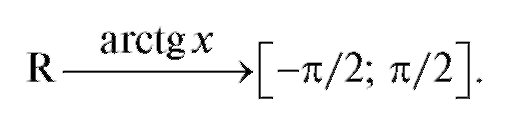
Эта функция является возрастающей и нечетной (рис. 1.20). Уравнению tg y = x удовлетворяют числа вида
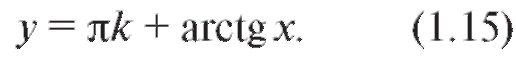
Аналогично функция y = = arcctg x определена на всей оси и принимает значения в интервале (0; п). Она убывает (рис. 1.21) и удовлетворяет равенству
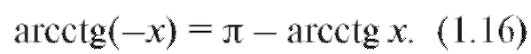
Общее решение уравнения ctg y = x имеет вид
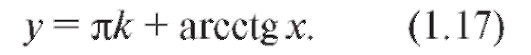
Отметим формулы: 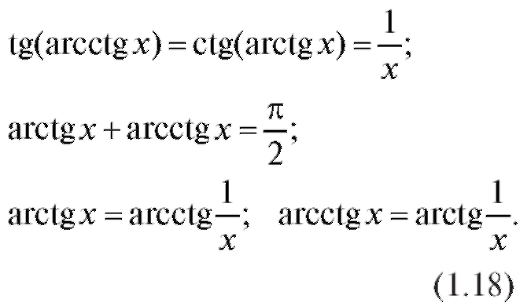
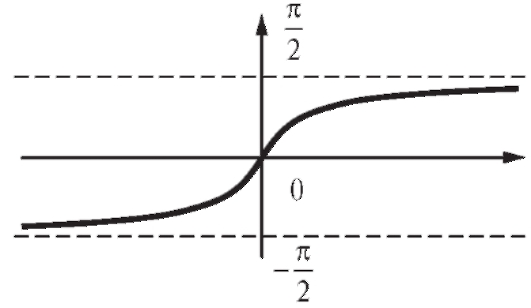
Рис. 1.20. График функции y = arctg x
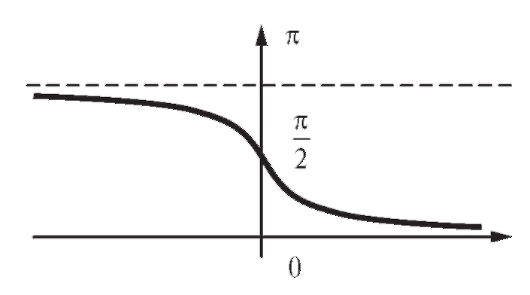
Рис. 1.21. График функции y = arcctg x
1.2. ПРЕДЕЛЫ
1.2.1. Предел функции
Теория пределов играет основополагающую роль в математическом анализе. С ее помощью устанавливаются такие свойства функции, как непрерывность, дифференцируемость, интегрируемость и т. д.
Рассмотрим пример. Пусть задана функция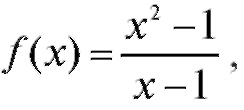 определен-
определен-
ная для всех x, кроме x = 1. Исследуем поведение функции при значени-
ях x, мало отличающихся от 1. Для этого составим таблицу значений функции в интересующем нас интервале (табл. 1.1).
Таблица 1.1
Мы видим, что чем ближе x приближается к 1, тем значения f (x) ближе к 2. В подобных случаях говорят, что число 2 является пределом функции f (x) при x, стремящимся к 1 (или более кратко: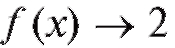 при
при
x - 1).
Дадим теперь строгое определение предела функции. Определение. Пусть функция f (x) определена в некоторой окрестности точки кроме, может быть, самой точки Число b называется пределом функции в точке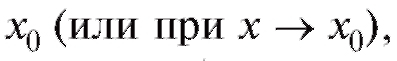 если для любого положительного
если для любого положительного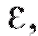 как бы мало оно не было, выполняется неравенство
как бы мало оно не было, выполняется неравенство 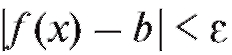 для всех
для всех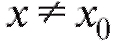 из некоторой окрестности точки Записывают так:
из некоторой окрестности точки Записывают так: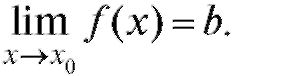
Геометрический смысл этого определения: для любой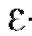 -окрестности точки b (рис. 1.22) существует некоторая окрестность точки
-окрестности точки b (рис. 1.22) существует некоторая окрестность точки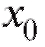 (например, δ-окрестность), такая что для всех
(например, δ-окрестность), такая что для всех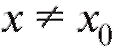 из этой окрестности соответствующие точки графика f (x) лежат внутри полосы шириной 2е, ограниченной прямыми y = b + е, y = b - е.
из этой окрестности соответствующие точки графика f (x) лежат внутри полосы шириной 2е, ограниченной прямыми y = b + е, y = b - е.
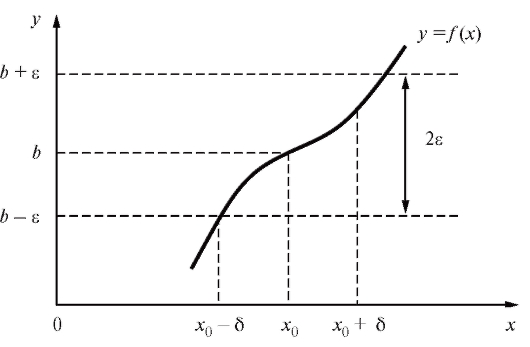
Рис. 1.22. Геометрический смысл предела функции в точке х0)
В данном определении не оговаривается способ приближения x к Х0: слева, справа или колеблясь около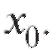 В некоторых случаях это существенно.
В некоторых случаях это существенно.
Определение. Число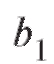 называется пределом функции y = f (x) слева в точке
называется пределом функции y = f (x) слева в точке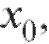 если
если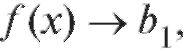 когда
когда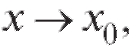 оставаясь меньше Х0.
оставаясь меньше Х0.
Записывается это так: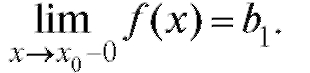
Аналогично определяется и записывается предел функции справа: 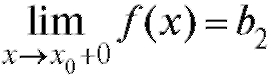 , если
, если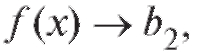 когда
когда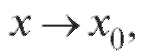 оставаясь больше Х0.
оставаясь больше Х0.
Пределы функции слева и справа называются односторонними (рис. 1.23). Очевидно, что если существует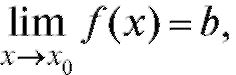 то оба односто-
то оба односто-
ронних предела также существуют и равны b.
Справедливо и обратное утверждение: если существуют односторонние пределы, оба равные b, то
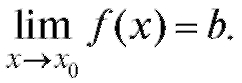
Если же односторонние пределы не равны между собой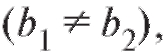 то
то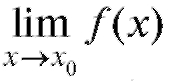 не существует.
не существует.
Если функция y = f (x) определена в промежутке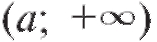 , то можно определить предел функции при
, то можно определить предел функции при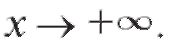
Определение. Число b называется пределом функции при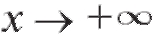 (т. е.
(т. е. 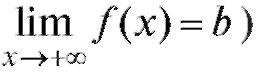 , если для лю-
, если для лю-
бого сколь угодно малогои всех достаточно больших x выполняется  неравенство
неравенство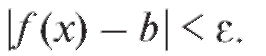
На рис. 1.24 значения функции f (x) при всех x > E попадают в е-окрестность точки b.
Аналогично определяется предел функции при
Если пределы функции f (x) при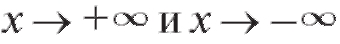 существуют и рав-
существуют и рав-
ны, скажем, A, то говорят, что f (x) имеет предел A при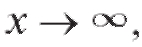 и пишут
и пишут
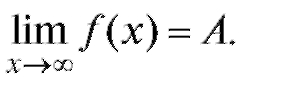
В данных ранее определениях пределов предполагалось, что они конечны. В случае, если функция f (x) неограниченно возрастает или убы-
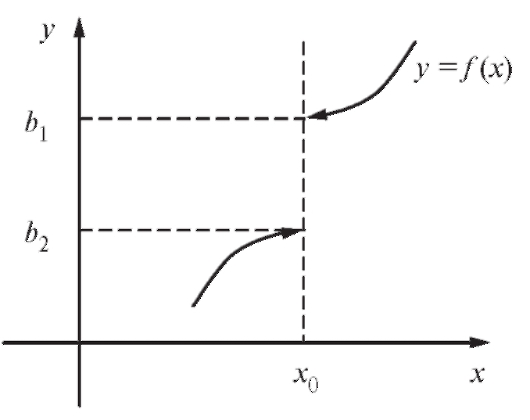
Рис. 1.23. Иллюстрация к определению односторонних пределов
вает при x - Х0, говорят, что предел f (x) равен бесконечности
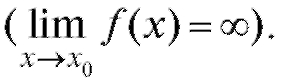
Среди функций, имеющих пределы (в точке или на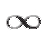 ), выделяют класс функций, имеющих предел, равный 0. Такие функции называются бесконечно малыми функциями (бесконечно малыми величинами) и обозначаются буквами
), выделяют класс функций, имеющих предел, равный 0. Такие функции называются бесконечно малыми функциями (бесконечно малыми величинами) и обозначаются буквами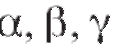 и т. д.
и т. д.
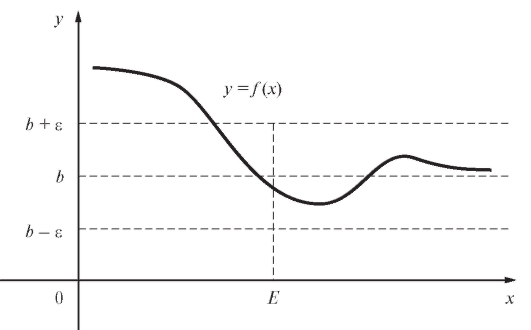
Рис. 1.24. Предел функции при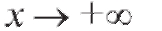
При вычислении пределов часто используется понятие эквивалентности бесконечно малых величин.
Определение. Пусть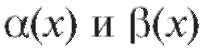 - бесконечно малые функции. Если
- бесконечно малые функции. Если
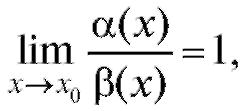 то
то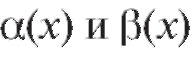 называются эквивалентными
называются эквивалентными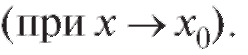
1.2.2. Основные теоремы о пределах
Этот пункт посвящен основным свойствам пределов функций, которые позволяют вычислять пределы функций, определяемых алгебраическими действиями над переменной. В приводимых далее теоремах предполагается, что функции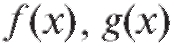 имеют общую область определения, содержащую точку Х0, и обладают конечными пределами в этой точке. Теорема 1.1. Предел суммы двух функций равен сумме их пределов.
имеют общую область определения, содержащую точку Х0, и обладают конечными пределами в этой точке. Теорема 1.1. Предел суммы двух функций равен сумме их пределов.
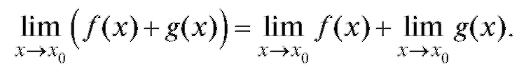
Теорема 1.2. Предел произведения двух функций равен произведению их пределов.
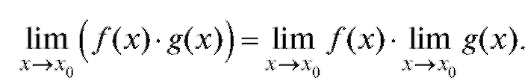
Следствие. Постоянный множитель можно выносить за знак предела.
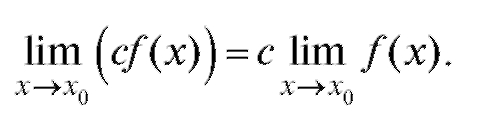
Теорема 1.3. Предел отношения двух функций равен отношению пределов этих функций, если предел знаменателя отличен от 0.
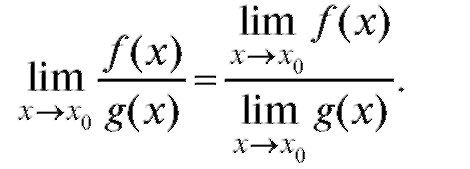
Теорема 1.4. Предел положительной функции не отрицателен. Эти утверждения справедливы и при x, стремящемся к.
1.2.3. Специальные пределы
Если в случае применения основных теорем о пределах функции возникают выражения вида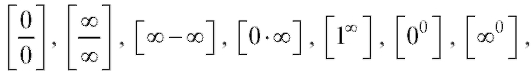
которые носят название неопределенностей, то для получения ответа (так называемые раскрытия неопределенности) применяются специальные методы.
Для решения примеров используются следующие пределы:
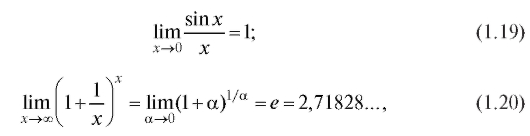
которые называются первым и вторым замечательными пределами соответственно.
Напоминаем (см. п. 1.1.4), что число e является основанием натурального логарифма.
При вычислении пределов полезно также иметь в виду следующие равенства, вытекающие из (1.19) и (1.20):
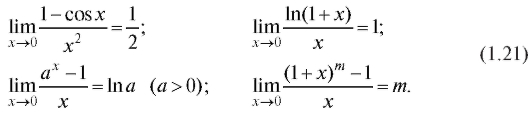
1.2.4. Примеры нахождения некоторых пределов
Пример 1. Найти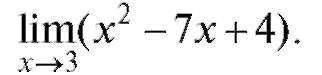
Решение. Применяя теоремы о пределах (теорема 1.1) и заменяя в аналитическом выражении x его предельным значением, получаем
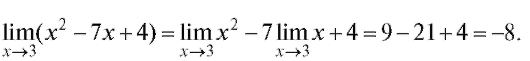
Пример 2. Найти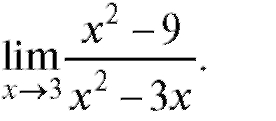
Решение. Числитель и знаменатель дроби стремятся к нулю при x, стремящемся к 3 (принято говорить, что получается неопределенность
вида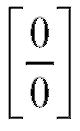 ). Имеем
). Имеем
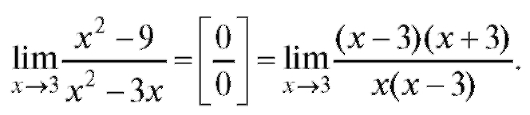
Так как в определении предела функции отмечено, что при отыскании предела функции значения функции в предельной точке можно не рассматривать, то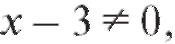 вследствие чего можно разделить числитель
вследствие чего можно разделить числитель
на знаменатель и получить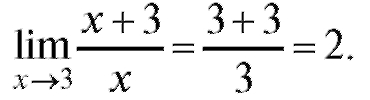
Пример 3. Найти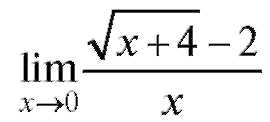 (неопределенность
(неопределенность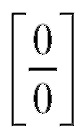 ).
).
Решение. Умножим числитель и знаменатель дроби на сумму
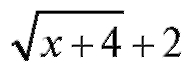 (сопряженное выражение). Воспользуемся известной формулой алгебры
(сопряженное выражение). Воспользуемся известной формулой алгебры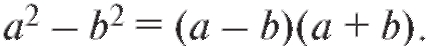 Получим
Получим
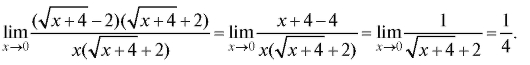
Пример 4. Найти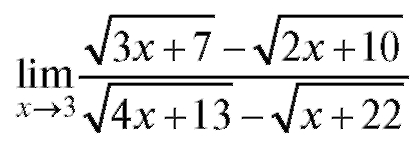 (неопределенность
(неопределенность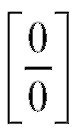 ).
).
Решение. Числитель и знаменатель дроби нужно одновременно умножить на их сопряженные выражения, т. е. на выражение
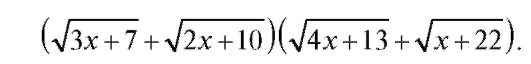
Получаем
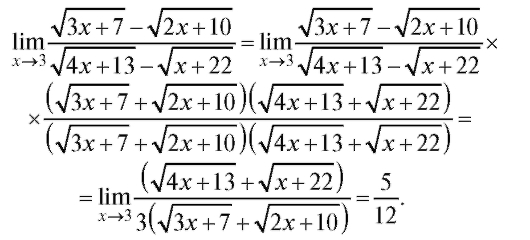
Пример 5. Найти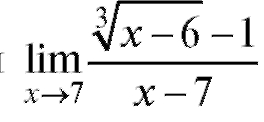 (неопределенность
(неопределенность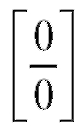 ).
).
Решение. Воспользуемся известной алгебраической формулой
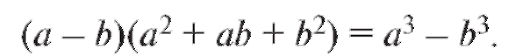
Положим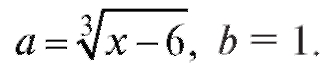 Значит, чтобы получить в числителе раз-
Значит, чтобы получить в числителе раз-
ность кубов, надо его умножить на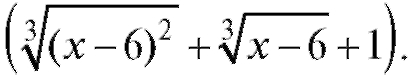 Умножая чис-
Умножая чис-
литель и знаменатель на эту величину, получаем
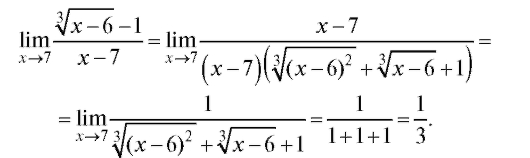
Пример 6. Найти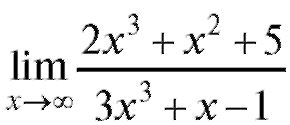 (неопределенность
(неопределенность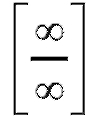 ).
).
Решение. Разделим и числитель, и знаменатель на высшую степень x, встречающуюся в членах дроби, а после этого перейдем к пределу:
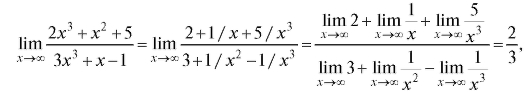
так как при величины
величины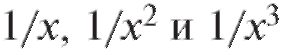 являются бесконечно ма-
являются бесконечно ма-
лыми, т. е. пределы этих величин равны нулю, когда Теперь воз-
Теперь воз-
можно применить теорему о пределе частного.
Пример 7. Найти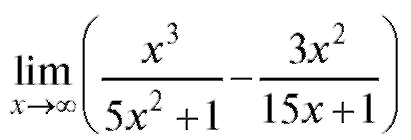 (неопределенность
(неопределенность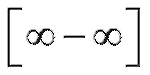 ).
).
Решение. Приведем выражение к общему знаменателю, а затем разделим числитель и знаменатель на высшую степень x, встречающуюся в дроби.
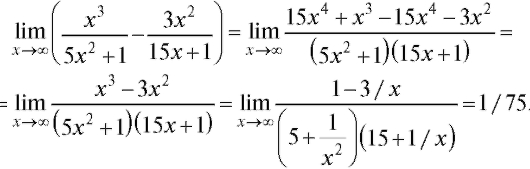
Пример 8. Найти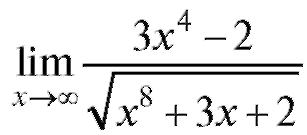 (неопределенность
(неопределенность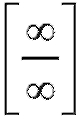 ).
).
Решение. Разделим числитель и знаменатель на высшую степень x, встречающуюся в примере, т. е. на х4.
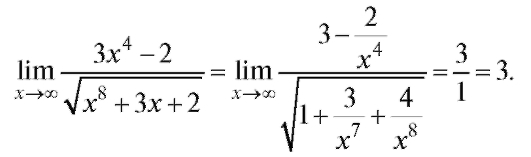
Пример 9. Найти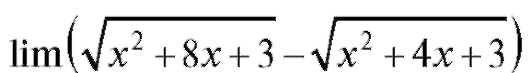 (неопределенность
(неопределенность
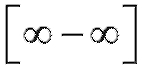 ).
).
Решение. Умножим и разделим рассматриваемое выражение на сопряженное:
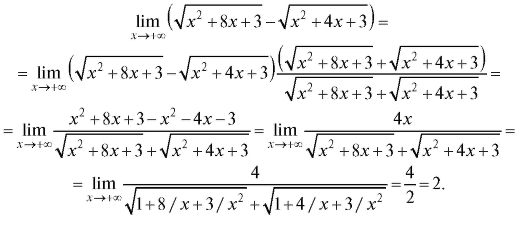
Пример 10. Найти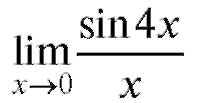 (неопределенность
(неопределенность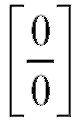 ).
).
Решение. Используем первый замечательный предел:
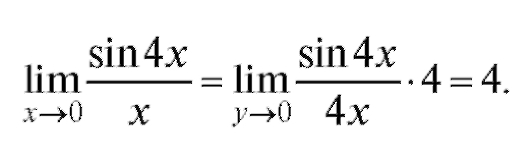
Пример 11. Найти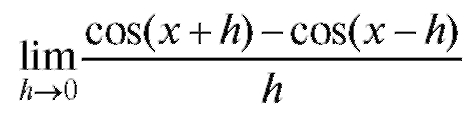 (неопределенность
(неопределенность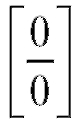 ).
).
Решение. Применяя формулу
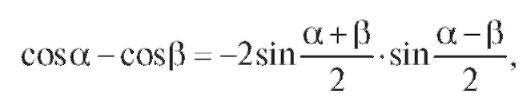
получим
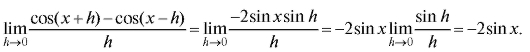
Пример 12. Найти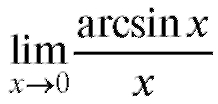 (неопределенность
(неопределенность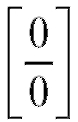 ).
).
Решение. Заменим arcsin x на y; если x → 0, то arcsin x→ 0, y→ 0 и arcsin x = y, отсюда sin y = x.
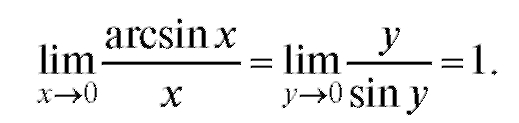
Пример 13. Найти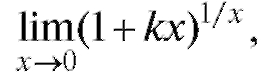 где к - любое число, не равное
где к - любое число, не равное
нулю.
Решение. Произведем замену переменной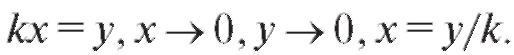
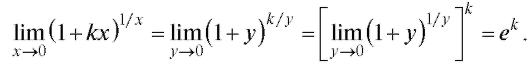
Аналогично можно доказать равенство: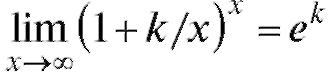 .
.
Пример 14. Найти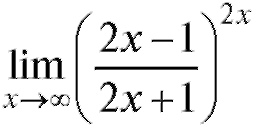 (неопределенность
(неопределенность ).
).
Решение.
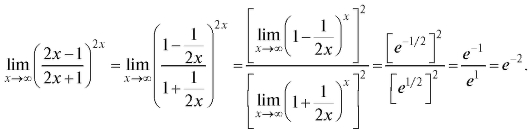
Пример 15. Найти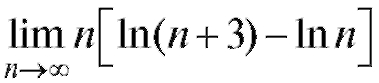 (неопределенность
(неопределенность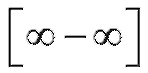 ).
).
Решение.
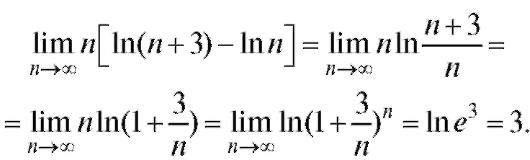
Пример 16. Найти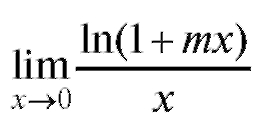 (неопределенность
(неопределенность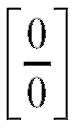 ).
).
Решение.
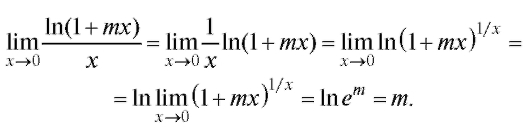
Пример 17. Найти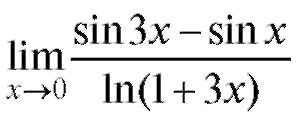 (неопределенность
(неопределенность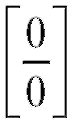 ).
).
Решение.
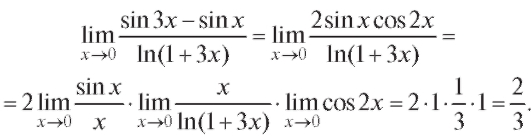
Пример 18. Найти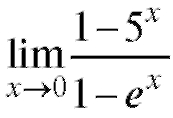 (неопределенность
(неопределенность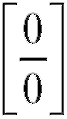 ).
).
Решение.
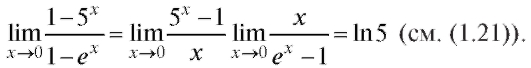
Пример 19. Найти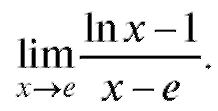
Решение. Произведем замену переменной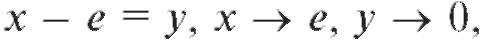 x = y + е. Получим (см. (1.21)):
x = y + е. Получим (см. (1.21)):
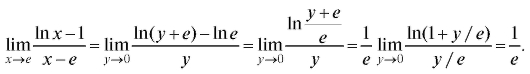
Самостоятельная работа
Найти пределы (1-50).
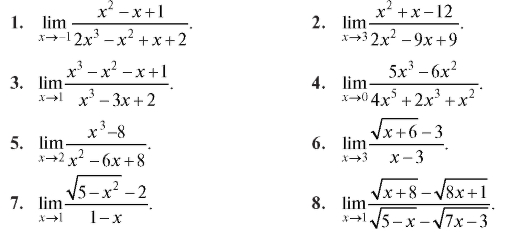

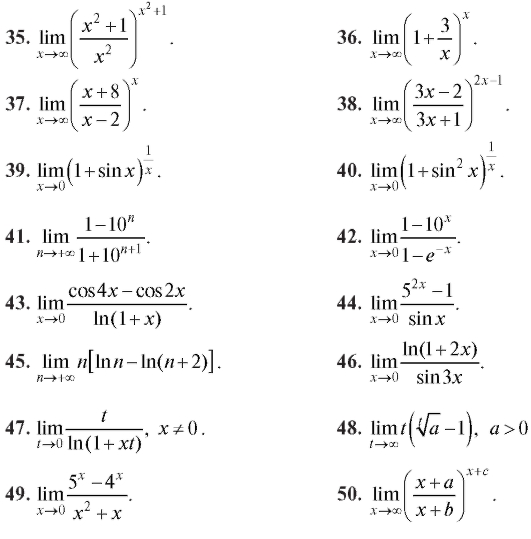
1.3. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ 1.3.1. Основные понятия и определения
Рассмотрим функцию y = f (x), определенную в интервале [a; b]. Пусть x0 и x - два произвольных значения из этого интервала. Обозначим Говорят, что для перехода от значения аргумента x0 к значению x первоначальному значению придано приращение
Говорят, что для перехода от значения аргумента x0 к значению x первоначальному значению придано приращение Приращением
Приращением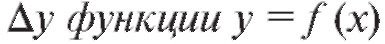 , соответствующим приращению
, соответствующим приращению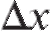 аргумента x в точке х0, называется разность
аргумента x в точке х0, называется разность
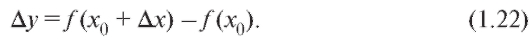
Пример. Найти приращение функции y = x2, соответствующее приращению Дх аргумента x в точке Решение. По формуле (1.22)
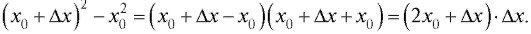
С понятием предела функции тесно связано еще одно понятие математического анализа - понятие непрерывности функции.
Определение. Говорят, что функция f (x) непрерывна в точке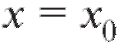 , если
, если

Отметим, что (1.23) равносильно соотношению

т. е. функция f (x) непрерывна в точке х0, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. При этом предполагается, что бесконечно малая величина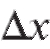 пробегает лишь те значения, для которых
пробегает лишь те значения, для которых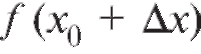 имеет смысл.
имеет смысл.
Определение. Функция f (x) называется непрерывной в интервале, если эта функция непрерывна в каждой точке этого интервала.
Для функции, непрерывной в интервале (а; b), для каждого значения 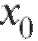 из интервала (а; b) выполнено равенство (1.23). Так как
из интервала (а; b) выполнено равенство (1.23). Так как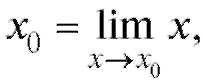 то
то
отсюда получим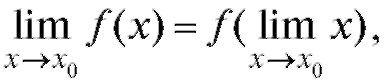 т. е. если функция непрерывна, то
т. е. если функция непрерывна, то
знаки предела и функции можно менять местами.
1.3.2. Основные теоремы непрерывности
Теорема 1.5. Если две функции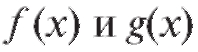 определены в одном и том
определены в одном и том
же промежутке и обе непрерывны в точке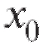 из этого промежутка, то в той же точке будут непрерывны и функции
из этого промежутка, то в той же точке будут непрерывны и функции
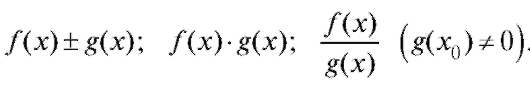
Этот факт непосредственно вытекает из теорем 1.1-1.3 из п. 1.2.2 о пределе суммы, разности, произведения и частного двух функций.
Теорема 1.6. Все основные элементарные функции непрерывны там, где они определены.
Теорема 1.7. Пусть сложная функция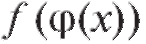 определена на множе-
определена на множе-
стве X (см. п. 1.1.3). Если функция ,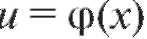 непрерывна в точке
непрерывна в точке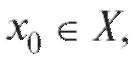 а
а
f (u) непрерывна в соответствующей точке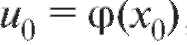 , то сложная функ-
, то сложная функ-
ция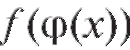 будет непрерывна в точке х0.
будет непрерывна в точке х0.
1.3.3. Точки разрыва функции
Определение. Если функция f (x) не является непрерывной в точке то говорят, что в точке Х0 функция f (x) разрывна, а точка Х0 называется точкой разрыва функции.
Можно показать, что функция f (x) разрывна в точке если нарушается одно из нижеследующих 4-х условий непрерывности.
1. Функция f (x) должна быть определена в некоторой окрестности точки х0.
2. Должны существовать конечные пределы слева и справа
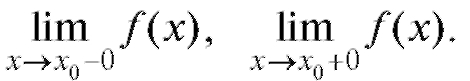
3. Эти пределы слева и справа должны быть равны
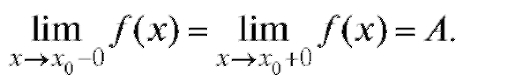
4. Эти пределы должны быть равны значению функции в точке х0, т. е.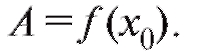
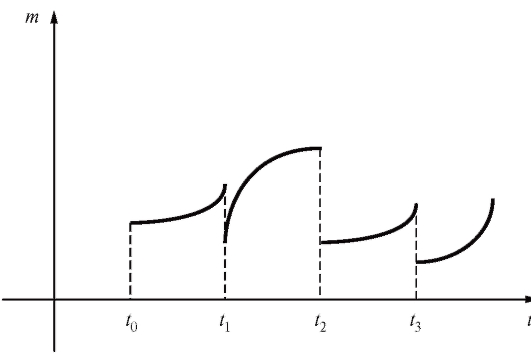
Рис. 1.25. Зависимость биомассы микроорганизмов от температуры
В качестве конкретного примера функции, имеющей точку разрыва, рассмотрим изменение биомассы микроорганизмов, чувствительных к температурным колебаниям.
При изменении температуры общая биомасса m, как правило, увеличивается - тепло способствует размножению. Однако когда температура слишком высока, практически все колонии гибнут; значение
m, скачкообразно меняясь, становится равным нулю. Примерно то же самое происходит и при понижении температуры: как только она достигнет некоторого нижнего предела, микроорганизмы погибают. В реальных условиях температура меняется в зависимости от времени, то повышаясь, то понижаясь. Поэтому графическим изображением изменения биомассы в зависимости от времени может быть разрывная кривая. Точки разрыва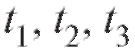 соответствуют тем моментам времени, когда температура стала слишком высокой или слишком низкой (рис. 1.25).
соответствуют тем моментам времени, когда температура стала слишком высокой или слишком низкой (рис. 1.25).
1.3.4. Классификация точек разрыва
Пусть х0 является внутренней точкой отрезка [а; b].
Если существуют конечные пределы f (x) при стремлении x к x0 слева и справа, но нарушены условия 3 или 4, то точку х0 называют точкой разрыва первого рода.
Если хотя бы один из пределов слева или справа бесконечен или не существует, тогда говорят о разрыве второго рода.
Легко понять, при каких обстоятельствах для функции f (x) в точке а справа появляется разрыв. Может случиться, что хотя конечный предел f (a + 0) и существует, но он не равен значению f (a). Аналогично, в точке b появляется разрыв, если существует конечный предел f (b - 0), но он не равен f (b).
Если существуют конечные пределы функции f (x) при стремлении x к x0 слева и справа, они равны между собой, но не равны значению функции в этой точке, то восстановить непрерывность в точке х0 можно, положив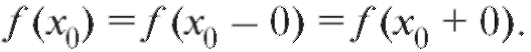 В этом случае точка х0 называется
В этом случае точка х0 называется
устранимой точкой разрыва.
Если функция f (x) в точке х0 имеет разрыв второго рода, в этом случае, как бы дополнительно не определять функцию при x = х0, она неизбежно будет иметь разрыв.
Пример 1. Указать точку разрыва функции 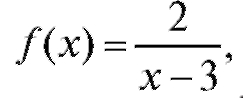 найти
найти
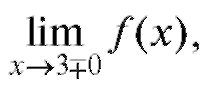 определить, какого рода разрыв терпит функция в этой точке. Решение.
определить, какого рода разрыв терпит функция в этой точке. Решение.
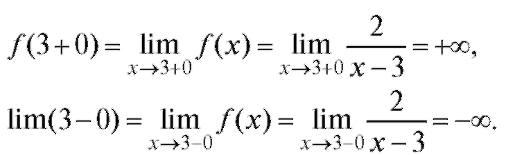
В точке x = 3 разрыв второго рода.
Пример 2. Построить график функции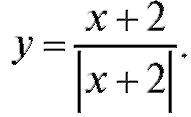 Какие из условий
Какие из условий
непрерывности в точках разрыва выполнены и какие не выполнены?
Решение. График функции представлен на рис. 1.26.
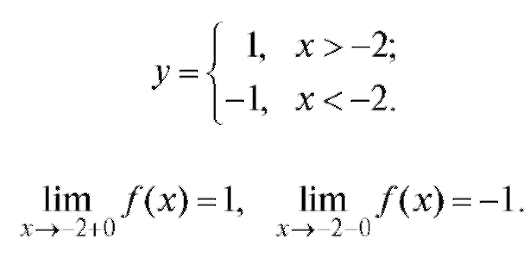
Конечные пределы слева и справа существуют, но не равны между собой. В точке x = -2 разрыв первого рода.
Пример 3. Построить график функции
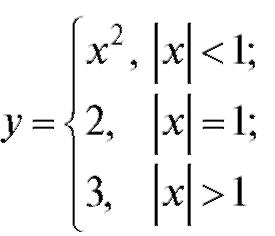
и указать точки ее разрыва.
Решение. График функции приведен на рис. 1.27.
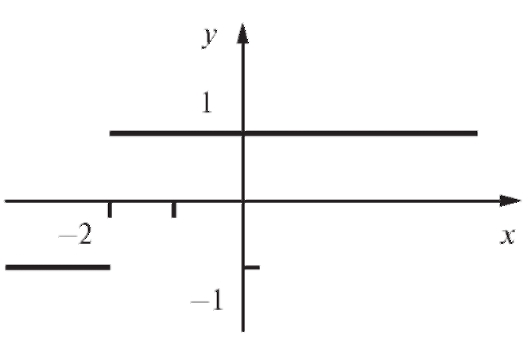
Рис. 1.26. График функции к примеру 2
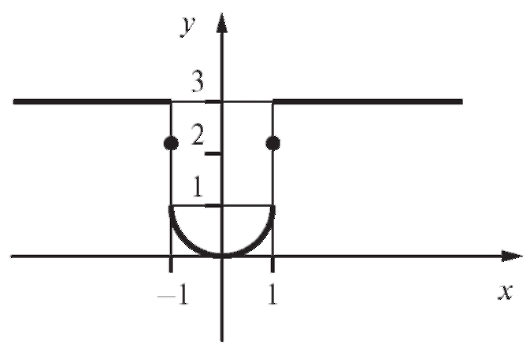
Рис. 1.27. График функции к примеру 3
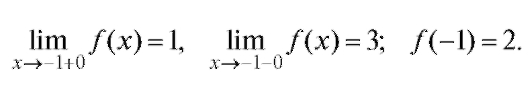
Пределы слева и справа конечны, но не равны между собой. И не равны значению функции в этой точке. В точке x = -1 разрыв первого рода.
Аналогично, в точке x = 1 разрыв первого рода.
Пример 4. Найти точку разрыва и построить график функции
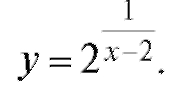
Решение.
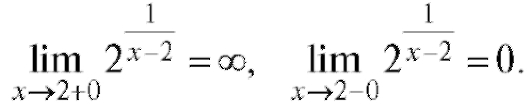
В точке x = 2 разрыв второго рода. График функции приведен на рис. 1.28. Пример 5. Пусть
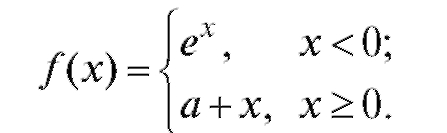
При каком выборе числа а функция будет непрерывной? Решение.
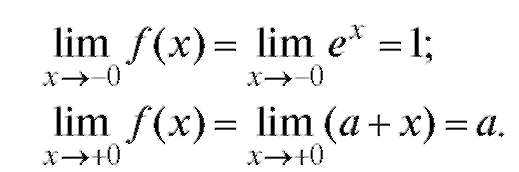
Функция будет непрерывна при а = 1
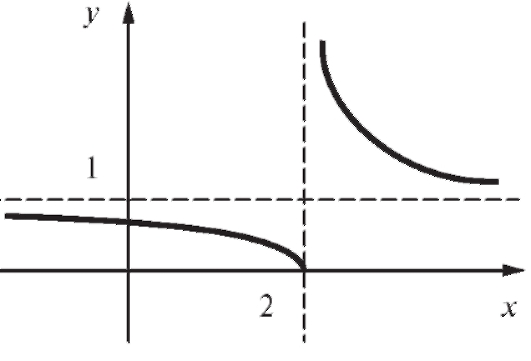
Рис. 1.28. График функции к примеру 4
Самостоятельная работа
1. Пусть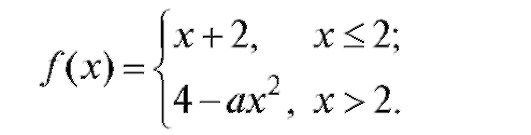
При каком выборе числа а функция будет непрерывной? (Построить ее график.)
2. Исследовать характер разрыва функции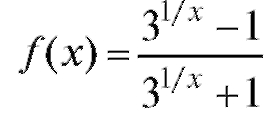 в точке x = 0.
в точке x = 0.
3. Исследовать непрерывность функции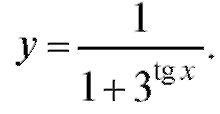
4. Исследовать характер разрыва функции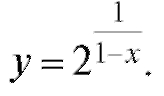
5. Исследовать непрерывность и построить график функции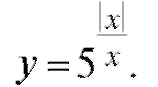
6. Найти точку разрыва функции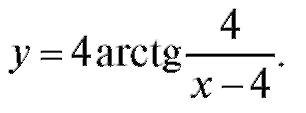
7. Исследовать на непрерывность функцию и изобразить графически
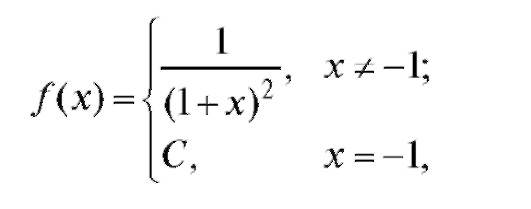
где С - произвольная постоянная.
8. Исследовать на непрерывность
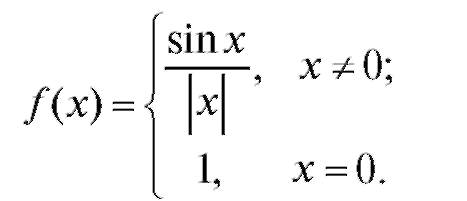

11. Исследовать на непрерывность и построить график функции
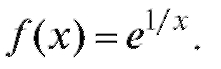
12. Исследовать на непрерывность и построить график функции
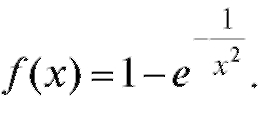
13. Является ли непрерывной функция