Математика : учебник / И. В. Павлушков, Л. В. Розовский, И. А. Наркевич. - 2013. - 320 c. : ил.
|
|
|
|
Глава 9. ВВЕДЕНИЕ В ТЕОРИЮ МАССОВОГО ОБСЛУЖИВАНИЯ. ФОРМУЛЫ ЭРЛАНГА
С работой своеобразных систем, называемых системами массового обслуживания (СМО), приходится сталкиваться повседневно. Примерами таких СМО могут служить телефонные станции, ремонтные службы, билетные кассы, справочные бюро, магазины, аптеки, парикмахерские, т. е. любые системы, предназначенные для обслуживания (в том или ином смысле) некоторого потока заявок (или «требований»), поступающих в какие-то, вообще говоря, случайные моменты времени.
Каждая СМО состоит из некоторого числа обслуживающих единиц (или «приборов»), называемых каналами обслуживания. Каналами могут быть линии связи, лифты, продавцы, кассиры и т. д.
Время обслуживания потока заявки длится какой-то, как правило, случайный, промежуток времени, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времен обслуживания приводит к тому, что в какие-то периоды времени на входе СМО создается очередь, в другие же периоды СМО будет работать с недогрузкой.
Таким образом, процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем: состояние СМО меняется скачком в моменты появления прихода новой заявки или окончания обслуживания (клиент пришел - клиент ушел).
Предметом теории массового обслуживания (ТМО) является построение математических моделей, связывающих данные условия работы СМО (характер потока заявок, число каналов и их производительность, дисциплина обслуживания) с показателями эффективности СМО.
В качестве таких показателей могут использоваться разные характеристики: среднее число заявок, обслуживаемых в единицу времени; среднее число занятых каналов; вероятность отказа в обслуживании.
Рассмотрим следующий пример.
Пусть речь идет об аптеке, в которой работает несколько служащих (каналов обслуживания). Клиенты, обратившиеся за медикаментами, образуют поток требований. Представьте, что в аптеку забежал покупатель, готовый приобрести дорогое лекарство, но не располагающий
временем или желанием стоять в очереди. Надо уметь вычислять вероятность того, что он не будет обслужен - ведь если большинство клиентов уйдет без покупки, вряд ли стоит держать аптеку вообще. Полезно также знать степень загрузки каждого работника, это характеризует рентабельность аптеки. Поскольку число потенциальных клиентов и время обслуживания величины случайные, задача решается далеко не просто.
В примере условие ухода клиента, если его обслуживание не началось немедленно, выглядит несколько искусственным - большинство покупателей могут подождать. Однако если вместо аптеки рассматривать АТС (автоматическую телефонную станцию), а обслуживанием считать продолжительность телефонного разговора, то вышеупомянутое условие выполняется.
Если абстрагироваться от реального наполнения моделей СМО (мастерская, аптека, АТС, лифты в доме и т. д.), СМО можно описать, задавая следующие ее составляющие (рис. 9.1):
1. Входящий поток требований.
2. Дисциплину очереди.
3. Механизм обслуживания.
4. Выходящий поток требований.
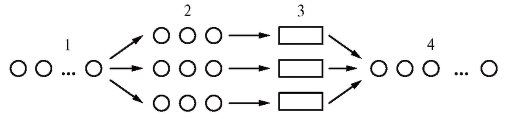
Рис. 9.1. Модель теории массового обслуживания
В некоторых системах «очередь» отсутствует.
СМО делится на классы по ряду признаков, например СМО с отказами (как в телефонии) и СМО с очередью. На практике чаще встречаются и имеют большее значение СМО с очередью: недаром ТМО иногда называют «теория очередей». В СМО с очередью длина очереди и (или) время ожидания могут быть ограничены или не иметь ограничений; обслуживание может быть с приоритетом или без него, в порядке поступления или случайным.
Приоритет может быть абсолютным или относительным.
СМО могут быть открытыми и закрытыми. В первой - поток заявок не зависит от состояния самой СМО (сколько каналов занято), во
второй - зависит. Пример - наладка группы станков одним рабочим. Здесь интенсивность «требований» со стороны станков зависит от того, сколько их уже неисправно.
Классификация СМО не ограничивается приведенными разновидностями.
Возвращаясь к компонентам СМО, рассмотрим более подробно входящий поток требований, как одно из наиболее важных понятий ТМО.
Потоком требований называется совокупность заявок на обслуживание, поступающих в обслуживающую систему. Он может быть регулярным или стохастическим (т. е. случайным). В первом случае требования следуют друг за другом через равные промежутки времени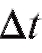 , во втором случае моменты появления требований - случайные величины.
, во втором случае моменты появления требований - случайные величины.
Важной характеристикой потока требований является его интенсивность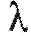 - среднее число требований, поступающих в систему в единицу времени. Для регулярного потока
- среднее число требований, поступающих в систему в единицу времени. Для регулярного потока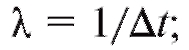 в общем случае интенсив-
в общем случае интенсив-
ность может быть как постоянной, так и зависящей от t. Например, поток машин ночью не так интенсивен, как днем.
Входящий поток называется стационарным, если вероятность поступления определенного количества требований в течение определенного промежутка времени зависит лишь от длины этого промежутка.
В частности интенсивность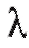 стационарного потока должна быть постоянной, т. е. в среднем на интервалах равной длины должно быть одинаковое количество требований.
стационарного потока должна быть постоянной, т. е. в среднем на интервалах равной длины должно быть одинаковое количество требований.
Свойством стационарности обладают многие реальные потоки требований, по крайней мере, на ограниченном участке времени (нагрузка на АТС меняется в течение суток, но не между, скажем, часом и двумя).
Поток требований называется потоком без последействия, если для любых двух непересекающихся участков времени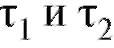 число требова-
число требова-
ний, поступивших в систему за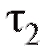 , не зависит от того, сколько требований поступило за промежуток
, не зависит от того, сколько требований поступило за промежуток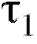 .
.
Другими словами, прошлое не влияет на настоящее! По сути, это означает, что требования, образующие поток, появляются в те или иные моменты времени независимо друг от друга (как, например, поток пассажиров, входящих в метро).
Пусть случайная величина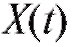 обозначает число требований на интервале [0; t].
обозначает число требований на интервале [0; t].
Поток называется ординарным, если
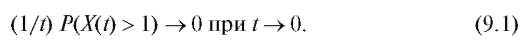
Заметим, что
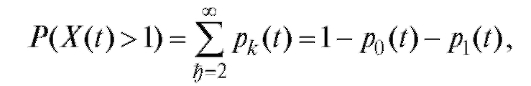
где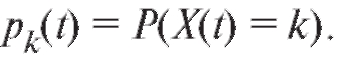
В ординарном потоке появление двух и более требований за малый промежуток времени практически невозможно. Поток клиентов в аптеку обычно ординарен.
Поток требований называется простейшим, если он стационарен, ординарен и не имеет последействия. Потоки такого типа часто встречаются на практике. Термин «простейший» связан с простым математическим описанием этих потоков.
Можно показать, что для простейшего потока число требований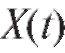 в промежутке времени длиной t распределено по закону Пуассона с параметром
в промежутке времени длиной t распределено по закону Пуассона с параметром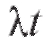 (см. п. 7.2.1), т. е.
(см. п. 7.2.1), т. е.
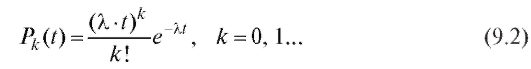
Стационарность и отсутствие последействия налицо, ординарность (т. е. условие (9.1)) вытекает из равенства
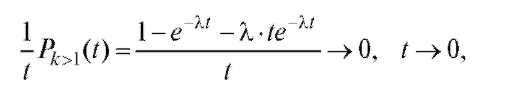
которое можно проверить по правилу Лопиталя.
Параметр X здесь характеризует интенсивность потока. Действительно,
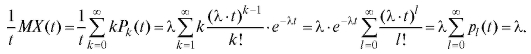
Простейший поток еще называют стационарным пуассоновским.
Пример 1. Рассмотрим наладку станков одним рабочим. Предполагается, что все станки находятся приблизительно в одинаковом состоянии (последнее обеспечивает стационарность потока поломок). Вероятность поломки одного станка невелика (двух, трех и т. д. - тем более) - отсюда следует ординарность. Кроме того, если станков много, а среднее время ремонта мало, то можно считать, что поток поломок не имеет последействия. Другими словами, он является простейшим.
Решение. Пусть интенсивность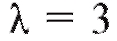 поломки/ч. По формуле (9.2)
поломки/ч. По формуле (9.2)
при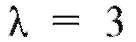 и t =1 найдем вероятность k поломок в течение часа
и t =1 найдем вероятность k поломок в течение часа
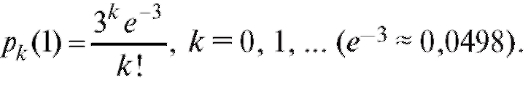 Составим табл. 9.1. Таблица 9.1
Составим табл. 9.1. Таблица 9.1
Следующее важное понятие ТМО - это время обслуживания.
Оно является характеристикой функционирования каждого отдельного канала обслуживающей системы и отражает его пропускную способность. Время обслуживания - случайная величина.
Для простоты будем рассматривать систему, состоящую из однотипных обслуживающих аппаратов, имеющих общий закон распределения. При этом будем предполагать, что этот закон распределения - показательный, с функцией распределения времени обслуживания (см. формулу (7.19))
Параметр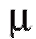 (аналогично параметру
(аналогично параметру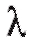 входящего потока) определяет интенсивность обслуживания; величина является средним временем обслуживания t одной заявки:
входящего потока) определяет интенсивность обслуживания; величина является средним временем обслуживания t одной заявки: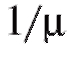

Показательный закон имеет большое значение как в теоретических исследованиях, так и во многих приложениях. Важнейшим его свойством является то, что при таком законе распределения времени обслуживания оставшееся время обслуживания не зависит от того, сколько времени обслуживание уже длилось.
Далее коротко опишем я-канальную систему массового обслуживания с отказами. Это «классическая» задача ТМО, возникшая из практических нужд телефонии и решенная в начале ХХ века датским математиком Эрлангом. Задача ставится так.
Имеется я каналов, на которые поступает простейший поток заявок с интенсивностью X. Если в момент поступления очередного требования имеется хотя бы один свободный аппарат, то любой из аппаратов немед-
ленно приступает к обслуживанию. В противном случае заявка получает отказ и покидает систему.
Все каналы работают независимо друг от друга и от входящего потока.
Время обслуживания каждого требования распределено по показательному закону (см. (9.3)) с параметром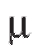 (т. е. среднее время обслуживания
(т. е. среднее время обслуживания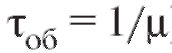 ). Требуется найти характеристики эффективности работы СМО в стационарном (установившемся) режиме, т. е. при неограниченно возрастающем времени ее работы. Конкретнее нас интересуют:
). Требуется найти характеристики эффективности работы СМО в стационарном (установившемся) режиме, т. е. при неограниченно возрастающем времени ее работы. Конкретнее нас интересуют:
• А - абсолютная пропускная способность, т. е. среднее число заявок, обслуживаемых в единицу времени;
• относительная пропускная способность, или средняя доля пришедших заявок, обслуживаемых системой;
• Ротк - вероятность отказа, или того, что заявка покинет СМО необслуженной;
• 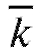 - среднее число занятых каналов;
- среднее число занятых каналов;
• 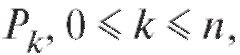 - вероятность того, что занято ровно k каналов, и, в частности, Р0 - вероятность простоя системы;
- вероятность того, что занято ровно k каналов, и, в частности, Р0 - вероятность простоя системы;
• 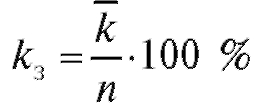 - коэффициент занятости каналов в процентах (%);
- коэффициент занятости каналов в процентах (%);
• 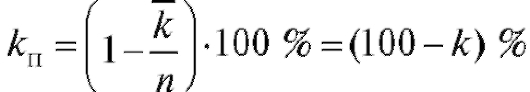 - коэффициент простоя каналов
- коэффициент простоя каналов
в процентах (%). Обозначим

Величина а обычно называется «приведенной интенсивностью потока заявок» и ее смысл - среднее число заявок, приходящее за среднее время обслуживания одной заявки. Пользуясь этим обозначением, можно показать, что вероятность Р0 того, что все я каналов СМО свободны, выражается формулой:
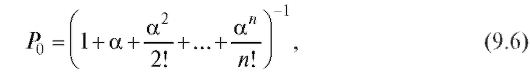
а вероятности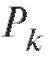 при
при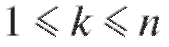 имеют вид
имеют вид

Формулы (9.6), (9.7) для вероятностей Рк называются формулами Эрланга - в честь основателя ТМО. С их помощью можно вычислить остальные интересующие нас характеристики СМО. Так, вероятность 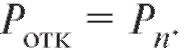 Действительно, для того чтобы пришедшая заявка получила отказ, необходимо, чтобы все я каналов были заняты. Итак,
Действительно, для того чтобы пришедшая заявка получила отказ, необходимо, чтобы все я каналов были заняты. Итак,

Отсюда находим относительную пропускную способность, т. е. вероятность, что заявка будет обслужена:
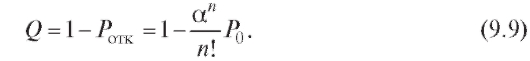
Абсолютную пропускную способность получим, умножая интенсивность потока заявок на Q:
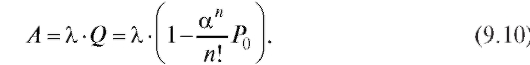
Среднее число занятых каналов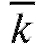 по определению математического ожидания с учетом формул (9.6) и (9.7) равно
по определению математического ожидания с учетом формул (9.6) и (9.7) равно
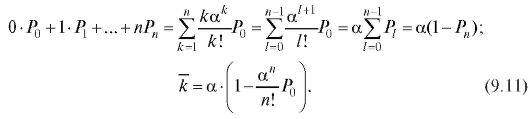
Отметим, что, зная вероятность отказа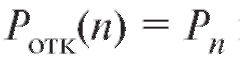 в обслуживании
в обслуживании
системы с я каналами обслуживания (см. (9.8)), аналогичную вероятность для системы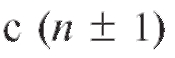 каналом можно вычислить, пользуясь несложно проверяемыми равенствами
каналом можно вычислить, пользуясь несложно проверяемыми равенствами
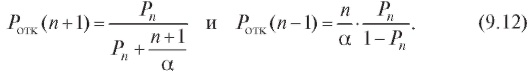
Приведем два примера, использующих рассмотренную теорию. Пример 2. Пусть имеется АТС с пятью линиями связи. Поток вызовов, поступающий на АТС, предполагается простейшим с интенсивностью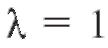 вызова в минуту, а время разговора - распределенным по показательному закону со средним временем разговора
вызова в минуту, а время разговора - распределенным по показательному закону со средним временем разговора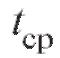 = 2 мин. Предполагается также, что требование получает отказ, если в момент его поступления все 5 линий заняты. Требуется вычислить основные характеристики эффективности СМО в установившемся режиме.
= 2 мин. Предполагается также, что требование получает отказ, если в момент его поступления все 5 линий заняты. Требуется вычислить основные характеристики эффективности СМО в установившемся режиме.
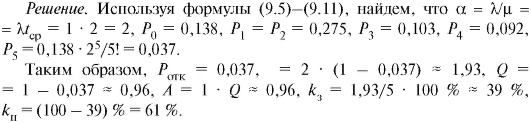
Отсюда заключаем, что на АТС в среднем занято 2 линии из 5, каждая линия загружена всего на 39 %, теряется приблизительно 4 вызова из 100. Таким образом, АТС работает не слишком эффективно, и вполне можно сократить общее число линий и (или) увеличить интенсивность потока заявок.
Пример 3. Следующий пример возвращает нас к задаче об эффективности работы аптеки. Пусть имеется аптека с обслуживающим персоналом из 3 человек. Статистическое обследование показало, что среднее число клиентов, обращающихся в аптеку в течение часа, равно 24, а среднее время обслуживания каждого клиента занимает 5 мин. Выясним, какова вероятность, что вас не обслужат (предполагается, что если все окошки заняты, то клиент уходит) и насколько продавцы загружены работой.
Решение. Будем предполагать, что клиенты образуют простейший поток (если аптека расположена на бойком месте, это можно эвристически обосновать), и воспользуемся формулами Эрланга для решения.

Казалось бы, одного продавца можно и даже нужно сократить. Проведенные расчеты, однако, этого не подтверждают. Действительно, пользуясь формулой (9.12), найдем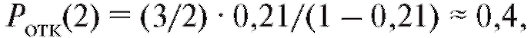
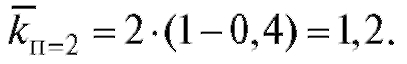 Таким образом, загрузка каждого из двух оставшихся продавцов немного вырастет (с 0,53 до 1/2 • 1,2 = 0,6 рабочего дня), зато «коэффициент полезного действия» аптеки упадет с 0,79 до 0,6, поскольку в сложившейся ситуации будет обслужено лишь 60 % ((1 - 0,4) • 100 %) потенциальных клиентов, а не 79 % как ранее при трех продавцах.
Таким образом, загрузка каждого из двух оставшихся продавцов немного вырастет (с 0,53 до 1/2 • 1,2 = 0,6 рабочего дня), зато «коэффициент полезного действия» аптеки упадет с 0,79 до 0,6, поскольку в сложившейся ситуации будет обслужено лишь 60 % ((1 - 0,4) • 100 %) потенциальных клиентов, а не 79 % как ранее при трех продавцах.