Глава 8. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Математической статистикой называют раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. Статистические данные здесь понимаются как сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми или иными признаками.

В первом приближении можно сказать, что главная цель математической статистики - получение осмысленных, научно обоснованных выводов из подверженных случайному разбросу данных. При этом само изучаемое явление, генерирующее эти данные, чаще всего слишком сложно, чтобы можно было составить его полное описание, отражающее все детали. Поэтому статистические выводы делаются на основе некоторой математической вероятностной модели реального случайного явления, которая должна воспроизводить его существенные черты и исключать те, которые предполагаются несущественными. Методы математической статистики позволяют по наблюдениям над изучаемым явлением определить вероятностные характеристики случайных величин, участвующих в математической модели, описывающей это явление.

Применительно к предстоящему изложению мы, в первую очередь, будем интересоваться задачами точечного и интервального оценивания параметров распределений исследуемых случайных величин, а также задачами статистической проверки гипотез относительно этих параметров.

8.1. ВЫБОРОЧНЫЙ МЕТОД 8.1.1. Генеральная совокупность. Выборка

Всякое каким-то образом выделенное множество объектов, которые могут отличаться друг от друга значением некоторой определенной характеристики, называется генеральной совокупностью.

Число элементов генеральной совокупности называется ее объемом.

Часть генеральной совокупности, случайным образом отобранная для наблюдений, называется случайной выборкой или, для краткости, выборкой.

Число элементов выборки называется ее объемом.

Так, если из ста тысяч упаковок некоторого лекарства (генеральная совокупность) для контроля качества отобрано сто упаковок (выборка), то объем генеральной совокупности составляет 100 000, а объем выборки - 100.

Поскольку мы рассчитываем с помощью статистических методов высказать определенное суждение о свойствах генеральной совокупности по свойствам выборки, последняя должна быть репрезентативной (представительной), т. е. должна быть организована таким образом, чтобы, по возможности, отражать все интересующие нас свойства генеральной совокупности.

Например, при обследовании на предмет успеваемости по физиологии студентов медицинских институтов А, В и С, в которых обучаются 500, 200 и 300 студентов, соответственно, выборку объемом 100 следует строить так, чтобы в нее входило 50 случайным образом выбранных студентов института А, 20 студентов института В и 30 студентов института С. Говоря короче, пропорции в выборке должны соответствовать пропорциям генеральной совокупности.

Для обеспечения репрезентативности выборка должна быть достаточно объемной с тем, чтобы охватывать всю генеральную совокупность, и производиться беспристрастно по отношению к отдельным ее частям. Последнее в определенной мере обеспечивается случайностью отбора элементов выборки.

В дальнейшем мы будем придерживаться простой и надежной схемы, в соответствии с которой интересующая нас характеристика объектов генеральной совокупности является случайной величиной X с частично или полностью неизвестной функцией распределения, а выборка объема n, по которой эту функцию распределения требуется определить, представляет собой n независимых случайных величин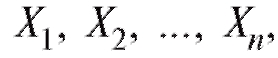 распределенных так же, как X. Такая схема возникает тогда, когда исследователь проводит n независимых друг от друга опытов, в каждом из которых наблюдается некоторое значение одного и того же интересующего его признака, причем предполагается, что во всех n опытах условия эксперимента оставались неизменными. Заметим, что последнее требование достаточно условно и необходимая степень его выполнения устанавливается экспериментатором в соответствии с целями опыта.

Расположив члены выборки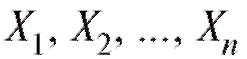(т. е. n чисел в определен-

ных физических единицах) в порядке возрастания, получим вариационный ряд

(8.1)

Пример. Вариационный ряд, полученный по выборке 2, -1, 0, 2, 0, 3, 3, 0, 4, 2, имеет вид -1, 0, 0, 0, 2, 2, 2, 3, 3, 4.

Необходимо отметить, что на деле исследователь располагает не собственно случайной выборкой, а лишь ее реализацией, т. е. набором чисел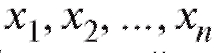(их еще называют вариантами), полученных в результате наблюдений величины X при n независимых повторениях случайного эксперимента в одинаковых условиях. Таким образом, при использовании соответствующих формул математической статистики в них вместо случайных величин X_k следует подставлять их конкретные реализации x_k. Однако в дальнейшем, чтобы не загромождать изложение материала, мы, как правило, будем обозначать посредством X_k как случайную величину, так и ее значение.

8.1.2. Статистическое распределение выборки

Пусть в выборке объема n из некоторой генеральной совокупности варианты принимаютразличных упорядоченных по возрастанию значенийпричем значения x_k встречаются n_k раз. Числа

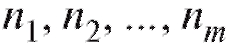называются частотами вариант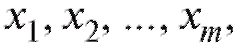соответствен-

но, а величины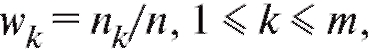их относительными частотами.

Очевидно, что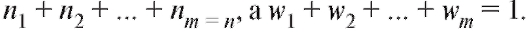

Определение. Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называется набор вариант x_k и соответствующих им частот n_k или относительных частот w_k.

Статистическое распределение выборки удобно представлять в форме таблицы распределения частот (частотной таблицы), иногда называемой статистическим рядом распределения (табл. 8.1), или в виде таблицы распределения относительных частот (табл. 8.2).

Таблица 8.1

Таблица 8.2

Отметим, что с формальной точки зрения табл. 8.2 описывает закон распределения некоторой гипотетической дискретной случайной величины.

Графическими аналогами табл. 8.1 и 8.2 являются столбцовые диаграммы (рис. 8.1 и 8.2), т. е. последовательности вертикальных отрезков (ординат) длины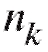или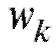с абсциссами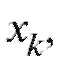k = 1, 2, ... , m, которые отличаются друг от друга лишь масштабом по оси ординат.

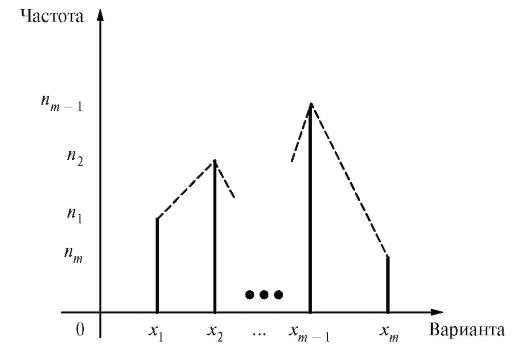
Рис. 8.1. Столбцовая диаграмма для табл. 8.1

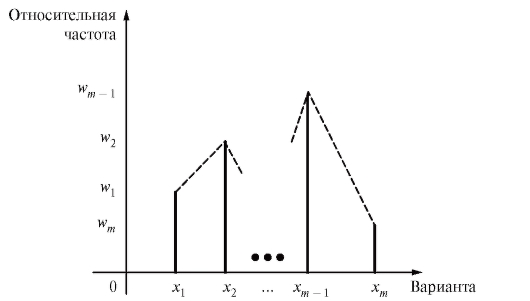
Рис. 8.2. Столбцовая диаграмма для табл. 8.2

Другая эквивалентная форма графического изображения табл. 8.1 и 8.2, называемая полигоном частот (или полигоном относительных частот),

представлена на рис. 8.1 и 8.2 пунктирной линией, соединяющей вершины вертикальных отрезков, т. е. точк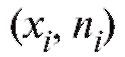иили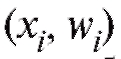соответственно.

Пример. Найти статистическое распределение выборки из примера, приведенного в п. 8.1.1, и представить его в форме таблицы частот и относительных частот. Построить график и полигон относительных частот.

Решение. Статистическое распределение выборки представлено в табл. 8.3, а график и полигон относительных частот изображены на рис. 8.3 и 8.4 соответственно.

Таблица 8.3

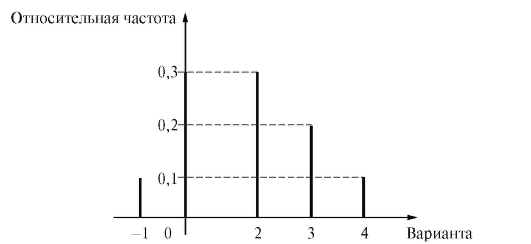
Рис. 8.3. График относительных частот к табл. 8.3

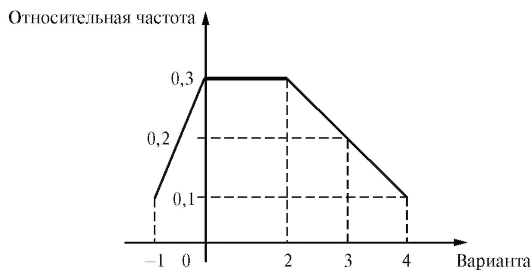
Рис. 8.4. Полигон относительных частот к табл. 8.3

8.1.3. Эмпирическая функция распределения

Определение. Эмпирической функцией распределения, построенной по случайной выборке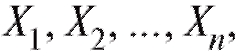называется функция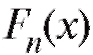, равная доле

тех элементов выборки, которые меньше x, где x - любое вещественное число.

Из приведенного определения следует, что если статистическое распределение выборки задано частотной таблицей (см. табл. 8.1 и 8.2), то

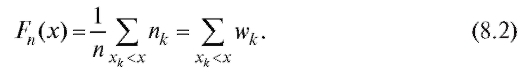
Эмпирическая функция распределения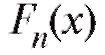обладает всеми свойствами обычной функции распределения, в частности не убывает по x.

Замечание. Если статистическое распределение выборки задано табл. 8.2, то эмпирическая функция распределения равна нулю при

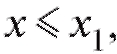равна единице при, если

2, ... , m - 1.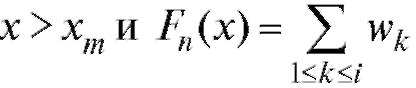

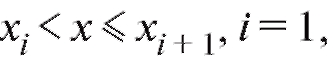
Отметим, что статистическое распределение выборки и ее эмпирическая функция распределения взаимно однозначно определяют друг друга.

Пример. Найти эмпирическую функцию распределения, соответствующую выборке из примера, представленного в п. 8.1.1, и построить ее график.

Решение. Объем выборки равен n = 10, а соответствующая ей частотная таблица есть табл. 8.3. Таким образом, по замечанию, приведенному ранее,

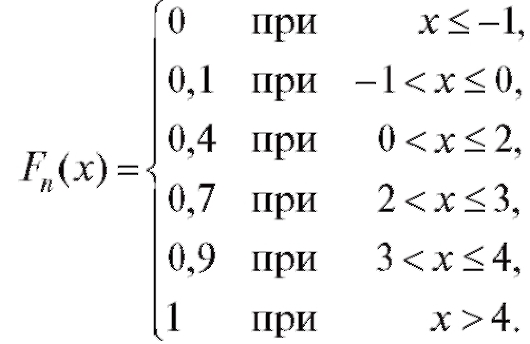
График функции F_n(x) представлен на рис. 8.5.

Репрезентативная выборка подобна генеральной совокупности,

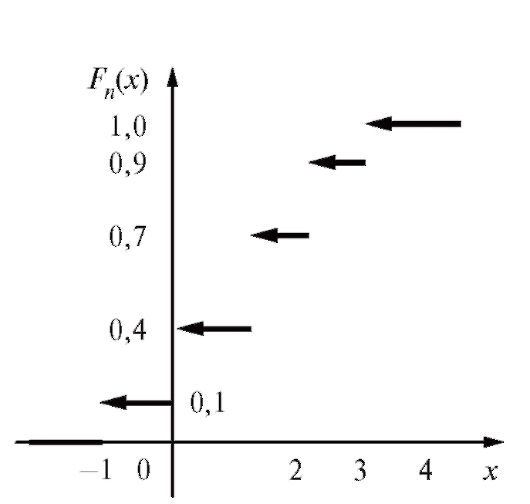
Рис. 8.5. График эмпирической функции распределения

из которой она извлечена, в силу чего эмпирическая функция распределения F_n(x) должна быть в некотором смысле близка к функции распределения F(x) признака X генеральной совокупности. Это действительно так. Методами теории вероятностей доказывается, что эмпирическая функция распределения F_n(x), которая, как и прочие оценки, построенные по случайным выборкам, является случайной величиной, с увеличением объема выборки сходится (в частности по вероятности) к теоретической функции распределения F(x) и является хорошим ее приближением.

8.1.4. Статистический интервальный ряд распределения. Гистограмма

Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются в том случае, когда отличных друг от друга вариант в выборке не слишком много или когда дискретность по тем или иным причинам существенна для исследователя. Если же интересующий нас признак генеральной совокупности X распределен непрерывно или его дискретность нецелесообразно (или невозможно) учитывать, то варианты группируются в интервалы.

Типичная процедура выглядит следующим образом. Чтобы сгруппировать данные, содержащиеся в выборке объема n из наблюдений над случайной величиной X, следует разделить отрезок [а; b], содержащий все варианты, на k интервалов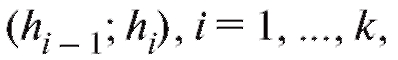

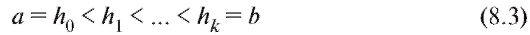
(обычно,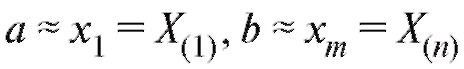(см. табл. 8.1 и 8.2)). Затем надо опре-

делить частоту каждого интервала, т. е. количество наблюдений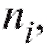попавших в i-й интервал. Для определенности будем полагать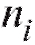равным числу вариант, принадлежащих полуинтервалу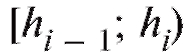, включая все

варианты, попавшие на правую границу, т. е. равные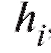, в следующий промежуток во всех случаях, кроме последнего. Количество интервалов k, а также значения их границ h_i до некоторой степени произвольны и являются компромиссом между требованиями экономии и точности.

Замечание. Часто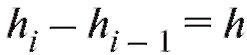при всех i, т. е. группировку осущест-

вляют с равным шагом h. В этой ситуации можно руководствоваться следующими эмпирическими рекомендациями по выбору a, k и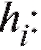

• k - наименьшее целое такое, что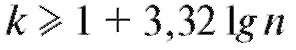(так, если n = 50, то k = 7);

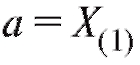• (или чуть меньше);

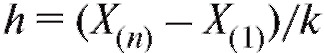• (или чуть больше);

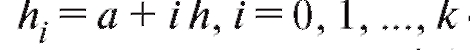•(в частности b = a + k h). Так же, как и ранее в п. 8.1.2, полученную группировку удобно представить в форме частотной таблицы, которая носит название статистический интервальный ряд распределения (табл. 8.4).

Таблица 8.4

(Граничная точка h_k включается в последний интервал, чтобы избежать проблем в случае, когда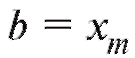(см. (8.3).) Аналогичную таблицу можно образовать, заменяя в табл. 8.4 частоты n_i относительными частотами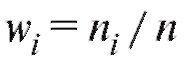(табл. 8.5).

Таблица 8.5

Напоминаем, что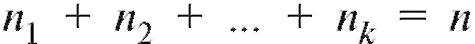 - объему выборки, а

Наиболее информативной графической формой частотной таблицы (см. табл. 8.4) является специальный график, называемый гистограммой частот.

Гистограмма частот состоит из прямоугольников с основаниями 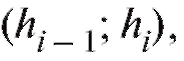высота которых равна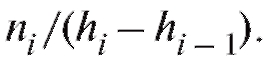Таким образом, площадь

каждого прямоугольника равна n_i, а их сумма равна n.

Аналогично определяется графическая форма табл. 8.5 - гистограмма относительных частот, состоящая из прямоугольников с основаниями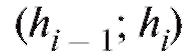и высотамиЗаметим, 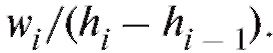что площадь той части гистограммы относительных частот, что лежит между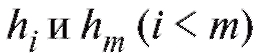, равна относительному числу вариант, попавших в интервал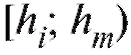, и в соответствии со статистическим определением вероятности может быть интерпретирована как грубая оценка вероятности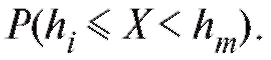Следовательно, с определенными оговорками можно утверждать, что гисто-

грамма относительных частот является выборочным аналогом графика плотности вероятностей распределения признака генеральной совокупности.

Пример. Из очень большой партии огурцов извлечена случайная выборка объемом 50. Интересующий нас признак X - длины огурцов, измеренные с точностью до 1 см - представлен следующим вариационным рядом: 22, 24, 26, 26, 27, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Найти статистический интервальный ряд распределения и построить гистограмму относительных частот с равным шагом.

Решение. Определим характеристики группировки с помощью замечания, приведенного ранее в этом пункте. Имеем a = 22, k = 7,

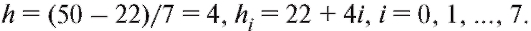Таким образом, частотная таблица представлена в табл. 8.6.

Таблица 8.6

(Напоминаем, что при попадании на границу интервала варианта записывается в правый интервал во всех случаях, кроме последнего.)

Гистограмма относительных частот строится по данным первой и третьей строк табл. 8.6 (рис. 8.6).

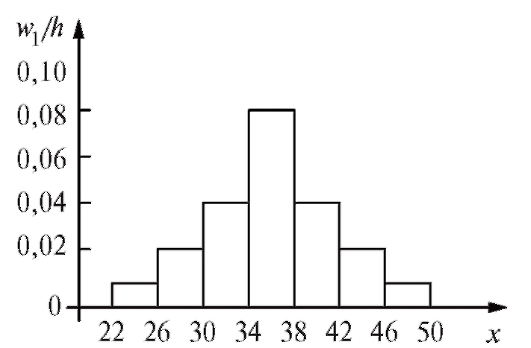
Рис. 8.6. Гистограмма относительных частот к примеру

Самостоятельная работа

1. Построить полигоны частот и эмпирические функции распределения по частотным таблицам (табл. 8.7 и 8.8).

Таблица 8.7

Таблица 8.8

2. Изучалось содержание кальция (мг%) в сыворотке крови больных обезьян. По случайной выборке объемом 50: 9, 10, 8, 7, 9, 10, 10, 10, 8,

7, 8, 7, 10, 7, 8, 6, 8, 10, 7, 6, 8, 5, 7, 7, 8, 8, 8, 9, 5, 9, 7, 7, 7, 8, 7, 7, 9, 6, 11, 9, 8, 8, 7, 7, 5, 11, 8, 6, 8, 8 найти статистический интервальный ряд распределения и построить гистограмму относительных частот.

3. Изучалось содержание кальция (мг%) в сыворотке крови здоровых обезьян. По случайной выборке объемом 44: 8, 10, 8, 8, 9, 8, 5, 6, 7,

8, 9, 7, 8, 9, 8, 8, 7, 7, 8, 9, 11, 9, 8, 8, 9, 10, 7, 9, 7, 8, 8, 8, 7, 7, 7, 8, 7, 7, 9,

8, 6, 10, 8, 10 определить то же, что в предыдущей задаче.

8.2. ОЦЕНКИ ХАРАКТЕРИСТИК РАСПРЕДЕЛЕНИЯ ПО ДАННЫМ ВЫБОРКИ

В ряде практических ситуаций форма закона распределения изучаемой характеристики объектов генеральной совокупности, или случайной величины X, предполагается известной с точностью до одного или нескольких числовых параметров. В таких случаях перед исследователем стоит задача получения оценок этих параметров на основании извлеченной из генеральной совокупности случайной выборки.

Так, центральная предельная теорема позволяет погрешности измерений рассматривать как случайную величину X, распределенную по нормальному закону; в теории надежности систем радиоэлектронной аппаратуры срок службы элемента системы часто рассматривают как случайную величину X, распределенную показательно. В первом случае для нахождения закона распределения X достаточно определить (оценить) два параметра - a и о, во втором - один параметр X.

Ясно, что разумная процедура оценивания не должна ограничиваться лишь выбором приближенного численного значения для неизвестного параметра, но что-то говорить и о надежности этого приближения. Хотя эти два аспекта единой проблемы тесно связаны, удобно обсуждать их отдельно. Соответственно мы будем говорить о точечном оценивании (см. п. 8.2.1) и об интервальном оценивании (см. п. 8.2.2).

8.2.1. Точечные оценки

Пусть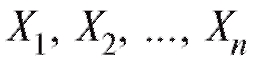- выборка, отвечающая случайной величине X

с функцией распределения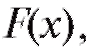относительно которой предполагается, что она зависит от некоторого неизвестного параметра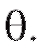Таким параметром может быть генеральное среднее, т. е. математическое ожидание M(X), или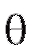генеральная дисперсия, т. е. дисперсия D(X). Требуется оценить параметрпо наблюдениям выборки.

Назовем оценкой неизвестного параметра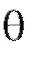величину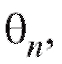зависящую от наблюдений выборки и приближенно равную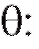

(такого рода оценки параметров распределений называют точечными). Заметим, что оценка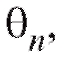как функция выборки, является случайной величиной и будет меняться от выборки к выборке.

Для того чтобы хорошо аппроксимировать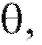оценка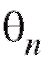в соответствии с требованиями математической статистики должна удовлетворять ряду критериев, основными из которых являются состоятельность и несмещенность.

Определение. Оценка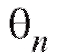называется состоятельной оценкой параметра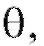если при

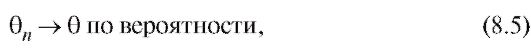
т. е.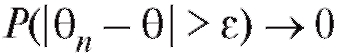при любом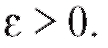

Другими словами, вероятность отклонения оценки от истинного значения параметра можно сделать сколь угодно малой, увеличивая объем выборки.

Определение. Оценка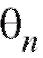называется несмещенной оценкой параметра 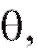если при любом n

Последнее означает, что отклонение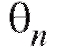от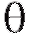не содержит систематической ошибки.

Если равенство (8.6) не выполняется, оценка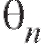называется смещенной.

Поскольку наиболее важными числовыми характеристиками большинства случайных величин являются их математические ожидания и дисперсии, далее приведем точечные оценки этих параметров.

В качестве оценки математического ожидания M(X) используется оценка

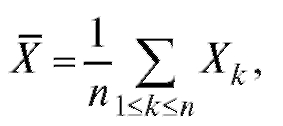(8.7)

называемая выборочным средним.

Оценкой дисперсии D(X) является так называемая исправленная выборочная дисперсия

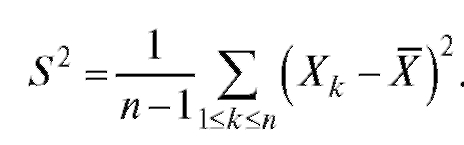(8.8)

Можно показать, что выборочное среднее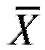 и исправленная выборочная дисперсия S² являются несмещенными состоятельными оценками генерального среднего M(X) и генеральной дисперсии D(X) соответственно.

Наряду с оценкой дисперсии (8.8) в математической статистике используется также выборочная дисперсия

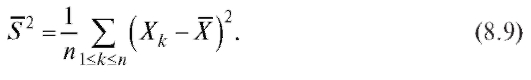
Таким образом,

Заметим, что оценка (8.9) в отличие от оценки (8.8) является смещенной, хотя и состоятельной, оценкой генеральной дисперсии, причем занижает (и довольно существенно в случае малых n) ее величину (наличие в определении исправленной выборочной дисперсии множителя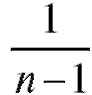вызвано именно требованием несмещенности).

Замечание. Если известен статистический закон распределения выборки (см. табл. 8.1 и 8.2), то оценки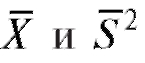можно вычислить по формулам:

(8.11) 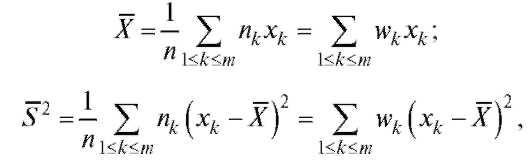(8.12)

где (см. п. 8.1.2)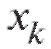- набор всех отличающихся друг от друга вариант и соответствующих им частот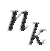или относительных частот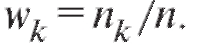

Равенство (8.12) может быть записано в следующем более удобном для расчетов виде:

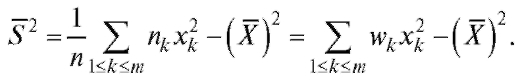(8.13)

Пример. По статистическому распределению выборки из примера, рассмотренного в п. 8.1.2, найти несмещенные оценки генерального среднего и генеральной дисперсии.

Решение. Для нахождения оценки генерального среднего воспользуемся формулой (8.11) и данными табл. 8.3. Имеем при n = 10

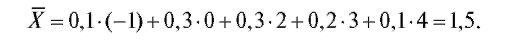
Оценку генеральной дисперсии вычисляем по формулам (8.10) и

(8.13):

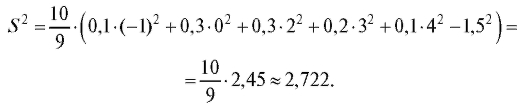
8.2.2. Интервальные оценки

Пусть, как и в предыдущем пункте,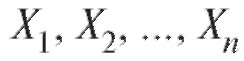- выборка, отвеча-

ющая случайной величине X с функцией распределения F(x), зависящей от некоторого параметра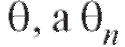- несмещенная и состоятельная оценка

этого параметра. Поскольку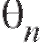является случайной величиной, желательно уметь оценивать «качество» равенства (8.4) с тем, чтобы иметь представление о том, к каким ошибкам может привести замена параметра 9 его точечной оценкой и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы. Для ответа на эти вопросы в математической статистике вводится понятие доверительного интервала.

Пусть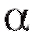- некоторое число из интервала (0; 1), а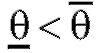- две функции, зависящие от выборки.

Определение. Интервал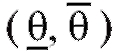называется доверительным интерва-

лом для оценки параметра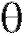, отвечающим доверительной вероятности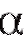, если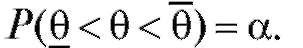

Иными словами, доверительный интервал - это интервал со случайными границами, который накрывает оцениваемый параметр с наперед заданной вероятностью. При этом границы доверительного интервала будут зависеть от вариант, объема выборки и доверительной вероятности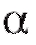(заметим, что число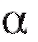обычно выбирается достаточно близким к единице; в фармации, как правило, полагают= 0,95 или 0,99).

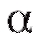
С практической точки зрения можно утверждать, что если мы извлечем из генеральной совокупности, скажем, 100 случайных выборок одинакового объема и построим по ним соответствующие доверительные интервалы (с одной и той же доверительной вероятностью), то следует ожидать, что приблизительно в 100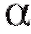случаях (если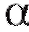= 0,95, то в 95-ти) эти интервалы будут содержать параметр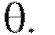

Рассмотрим методы построения доверительного интервала для генерального среднего M (X), предполагая, что интересующая нас характеристика объектов X генеральной совокупности, как это часто бывает на практике, имеет нормальное распределение, т. е.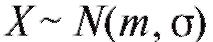(напомина-

ем, что в этом случае математическое ожидание M (X) = m, а дисперсия

).

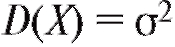Сначала рассмотрим случай известной дисперсии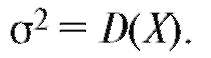

Теорема 8.1. Доверительным интервалом с доверительной вероятностью а для неизвестного математического ожидания m = M (X) при известной дисперсии о² является случайный интервал

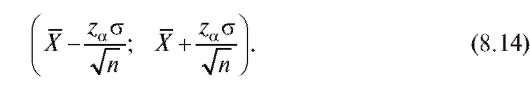
Здесь z_a является решением уравнения

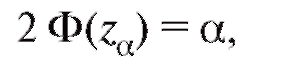
Ф(х) - функция Лапласа (см. (7.33)), численные значения которой приведены в приложении 1. В частности составим табл. 8.9.

Таблица 8.9

Доказательство теоремы 8.1 опирается на следующий факт из теории вероятностей: случайная величина

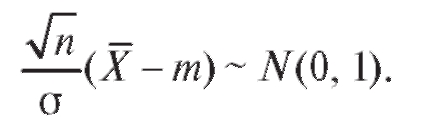
Пример 1. Отобранные случайным образом из некоторой популяции (генеральной совокупности) 10 крыс откармливались по специальному рациону. Прибавление веса регистрировалось и по прошествии определенного периода оказалось следующим: 113,4, 112,0, 88,6, 49,1, 133,7, 57,8, 44,2, 124,3, 89,5, 93,4. Предполагая, что прибавление веса имеет нормальное распределение со среднеквадратичной ошибкой 40, определить доверительный интервал с доверительной вероятностью 0,95 для среднего прибавления веса в популяции крыс при этом рационе.

Решение. Применим теорему 8.1 при n = 10,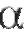= 0,95 и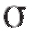= 40. Учитывая, что в данном примере выборочное среднее 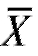= 90,6, а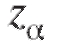= 1,96, найдем границы искомого случайного интервала (см. соотношение (8.14)): 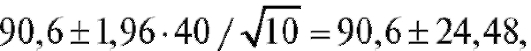и сам доверительный интер-

вал - (66,12; 115,4). Таким образом, при изучении большого числа выборок по 10 крыс в каждой в предполагаемых условиях вычисленный в результате интервал должен в 95 % случаев включать истинное среднее прибавление веса в популяции крыс.

Обратимся теперь к более естественной ситуации, когда оба параметра нормального распределения m и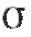предполагаются неизвестными.

Теорема 8.2. Доверительным интервалом с доверительной вероятностью а для неизвестного математического ожидания m = M (X) при неизвестной дисперсии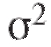является случайный интервал

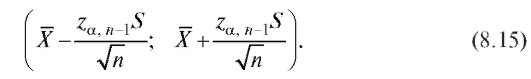
Здесь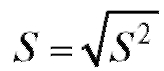 (см. (8.8)),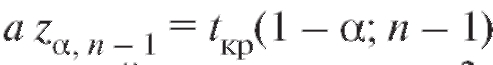, где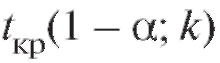

можно определить по приведенной в приложении 2 таблице правых критических точек распределения Стьюдента с k = n - 1 степенями свободы, отвечающих уровню значимости 1 - а (двусторонняя критическая область).

Замечание 1. Последовательность значений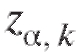убывает с ростом k, и 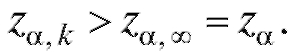Это приводит к тому, что в типичных случаях длина доверительного интервала (8.15) больше длины доверительного интервала

(8.14).

При доказательстве теоремы 8.2 используется то, что случайная величина 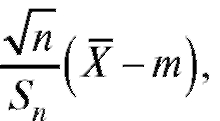где S² - исправленная выборочная дисперсия,

определенная в (8.8), имеет распределение, не зависящее от параметров m и о нормального распределения, из которого извлекается выборка. В курсе математической статистики доказывается, что указанное распределение, называемое распределением Стьюдента, имеет симметричную относительно нуля плотность, которая с ростом n быстро сходится к плотности нормального распределения N(0, 1).

Пример 2. Найти доверительный интервал с доверительной вероятностью 0,95 для среднего прибавления веса в популяции крыс по выборке из примера 1, рассмотренного ранее в этом пункте, считая, что генеральная дисперсия неизвестна.

Решение. Исправленная выборочная дисперсия S² по данным примера 1, рассчитанная по формуле (8.8), равна 992,8. Применяя теорему 8.2 и учитывая, что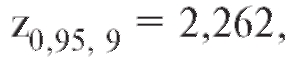найдем границы случайного интервала

(см. (8.15)):

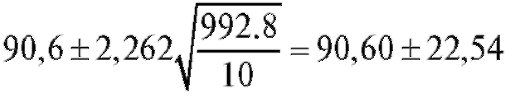
и сам доверительный интервал (68,06; 113,14).

Замечание 2. При построении доверительных интервалов (8.14) и (8.15) предполагается, что варианты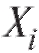имеют нормальное распределение 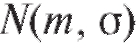, что предопределяет одно из основных достоинств доверительных интервалов - их неасимптотический характер (теорема 8.1 имеет место при любом, а теорема 8.2 - при любом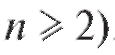. При большом n, однако, можно строить приближенные доверительные интервалы для неизвестного математического ожидания m = M (X) без предположения нормальности. Так, случайный интервал

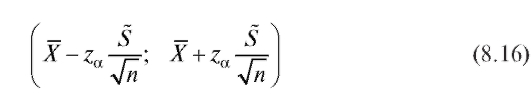
является доверительным интервалом для математического ожидания m с доверительной вероятностью, приблизительно равной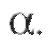Здесь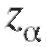- то же, что в (8.14), а в качестве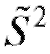может выступать какая-либо состоятельная оценка дисперсии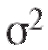, например S² или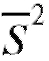

8.2.3. Статистические оценки случайных погрешностей измерений

Измерения неизвестных величин приходится осуществлять в самых различных областях человеческой деятельности. При этом результаты измерений X₁, X₂, ... , X_n одной и той же величины, как правило, несколько отличаются друг от друга, так как невозможно полностью воспроизвести условия проведения различных измерений. Общая ошибка измерения часто складывается из большого числа незначительных ошибок. Если измерительный прибор не дает систематической ошибки, то в такой ситуации (с учетом центральной предельной теоремы) становится правдоподобным предположение, что каждое отдельное измерение X_i можно представить в виде суммы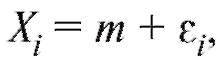где m представляет неизвестное истинное значение измеряемой величины,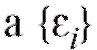являются независимыми нормально распределенными случайными ошибками с нулевыми средними (следствие отсутствия систематической ошибки) и некоторыми одинаковыми, вообще говоря, неизвестными дисперсиями 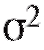(таким образом,).

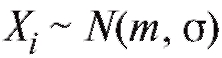Другими словами, наблюдаемые величины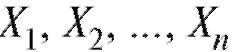можно счи-

тать случайной выборкой объема n из генеральной совокупности всевозможных, проведенных в одних и тех же условиях, измерений интересующей нас случайной величины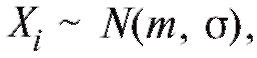и применять для их обработки такие статистические методы, как точечное и интервальное оценивание, и, в частности, использовать теоремы 8.1 и 8.2.

Принимая во внимание вышесказанное, будем считать, что справедливы следующие утверждения: если в одних и тех же условиях осуществлено n независимых измерений некоторой интересующей нас величины, точное значение m которой неизвестно, и результаты этих измерений обозначены через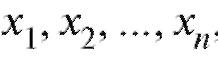то

где величина X определена формулой

кроме того, с доверительной вероятностью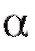истинное значение m содержится в интервале

где

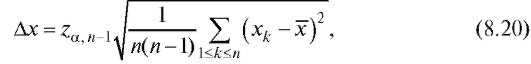
а множитель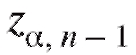такой же, как в (8.15).

Отметим, что величину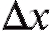называют абсолютной погрешностью измерений, а соотношение (8.19) обычно записывают как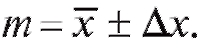

Наряду с абсолютной погрешностью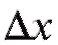используют также относительную погрешность

Пример. Произведено пять независимых измерений веса таблетки лекарственного вещества. Получены следующие значения (в миллиграммах, мг): 159,4, 159,7, 159,6, 159,3, 159,0.

Предполагая, что ошибки измерения распределены по нормальному закону, оценить истинный вес таблетки и найти погрешности его измерения при доверительной вероятности 0,99.

Решение. Для решения задачи воспользуемся формулами (8.17)- (8.21). Имеем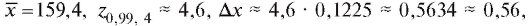

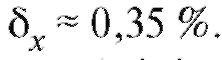Таким образом, истинный вес таблетки m оценивается числом 159,4. Кроме того,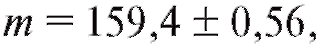т. е. с доверительной вероятностью 0,99 истинный вес таблетки может колебаться в пределах от 158,84

до 159,96.

Самостоятельная работа

1. По данным заданий 1 и 2 из самостоятельной работы к п. 8.1 найти выборочные средние и выборочные дисперсии, а также приближенные доверительные интервалы для математических ожиданий с доверительной вероятностью 0,95.

2. При измерении содержания кальция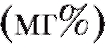в сыворотке крови подопытных животных получили следующие результаты: 14,5, 14,7, 14,8, 14,9, 15,1, 15,3, 15,5, 15,8, 15,9. Определить доверительный интервал для среднего значения содержания кальция с доверительной вероятностью 0,9 (предполагается, что показатель распределен по нормальному закону).

3. При подсчете количества листьев у шести лекарственных растений одного вида были получены следующие результаты: 5, 8, 10, 11, 12,

14. Определить доверительный интервал для среднего числа листьев с доверительной вероятностью 0,95 (предполагается, что показатель распределен по нормальному закону).

4. По данным девяти равноточных измерений физической величины 34, 40, 45, 43, 39, 41, 37, 48, 36 оценить ее истинное значение m и найти его абсолютную погрешностьпри доверительной вероятности 0,95 (предполагается, что погрешности измерения распределены по нормальному закону).

8.3. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И СГЛАЖИВАНИЕ

ЭКСПЕРИМЕНТАЛЬНЫХ ЗАВИСИМОСТЕЙ

Предположим, что результаты некоторого эксперимента систематизированы в виде табл. 8.10, в которой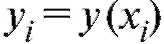является функцией, а x - аргументом, и требуется сгладить эту, заданную таблично, зависимость многочленом или некоторой другой функцией, известной нам с точностью до нескольких подлежащих определению параметров.

Таблица 8.10

Задача сглаживания экспериментальных зависимостей достаточно типична для практики. Решая эту задачу, обычно рассчитывают освободить экспериментальные данные от случайных ошибок, допущенных в каждом отдельном опыте, и свести большое количество этих данных к нескольким параметрам (в частности к коэффициентам многочлена), одновременно получив возможность обрабатывать полученную функциональную зависимость аналитически (например, дифференцировать).

Отметим, что практически любая табличная зависимость может быть сглажена различными функциями с приблизительно одинаковой точностью. В этой связи сглаживающую функцию следует выбирать, исходя из физических соображений, а при отсутствии таковых использовать наиболее простые варианты формул с минимальным числом подлежащих определению коэффициентов. Определенную помощь в выборе сглаживающей функции может также оказать графическое представление табл. 8.10 (рис. 8.7).

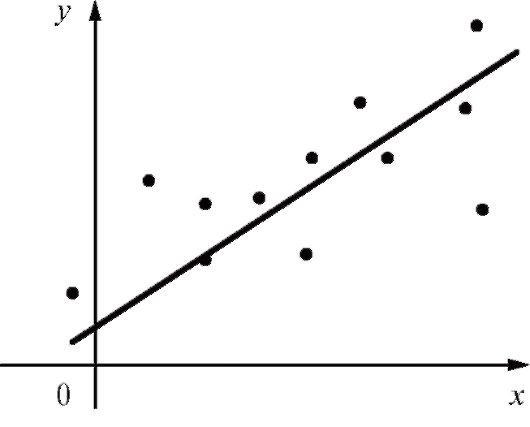
Рис. 8.7. Графическое представление табл. 8.10

Пусть, для определенности, функция, с помощью которой будет осуществляться сглаживание, является многочленом

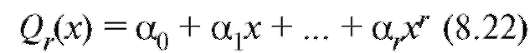
известной степени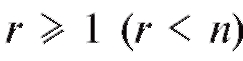 с

числовыми коэффициентами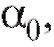

подлежащими определению.

Составим разности

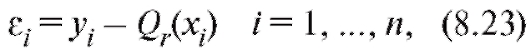
характеризующие близость табличных данных и значений, полученных при помощи сглаживающей функции. Нам следует подобрать коэффициенты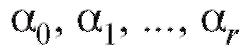таким образом, чтобы величиныв 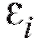совокупности были минимальными.

Эффективной процедурой для решения подобного рода задач является так называемый метод наименьших квадратов, который гласит, что наилучшими во многих отношениях оценками для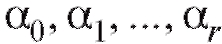являются

оценки, минимизирующие сумму квадратов разностей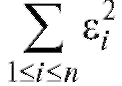 Иными

словами, в качестве оценки для неизвестных параметров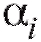следует взять такие значения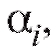при которых функция

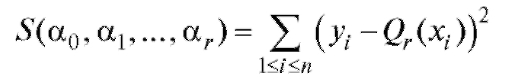
достигает минимума. Поскольку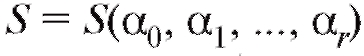представляет диф-

ференцируемую функцию r переменных, необходимым условием ее минимизации является равенство нулю частных производных ,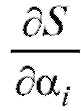

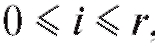вычисленных приРешение системы из r + 1

нормального уравнения

в типичных случаях единственное, дает нам искомые коэффициенты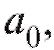

Рассмотрим более детально линейную аппроксимацию экспериментальных зависимостей между величинами, т. е. сглаживание с помощью функции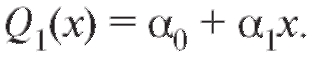В этом случае

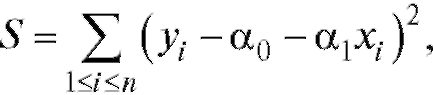
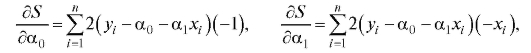
вследствие чего система нормальных уравнений принимает вид

(8.25) Положим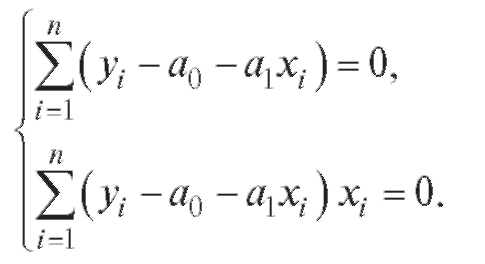

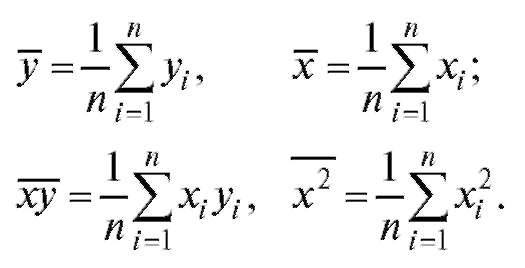(8.26)

Тогда уравнения (8.25) можно переписать в виде системы двух линейных уравнений с двумя неизвестными

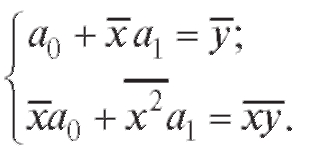(8.27)

Решив эту систему, найдем

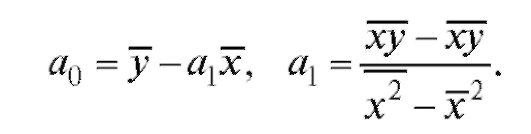(8.28)

Таким образом, наилучшая в смысле метода наименьших квадратов линейная сглаживающая функция выражается уравнением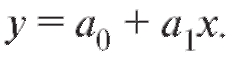

Замечание 1. Сумма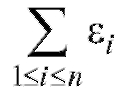оптимальных разностей равняется нулю,

что может быть использовано для контроля правильности вычислений.

Пример 1. Сгладить линейной зависимостью от x данные, приведенные в табл. 8.11. Вычислить разности и отобразить на графике табличные данные и сглаживающую прямую.

Таблица 8.11

Решение. Используя формулы (8.26), найдем , ,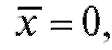

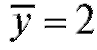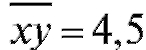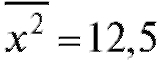и, следовательно,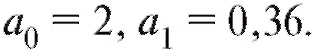Таким образом, уравнение

сглаживающей прямой имеет вид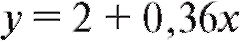(рис. 8.8). Теперь допол-

ним табл. 8.9 и в результате получим табл. 8.12.

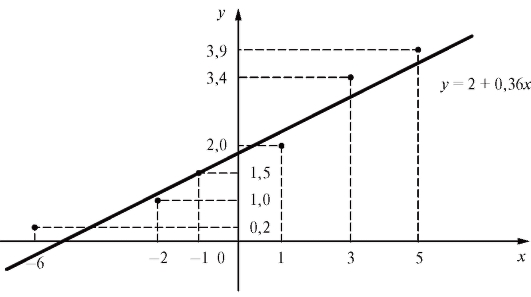
Рис. 8.8. График сглаживающей прямой Таблица 8.12

Заметим, что сумма разностей равна нулю.

Замечание 2. Метод наименьших квадратов можно с некоторой потерей в точности использовать для сглаживания функциональных зависимостей, приводящихся к линейной с помощью замены переменных. Так, зависимость 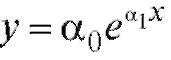может быть переписана в виде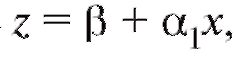

где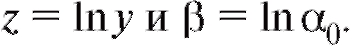Применяя метод наименьших квадратов для на-

хождения коэффициентов линейного уравнения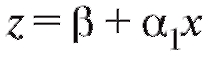и возвраща-

ясь к первоначальной зависимости, получим в качестве оценки коэффициента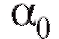величину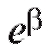(оценка

для o₁ в данном случае остается без изменений).

Пример 2. Пусть данные некоторых измерений представлены в табл. 8.13.

Таблица 8.13

Требуется сгладить их при помощи формулы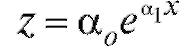и вычислить

разности между табличными и сглаженными значениями с точностью до тысячных.

Решение. Воспользуемся замечанием 2. 1) Заменим числа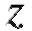из табл. 8.13 числами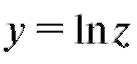(табл. 8.14).

Таблица 8.14

2) По формулам (8.26) и (8.28) найдем коэффициенты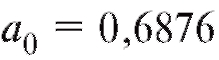 и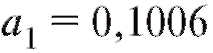линейного уравнениянаилучшим 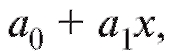образом приближающего y.

3) Учитывая, что коэффициенты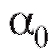и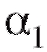связаны с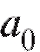и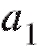соотношениями 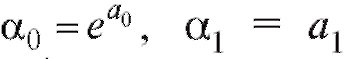окончательно получим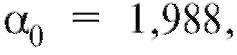

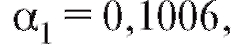и, следовательно, 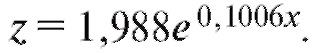Разности между табличными и сглаженными значениями z сведены в табл. 8.15.

Таблица 8.15

Заметим, что сумма разностей здесь отлична от нуля.

Самостоятельная работа

Используя метод наименьших квадратов, сгладить с помощью функций заданного вида следующие табличные зависимости:

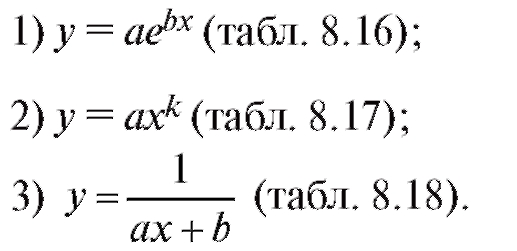
Таблица 8.16

Таблица 8.17

Таблица 8.18

Примечание. Перед использованием метода наименьших квадратов сглаживающие зависимости следует линеаризовать (по параметрам a, b или a, k, используя в первых двух случаях операцию логарифмирования, а в третьем случае взяв 1/y вместо у).

8.4. ЭЛЕМЕНТЫ КОРРЕЛЯЦИОННОРЕГРЕССИОННОГО АНАЛИЗА

Объекты ряда генеральных совокупностей обладают несколькими подлежащими изучению признаками X, Y, которые можно интерпретировать, как систему взаимосвязанных величин. Примерами являются:

• масса животных (X) и количество гемоглобина (Y) в их крови;

• рост (X) мужчины и объем (Y) его грудной клетки;

• количество (X) вводимого объекту препарата и его концентрация в крови (Y).

Отметим, что в двух первых примерах как X, так и Y представляют собой случайные величины, а в третьем - параметр X не является случайным, поскольку экспериментатор может его контролировать. Очевидно, что в приведенных примерах величины Y и X не связаны функционально, поскольку на значения, принимаемые случайной величиной Y, влияют помимо X многие другие факторы, и в то же время не являются независимыми.

В таких случаях говорят, что Y и X связаны стохастической (т. е. случайной) зависимостью.

Понятие стохастической зависимости обобщает понятие функциональной (или детерминированной) зависимости, подобно тому как понятие случайной величины обобщает понятие (детерминированной) величины.

В дальнейшем в основном будем исследовать зависимость между двумя признаками X и Y объектов генеральной совокупности, где случайная величина Y играет роль функции, а X - случайного или детерминированного аргумента. Кроме того, мы ограничимся частным случаем стохастической зависимости величин X и Y, а именно регрессионной зависимостью, при которой изменение величины X влечет изменение математического ожидания (см. п. 8.4.1) случайной величины Y

8.4.1. Линейная и полиномиальная регрессии

Во многих экспериментальных исследованиях вид зависимости между различными величинами можно, в той или иной степени, выявить лишь посредством ряда наблюдений. Рассмотрим достаточно типичный случай. Предположим, что изучается зависимость между величинами x и Y (скажем, затратами на функционирование и величиной годовой прибыли некоторой аптеки), и из условий эксперимента следует, что при значениях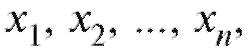известных с устраивающей исследователя

точностью, соответствующие значения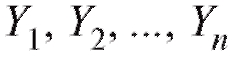определяются с не-

которыми несистематическими (т. е. имеющими нулевое среднее) случайными ошибками (мы специально используем обозначение x, а не X, чтобы подчеркнуть тот факт, что величина x не является случайной). Будем считать, что наблюдаемые величины Y_i представимы в виде

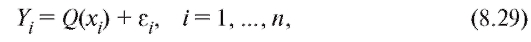
где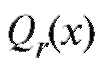- некоторая функция, определенная с точностью до 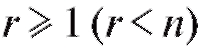неизвестных нам числовых параметров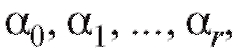а ошибки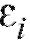- неза-

висимые случайные величины с нулевыми средними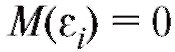и конеч-

ными одинаковыми дисперсиями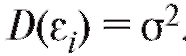

Из условия (8.29) следует, что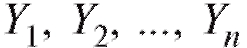являются независимы-

ми случайными величинами, дисперсии которых одинаковы, а средние значения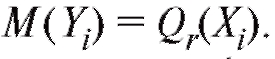

Заметим, что вид функции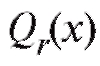должен быть определен заранее, из физических или иных соображений. Определенной подсказкой здесь может служить корреляционное поле точек (см. рис. 8.7 при y = Y), т. е. графическое представление наблюдений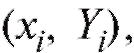дающее возможность

визуально оценить с каким типом зависимости (линейной, экспоненциальной и т. п.) между величинами x и Y мы имеем дело. В дальнейшем будем считать, что

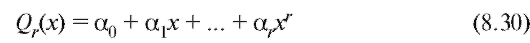
- многочлен известной степени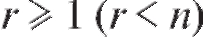с неизвестными нам число-

выми коэффициентами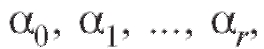т. е.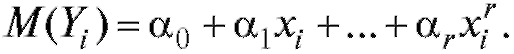

Такая модель носит название полиномиальной регрессионной. Если 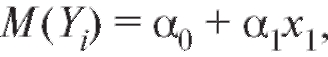говорят о линейной регрессии. Нам требуется по наблюдениям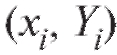определить коэффициенты ре-

грессии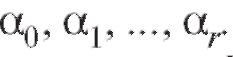

Поскольку ошибки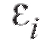в равенстве (8.29) предполагаются случайными, а число уравнений n больше числа параметров r, подлежащих определению, поставленная задача не имеет единственного решения. Мы можем лишь оценить неизвестные параметры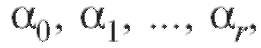используя

содержащуюся в уравнениях (8.29) информацию. С этой целью воспользуемся примененным для решения аналогичной задачи в п. 8.3 методом наименьших квадратов, в соответствии с которым оценками для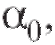

являются оценки, минимизирующие сумму квадратов ошибок

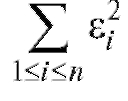
Такая оценка параметров полиномиальной регрессионной модели (подробнее см. п. 8.3, формулы (8.25) и далее) называется оценкой по методу наименьших квадратов (МНК-оценкой). Важно отметить, что в случае полиномиальной регрессионной модели (и вообще, при линейном оценивании) МНК-оценки являются несмещенными (см. (8.6)) и, в некотором смысле, самыми точными.

В случае линейной регрессии, т. е. модели, которая в наших обозначениях имеет вид

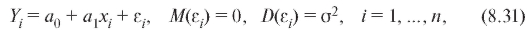
рассуждения, позволяющие вычислить МНК-оценки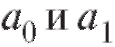для параметров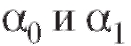из (8.31), дословно совпадают с соответствующими выкладками из п. 8.3. Единственное отличие заключается в том, что в формулах (8.25)-(8.28) следует положить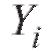вместо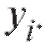Таким образом,

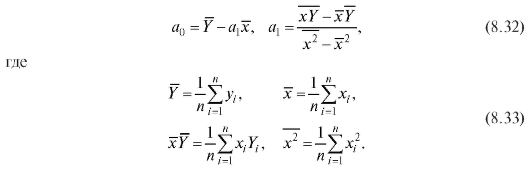
Таблица 8.19

Пример. Предположим, что x - затраты на функционирование и Y - величина годовой прибыли некоторой аптеки в течение 5 лет представлены в условных единицах в табл. 8.19.

Считая, что между затратами и прибылью имеет место линейная зависимость вида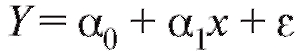c постоянными коэффициентами 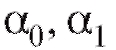и величиной независимого от года к году случайного влияния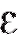с нулевым средним и конечной дисперсией, найти МНК-оценки параметров

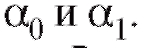
Решение. Зависимость Y от x, представленная по годам, имеет вид

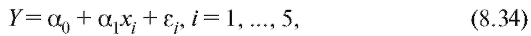
т. е. описывается линейной регрессионной моделью (8.31). По формулам (8.32) и (8.33) для данных из табл. 8.19 найдем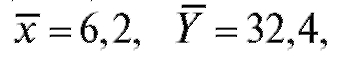

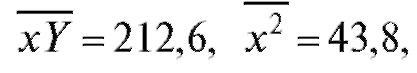откуда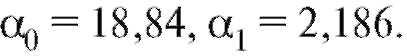

8.4.2. Построение выборочной линии регрессии

В настоящем пункте исследуется случай, когда интересующие нас признаки объектов генеральной совокупности можно рассматривать как двумерный случайный вектор (X, Y) с частично или полностью неизвестным совместным законом распределения. Нашей целью является вычисление статистических оценок основных характеристик этого распределения по наблюдениям выборки из генеральной совокупности и, в частности, выборочной ковариации и выборочного коэффициента корреляции, а также выявление стохастической зависимости между случайными величинами X и Y.

Определение. Случайной выборкой объема n, отвечающей паре случайных величин (X, Y), назовем набор n независимых пар случайных величинкаждая из которых имеет такой же закон

распределения, как и пара величин (X, Y).

Другими словами, случайной выборкой объема n можно считать величины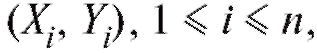полученные в результате n независимых «одинаковых» случайных экспериментов.

Оценками для математических ожиданий M (Y) и M (X), построенными по выборкеявляются хорошо знакомые выборочные средние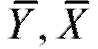случайных величин Y и X соответственно,

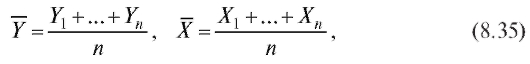
а оценками для дисперсий D(Y), D(X) - исправленные выборочные дисперсии Y и X (см. п. 8.2.1)

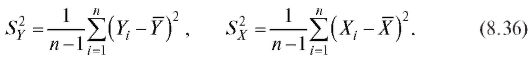
Оценкой для ковариации cov(X, Y) случайных величин X и Y является исправленная выборочная ковариация

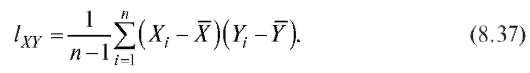
Отметим, что справедливо равенство

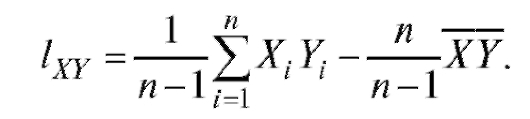
Можно доказать, что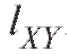является несмещенной состоятельной оценкой ковариации cov(X, Y).

В качестве оценки для коэффициента корреляции r (X, Y) используется выборочный коэффициент корреляции

являющийся состоятельной оценкой коэффициента корреляции.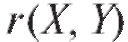

Существенность выборочного коэффициента корреляции приводит к предположению о близкой к линейной зависимости между величинами X и Y. Последнее возможно визуально оценить по виду корреляционого поля точек. Например, корреляционое поле точек, изображенных на рис. 7.11, позволяет высказать гипотезу о линейной регрессии Y на Х, т. е. дает основание рассчитывать на то, что функция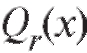в формуле (8.29) имеет вид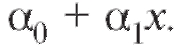Следующей задачей является нахождение оценок коэффициентов регрессии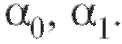Вновь, как и в п. 8.4.1, обратимся к методу наименьших квадратов и будем искать такие значения 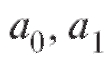величин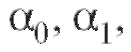которые минимизируют сумму

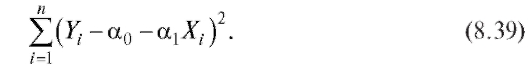
Имеем (см. формулы (8.35) и (8.32), (8.33) с заменой в их обозначениях x на X)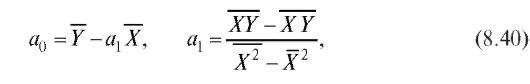

где использованы обозначения

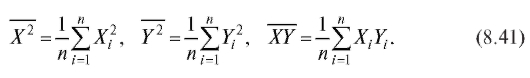
Принимая во внимание формулы

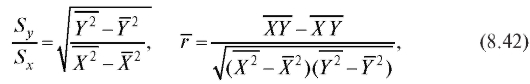
видим, что выборочное уравнение прямой средней квадратической регрессии Y на X имеет вид

и отличается от своего теоретического аналога (7.46) лишь заменой параметров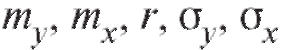их оценками. То же можно сказать о выборочном уравнении прямой среднеквадратической регрессии X на Y

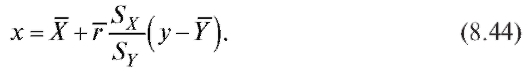
Отметим, что прямые, имеющие уравнения (8.43) и (8.44), проходят через точку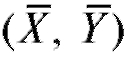, а их угловые коэффициенты совпадают по знаку с

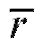и что в практическом плане коэффициенты этих уравнений удобно вычислять при помощи формул (8.42).

Пример 1. Изучалась зависимость между систолическим давлением Y мужчин в начальной стадии шока и возрастом X. Результаты наблюдений приведены в табл. 8.20 в виде двумерной выборки объемом 11.

Таблица 8.20

Требуется вычислить выборочный коэффициент корреляции и найти выборочное уравнение линейной регрессии Y на X.

Решение. Применяя формулы (8.41) и (8.33) с X вместо х, найдем, округляя до сотых:

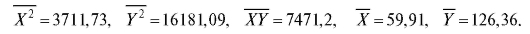
Отсюда по (8.42) и (8.40)

Таким образом, выборочное уравнение прямой средней квадратической регрессии Y на X имеет вид y = 174,89 - 0,81x.

Если объем n выборки достаточно велик, то перед нахождением тех или иных статистических оценок по наблюдениям выборки ее обычно сводят в корреляционную таблицу (табл. 8.21).

Таблица 8.21

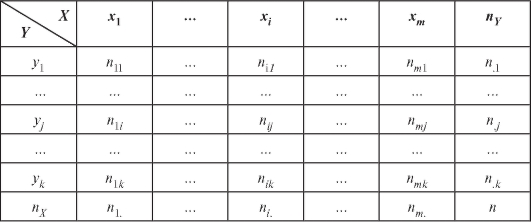
Здесь:

• сумма элементов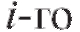столбца

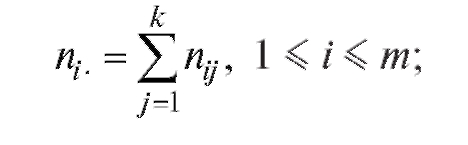
• сумма элементов j-й строки

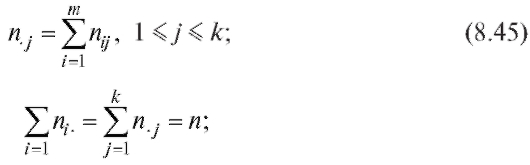
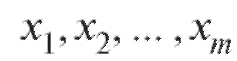•- середины интервалов группировки (см. п. 8.1.4) по X;

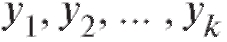• - середины интервалов группировки по Y;

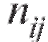• - число точек выборки, попавших в прямоугольник с центром

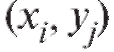
Как правило, группировка осуществляется с равным шагом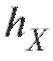по X и равным шагом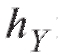по Y, т. е.

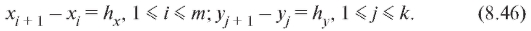
Аналоги формул (8.35) и (8.41), полученные по данным корреляционной таблицы, выглядят так:

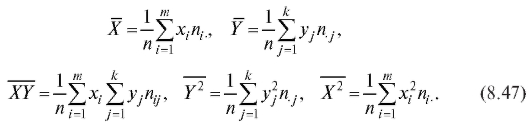
Оценки дисперсий и ковариации рассчитываются по формулам:

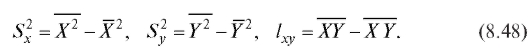
Выборочный коэффициент корреляции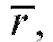выборочные коэффициенты регрессии а₀, а₁ и выборочные уравнения прямой средней квадратической регрессии находятся по тем же формулам (8.38), (8.40), (8.43) и (8.44), что и ранее, с учетом обозначений (8.47) и (8.48). Напоминаем, что при вычислениях удобно пользоваться равенствами (8.41).

Замечание. Для упрощения вычислений в табл. 8.21 удобно от перейти к новым переменным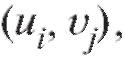положив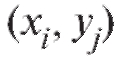

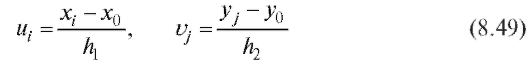
и выбирая числа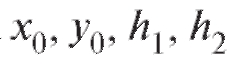таким образом, чтобы по формулам (8.47),

(8.48), в которых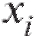заменено на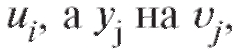было проще считать (при

условии (8.46), например, удобно положить,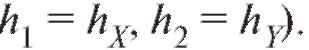Обратный

пересчет осуществляется по формулам

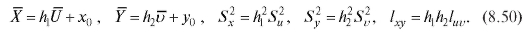
Таблица 8.22

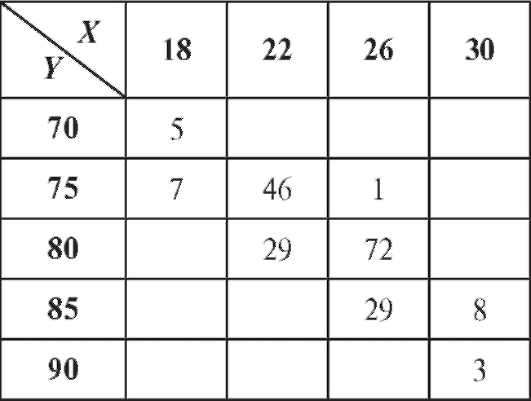
Таблица 8.23

Заметим, что при линейном преобразовании (8.49) значение выборочного коэффициента корреляции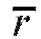не изменяется.

Пример 2. Изучалась зависимость между количеством гемоглобина в крови Y (%) и массой животных X (кг). Результаты наблюдений приведены в виде корреляционной таблицы (пропуски означают нули) - табл. 8.22.

Требуется определить выборочный аналог уравнения прямой средней квадратической регрессии Y на X.

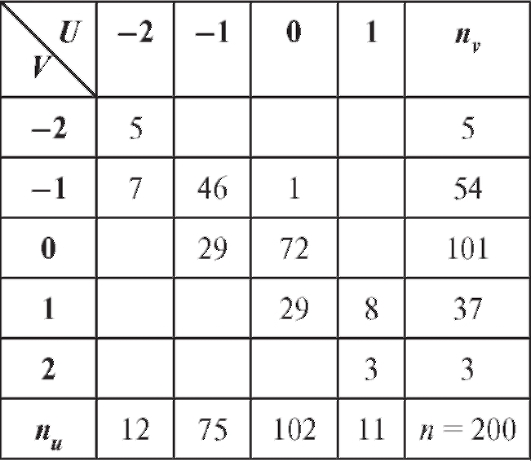
Решение. Для упрощения вычислений перейдем к новым переменным U и V, воспользовавшись формулами (8.49) при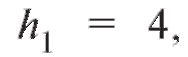

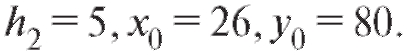Для удобства перепищем табл. 8.22 в новых обозначениях, добавив справа столбец с суммой частот по строкам, а снизу - строку с суммой частот по столбцам (табл. 8.23).

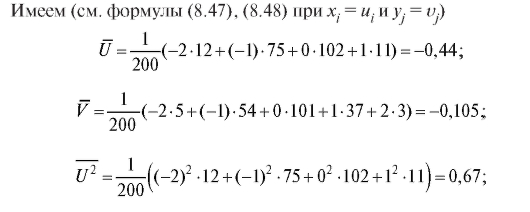
Таким образом (см. формулу (8.50)),

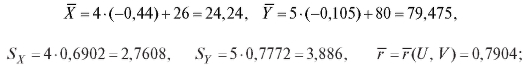
выборочное уравнение прямой средней квадратической регрессии Y на X выражается формулой (8.43):

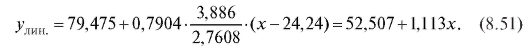
Откуда получаем табл. 8.24. Таблица 8.24

Самостоятельная работа

1. В 100 частях воды растворяется следующее число условных частей азотнокислого натрия NaNO₃ (признак Y) при соответствующих температурах (X) (табл. 8.25).

Таблица 8.25

На количество растворившегося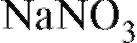влияют случайные факторы.

Предполагается наличие стохастической линейной зависимости между температурой и количеством растворившегося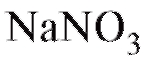вида (8.31). Най-

ти МНК-оценку коэффициентов линейной модели.

2. В задачах, представленных далее, требуется вычислить выборочный коэффициент корреляции между переменными Y и X и найти выборочное уравнение прямой средней квадратической регрессии Y на X. 1) Изучалась зависимость между содержанием коллагена Y и эластина X в магистральных артериях головы (г/100 г сухого вещества) у пациентов в возрасте 51-75 лет. Результаты наблюдений приведены в табл. 8.26 в виде двумерной выборки объемом 5.

Таблица 8.26

2) Изучалась зависимость между массой новорожденных павианов гамадрилов X (кг) и массой их матерей Y (кг). Результаты наблюдений приведены в табл. 8.27 в виде двумерной выборки объемом 9.

Таблица 8.27

3) Изучалась зависимость между объемом грудной клетки мужчин Y (см) и ростом X (см). Результаты наблюдений приведены в табл. 8.28 в виде двумерной выборки объемом 7.

Таблица 8.28

4) Изучалась зависимость между минутным объемом сердца Y (л/ мин) и средним давлением в левом предсердии X (мм рт. ст.). Результаты наблюдений приведены в табл. 8.29 в виде двумерной выборки объемом 5.

Таблица 8.29

3. По табл. 8.30-8.33 сгруппированных данных вычислить выборочный коэффициент корреляции X и Y и написать уравнение линейной регрессии Y на X.

Таблица 8.30

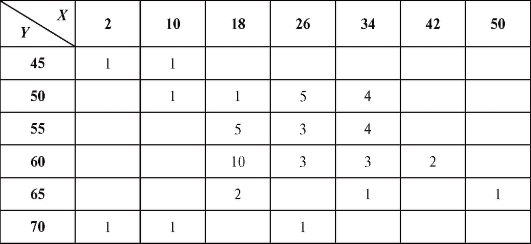
Таблица 8.31

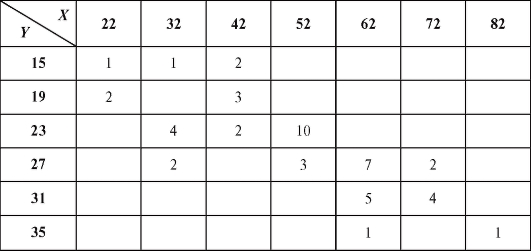
Таблица 8.32

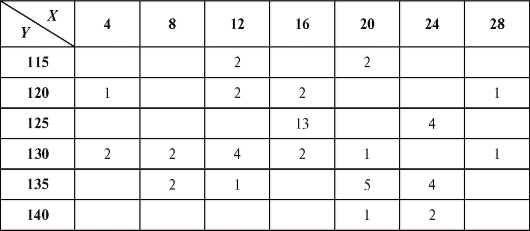
Таблица 8.33

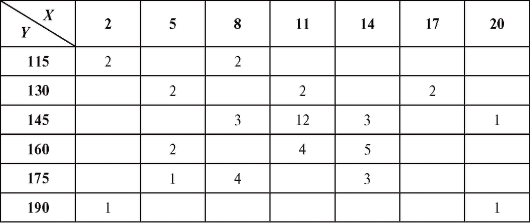
8.5. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ 8.5.1. Выбор из двух гипотез. Введение

В прикладных задачах часто требуется по наблюдениям выборки высказать некоторое суждение (гипотезу) относительно интересующих экспериментатора характеристик генеральной совокупности, из которой эта выборка извлечена.

В таких случаях говорят, что речь идет о проверке статистических гипотез.

Правила, согласно которым выясняется, соответствует ли интересующая нас гипотеза опытным данным, называются статистическими критериями или просто критериями.

Следует сказать, что статистические критерии - это, пожалуй, наиболее широко применяемые статистические средства. Они дают возможность экспериментатору найти разумный ответ на вопрос, подобный следующему.

В двух однородных группах больных гриппом, одной из которых проведена вакцинация средством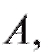а другой - средством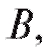среднее время выздоровления неодинаково. Указывает ли это обстоятельство на то, что одно противогриппозное средство по эффективности превосходит другое или же выявленное различие случайно?

Итак, пусть по наблюдениям выборки мы хотим подтвердить или опровергнуть некоторую гипотезу, скажем, о виде функции распределения случайной величины Х, которая является интересующей нас характеристикой генеральной совокупности. Такая гипотеза носит название нулевой гипотезы и обозначается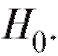

Наряду с гипотезой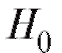необходимо также рассмотреть конкурирующую гипотезу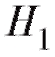, которая является альтернативной по отношению к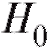, т. е. принимается в том случае, если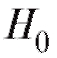не верна.

Например, если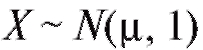, где параметр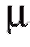предполагается неизвест-

ным, то в качестве нулевой гипотезы можно выбрать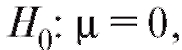а в каче-

стве конкурирующей гипотезы рассмотреть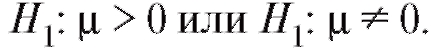

Пусть нам необходимо проверить справедливость гипотезы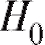при альтернативе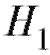(предполагая при этом, что либо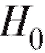, либо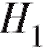имеет место). Поскольку выборочные наблюдения, на основе которых вопрос решается, являются случайными величинами, то абсолютно достоверно этого сделать нельзя. Всегда остается риск отвергнуть истинную гипотезу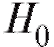, тем самым совершив так называемую ошибку первого рода (обозначается α), или же принять ложную гипотезу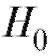, сделав ошибку второго рода (обозначается β) - табл. 8.34.

Таблица 8.34

Таким образом, любой критерий будет в той или иной мере субъективным, и нам следует по возможности минимизировать меру этой субъективности в принятии решения. Поступим следующим образом:

1. Зафиксируем некоторое малое положительное число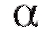(например,), называемое уровнем значимости.

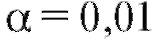
2. Выберем некоторую функцию Л, зависящую от выборки, которую будем называть статистикой критерия.

3. Среди всех возможных значений, принимаемых Л, определим множество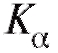(зависящее от вида статистики критерия Л и от уровня значимости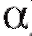), для которого вероятность события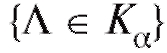, если верна гипотеза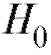, равна а, или

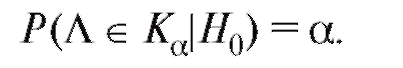(8.52)

Статистический критерий состоит в следующем: если статистика критерия Л, подсчитанная по выборке, попадает в множество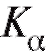 (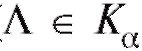), то гипотезаотвергается с вероятностью ошибки первого

рода, равной а (говорят, что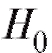отклоняется на уровне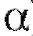), в противном случае (т. е. когда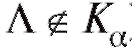), она принимается. В силу этого,называется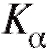

критической областью размера а.

Сконструированный таким способом критерий отвергает истинную гипотезу Н лишь в 100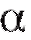случаях из 100 (при уровне значимости,

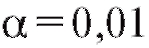например, лишь в одном случае из ста). Другими словами, попадание статистики критерия в критическую область дает нам веские основания считать, что нулевая гипотеза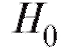не является истинной и справедлива конкурирующая гипотеза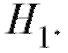

Соотношение, формально определяющее вероятность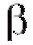ошибки второго рода (т. е. вероятность принять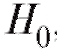, если верна гипотеза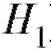), можно переписать в виде условия

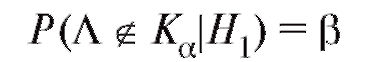(8.53) или

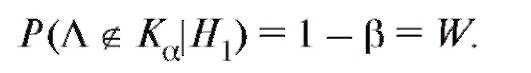(8.54)

Величина W называется мощностью критерия.

Замечание 1. Одновременное уменьшение ошибок первого и второго рода возможно лишь при увеличении объема выборки.

Таким образом, при заданной вероятности ошибки первого рода и фиксированном объеме выборки среди нескольких критериев лучшим является тот, у которого вероятность ошибки второго рода меньше (или мощность больше).

Отметим, что ошибки первого и второго рода имеют разный смысл. Так, применительно к судебной системе при гипотезе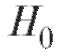«подсудимый виновен» ошибка первого рода приводит к оправданию виновного, а ошибка второго рода - к осуждению невинного.

Замечание 2. Согласно требованиям фармакопеи в биологических исследованиях принимается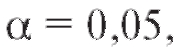а при разработке биологических

стандартов -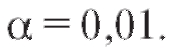

8.5.2. Проверка значимости коэффициента корреляции

Предположим, что интересующие нас характеристики X и Y объектов генеральной совокупности имеют двумерное нормальное распределение с неизвестным коэффициентом корреляции r. Требуется по наблюдениям выборки объема n, извлеченной из этой совокупности, проверить нулевую гипотезу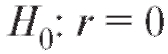при конкурирующей гипотезет. 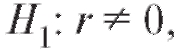е.

выяснить, будут ли случайные величины X и Y некоррелированными (и, следовательно, независимыми) или нет.

Обозначив через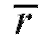 выборочный коэффициент корреляции (см.

(8.39)), возьмем в качестве статистики критерия функцию 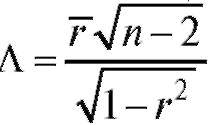и

положим 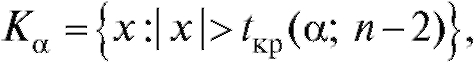где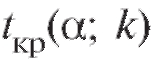- критическая точка

распределения Стьюдента, отвечающая уровню значимости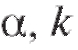степеням свободы и двусторонней критической области (см. приложение 2).

Известно, что при нулевой гипотезе случайная величина Л имеет распределение Стьюдента с n - 2 степенями свободы, и условие (8.52) выполняется. Можно также показать, что вероятность ошибки второго рода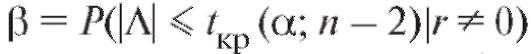стремится к нулю при.

Статистический критерий формулируется следующим образом. По извлеченным из генеральной совокупности наблюдениям выборки объема n следует вычислить выборочный коэффициент корреляции 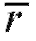и соответствующее ему наблюдаемое значение статистики критерия

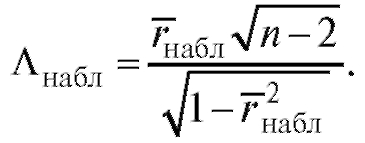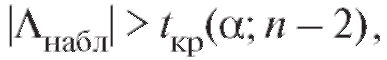Еслито нулевая гипотеза откло-

няется на уровне а, в противном случае, т. е. при,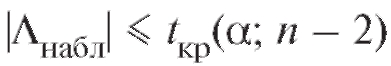

она принимается.

Пример. По данным примера 1, рассмотренного в п. 8.4.2, предполагая, что пара случайных величин X и Y имеет двумерное нормальное распределение при уровне значимости 0,01, проверить нулевую гипотезу о равенстве нулю коэффициента r корреляции u между X и Y при конкурирующей гипотезе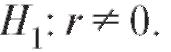

Решение. Найдем наблюдаемое значение статистики критерия

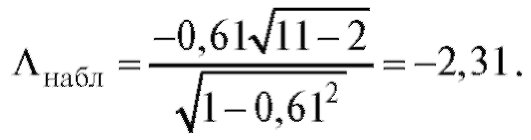В таблице критических точек распределения Стьюдента (см. приложение 2) по уровню значимости 0,01 и числу степеней свободы 11 - 2 = 9 находим критическую точку двусторонней критической области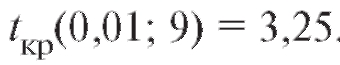Поскольку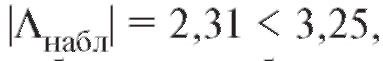

оснований отвергать нулевую гипотезу нет. Таким образом, выборочные данные не противоречат предположению о некоррелированности случайных величин X и Y.

8.5.3. Сравнение средних двух

нормально распределенных генеральных совокупностей

с неизвестными одинаковыми дисперсиями

Пусть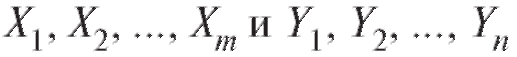- независимые выборки объема m

и n, извлеченные из генеральных совокупностей, нормально распределенных с неизвестными параметрами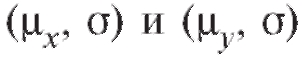соответственно. Обращаем внимание на то, что неизвестные генеральные дисперсии по предположению равны. Проверяется нулевая гипотеза о равенстве генеральных средних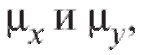т. е.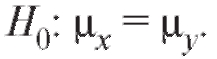

Сделаем следующее. Вычислим средние выборок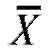и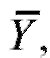а также их исправленные выборочные дисперси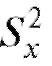и и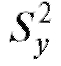 (см. формулы (8.7),

(8.8)). Затем образуем результирующую оценку общей дисперсии 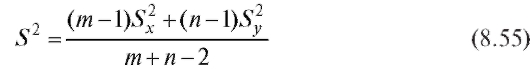и статистику критерия

При нулевой гипотезе статистика Л имеет распределение Стьюдента с m + n - 2 степенями свободы, что предопределяет дальнейший выбор критических областей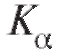при различных конкурирующих гипотезах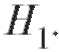

Сначала приведем статистический критерий проверки нулевой гипотезы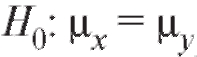при конкурирующей гипотезе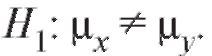

По формулам (8.55), (8.56) следует вычислить наблюдаемое значение статистики критерия Л_набл.

Если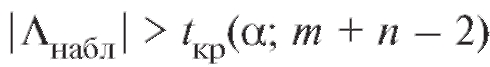, то нулевая гипотеза отклоняется на

уровне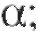если же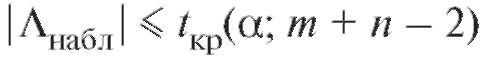- нулевая гипотеза прини-

мается.

Здесь величина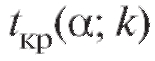так же, как в п. 8.5.2, определяется по табли-

це критических точек распределения Стьюдента (уровень значимости а, число степеней свободы к, двусторонняя область) из приложения 2.

Пример 1. Две группы детей, одинаковых по оценке умственных способностей, независимо обучались по двум различным методикам преподавания. Затем их подвергли выборочному тестированию, давшему следующие результаты:

1) объем выборки из первой группы равен 20,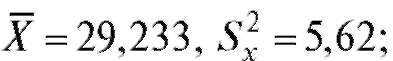

2) объем выборки из второй группы равен 10,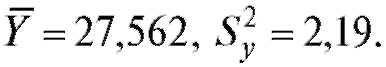 В предположении, что изучаемые показатели в каждой группе имеют

нормальное распределение с неизвестными средними и неизвестными, но одинаковыми дисперсиями, проверить при уровне значимости 0,05 существенно ли отличаются средние показания групп?

Решение. Проверяем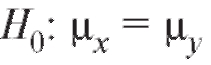при двусторонней альтернативе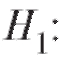

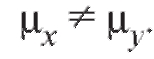Наблюдаемые значения статистики критерия

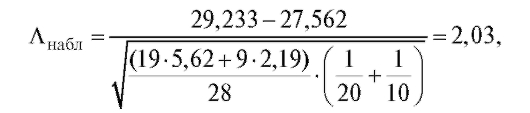
а критическая точка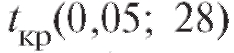распределения Стьюдента, соответ-

ствующая двусторонней области (см. приложение 2, верхняя строка), равна 2,05.

Поскольку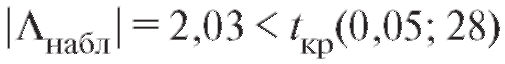, у нас нет оснований отвергать

нулевую гипотезу о равенстве средних в группах.

Далее сформулируем критерий проверки нулевой гипотезы :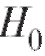

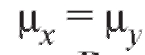при альтернативах 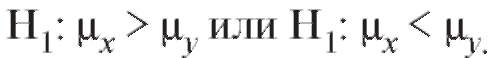В случае проверки нулевой гипотезы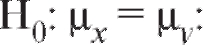

1) при конкурирующей гипотезе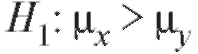нулевая гипотеза на уровне а отвергается, если

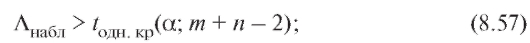
2) при конкурирующей гипотезенулевая гипотеза отвергается на уровне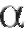, если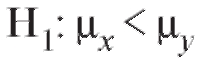

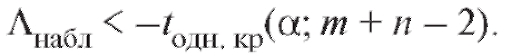
Здесь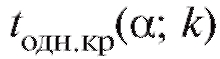- критическая точка распределения Стьюдента с

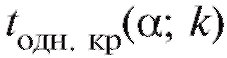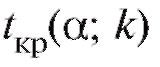уровнем значимости а, числом степеней свободы к, отвечающая правосторонней критической области (см. приложение 2, нижняя строка). Заметим, что критические точкиисвязаны соот-

ношением

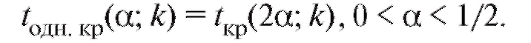
Например,.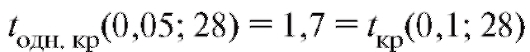

Пример 2. По данным примера 1 проверить при уровне значимости 0,05 нулевую гипотезу о равенстве среднихпри конкурирую-

щей гипотезе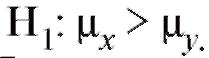

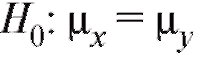
Решение. Поскольку наблюдаемое значение статистики,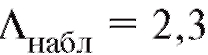

а соответствующее значение «односторонней» критической точки из приложения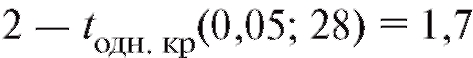, находим.

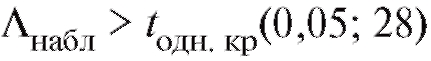Таким образом (см. (8.58)), статистика критерия попадает в критическую область и, следовательно, нулевая гипотеза отвергается в пользу предположения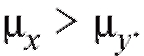Другими словами, выборочные данные значи-

мо отклоняются от нулевой гипотезы, и мы, в отличие от вывода примера 1, вынуждены заключить, что средние показания первой группы существенно превышают средние показания второй группы.

Отметим, что сравнение примеров 1 и 2 наглядно демонстрирует важность выбора конкурирующей гипотезы при проверке статистических гипотез.

8.5.4. Критерий равенства двух дисперсий

Пусть имеются две независимые выборки, первая - объемом m из наблюдений случайной величины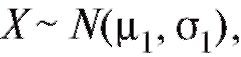и вторая - объемом n из

наблюдений случайной величины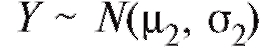. Требуется проверить,

согласуются ли выборочные данные с нулевой гипотезой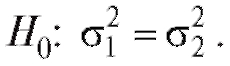

Заметим, что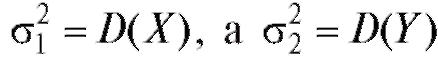, и, следовательно, нулевая ги-

потеза предполагает равенство генеральных дисперсий D(X) и D( Y), т. е.

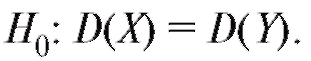
По выборкам, отвечающим случайным величинам Х и Y, вычислим исправленные выборочные дисперсии 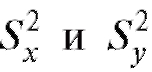и составим статистику

критерия

считая без потери общности, что

(в противном случае следует поменять обозначения Х и Y местами).

Можно доказать, что при нулевой гипотезе статистика критерия Л является случайной величиной, имеющей распределение Фишера-Снедекора (F-распределение) с m - 1 и n - 1 степенями свободы (напоминаем, что m - объем выборки, соответствующей числителю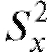дроби Л, в то время как n - объем выборки, определяющей знаменатель 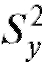этой дроби).

Для проверки на уровне значимости а нулевой гипотезы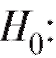 D(X) = D(Y) при конкурирующей гипотезе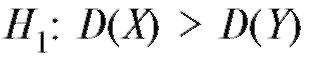следует по

выборочным данным с учетом договоренности (8.59) вычислить наблюдаемое значение статистики критерия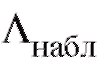и сравнить его с величиной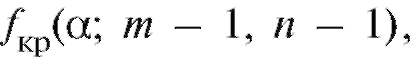которая является критической точкой F-распределения, отвечающей уровню значимости а и степеням свободы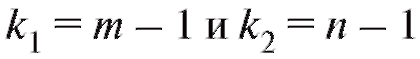. Значения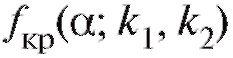при= 0,01, 0,05 и не 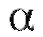которых к₁, к₂ содержатся в таблицах из приложения 3. Если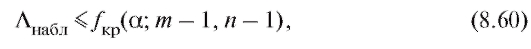

то нулевая гипотеза принимается; если же

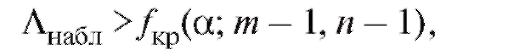
то нулевая гипотеза отклоняется на уровне а (и, следовательно, принимается конкурирующая гипотеза

В случае конкурирующей гипотезынулевая гипотеза

принимается, если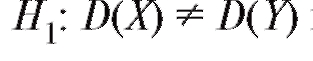

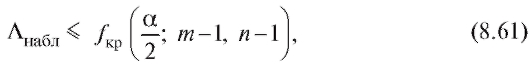
и отвергается на уровне а в противоположном случае.

Заметим, что вышеизложенная процедура проверки равенства дисперсий двух генеральных совокупностей чувствительна к нарушениям предположения о нормальности.

Пример. По данным примера 2, рассмотренного в п. 8.5.3, проверить предположение о равенстве дисперсий в тестируемых группах при И₁: 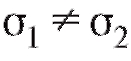и уровне значимости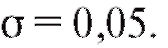

Решение. Имеем, 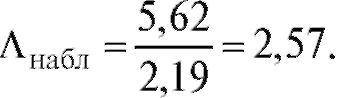Значения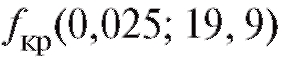в табли-

цах из приложения 3 нет, однако в силу того, что величина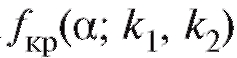 убывает с ростом.

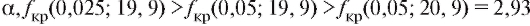Поскольку Л_набл = 2,57 < 2,93, условие (8.61) заведомо выполняется, откуда следует, что оснований отвергать предположение о равенстве дисперсий в тестируемых группах у нас нет.

8.5.5. Критерий согласия Пирсона (χ²-критерий)

Пусть интересующий нас признак генеральной совокупности является случайной величиной Х, и мы хотим по наблюдениям выборки из генеральной совокупности проверить некоторую гипотезу о функции распределения признака Х, ответив на вопрос: совместима ли эта гипотеза с выборочными данными? В такой ситуации говорят о проверке статистической гипотезы согласия.

Далее будет изложена одна довольно универсальная процедура, позволяющая по статистическому интервальному ряду распределения выборки (см. табл. 8.4) проверить гипотезу о том, что функция распределения признака Х генеральной совокупности совпадает с некоторой наперед данной функцией распределения Р(х). Эта процедура называется критерием согласия Пирсона или критерием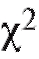(читается «хи квадрат критерий»).

Исходные данные для применения критерия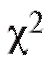представлены в табл. 8.4, содержащей информацию о том, сколько элементов n_i выборки объема n из наблюдений над случайной величиной Х попадает в интервалы группировки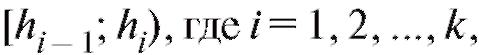причем 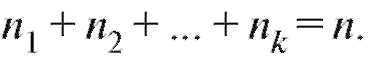Далее для удобства будем считать, что

Каждой наблюденной частотеставится в соответствие

ожидаемая теоретическая частота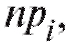где

(с учетом соглашения (8.62)), а Р(х) - предполагаемая (теоретическая) функция распределения, гипотеза о совпадении которой с функцией распределения случайной величины Х проверяется.

Понятно, что нужен способ объединения индивидуальных расхождений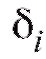из табл. 8.35 в некоторую общую статистику, которую можно было бы использовать как статистику критерия согласия при проверке нулевой гипотезы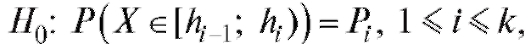при конкурирующей

гипотезе противоположной Н₀.

Таблица 8.35

Возьмем в качестве такой статистики величину

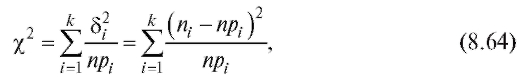
которая называется статистикой Пирсона или статистикой.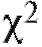

Можно показать, что при гипотезе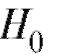статистика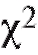, определяемая формулой (8.64), приближенно имеет распределение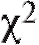с числом степеней свободы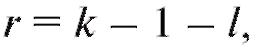где k - число интервалов группировки, а l - число неизвестных параметров теоретического распределения 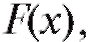определяемых по выборке.

Так, если предполагается, что распределение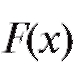является нормальным с параметрами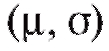и эти параметры известны, то l = 0 и r = k - 1; если же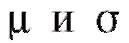заменяются их выборочными аналогами(см.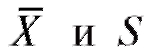

п. 8.2.1), то l = 2 и r = k - 3.

Критерий согласия Пирсона выглядит следующим образом. В таблице критических точек распределения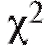(см. приложение 4) по заданному уровню значимости а и числу степеней свободы 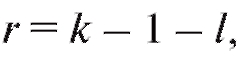где k - число интервалов группировки, l - число параметров теоретического распределения, определяемых по выборке, находят критическую точку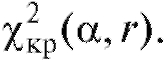Затем по формуле (8.64) (см. также (8.63) и

табл. 8.36) находят наблюдаемое значение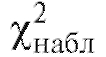статистики Пирсона.

Теперь, если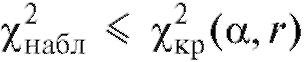, то оснований отвергнуть гипотезу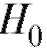

не имеется, и мы принимаем допущение, что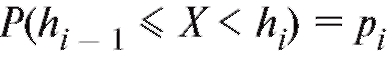при

всех

Если же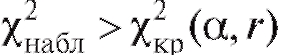, то гипотезу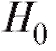отклоняют на уровне, при-

ближенно равном а, как несовместимую с выборочными данными.

Можно показать, что ошибка второго рода в критерии согласия Пирсона стремится к нулю при неограниченном возрастании объема выборки п.

Замечание 1. Справедлива формула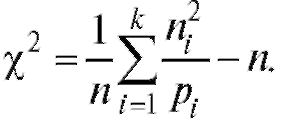

Замечание 2. Перед непосредственным применением критерия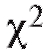 следует объединять интервалы (и складывать соответствующие частоты) группировки на «хвостах» таким образом, чтобы наименьшая ожидаемая частота была не меньше 1, т. е. если, например, в табл. 8.35 величина 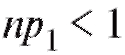, то интервалы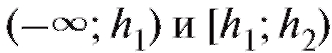объединяются в один общий ин-

тервал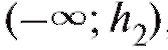, содержащий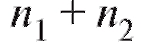наблюдений с ожидаемой частотой

.

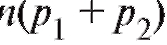Отметим, что в случае объединения интервалов число степеней свободы r статистики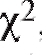, подсчитанной по преобразованной группировке, соответствующим образом уменьшится. Приведем два примера.

Пример 1. В препарате через равные промежутки времени регистрируется число бактерий, попавших в поле зрения микроскопа. Получены данные, представленные в табл. 8.36.

Таблица 8.36

Здесь i - число бактерий и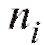- число моментов времени, соответствующих наблюдению ровно i бактерий.

Используя критерий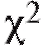, проверить при уровне значимости 0,05, что число бактерий, попадающих в поле зрения микроскопа в любой момент регистрации, распределено по закону Пуассона с параметром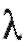= 1,5.

Решение. Будем считать, что признаком генеральной совокупности является неотрицательная случайная величина Х, равная числу бактерий, попадающих в поле зрения микроскопа в произвольный момент регистрации.

Тогда данные из табл. 8.36 представляют статистический ряд распределения выборки (см. табл. 8.1) объемом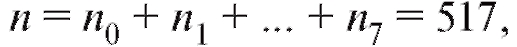отвечающей случайной величине Х. Разобьем ось на 8 интервалов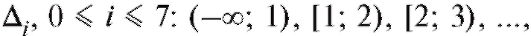

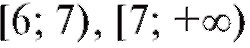. Тогда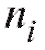означает число вариант, попавших в интервал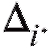

Учитывая, что случайная величина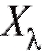, имеющая распределение Пуассона с параметром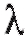, принимает лишь значения l = 0, 1, 2, ... с вероятностями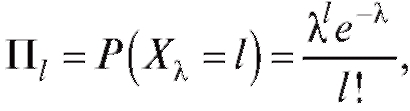заключаем, что теоретические вероятности

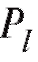(см. (8.64)) попадания соответствующего числа бактерий в поле зрения микроскопа с точностью до 10^-4, равны

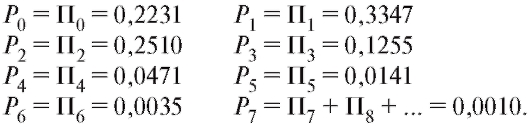
Таким образом, ожидаемые частоты равны 517 •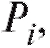и аналог табл. 8.35 представлен табл. 8.37.

Таблица 8.37

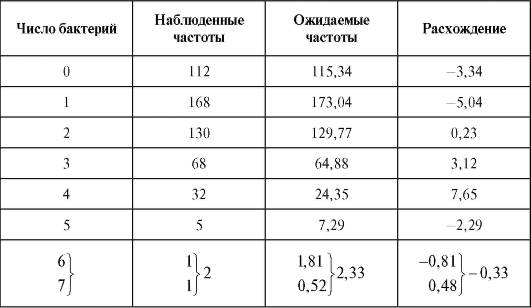
В соответствии с рекомендациями замечания 2 элементы двух последних строк табл. 8.37 должны быть объединены.

В результате число интервалов группировки с 8 уменьшается до 7, что приводит к уменьшению на единицу числа степеней свободы r

(с 7 = 8 - 1 до 6 = 7 - 1).

Критическая точка 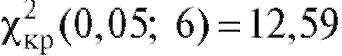(см. приложение 4), а наблю-

даемое значение статистики Пирсона, подсчитанное по формуле (8.65) (при k = 6 и с модифицированными частотами),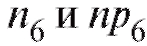

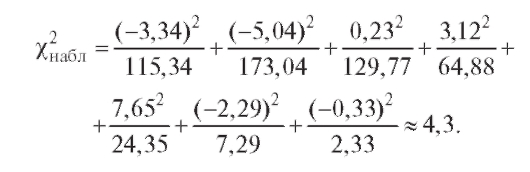
Поскольку 4,3 < 12,59, гипотеза о том, что число бактерий, попадающих в поле зрения микроскопа, распределено по закону Пуассона с параметром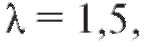принимается.

Пример 2. Проверить по критерию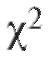при уровне значимости 0,05 гипотезу о том, что распределение признака Х из примера, рассмотренного в п. 8.1.4 (см. табл. 8.6), является нормальным с параметрами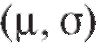, взяв в качестве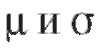их оценки, полученные по сгруппированным данным.

Решение. Оценки для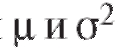найдем по формулам (8.11) и (8.12), взяв в них в качестве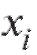середины интервалов группировки. Имеем,

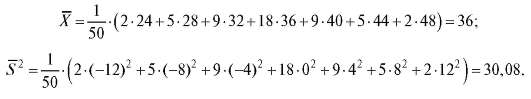
Принимая во внимание поправку Шеппарда на группировку, в соответствии с которой рекомендуется значение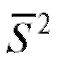уменьшать на где h - шаг группировки, окончательно получим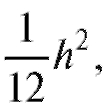

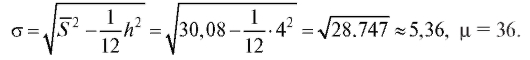
Составим табл. 8.38.

Таблица 8.38

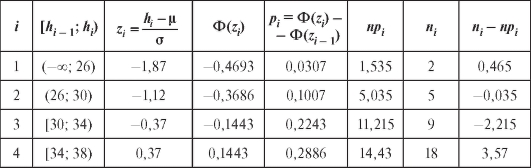
Окончание табл. 8.38

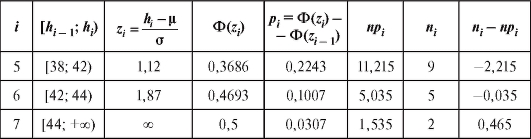
Здесь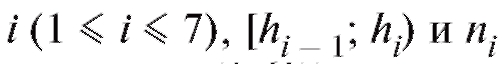- номер интервала группировки (с

учетом соглашения (8.62)),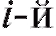интервал группировки и его частота соответственно;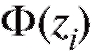вычисляется по приложению 1 (предполагается, что 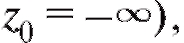а вероятности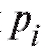- по формуле (8.63).

Вычислим наблюденное значение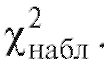 Имеем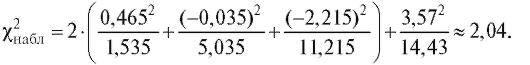

Учитывая, что критическая точка распределения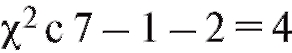сте-

пенями свободы и уровнем значимости 0,05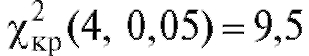превыша-

ет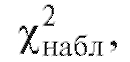делаем вывод о том, что гипотезане 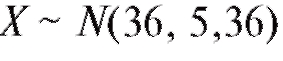противо-

речит статистическим данным.

Самостоятельная работа

1. По данным самостоятельных работ 1-4 из п. 8.4, предполагая, что пары наблюдаемых случайных величин X и Y имеют двумерное нормальное распределение, при уровнях значимости 0,05 и 0,01 проверить нулевую гипотезу о равенстве нулю коэффициента корреляции r между X и Y при конкурирующей гипотезе.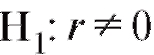

2. Средняя длина скорлупы 8 мелководных крабов оказалась равной 8,40 см при исправленной выборочной дисперсии этих длин 0,0016 см², а средняя длина скорлупы 12 глубоководных крабов оказалось равной 8,61 см при исправленной выборочной дисперсии этих длин 0,0038 см². Предполагается (с известной степенью точности), что обе выборки независимы и извлечены из нормально распределенных генеральных совокупностей. Определить, значимо или нет различаются между собой дисперсии длины скорлупы мелководных и глубоководных крабов при уровнях значимости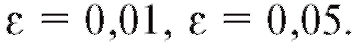Если различия между дисперсиями незначимы, проверить также гипотезу о равенстве генеральных средних.

3. Обследование 10 яиц, положенных кукушками в гнезда одного определенного вида птиц, показало, что средняя длина яйца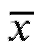= 21,9 мм, а S = 0,79 мм (здесь через S ² обозначена исправленная выборочная дисперсия). Обследование 15 яиц, положенных кукушками в гнезда другого определенного вида птиц, показало, что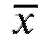= 22,6 мм, а S = 0,86 мм. Считается, что длина яйца распределена приближенно нормально. Определить значимость различий между дисперсиями длин яиц, положенных кукушками в гнезда разного вида птиц, и если различия между дисперсиями незначимы, проверить гипотезу о равенстве средних длин яиц. Уровни значимости принимаются ε = 0,01, ε = 0,05.

4. Даны результаты измерений частоты сердечных сокращений 11 студентов, проведенных сразу после окончания занятий по физкультуре, и 10 студентов - через полчаса после окончания этих занятий: исправленные выборочные дисперсии равны 139,9 и 74,2 соответственно. При уровнях значимости ε = 0,01, ε = 0,05 в предположении приближенной нормальности проверить гипотезу о равенстве генеральных дисперсий.

5. По группировкам, полученным в процессе решения самостоятельных работ 2-5 из п. 8.1, используя критерий х², проверить при уровнях значимости 0,05 и 0,01 гипотезу о нормальном распределении соответствующих признаков, взяв в качестве значений параметров нормального распределения их оценки, полученные по сгруппированным данным.

8.6. ВРЕМЕННЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ

Многие задачи науки и техники связаны с процессами, которые можно представить в виде совокупности измерений х_t на некотором интервале времени. Значение процесса х_t в каждый момент времени t является случайной величиной. Такие процессы называют временными рядами. Примерами временных рядов служат:

• запись электрокардиограммы;

• изменение уровня жидкости в капельнице;

• количество поступивших в медучреждение больных по дням;

• измерение артериального давления через каждый час.

Еще одним примером временного ряда может служить переменная х_t полученная при наложении случайных флуктуаций на детерми-

Рис. 8.9. Графическое изображение фрагмента временного ряда с параболическим трендом

нированную (неслучайную) составляющую (рис. 8.9), которую называют трендом временного ряда (тренд изображен на рис. 8.9 пунктирной линией).

В первых двух примерах измерения могут регистрироваться (по крайней мере, теоретически) непрерывно, в силу чего соответствующие временные ряды называют непрерывными, последние два примера относятся к группе дискретных временных рядов.

В дальнейшем мы будем рассматривать временные ряды лишь при целых значениях t, поскольку измерения обычно осуществляются через некоторые равные промежутки времени и нумеруются аналогично элементам выборки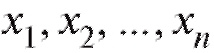объема n.

При изучении временных рядов основной интерес представляет моделирование их структуры с дальнейшим применением модели для экстраполяции или прогнозирования. При исследовании временных рядов необходим статистический подход из-за ошибок измерений и случайных флуктуаций, свойственных практически любой наблюдаемой системе, относится ли она к медицине, биологии, окружающей среде или технике. Важной составляющей статистических методов анализа временных рядов является оценка тренда, который, при наличии информации об его виде, можно моделировать при помощи компонент, являющихся детерминированными функциями времени. Отметим, что эксперименты, в которых осуществляются наблюдения, как правило, не являются независимыми, и последовательные ошибки модели должны, вообще говоря, рассматриваться как статистически связанные. Обычной практикой является предположение, что последовательные ошибки модели представляют стационарный временной ряд.

Определение. Временной ряд х_t называют стационарным, если:

1) математическое ожидание и дисперсия ряда постоянны во времени:

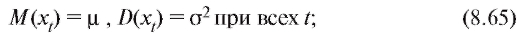
2) ковариация между любыми членами ряда (см. п. 7.2.4) зависит только от расстояния во времени между этими наблюдениями или (в дискретном случае) от разности между их номерами, т. е. 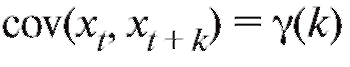для всех t зависит лишь от k.

Заметим, что если совместное распределение членов стационарного временного ряда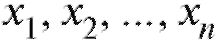при любом п является нормальным, то со-

вместное распределение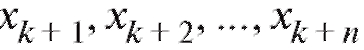не зависит от k, или, други-

ми словами, вероятностное поведение любой группы членов временного ряда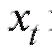не зависит от сдвига по t. В частности любые индивидуальные вероятностные характеристики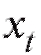не изменяются во времени.

8.6.1. Оценки вероятностных характеристик временных рядов

Пусть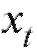является стационарным временным рядом, и мы хотим оценить его параметры (см. формулу (8.65)) по наблюдениям (выборке) х₁, 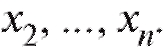Можно показать, что при некоторых весьма слабых предположениях несмещенной и состоятельной оценкой (см. п. 8.2.1) для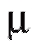является выборочное среднее

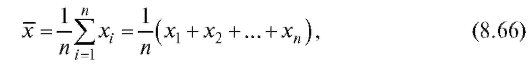
а состоятельной оценкой для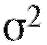будет выборочная дисперсия S², которую можно определить как среднее арифметическое квадратов отклонений наблюдавшихся значений временного ряда от их среднего значения:

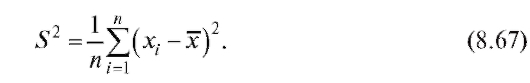
Заметим, что формулы (8.66) и (8.67) совпадают с формулами (8.7), (8.8), что неудивительно, поскольку и те, и другие оценивают одни и те же вероятностные характеристики.

Моделью некоторых нестационарных временных рядов служат процессы вида

где детерминированная функция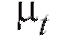зависит лишь от t, а х_t - стационарный временной ряд с нулевым средним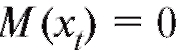. Очевидно, что

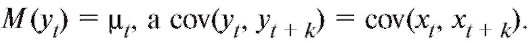Поэтому детерминированная компонента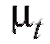характеризует тенденцию изменения в среднем временного ряда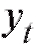со временем, т. е. его тренд, а слагаемое х_t определяет случайные, не зависящие от t, ошибки модели и структуру их зависимости. Типичный вид графического изображения подобного нестационарного временного ряда был изображен на рис. 8.9.

8.6.2. Сглаживание временных рядов

Как уже говорилось ранее, одной из задач теории временных рядов является оценивание тренда временного ряда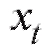по результатам наблюдений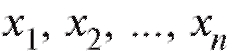его отрезка длины п. Эту процедуру можно осуществить при помощи операции сглаживания, целью которой является уменьшение дисперсии временного ряда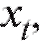а, по существу, амплитуды случайных флуктуаций вокруг его детерминированной составляющей. Сглаженный временной ряд обычно получают, как линейную комбинацию элементовс некоторыми неотрицательными весами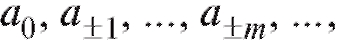в сумме равными единице, которые желательно выбирать, используя информацию о ковариационной структуре ряда. На практике в основном ограничиваются методом экспоненциального сглаживания или его частным случаем - методом скользящего среднего. При любом использованном методе сглаживания исследователь рассчитывает, что полученный в результате сглаживания новый временной ряд 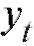будет иметь более четко выраженный тренд, мало отличающийся от тренда первоначального ряда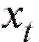и, следовательно, в первом приближении могущий его заменить.

Приведем формулу для метода экспоненциального сглаживания по трем точкам:

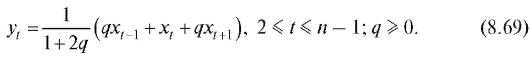
Если в (8.69) положить q = 1, получим формулу для метода скользящего среднего по трем точкам:

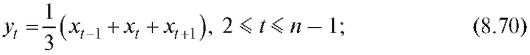
устремляя q к бесконечности, придем к сглаживающей формуле

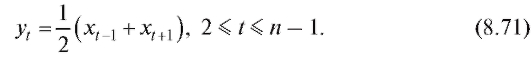
Соотношения (8.69) и (8.70) легко обобщаются с трех на произвольное нечетное число точек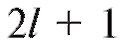. Соответствующий вариант формулы (8.71), например, имеет вид

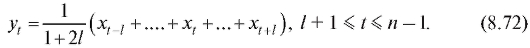
Приведенные методы сглаживания оставляют линейный тренд временного ряда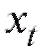без изменения и, вообще говоря, уменьшают его дис-

персию. Отметим также, что при сглаживании, как правило, происходит некоторая потеря информации. Так, при использовании метода скользящего среднего по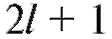точкам отрезок сглаженного ряда будет содержать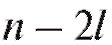элементов вместо п.

Отметим также, что при сглаживании, как правило, происходит некоторая потеря информации. Так, при использовании метода скользящего среднего по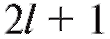точкам отрезок сглаженного ряда будет содержать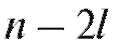элементов вместо п.

Пример 1. Данные о динамике роста объема производства х_t некоторого препарата (в тоннах) на фармацевтической фабрике за 10 последовательных лет представлены в табл. 8.39. Провести сглаживание временного ряда х_t используя формулы (8.70), (8.71) и (8.69) при q = 3/4. На одном графике построить изображение ряда х_t и трех сглаженных его вариантов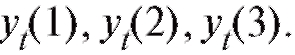

Таблица 8.39

Решение. Сглаженные значения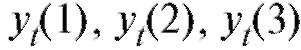, подсчитанные при

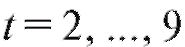по указанным формулам, запишем в табл. 8.40.

Таблица 8.40

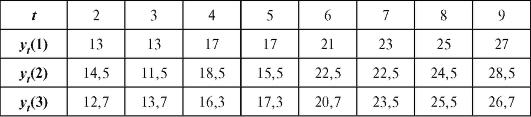
Например, столбцы таблицы, соответствующие t = 2 и t = 9, заполняются следующим образом:

y₂(1) = (12 + 10 + 17)/3 = 13, y₂(2) = (12 + 17)/2 = 14,5; y₂(3) = (12.3 + 10.4 + 17.3)/10 = 12,7; y₉(1) = (27 + 24 + 30)/3 = 27, y₉(2) = (27 + 30)/2 = 28,5; y₉(3) = (27.3 + 24.4 + 30.3)/10 = 26,7.

Графики, построенные по табл. 8.39 и 8.40, изображены на рис. 8.10. Их визуальный анализ дает основания полагать, что наблюдаемый временной ряд имеет линейный тренд.

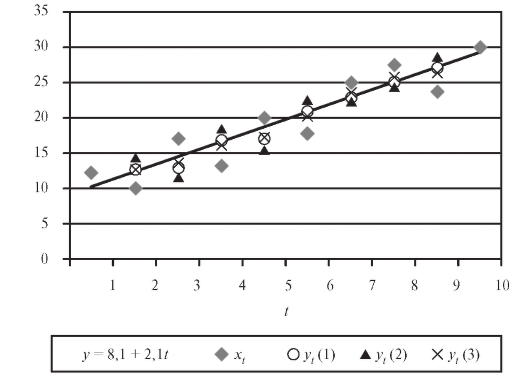
Рис. 8.10. Графики, построенные по табл. 8.39 и 8.40

Если с помощью, скажем, метода скользящего среднего или из каких-либо других, например теоретических, соображений сделан вывод, что тренд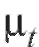временного ряда (см. (8.68)) является функцией, известной с точностью до нескольких параметров, то оценки последних можно определить, используя метод наименьших квадратов.

В случае, когда трендявляется линейной функцией времени, т. е. 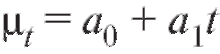, МНК-оценки параметров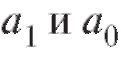выражаются формулами

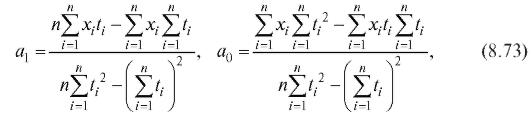
в которых х_i является значением временного ряда в момент времени

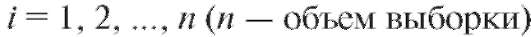. Обращаем внимание на то, что формулы (8.73) с точностью до обозначений совпадают с формулами (8.32) и (8.33).

Пример 2. По данным табл. 8.39 методом наименьших квадратов оценить коэффициенты уравнения линейного тренда для зависимости объема производства от номера года.

Решение. Для оценки параметров уравнения трендапри-

меним формулы (8.74):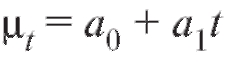

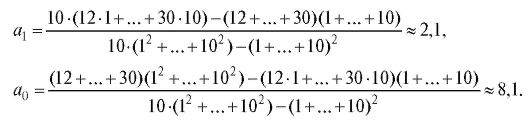
Таким образом, уравнение тренда имеет вид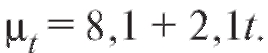

В заключение заметим, что знание тренда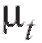временного ряда позволяет с известной степенью надежности и точности прогнозировать его значения. Предположительные значения ряда для моментов времени t, выходящих за границу проведенных наблюдений, считаются равными 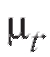При этом важно понимать, что оценки подобного рода предполагают то, что основная тенденция изменения временного ряда в течение интервала времени между моментом наблюдения и моментом времени, для которого оценивается значение временного ряда, сохраняется. Кроме того, надо иметь в виду, что точность прогноза, как правило, снижается с ростом этого интервала.

Пример 3. Используя результат решения примера 2, оценить объем производства указанного препарата (в тоннах) на фармацевтической фабрике в 11-м году от начала наблюдений.

Решение. Уравнение тренда для зависимости объема производства от номера года наблюдений из примера 2 имеет вид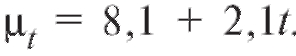 Подставляя в это уравнение значение t = 11, получим прогнозируемое на 11-й год от начала наблюдений значение объема производства

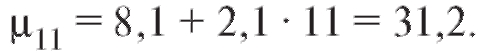
Самостоятельная работа

1. В табл. 8.41 приведены данные об объемах реализации некоторого препарата (в тысяче упаковок) в аптеке за 9 последовательных месяцев. В предположении стационарности временного ряда, образуемого этими значениями, оценить математическое ожидание, дисперсию и среднее квадратичное отклонение для этого ряда.

Таблица 8.41

2. В табл. 8.42 приведены результаты измерения массы лабораторного животного (в граммах), полученные последовательно в течение 12 дней. В предположении стационарности временного ряда, образуемого этими значениями, оценить математическое ожидание, дисперсию и среднее квадратичное отклонение для этого ряда.

Таблица 8.42

3. Данные по дисциплине роста товарооборота аптеки (в десятках миллионов рублей) за 10 последовательных лет представлены в табл. 8.43. Составить уравнение тренда для зависимости товарооборота аптеки от года в предположении линейности этой зависимости и оценить товарооборот аптеки в 11-м году от начала наблюдений.

Таблица 8.43

4. Методом скользящего среднего по трем точкам произвести сглаживание временного ряда из задания 3.