Глава 7. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Теория вероятностей как научная дисциплина занимается изучением закономерностей в случайных явлениях. Она изучает модели экспериментов, результат которых нельзя предсказать определенно. Погода на завтрашний день, доля отбракованных деталей при их массовом производстве, прогнозирование курса акций при устойчивом финансовом положении рынка и т. п. - все это предмет приложений теории вероятностей.

7.1. СЛУЧАЙНЫЕ СОБЫТИЯ И ИХ ВЕРОЯТНОСТИ 7.1.1. Элементы комбинаторики

Комбинаторика - это раздел математики, изучающий вопросы о том, сколько комбинаций определенного типа можно составить из данных элементов.

Теорема 7.1 (о числе комбинаций). Пусть имеется m множеств по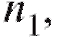

элементов в каждом. Выбрать по одному объекту из каждого множества можноспособами.

Пример 1. Из трех классов спортивной школы надо составить команду по одному ученику от класса. Сколько различных команд можно составить, если в классах 18, 20 и 22 ученика соответственно.

Решение. Ответ на вопрос этого примера вытекает из теоремы 7.1 при m = 3, n₁ = 18, n₂ = 20, n₃ = 22. Всего можно составить 18 • 20 • 22 = 7920 команд.

Определение. Множество из n элементов называется упорядоченным, если каждому его элементу поставлен в соответствие свой номер от 1 до n.

Если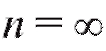, то множество называется счетньм. Определение. Упорядоченные наборы, составленные из всех элементов данного конечного множества, называются перестановками этого множества.

Пример 2. Множество из трех элементов {1, 2, 3} имеет следующие перестановки (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). Всего их шесть.

Теорема 7.2 (о числе перестановок). Число всех перестановок множества из n элементов определяется формулой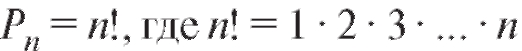 (считаем, что по определению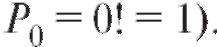

Пример 3. Цифры 0, 1, 2, 3 записаны на 4-х карточках. Сколько различных 4-значных цифр можно составить из этих карточек?

Решение. Число различных комбинаций из 4-х цифр равно 4!; 3! комбинаций, начинающихся с 0, следует исключить. В результате количество различных 4-значных чисел равно 4! - 3! = 18.

Определение. Упорядоченные наборы, состоящие из k элементов, взятых из данных n элементов, называются размещениями из n элементов по k.

Размещения отличаются друг от друга либо элементами, либо порядком.

Теорема 7.3 (о числе размещений). Число всех размещений из n элементов по k определяется формулой

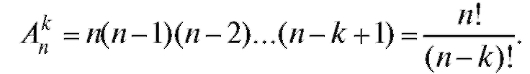
Например, из множества {1, 2, 3} по два элемента можно (с учетом порядка) выбрать 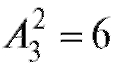способами: (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),

(3, 2).

При k = n из теоремы 7.3 следует теорема 7.2, т. е.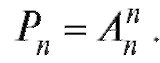 Пример 4. Сколько имеется вариантов занятия трех призовых мест 8-ю спортсменами одного уровня?

Решение. Ответ дается формулой .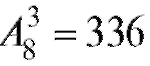

Определение. Неупорядоченные наборы, состоящие из k элементов, взятых из данных n элементов, называются сочетаниями из n элементов по k.

Сочетания отличаются друг от друга лишь элементами.

Так, для множества {1, 2, 3} сочетаниями по два элемента являются комбинации (1, 2), (1, 3), (2, 3).

Теорема 7.4 (о числе сочетаний). Число всех сочетаний из n элементов по k определяется формулой

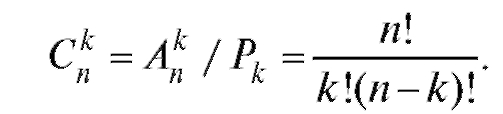
Коэффициенты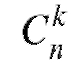 называют биномиальными коэффициентами, так как они входят в формулу бинома Ньютона:

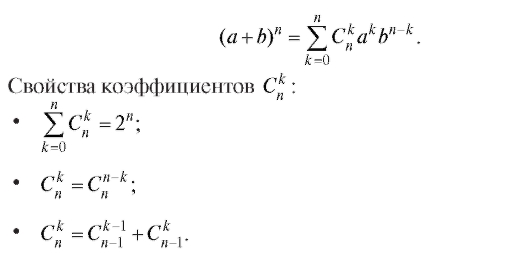
Пример 5. В турнире участвует 6 команд. Каждая команда должна сыграть с каждой одну игру. Сколько игр сыграно в турнире?

Решение. Различные пары команд образуют сочетания из 6 по 2, поскольку порядок среди двух команд, играющих в одной игре, нам безразличен. Следовательно, число игр будет равно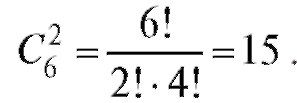

Пример 6. Сколькими способами можно выбрать 2 ампулы из упаковки, содержащей 10 ампул.

Решение. По аналогии с предыдущим примером

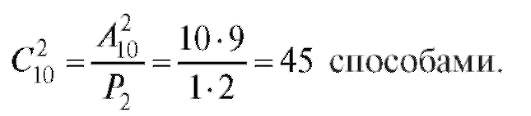
Пример 7. У 6 мальчиков и 11 девочек имеются признаки инфекционного заболевания. Чтобы проверить наличие заболевания, требуется взять выборочный анализ крови у 2 мальчиков и 2 девочек. Сколькими способами можно это сделать?

Решение. Количество способов выбора двух мальчиков:

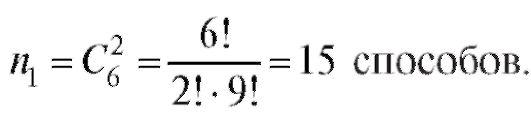
Количество способов выбора двух девочек:

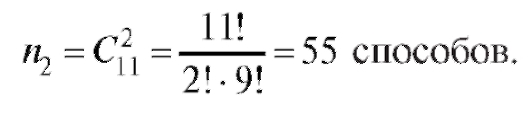
Поскольку каждая пара мальчиков может быть взята с каждой парой девочек, то по теореме 7.1 имеем:

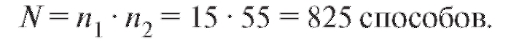
7.1.2. Случайные события и их свойства

В основе теории вероятностей лежит понятие случайного эксперимента, т. е. эксперимента, который может закончиться любым из некоторого множества известных результатов, но заранее (до осуществления эксперимента) неизвестно каким.

Так, бросая игральную кость, нельзя быть заранее уверенным, что выпадает грань с номером 6.

В дальнейшем исходами будем называть различные результаты эксперимента.

Определение. Пространством элементарных исходов называется множество всех взаимно исключающих (т. е. не могущих наступить одновременно) исходов эксперимента.

Пространство элементарных исходов мы будем обозначать буквой Определение. Событием называется любое подмножество Событие может состоять из одного или нескольких исходов, а может включать счетное или даже несчетное число исходов. События будут обозначаться прописными буквами А, В, ... или же словами.

Будем говорить, что событие А наступило, если эксперимент заканчивается одним из исходов, входящих в событие А. Пример 1. Бросание игральной кости.

Здесь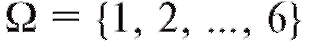состоит из шести исходов, заключающихся в

выпадении грани с соответствующим номером. Событие А = {выпало четное число} состоит из трех исходов, т. е. А = {2, 4, 6}. Считаем, что А наступило, если при бросании игральной кости выпала грань с номером 2, 4 или 6.

Пример 2. Стрельба по мишени до первого попадания. Здесь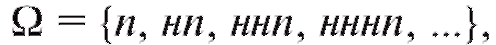где исход п = {попадание при первом

выстреле}, а исход н...нп, где «н встречается k» раз означает, что стрелок первые k раз промахнулся, а в (k + 1)-й раз мишень была поражена. В данном случае пространство элементарныхсчет-

ным множеством.

Заметим, возвращаясь несколько назад, что выборсубъективен и диктуется условиями задачи, а, следовательно, может быть разным в одном и том же эксперименте.

Так, если в условиях примера 1 нас интересует лишь четное или нечетное число очков выпало, то логично в качестве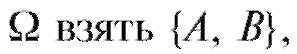где А = {2, 4, 6}, В = {1, 3, 5}.

Определение.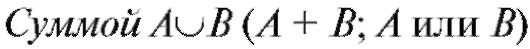называют событие, состо-

ящее из всех исходов, принадлежащих либо А, либо В.

Определение. Произведением АВ двух событий А и В называют событие, состоящее только из тех исходов, которые входят в А и В одновременно.

Определение. Разностью А - В двух событий А и В называется событие, состоящее из исходов, входящих в А, но не входящих в В.

Если события изобразить множествами на плоскости, то результат определенных операций над событиями выглядит так, как представлено на рис. 7.1-7.3.

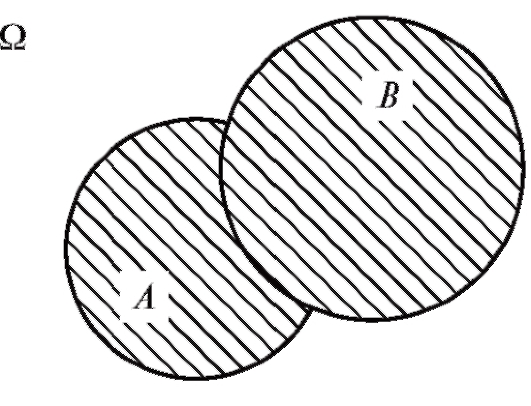
Рис. 7.1. Сумма событий А + В

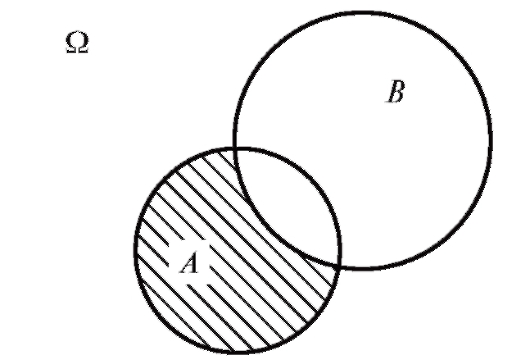
Рис. 7.2. Разность событий А - В

Пример 3. Пусть при бросании игральной кости (см. пример 1) событие А = {1, 3, 5} = {выпало нечетное число очков}, а событие В = {3, 6} = {выпало число очков, кратное трем}. Тогда А + В = {1, 3, 5, 6}, АВ = {3}, А - В = {1, 5}, В - А = {6}.

Определение. Противоположным (дополнительным) для события А называется событие 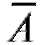, состоящее из всех исходов, не входящих в А (рис. 7.4). Отметим, что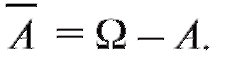

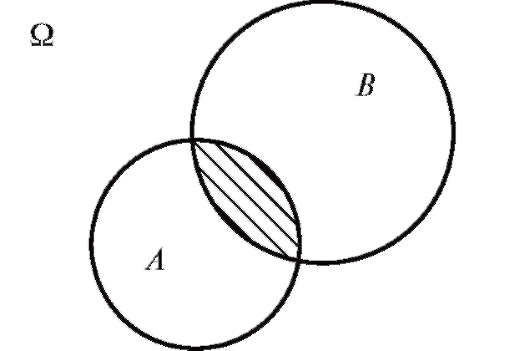
Рис. 7.3. Произведение событий АВ

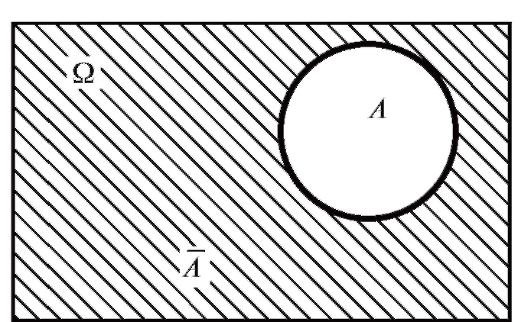
Рис. 7.4. События A и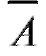

Пример 4. Противоположными событиям А и В из примера 2 являются события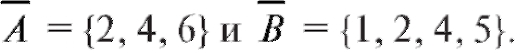

Определение. Событиеназывается достоверным (оно обязательно происходит). Событие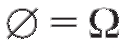называется невозможным.

Примером невозможного события при бросании игральной кости на ровную поверхность является событие, заключающееся в том, что игральная кость встала на вершину.

Определение. События А и В называются несовместными, если они не могут наступать одновременно.

Примером несовместных событий служат события А - В и В. Отметим, что если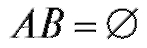, то события А и В обязательно несовместны.

Определение. Говорят, что событие А содержится в событии,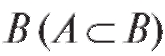

если все исходы события А входят в событие В. Так,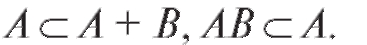

Приведем некоторые свойства операций над событиями:

Следует иметь в виду, что событие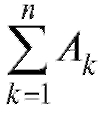наступает, если происходит

«хотя бы одно» событие из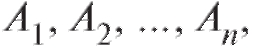а наступление события

означает, что ни одно событие из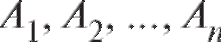не произошло.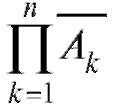

При бросании игральной кости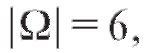а вероятности выпадения лю-

бой грани одинаковы и равны 1/6;

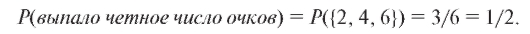
Пример 2. Какова вероятность угадать в лотерее 6 чисел из 49? Решение. Здесьравно совокупности всех сочетаний из 49 чисел по

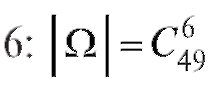. Благоприятствует выигрышу лишь одно событие. Поэтому

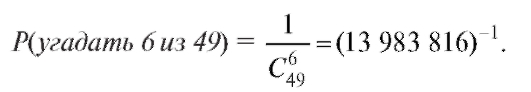
Пример 3. В клетке имеется 10 мышей: 3 белых и 7 серых. Наудачу вытаскивается одна мышь. Какова вероятность события А, что эта мышь белая.

Решение. В этом примере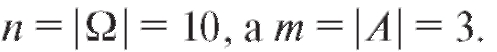В соответствии с

формулой (7.3) вероятность вытащить белую мышь равна 3/10.

Замечание. Слово «наудачу», употребленное в примере 3, является синонимом выражения «случайным образом» и означает выбор, при котором все комбинации элементов, которые могут быть выбраны, равновозможны.

Пример 4. Технический контроль из партии в 10 изделий проверяет взятые наудачу 3 изделия. Партия не принимается, если среди трех проверяемых изделий окажется хотя бы одно бракованное. Определить вероятность приемки партии, если в ней окажется 5 бракованных изделий.

Решение. Обозначим через А событие, состоящее в том, что партия изделий будет принята. Общее число исходов, состоящее в проверке

трех наудачу взятых изделий из 10, равно 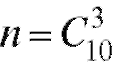, т. е. числу сочетаний

из 10 по 3. Событию А благоприятствуют 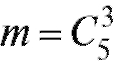исходов. Таким обра-

зом, получаем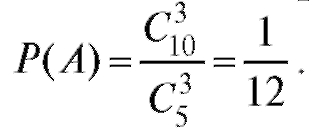

Пример 5. При наборе телефонного номера абонент забыл две последние цифры и наудачу набрал их, помня только, что эти цифры нечетные и различные. Найти вероятность того, что номер набран правильно.

Решение. В этой задаче порядок набора цифр важен. Поэтому для определения числа всех возможных исходов следует использовать теорему 7.3 о числе размещений. Количество благоприятных исходов здесь равно 1, так как правильным является только один номер. Следовательно, искомая вероятность равна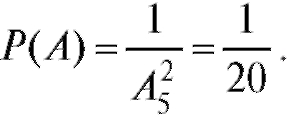

Пример 6. Пусть в группе из 10 человек четверо мужчин. Если случайным образом выбирают двух человек, то какова вероятность, что это: а) оба мужчины; б) обе женщины; в) один мужчина и одна женщина?

Решение. Обозначим события:

• А - выбирают двух мужчин;

• В - выбирают двух женщин;

• С - выбирают одного мужчину и одну женщину. Число всех исходов

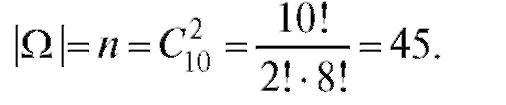
Число выбора двух мужчин из четырех и двух женщин из шести: 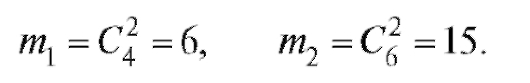По формуле (7.3) имеем

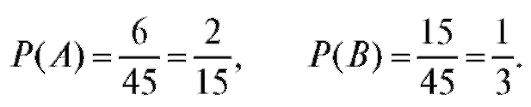
Наконец, существует 4 способа выбора одного мужчины и 6 способов выбора одной женщины. По теореме 7.1 о числе комбинаций количество способов выбора двух человек обоего пола равно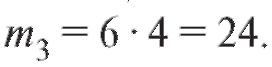Таким образом,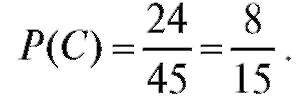

Пример 7. Из 20 человек, одновременно заболевших гриппом, 15 выздоровели полностью за 3 дня. Предположим, что из этих 20 человек случайным образом выбирают 5. Какова вероятность того, что за 3 дня из этих человек выздоравливают: а) 5 человек; б) 4 человека; в) никто не выздоравливает?

Решение. Определим события:

• А - за 3 дня выздоравливают 5 человек;

• В - за 3 дня выздоравливают 4 человека;

• С - за 3 дня не выздоравливает никто.

Число всех исходов равно.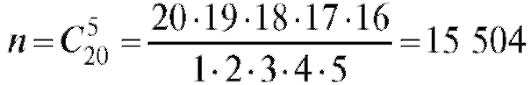

Число способов выбора из 15 выздоровевших пяти человек -

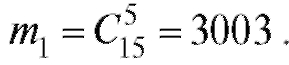Таким образом, .

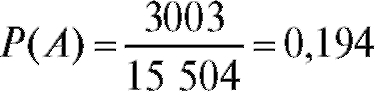Число способов выбора из 15 выздоровевших четырех человек - 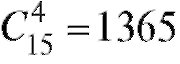, одного невыздоровевшего из пяти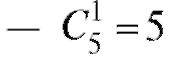. По теореме 7.1

число способов выбора 5 человек, из которых выздоравливают за 3 дня только четверо, равно 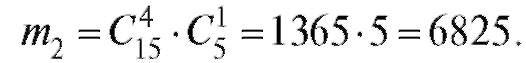Следовательно

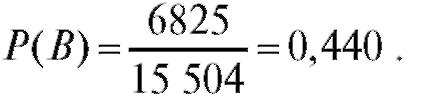
Число способов выбора пяти невыздоровевших из пяти человек равно 1, откуда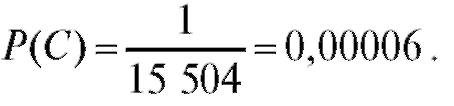

Пример 8. На полке 6 книг по математике и 4 по физике. Найти вероятность того, что среди выбранных наудачу пяти книг будут три по математике и две по физике.

Решение. Три книги по математике можно выбрать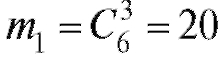спо-

собами, а две книги по физике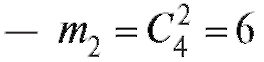способами.

Пять книг, среди которых три по математике и две по физике, по теореме о числе комбинаций можно выбрать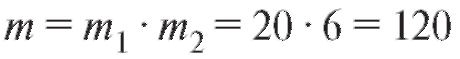способами.

Число всех исходов равно 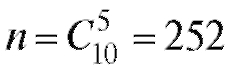. Искомая вероятность по

формуле (7.3) равна.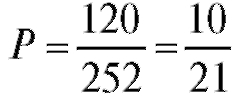

Пример 9. В клетке 6 белых и 4 серых мыши. Случайным образом извлекают 3 мыши. Вычислить вероятность для 4 возможных комбинаций цвета мышей.

Решение. Обозначим:

• б - белая мышь;

• с - серая мышь;

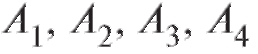• - события, состоящие в появлении одной из возможных комбинаций цвета мышей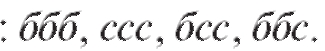

Число всех исходов равно(всего мышей 10, вы-

бираем 3).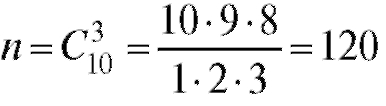

Число способов выбора из шести белых мышей трех равно 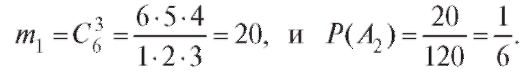Число способов выбора из четырех серых мышей трех равно

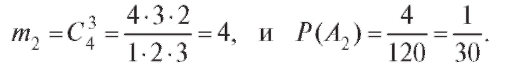
Событие A₃ состоит в том, что из шести белых мышей нужно выбрать одну - это 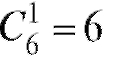способов, и из четырех серых мышей выбрать две -

это 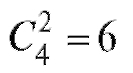способов. Общее количество вариантов будет равно

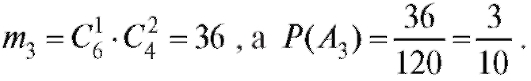
Рассуждая аналогично, найдем общее число способов выбора двух белых и одной серой мыши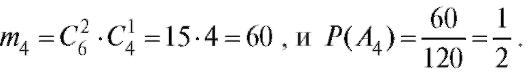

Пример 10. В коробке 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди отобранных изделий: а) одно окрашено; б) два окрашены; в) хотя бы одно окрашено.

Решение. Обозначим события:

• А - окрашено одно изделие из двух извлеченных;

• В - окрашены два;

• С - оба не окрашены.

Число всех исходов определяется как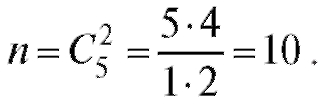

Так как окрашено одно изделие, то второе не окрашено и, следовательно,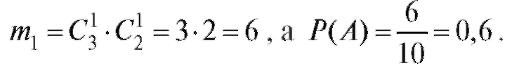

Поскольку из двух извлеченных изделий окрашены два, то неокрашенных нет вовсе и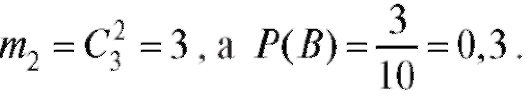

Здесь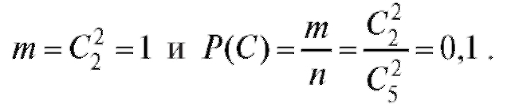

Пример 11. Из пяти карточек с буквами А, Б, В, Г, Д наугад выбираются три и располагаются в ряд в порядке появления. Какова вероятность того, что получится слово «два»?

Решение. Так как положение буквы в комбинации имеет значение, то для определения общего числа возможных исходов следует пользоваться размещениями: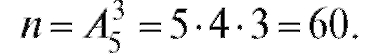

Здесь m = 1, так как требуется получить только одно слово «два». Следовательно,.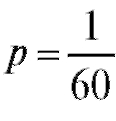

7.1.4. Свойства вероятностей

Свойство 1.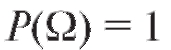в силу условия нормировки (7.1).

Свойство 2.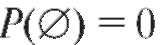, так как в (7.2) сумма не содержит слагаемых.

Свойство 3. Если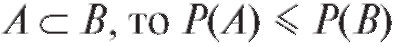(в сумме (7.2), определяющей

Р(В), присутствуют дополнительные по сравнению с Р(А) неотрицательные слагаемые). Свойство 4. 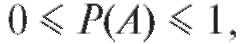что следует из свойств 3 и 1.

Свойство 5. 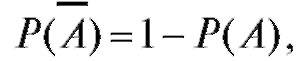так как по свойству 1

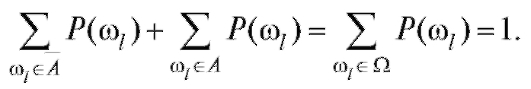
Свойство 5 важно в практическом отношении, так как позволяет вычислить вероятность события А, если известна вероятность противоположного события A.

Пример 1. Из полного набора костей домино наугад берутся пять костей. Найти вероятность того, что среди них будет хотя бы одна с шестеркой.

Решение. При решении этой задачи удобно использовать свойство 5 вероятностей, перейдя к противоположному событию «среди пяти отобранных костей домино нет ни одной шестерки».

Число всех исходов

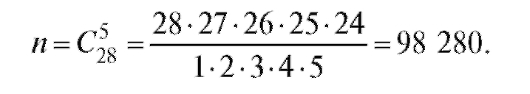
Поскольку количество костей домино, не содержащих шестерку, равно 21, то число исходов, благоприятствующих противоположному событию, будет:

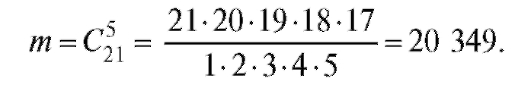
Отсюда (см. (7.3))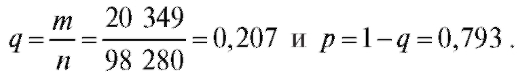

Из свойства 5 вероятностей и свойства 15 операций над событиями вытекает следующее соотношение: для любого набора событий,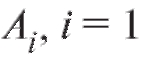

2, ... , n,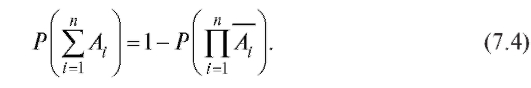

Равенство (7.4) означает, что вероятность того, что произошло «хотя бы одно» событие из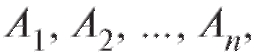можно найти, вычитая из 1 вероят-

ность того, что не произошло ни одно событие из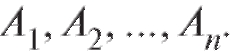В некото-

рых случаях таким приемом удобно пользоваться.

Свойство 6. Для любых событий А и В имеет место формула сложения вероятностей

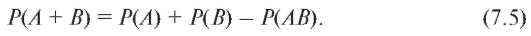
При проверке равенства (7.5) полезно воспользоваться геометрической иллюстрацией событий А + В и АВ (см. рис. 7.1 и 7.2), интерпретируя вероятности событий как площади соответствующих им изображений.

Пример 2. В марте 7 дней шел снег, 10 дней - дождь, из них 4 дня - снег с дождем. Найти вероятность того, что в выбранный наугад день шел дождь или снег.

Решение. Пусть А = {шел снег} и В = {шел дождь}. По формуле (7.5)

Р(шел дождь или снег) =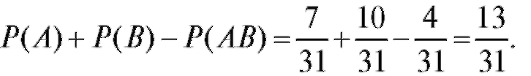

Пример 3. Из 100 студентов, находящихся в аудитории, 50 человек знают английский язык, 40 - французский, 35 - немецкий. Английский и французский знают 20 человек, английский и немецкий - 8, французский и немецкий - 10. Все три языка знают 5 человек. Один из студентов вышел. Определить вероятности следующих событий:

1. Вышедший студент знает английский и французский языки. Решение. Введем события:

• А - знает английский;

• В - знает французский. Тогда

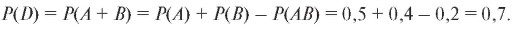
2. Знает английский или немецкий языки. Решение. Событие: С - знает немецкий. Тогда

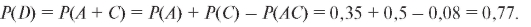
3. Знает немецкий или французский языки. Решение.

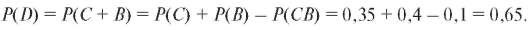
4. Кроме английского языка, знает или французский, или немецкий. Решение.

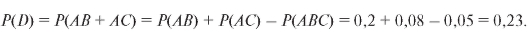
Из формулы сложения вероятностей можно вывести несколько следствий.

Следствие 1. Если события А и В несовместны, то

)

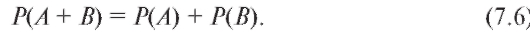Пример 4. Определить вероятность того, что партия из 15 изделий, среди которых 5 бракованных, будет принята после выборочного контроля 4 вместе взятых изделий. Условием приемки является обнаружение не более одного бракованного среди 4 проверяемых изделий.

Решение. Введем обозначения:

• А - событие, состоящее в том, что партия изделий принята;

• В - все четыре проверяемые изделия качественные;

• С - среди четырех проверяемых одно изделие бракованное. Очевидно, что А = В + С (причем события В и С несовместны),

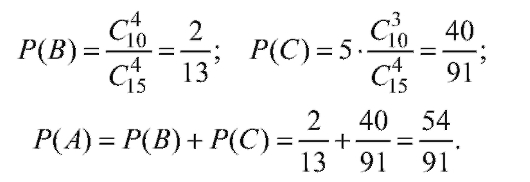
Следствие 2. Если события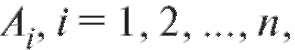попарно несовместны, т. е.

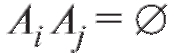для любых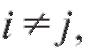то

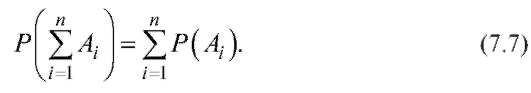
Пример 5. В клетке находится 10 мышей, причем 4 из них серые. Наугад берут трех мышей. Найти вероятность того, что хотя бы одна мышь серая.

Решение. Определим события:

• А - одна мышь серая, две - нет;

• В - две серые, одна - нет;

• С - все серые;

• D - ни одной серой;

• Е - хотя бы одна мышь серая.

События А, В и С являются несовместными, поэтому

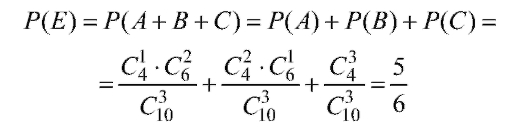
или (с учетом того, что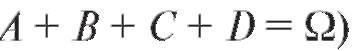

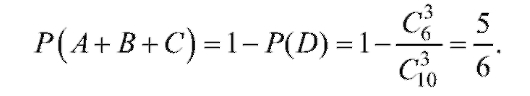
7.1.5. Статистическое определение вероятностей

Классическое определение вероятностей, по существу, сводит понятие «вероятности» к понятию «равновозможности». Однако «равновозможность», представляя собой объективное свойство испытаний, определяемое условиями эксперимента, может быть установлена лишь с известной степенью точности.

Наше представление о симметричных игральных костях, монетах и т. п. было бы только иллюзией, не подтверждай правоту сделанных предположений данные опыта.

Многочисленные эксперименты открыли путь для статистического подхода к численному определению вероятностей, который особенно важен тогда, когда из теоретических соображений, подобных соображениям симметрии, значение вероятности заранее установить нельзя.

В соответствии с этим подходом вероятностью события А называется объективно существующая величина, около которой группируются относительные частоты наступления этого события при неограниченном увеличении числа испытаний.

Другими словами,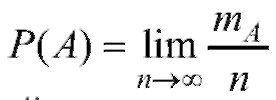, где n - общее число испытаний, а

m_A - число испытаний, в которых событие А наступило. Разумеется, условия, при которых проводится эксперимент, не должны изменяться от опыта к опыту.

Близость частоты и вероятности при многократном повторении одних и тех же экспериментов объясняется так называемым законом больших чисел.

Отметим, что статистическое и классическое определения вероятностей, как, впрочем, и все остальные (геометрическое, аксиоматическое), согласованы, т. е. при решении одних и тех же задач приводят к одинаковым результатам.

Пример 1. Еще в XVIII веке было замечено, что среди обычной корреспонденции письма без адреса обладают определенной устойчивостью, приблизительно 25-27 на каждый миллион.

Пример 2. Относительная частота рождений мальчиков не зависит от местности или этнического состава населения и приблизительно равняется 0,515.

Пример 3. При бросании симметричной монеты вероятность выпадения герба на основании классического определения будет, очевидно, равна 0,5. Английский статистик К. Пирсон (1857-1936) бросил симметричную монету 24 000 раз, при этом герб выпал 12 012 раз, следовательно, относительная частота выпадения герба оказалась равной 0,5005, т. е. как и ожидалось, оказалась примерно равной 0,5.

7.1.6. Условные вероятности. Независимость событий

Рассмотрим вопрос о том, как определить вероятность какого-либо события А при условии, что уже произошло другое событие B.

Пусть, для примера, брошена игральная кость и нам неизвестен результат, однако известно, что выпало четное число очков. Мы же хотим, располагая этой информацией, найти вероятность того, что выпало число больше трех. Речь, следовательно, идет об условной вероятности события А = {выпало число больше трех} при условии, что произошло событие В = {выпало четное число} (обозначается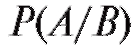) - рис. 7.5.

Поскольку нам известно, что выпало либо 2, либо 4, либо 6 очков, и эти исходы равновозможны, а в такой ситуации событию А благоприятствуют лишь исходы 4 и 6, естественно считать, что

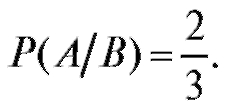Формально это можно объяснить следующим образом: так как событие В произошло, мы в качестве нового пространства элементарных исходов берем все исходы, которые принадлежат В, а

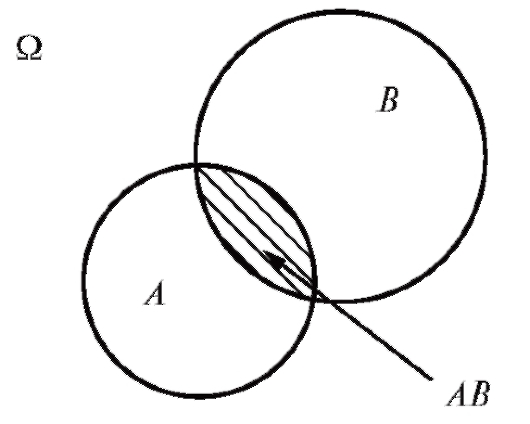
Рис. 7.5. Иллюстрация к процедуре вычисления условной вероятности P(A/B)

благоприятствующими наступлению события А считаем исходы, входящие в А и В одновременно.

Таким образом, по формуле классической вероятности

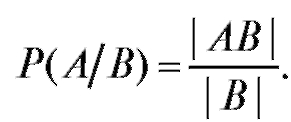
Принимая во внимание то, что последнее равенство можно переписать в виде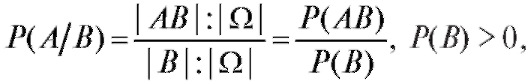приходим к следующему, согласующемуся с интуицией, определению.

Определение. Условная вероятность события А при условии, что произошло событие В с положительной вероятностью, задается формулой

В уже рассмотренном примерекак и

было сказано.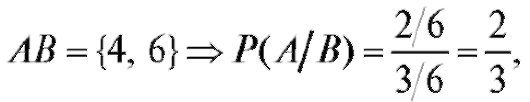

Из формулы (7.8) следует, что условная вероятность - это обычная вероятность, заданная на более узком пространстве элементарных исходов, поэтому для нее справедливы все свойства обычной вероятности.

В частности

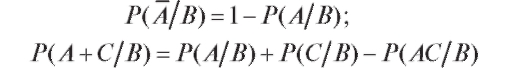
(формула сложения условных вероятностей).

Из равенства (7.8) вытекает формула умножения вероятностей:

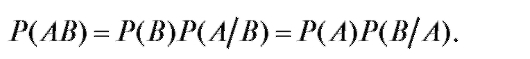(7.9)

Пример 1. В ящике m белых и n черных шаров. Какова вероятность вытащить подряд два белых шара?

Решение. Событие, вероятность которого требуется вычислить, можно представить в виде произведения событий АВ, где А = {первый шар белый}, В = {второй шар белый}. Вероятность события А вычисляется по

формуле (7.3) и равна 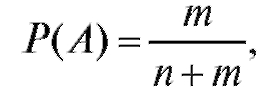условная вероятность

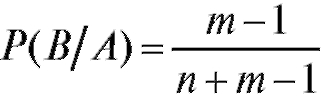(если А произошло, то в ящике осталось (m - 1) белых

шаров, а всего - (m + n - 1) шаров). Остается воспользоваться формулой умножения вероятностей (7.9):

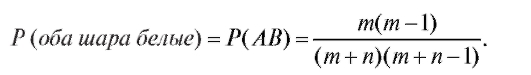
Тот же результат может быть получен с помощью формулы (7.3):

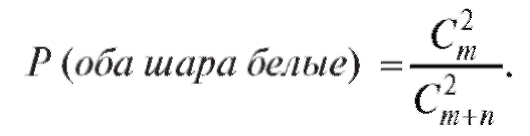
Формулу умножения вероятностей можно обобщить на случай n произвольных событий: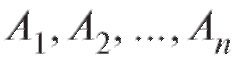

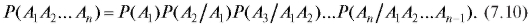
Определение. События А и В называются независимыми, если

Отсюда и из формулы умножения вероятностей следует, что

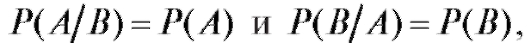т. е. вероятность наступления события А не зависит от того, произошло В или нет (и наоборот). Так, если в ситуации примера 1, вытащив белый шар, вернуть его в ящик, то

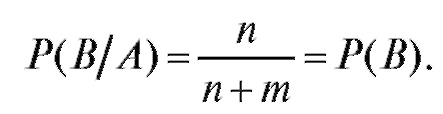
Заметим, что из формулы сложения вероятностей (7.5) и из (7.11) следует, что если события А и В являются независимыми, то

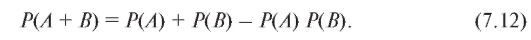
Аналогично (7.11) определяется взаимная независимость событий 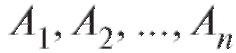в случае которой, в частности (см. также (7.4) и свойство 5),

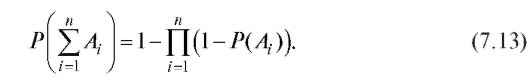
С помощью формулы (7.13) очень просто сосчитать вероятность наступления хотя бы одного из n взаимно независимых событий.

Отметим, что понятие независимости отвечает всем интуитивным представлениям о независимости. В частности, если независимы события А и В, то независимы также события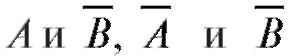и т. д.

Пример 2. Некоторая вакцина эффективна на 75 % в формировании иммунитета. Вакцинировали двух человек. Пусть А и В - независимые события, состоящие в том, что соответственно первый и второй человек приобретают иммунитет. Найти вероятность того, что:

а) оба человека приобрели иммунитет;

б) первый приобрел иммунитет, а второй - нет;

в) оба не приобрели иммунитета. Решение.

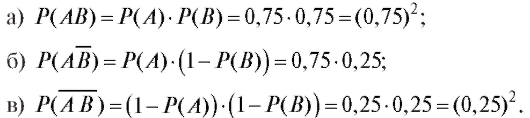
7.1.7. Формула полной вероятности

Определение. Набор попарно несовместных событий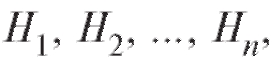 сумма которых составляет достоверное событие, называется полной группой событий.

Теорема 7.5 (формула полной вероятности). Пусть события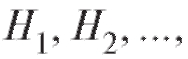 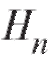являются полной группой событий. Тогда для любого события А

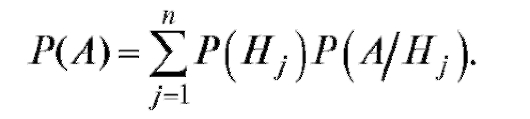(7.14)

Доказательство. В силу свойств операций над событиями (см.

п. 7.1.2)

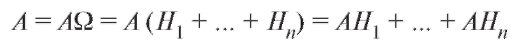
Поскольку события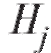попарно несовместны, то и событияобладают тем же свойством. Поэтому в силу следствия 2 (см. (7.7))

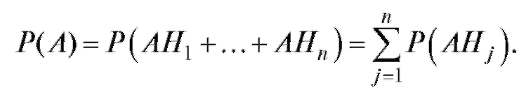
Остается применить к слагаемым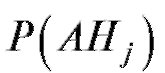формулу умножения ве-

роятностей.

Пример 1. Команда на хорошем поле выигрывает с вероятностью 2/3, а на плохом - с вероятностью 1/2. Известно, что 3/4 игр проводится на хорошем поле. Какова вероятность выиграть в выбранном наудачу матче?

Решение. Введем события А = {выигрыш},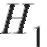= {плохое поле},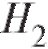= {хорошее поле}. По условиям примера:

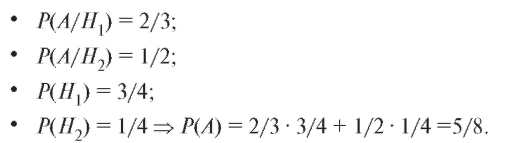
Пример 2. Вероятность брака при изготовлении детали равна 0,04. Приемка деталей производится по следующей системе контроля: годная деталь принимается с вероятностью 0,98, а бракованная - с вероятностью 0,1. Найти вероятность приемки детали.

Решение. Пусть событие А - деталь принята,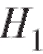- изготовлена хорошая деталь,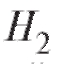- изготовлена бракованная деталь. Из условий найдем соответствующие вероятности:

А также: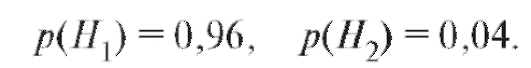

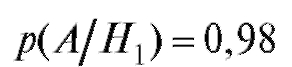• - вероятность того, что принятая деталь хорошая;

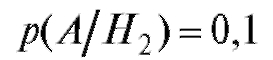• - вероятность того, что принятая деталь бракованная. Вероятность того, что деталь будет принята, на основании формулы

(7.14) равна

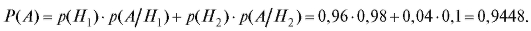
Пример 3. Имеются три одинаковых ящика с шарами. В первом ящике 30 белых и 20 черных шаров, во втором - 15 белых и 15 черных шаров, в третьем - 5 белых и 15 черных шаров. Какова вероятность вытащить из случайно выбранного ящика черный шар?

Решение. Обозначим события:

• - выбран первый ящик;

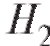• - выбран второй ящик;

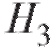• - выбран третий ящик.

Поскольку выбор того или иного ящика - события равновероятные, то

А также: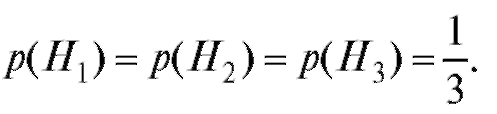

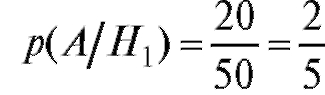• - вероятность того, что черный шар вытащили из первого ящика;

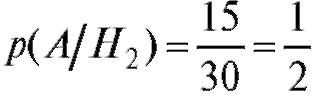• - вероятность того, что черный шар вытащили из второго ящика;

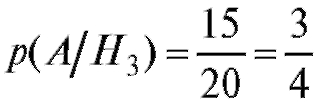• - вероятность того, что черный шар вытащили

из третьего ящика. По формуле (7.14) найдем искомую вероятность

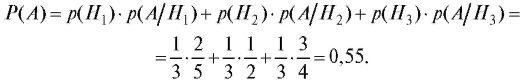
7.1.8. Формулы Бернулли и Пуассона

Схемой Бернулли будем называть схему одинаковых независимых испытаний, каждое из которых заканчивается одним из двух несовместных исходов: или наступает некоторое событие А, или оно не наступает, т. е. наступает противоположное ему событие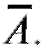Независимость испытаний означает, что вероятность события А в любом испытании не зависит от того, какими сведениями мы располагаем относительно результатов других испытаний. Кроме того, в схеме Бернулли предполагается, что вероятность события А в одном испытании остается постоянной во всей серии испытаний.

Многие практически важные задачи приводят к отысканию вероятности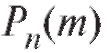того, что при n испытаниях, произведенных по схеме Бернулли, событие А произойдет m раз (m = 0, 1, 2, n), если известна вероятность р события А в каждом испытании. Справедлива следующая формула Бернулли:

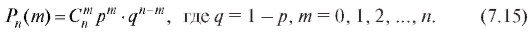
Пример 1. Что вероятнее выиграть у равносильного противника:

а) три партии из четырех или пять из восьми;

б) не менее трех партий из четырех или не менее пяти партий из восьми? Решение. Так как противники равносильны, то вероятности выигрыша и проигрыша в каждой партии одинаковы.

а) вероятность выиграть три партии из четырех:

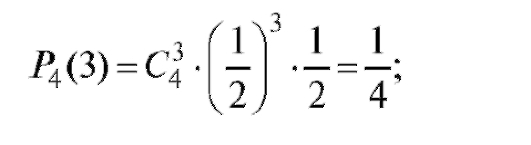
вероятность выиграть пять партий из восьми:

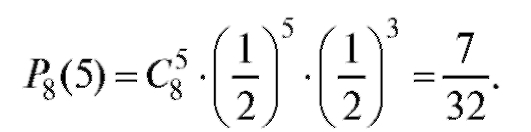
Так как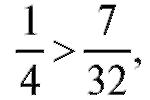то вероятнее выиграть три партии их четырех.

б) вероятность выиграть не менее трех партий из четырех:

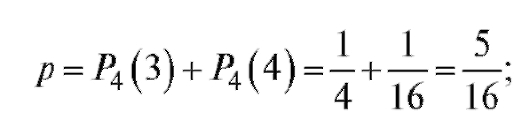
вероятность выиграть не менее пяти партий из восьми:

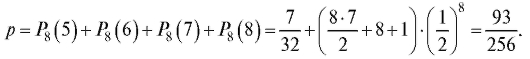
Посколькуто вероятнее выиграть не менее пяти партий из

восьми.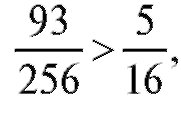

Пример 2. Студент отвечает на 4 дополнительных вопроса при сдаче экзамена. Вероятность правильного ответа на каждый вопрос будем

считать равной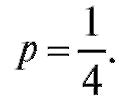Предполагая, что все ответы - события незави-

симые, найти вероятность того, что будут даны хотя бы два правильных ответа.

Решение. А = {хотя бы два правильных ответа} - это 2, 3 или 4.

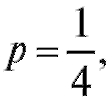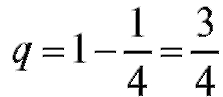Так както - вероятность неправильного ответа

на вопрос. Эту задачу удобно решать, используя противоположные события, т. е. пользуясь равенством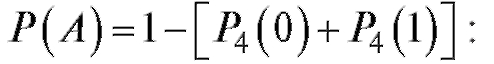

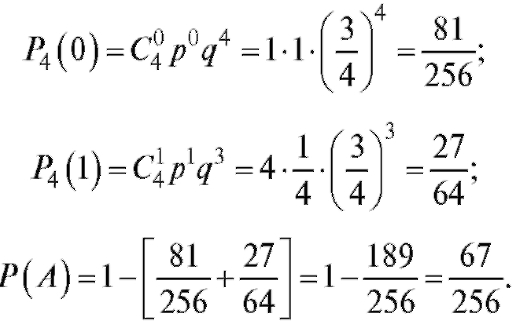
В случаях, когда в (7.15) n велико, а р мало, вместо формулы Бернулли, как правило, ограничиваются формулой Пуассона:

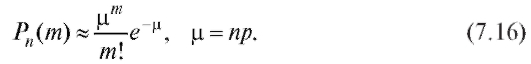
Пример 3. При перевозке 1000 стеклянных колб вероятность разбить 1 колбу равна 0,002. Какова вероятность того, что будут разбиты 4 колбы?

Решение.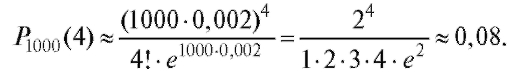

Самостоятельная работа Комбинаторика

1. Сколькими способами можно выбрать 3 различных краски из имеющихся 5?

2. Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов?

3. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из 5 языков - русского, английского, французского, немецкого и итальянского - на любой другой из этих 5 языков?

4. Составляются знаки, состоящие из геометрической фигуры (окружность, квадрат, треугольник или шестиугольник), буквы и цифры. Сколько таких знаков можно составить?

5. Для эксперимента по определению скорости роста требуется выбрать 4 штамма бактерий из имеющихся 8. Сколькими способами это можно сделать?

Классическая вероятность

6. Студент знает 40 вопросов из 60, включенных в программу. Найти вероятность того, что студент знает 2 вопроса, содержащихся в его экзаменационном билете?

7. В одном аквариуме находятся 5 белых, 4 красных и 3 голубых рыбки. Двух случайно выбранных рыбок переносят в другой аквариум. Какова вероятность того, что обе рыбки голубые?

8. Из десяти билетов выигрышными являются два. Определить вероятность того, что среди взятых наудачу пяти билетов:

а) один выигрышный;

б) два выигрышных;

в) хотя бы один выигрышный.

9. Набирается четырехзначный номер телефона. Какова вероятность набрать его правильно с первого раза, если все цифры номера нечетные и ровно три из них пятерки?

10. Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наугад выбирают 5 человек на конференцию. Найти вероятности следующих событий:

• А - будут выбраны одни третьекурсники;

• В - все первокурсники попадут на конференцию;

• С - не будет выбран ни один второкурсник;

• D - выберут одного первокурсника, двоих второкурсников и двоих третьекурсников.

Сложение и умножение вероятностей

11. На клумбе растут 20 красных, 30 синих и 40 белых астр. Какова вероятность сорвать в темноте окрашенную астру, если срывают одну астру?

12. Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если после первого отказа отвечать на вопрос преподаватель задает еще один вопрос?

13. Шесть человек больны заболеванием, для которого коэффициент выздоровления составляет 98 %. Какова вероятность того, что:

а) выздоровеют все шестеро;

б) выздоровеют только пятеро?

14. В читальном зале 6 учебников по теории вероятности, из которых 3 в переплете. Библиотекарь взял наугад 2 учебника. Найти вероятность того, что оба учебника окажутся в переплете.

15. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго - 0,8. Найти вероятность того, что при одном залпе в мишень попадет только один из стрелков.

16. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.

17. В цехе работают 7 мужчин и 3 женщины. По табельным номерам наугад отобраны 3 человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.

18. Некто написал 3 письма, запечатал их в конверты, а затем наугад на каждом из них написал различные адреса. Определить вероятность того, что на всех конвертах написан правильный адрес.

Формула полной вероятности

19. В первой коробке 20 ампул, из них 18 стандартных, во второй - 10 ампул, из них 9 стандартных. Из второй коробки взята наугад ампула и переложена в первую коробку. Найти вероятность того, что случайным образом извлеченная из первой коробки ампула окажется стандартной.

20. В вычислительной лаборатории имеются 6 клавишных автоматов и 4 полуавтомата. Вероятность того, что за время выполнения расчета автомат не выйдет из строя, равна 0,95, а для полуавтомата эта вероятность равна 0,8. Студент выполняет расчет на машине, выбранной наугад. Найти вероятность того, что до окончания расчета машина не выйдет из строя.

21. В первой коробке 3 белых шарика и два черных, во второй - 2 белых и 3 черных, в третьей - 1 белый и 2 черных. Наугад выбирается коробка и из нее два шарика. Какова вероятность того, что они разных цветов?

Формула Бернулли

22. Монету бросают 6 раз. Найти вероятность того, что герб выпадает:

а) менее двух раз;

б) не менее двух раз.

23. Производится серия из 4 выстрелов по мишеням с вероятностью попадания в каждом выстреле p = 1/4. Предполагая, что результаты выстрелов - события независимые, найти вероятность того, что будут хотя бы два попадания.

24. Монету подбрасывают 8 раз подряд. Какова вероятность того, что герб выпадет 5 раз?

25. В библиотеке имеются учебники по химии и биологии. Вероятность того, что любой читатель возьмет книгу по химии, равна 0,7, а по биологии - 0,3. Определить вероятность того, что 5 читателей подряд возьмут книги или только по химии, или только по биологии, если каждый берет только одну книгу.

Формула Пуассона

26. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия (остальные - годные!).

27. Среди семян ржи 0,4 % семян сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?

7.2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

До сих пор мы изучали способы вычисления вероятностей различных случайных событий. При этом под случайными событиями понималась любая качественная характеристика результата испытания. Однако существует много задач, решение которых требует изучения явлений, характер которых определяется не фактом появления или не появления того или иного случайного события, а зависит от некоторых величин, способных принять иные случайные значения. Такие величины в теории вероятностей называются случайными. Таким образом, если случайное событие есть качественная характеристика испытания, то случайная величина является количественной характеристикой испытания. Следует заметить, что понятие случайной величины является в известном смысле обобщением понятия случайного события, так как каждому случайному событию А можно всегда поставить в соответствие случайную величину, принимающую два значения, например 1 или 0, в зависимости от того, произошло событие А в результате данного испытания или не произошло.

Приведем примеры случайных величин:

• продолжительность жизни любого живого существа;

• число дефектных изделий в любой выборке данного объема;

• прибыль предприятия за любой фиксированный отрезок времени;

• погрешность любого измерения;

• время безотказной работы любого технического устройства;

• отклонения параметров данного устройства от номинальных значений.

Приведенные примеры с достаточной определенностью показывают, что со случайными величинами приходится иметь дело в самых разнообразных областях науки и техники.

Для полной характеристики случайной величины необходимо знать:

• множество ее возможных значений;

• как часто, т. е. с какой вероятностью, случайная величина принимает те или иные значения.

Такая характеристика случайной величины называется ее законом распределения. Закон распределения случайной величины может быть задан в различных формах в зависимости от типа случайной величины. Тип случайной величины определяется видом множества значений, которые может принимать рассматриваемая случайная величина. Особую

важность для технических приложений имеют два типа случайных величин: дискретного и непрерывного типа.

Определение. Случайная величина называется величиной дискретного типа или просто дискретной, если она может принимать конечное или счетное множество значений.

Определение. Случайная величина называется величиной непрерывного типа, если она может принимать любые значения в одном или нескольких заданных интервалах.

7.2.1. Закон распределения вероятностей дискретной случайной величины

Рассмотрим дискретную случайную величину X c конечным множеством значений

Определение. Совокупность всех значений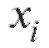случайной величины X и соответствующих этим значениям вероятностей 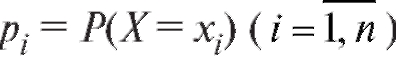называется законом распределения X.

Закон дискретной случайной величины может быть задан с помощью табл. 7.1.

Таблица 7.1

Очевидно, что всегда должно быть выполнено условие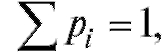 так как события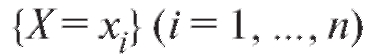образуют полную группу событий.

Важный пример дискретной случайной величины дает число m появлений некоторого события в серии последовательных испытаний, проведенных по схеме Бернулли.

Обозначим через X число появлений события А в n испытаниях, и пусть вероятность наступления события А в каждом испытании равна p.

Говорят, что случайная величина X имеет биномиальное распределение с параметрами n и p, если

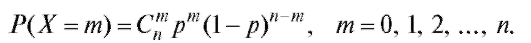
Еще одним примером дискретной случайной величины является случайная величина X, имеющая распределение Пуассона с параметром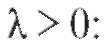

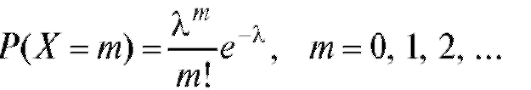
Напоминаем, что распределение Пуассона является предельным для биномиального распределения (см. п. 7.1.3). Отметим также, что случайная величина X, имеющая распределение Пуассона, принимает бесконечное число значений.

Закон распределения дискретной случайной величины можно задавать по-другому, а именно с помощью так называемого интегрального закона распределения, или функции распределения вероятностей.

Определение. Функцией распределения F(x) случайной величины X называется вероятность того, что величина X примет значение, меньшее чем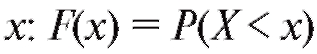, где x - произвольное вещественное число.

Заметим сразу же, что функция распределения вероятностей F(x) случайной величины Х является универсальной характеристикой Х, она существует для случайной величины любого типа.

Очевидно, что если Х - дискретная случайная величина, то ее функция распределения определяется посредством равенства

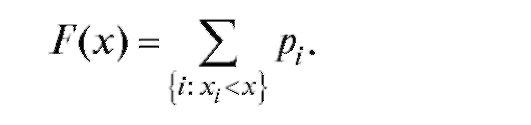(7.17)

Пример 1. Построить функцию распределения дискретной случайной величины Х, если известен ее закон распределения (табл. 7.2).

Таблица 7.2

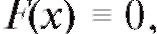Решение. Еслитопоскольку в данном случае событие

является невозможным.

Еслито событие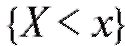равносильно событию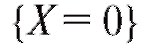. Поэтому для данного промежутка 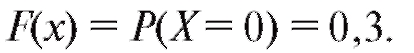Аналогично, если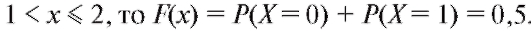

Наконец, если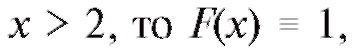поскольку теперь событие 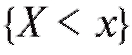становится достоверным. Итак, функция распределения такова:

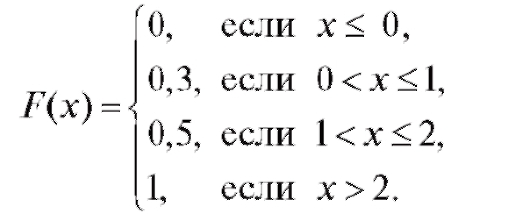
График данной функции распределения представлен на рис. 7.6.

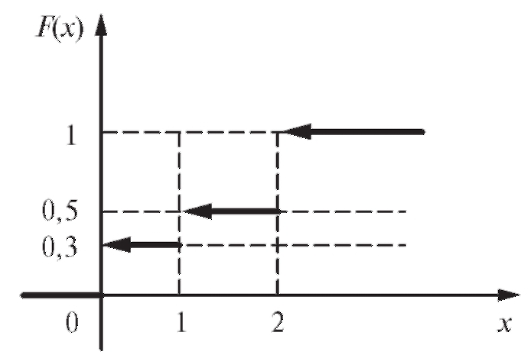
Рис. 7.6. Функция распределения дискретной случайной величины

График F(x) дискретной случайной величины и в общем случае оказывается ступенчатым со скачками в точкахрав-

ными соответственно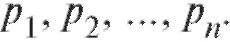 Само распределение дискретной случайной величины также называется дискретньм.

Пример 2. Построить ряд распределения случайной величины Х, представляющей собой число выпадения герба при двукратном бросании монеты.

Решение. Рассчитаем, а затем заполним табл. 7.3.

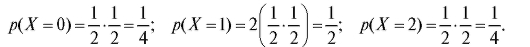
Таблица 7.3

Пример 3. Из партии в 25 изделий, среди которых имеются 6 бракованных, выбраны случайным образом 3 изделия для проверки их качества. Построить ряд распределения случайного числа бракованных изделий, содержащихся в выборке.

Решение. Рассчитаем, а затем заполним табл. 7.4.

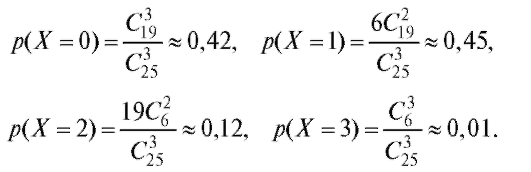
Таблица 7.4

7.2.2. Функция распределения и плотность вероятности непрерывной случайной величины

Пусть Х является случайной величиной непрерывного типа. Множество значений такой случайной величины несчетно, поэтому мы не можем выписать в последовательность и занумерованность все ее значения и, следовательно, не можем задать ее закон распределения в виде таблицы. В этом случае на помощь приходит функция распределения, с помощью которой можно характеризовать закон распределения случайной величины любого типа. Случайная величина Х (любого типа) считается заданной, если известна ее функция распределения, т. е. функция

Рассмотрим некоторые основные свойства функции распределения F(x) произвольной случайной величины Х.

Прежде всего, как всякая вероятность, F(x) удовлетворяет при любом х неравенству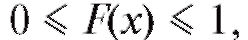так что график функции y = F(x) всегда лежит в полосе между прямыми y = 0, y = 1.

При помощи функции распределения F(x) можно всегда определить вероятность попадания случайной величины Х на промежуток [а; р) при любых значениях а и р.

В самом деле, если через А обозначить событие, состоящее в том, что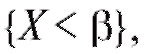через В - событие, со-

стоящее в том, чтои, нако-

нец, через С - событие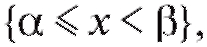 то очевидно, что А = В + С.

Следовательно, по правилу сложения вероятностей для несовместимых событий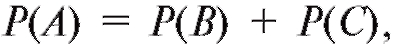откуда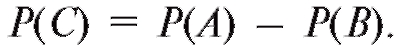Но

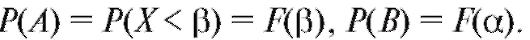
Поэтому окончательно

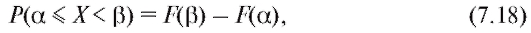
т. е. вероятность попадания случайной величины в промежуток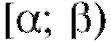 равна приращению функции распределения на этом промежутке.

Так как вероятность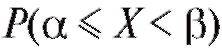неотрицательна, как всякая вероят-

ность, то из последнего равенства следует, чтоесли

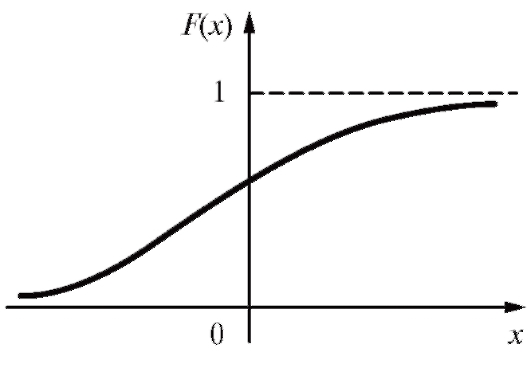
Рис. 7.7. Функция распределения непрерывной случайной величины

т. е. функция распределения любой случайной величины является неубывающей функцией.

Если случайная величина Х является ограниченной, т. е. все ее возможные значения лежат в каком-либо конечном отрезке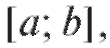мы будем иметь равенства

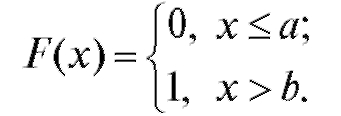
В общем случае, когда величина Х может быть и неограниченной, будут иметь место следующие соотношения:

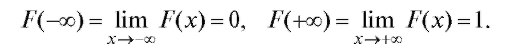
Примером может служить функция распределения случайной величины, распределенной по показательному закону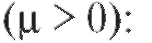

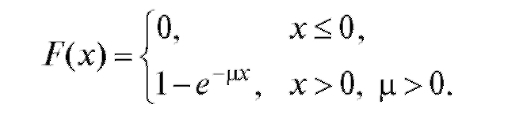(7.19)

Если случайная величина Х принадлежит к непрерывному типу, то для любого x имеем равенство

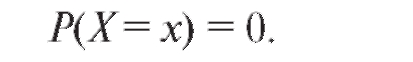
Напомним, что для дискретных случайных величин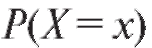отлично

от нуля, если x совпадает с каким-либо частным значением этой случайной величины.

Таким образом, любая непрерывная случайная величина Х не может быть характеризована вероятностями своих значений, поскольку все эти вероятности равны нулю.

Чтобы преодолеть эту трудность, вводится понятие плотности вероятности.

Определение. Плотностью вероятности, или дифференциальным законом распределения вероятностей, случайной величины Х называется функция f (x), определяемая равенством

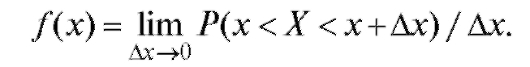
Рассмотрим свойства плотности вероятности.

Во-первых, очевидно, что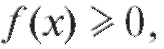поскольку вероятность неотрица-

тельна.

Во-вторых, числитель правой части последней формулы может быть заменен разностью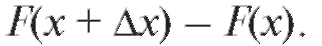

На основании определения производной получим выражение плотности вероятности через функцию распределения:

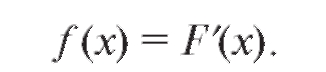(7.20)

Третье свойство плотности вероятности может быть получено, если сопоставить равенство (7.18) для непрерывной случайной величины с формулой Ньютона-Лейбница

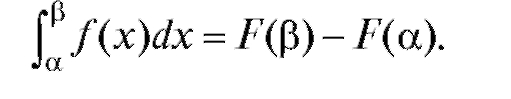(7.21)

Это сопоставление позволяет получить выражение для вероятности попадания случайной величины Х непрерывного типа в интервал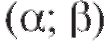 через ее плотность вероятности f (x):

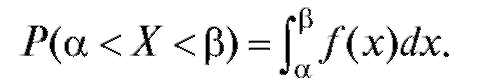(7.22)

Заменяя в последнем равенствеи пользу-

ясь определением функции распределения, получим четвертое свойство плотности вероятности, позволяющее найти функцию распределения, если известна плотность вероятности:

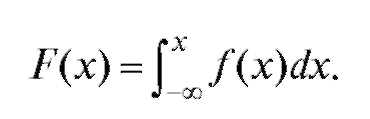(7.23)

Последнее, пятое свойство получим, если верхний предел х интеграла в последней формуле устремим к:

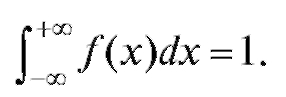(7.24)

Это означает, что площадь, ограниченная осью абсцисс и графиком плотности вероятности, равна 1.

Отметим, что не всякая непрерывная случайная величина Х имеет плотность вероятности, но лишь та, функция распределения которой дифференцируема.

Пример 1. Дана функция распределения непрерывной случайной величины Х:

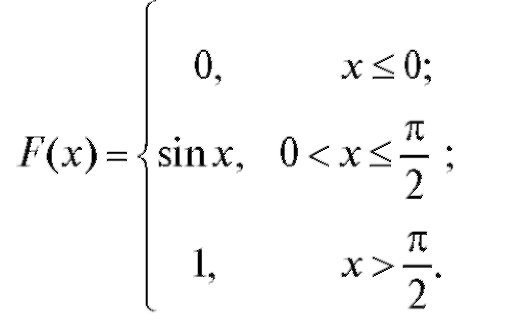
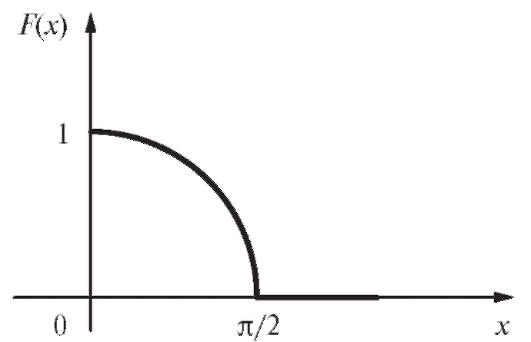
Рис. 7.8. Плотность распределения

Найти плотность вероятности f (x) и построить ее график. Решение.

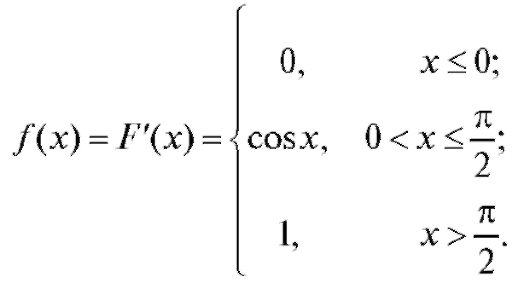
График плотности приведен на рис. 7.8.

Пример 2. Дана плотность распределения случайной величины Х:

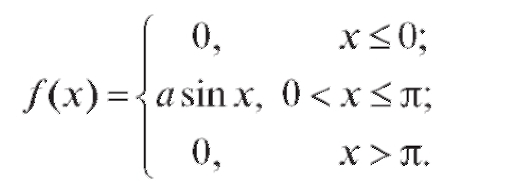
Определить коэффициент а и функцию распределения F(x). Решение.

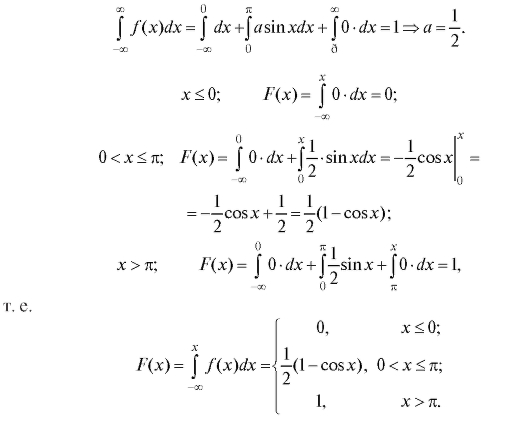
7.2.3. Числовые характеристики случайных величин

Для полной характеристики распределения случайной величины Х необходимо знать, как мы видели, ее функцию распределения или, в случае непрерывной Х, ее плотность вероятности. Однако в ряде практических задач нет необходимости в таком полном исследовании случайной величины Х, и бывает достаточно иметь хотя бы грубое представление о распределении Х, описать его посредством немногих простых параметров. В ряде случаев достаточно знать:

• примерное расположение того интервала значений, в котором находится основная масса вероятности случайной величины Х, а также положение «центра группирования» на числовой оси;

• насколько широко разбросаны значения случайной величины Х по каждую сторону от «центра группирования».

Параметры первого рода, характеризующие положение центра группирования, называются характеристиками расположения (или положения); параметры второго рода, характеризующие разброс значений случайной величины около центра группирования, называются характеристиками рассеивания.

Наиболее часто употребляемой характеристикой расположения является так называемое математическое ожидание случайной величины Х, которое будем обозначать символом М (Х). Рассмотрим сначала математическое ожидание дискретной случайной величины Х, заданной таблицей распределения (см. табл. 7.1). Математическое ожидание такой величины есть по определению сумма произведений всех ее возможных частных значений на соответствующие им вероятности:

Если возможные значения дискретной случайной величины Х составляют счетное множество и она задана рядом распределения

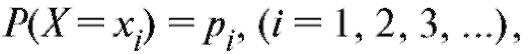то по определению математическое ожидание Х равно сумме ряда:

Математическое ожидание непрерывной случайной величины с плотностью вероятности f (x) определяется равенством

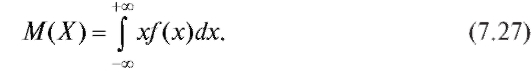
Пример 1. Найти математическое ожидание случайной величины, принимающей значения 1 и 0, с вероятностью р и q = 1 - p соответственно.

Решение. По определению математического ожидания имеем

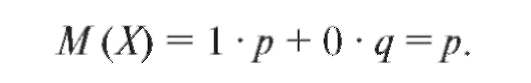
Перейдем к перечислению основных свойств математического ожидания.

Свойство 1. Математическое ожидание постоянной равно этой постоянной, т. е. если С - константа, то М (С) = С.

Свойство 2. Математическое ожидание суммы произвольных случайных величин равно сумме их математических ожиданий:

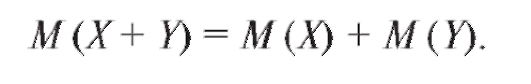
Следствие. Математическое ожидание суммы конечного числа произвольных случайных величин равно сумме их математических ожиданий, т. е.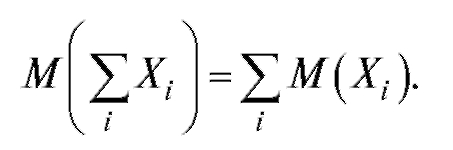

Пример 2. Найти математическое ожидание числа X наступлений события А при n независимых испытаниях, в каждом из которых событие А появляется с вероятностью p или не появляется с вероятностью q = 1 - p. Другими словами, X имеет биномиальное распределение с параметрами n и p (см. п. 7.2.1).

Решение. Очевидно, что X может быть представлено в виде суммы:

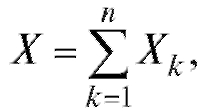где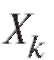есть случайная величина, равная единице, если событие А произошло в k-м испытании, и нулю, если событие А не произошло. Таким образом,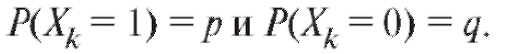

На основании последнего свойства математического ожидания имеем:

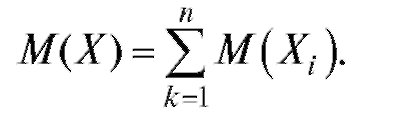
3. Дисперсия случайной величины равна разности математического ожидания квадрата случайной величины и квадрата математического

ожидания, т. е.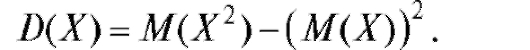

4. Если С - константа, то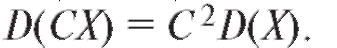

5. Дисперсия суммы или разности независимых случайных величин равна сумме их дисперсий: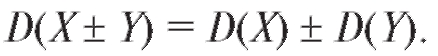

Последнее свойство остается справедливым для любого конечного числа попарно независимых случайных величин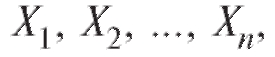т. е.

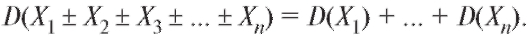
Пример 3. Найти дисперсию случайной величины Х, которая имеет биномиальное распределение с параметрами n иp (см. пример 2).

Решение. Как показано в примере 2, справедливо равенство

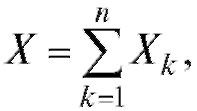где все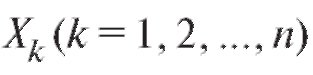

попарно независимы и имеют закон распределения, представленный в табл. 7.5.

Таблица 7.5

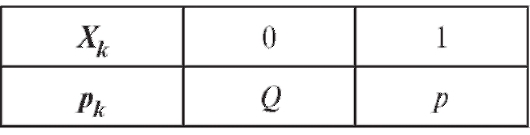
На основании свойства 5 дисперсии имеем равенство

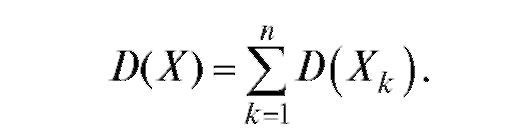
На основании свойства 3 имеем равенство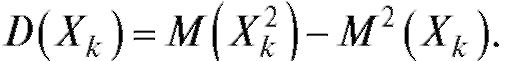 Ранее было найдено, что 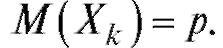Очевидно, что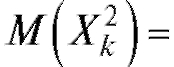

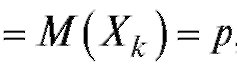, следовательно, 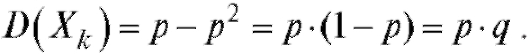Оконча-

тельно получаем: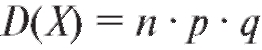, т. е. дисперсия случайной величины X,

имеющей биномиальное распределение с параметрами n и p, равна

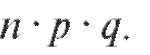
В некотором отношении более удобна не дисперсия, а другая мера рассеивания случайной величины Х, которая чаще всего и используется, - это корень квадратный из дисперсии, взятый с положительным знаком. Эта мера называется средним квадратичным отклонением или стандартным отклонением случайной величины.

Стандартное отклонение обычно обозначается символом о_х или о(Х):

Удобство стандартного отклонения состоит в том, что оно имеет размерность самой случайной величины Х, в то время как размерность дисперсии - квадрат разномерности Х.

В заключение отметим, что дисперсия среднего арифметического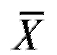 из п независимых одинаково распределенных случайных величин Х₁, равна дисперсии какой-либо из этих величин, деленной на их число:

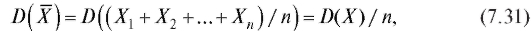
и, в частности,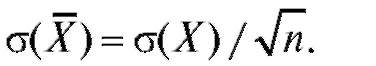

Именно так обстоит дело, когда мы производим п измерений какойлибо физической величины. Важно то, что результат каждого измерения не зависит от результатов отдельных измерений; тогда последовательные измерения можно рассматривать как значения независимых и одинаково распределенных случайных величин. Средняя квадратичная ошибка одного измерения (стандартное отклонение Х) будет при этом о(Х), а средняя квадратичная ошибка среднего арифметического Х из п измерений будет в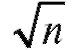раз меньше средней квадратичной ошибки одного измерения. Следует заметить, что если в опыте наш прибор давал систематическую ошибку, то никакими повторениями опыта от нее не избавиться.

Замечание. Совместный закон распределения и числовые характеристики двух случайных величин обсуждаются в п. 7.2.5.

7.2.4. Нормальный закон распределения

Среди непрерывных распределений наиболее важную роль играет нормальное распределение. К нормальному закону распределения, называемому также законом Гаусса, при весьма часто встречающихся условиях приближаются другие законы. В частности, если мы имеем сумму большого числа независимых величин, подчиненных каким угодно законам распределения, то при некоторых всеобщих условиях она будет приближенно подчиняться нормальному закону.

Случайная величина, распределенная по нормальному закону, имеет плотность вероятности вида

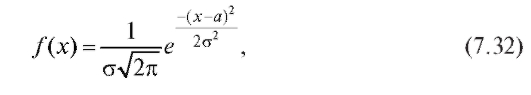
где постоянные а и σ - параметры распределения; график этой плотности схематически изображен на рис. 7.9.

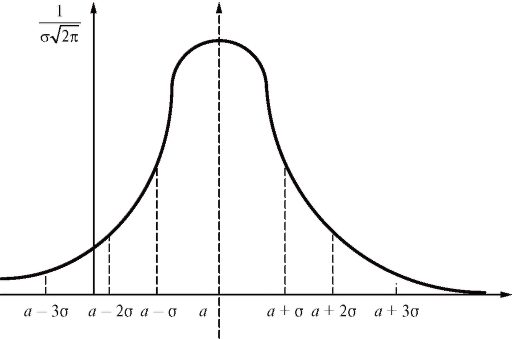
Рис. 7.9. Плотность вероятности нормального распределения

Легко видеть, что f (a + x) = f (a - x), так что кривая плотности симметрична относительно прямой х = а. Методами дифференциального исчисления можно установить, что кривая плотности имеет единственный максимум при х = а и две точки перегиба при х = а ± σ.

Если случайная величина подчинена нормальному закону распределения вероятности с параметрами а и σ, то этот факт для краткости может быть записан в виде Х~ N (а, σ).

Вероятностный смысл параметров а и о выясняется после нахождения математического ожидания и дисперсии случайной величины Х~ N (а, σ). Оказывается, что М (Х) = а, D(Х) = σ^2.

Определенный интеграл с переменным верхним пределом вида

носит название нормированной функции Лапласа или просто функции Лапласа (см. приложение 1).

Функция Лапласа обладает следующими свойствами:

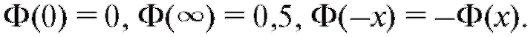
Функция распределения случайной величины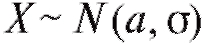может быть

выражена через функцию Лапласа следующим образом:

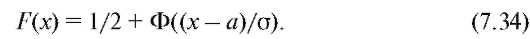
Принимая во внимание формулу (7.34), найдем вероятность попадания случайной величины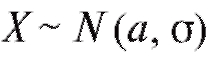в промежуток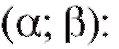

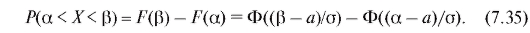
Если промежуток симметричен относительно а (равной М(Х)), то для случайной величины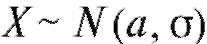получаем формулу следующего вида:

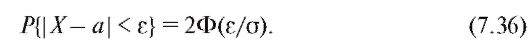
При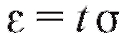получим

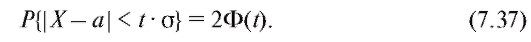
В частности, пользуясь приложением 1, при t = 1, 2, 3 из формулы (7.36) получим

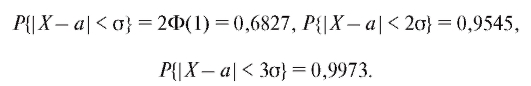
Последнее равенство дает основание к следующему практическому правилу, которое часто называют правиломвсе практически возможные значения случайной величины, подчиненной нормальному закону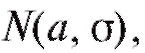заключены в интервале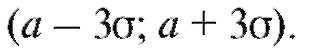

7.2.5. Совместный закон распределения и числовые характеристики двух случайных величин

Для того чтобы в дальнейшем уметь правильно определять выборочные характеристики взаимосвязанных случайных величин, нам понадобятся некоторые сведения из теории вероятностей.

Рассмотрим случайные величины X и Y, получающие свои значения в результате одного и того же случайного эксперимента.

Сначала будем предполагать, что X и Y являются дискретными случайными величинами и принимают значения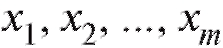и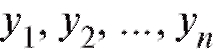 соответственно, где m и п - некоторые целые положительные числа. Для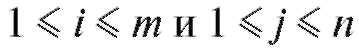определим вероятности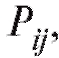положив

т. е.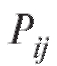равно вероятности того, что события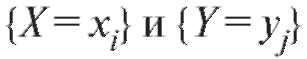произойдут

одновременно.

Определение. Совместным законом распределения пары случайных величин X и Y, или законом распределения двумерного случайного вектора (X, Y) называется соответствие, которое каждой паре значений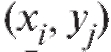 дискретных случайных величин X и Y сопоставляет ее вероятность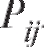. Указанные соответствия можно записать в виде табл. 7.6, в которой

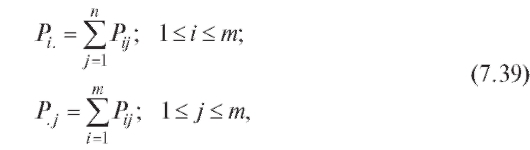
т. е.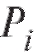равняется сумме вероятностей, расположенных в i-й строке, а равняется сумме вероятностей из j-го столбца.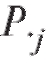

Таблица 7.6

Очевидно, что 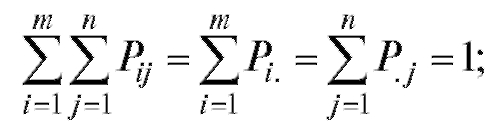кроме того,

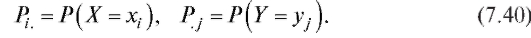
Таким образом, индивидуальные законы распределения собственно случайных величин X и Y можно записать в виде табл. 7.7 и 7.8.

Таблица 7.7

Таблица 7.8

Определение. Дискретные случайные величины X и Y называются независимыми, если при любых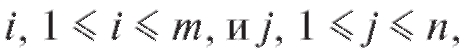выполняются соотношения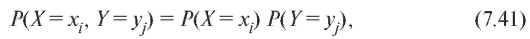

или (см. (7.39)), равносильно,.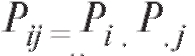

Таким образом, если случайные величины X и Y независимы, то их совместный закон распределения взаимно однозначно определяется по индивидуальным законам распределения (см. табл. 7.6- 7.8). Более интересен случай, когда условие (7.41) не выполняется, и случайные величины X и Y связаны стохастической зависимостью.

Далее приведем некоторые числовые характеристики рассматриваемых дискретных случайных величин X и Y (см. (7.39) и табл. 7.6). Предварительно напомним, что для любой функции двух переменных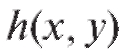 математическое ожидание 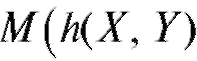случайной величин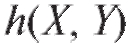ывы-

числяется по формуле

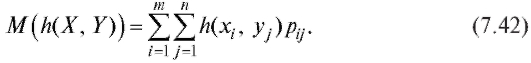
Математические ожидания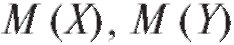случайных величин X и Y, а

также их дисперсии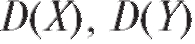и среднеквадратические отклонения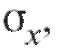

о_у с учетом условия (7.40) рассчитываются по стандартным (см. формулы (7.27), (7.30)) формулам:

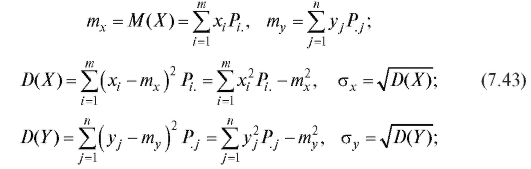
в которых используются лишь данные из табл. 7.7 и 7.8.

Две следующие характеристики случайных величин X и Y, в отличие от предыдущих, в известной степени учитывают связь между этими величинами.

Определение. Ковариацией, или корреляционным моментом, случайных величин X и Y называется число

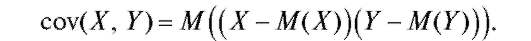
Отметим, что

и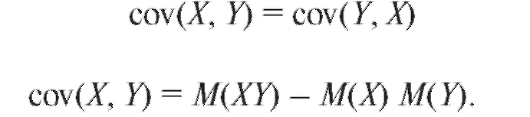

Важным свойством ковариации является то, что для независимых случайных величин X и Y их ковариация обращается в ноль. Отсюда, в частности, следует, что если ковариация двух случайных величин не равна нулю, то они стохастически зависимы. В то же время условие cov(X, Y) = 0 не означает независимость величин X и Y.

Принимая во внимание формулу (7.42), видим, что

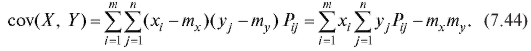
Определение. Коэффициентом корреляции случайных величин X и Y называется число

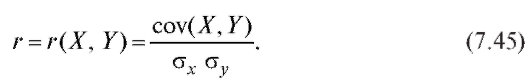
Коэффициент корреляции является безразмерной характеристикой, которая используется в качестве меры линейной зависимости случайных величин. Чем его модуль ближе к единице, тем, вообще говоря, теснее линейная зависимость между величинами.

Графически это означает, что случайным образом выбранные точки (X, Y) с ростом модуля коэффициента корреляции будут в среднем теснее группироваться относительно прямой a + bX.

Корреляционное поле точек (X, Y), изображенное на рис. 7.10, указывает на более тесную линейную зависимость между X и Y (и соответствует большему значению коэффициента корреляции), чем аналогичное корреляционное поле на рис. 7.11.

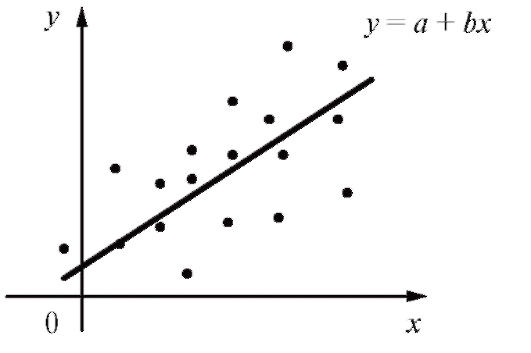
Рис. 7.10. Корреляционное поле точек (X, Y) с менее тесной линейной зависимостью между X и Y

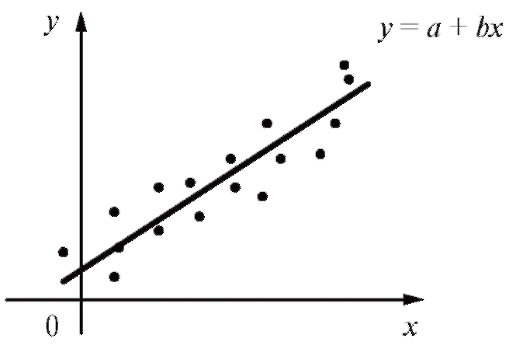
Рис. 7.11. Корреляционное поле точек (X, Y) с более тесной линейной зависимостью между X и Y

Понятно, что коэффициент корреляции и ковариация обращаются в ноль одновременно; следовательно, коэффициент корреляции независимых случайных величин равен нулю.

Определение. Если коэффициент корреляции случайных величин X и Y равен нулю, то такие величины называются некоррелированными.

Перечислим основные свойства коэффициента корреляции.

1.

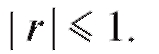
2. | r | = 1 тогда и только тогда, когда Y = a + bX с вероятностью единица, где a и b - некоторые постоянные.

3. Если величины X и Y независимы, то они некоррелированы.

На практике некоррелированность часто отождествляют с независимостью, что, как уже отмечалось, неправомерно. Тем не менее, в важном частном случае совместного нормального распределения величин X и Y некоррелированность и независимость являются равносильными понятиями.

Определение. Прямая, имеющая уравнение

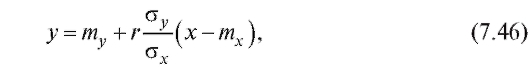
называется прямой средней квадратической регрессии Y на X.

Эта прямая наилучшим (в смысле среднего квадратического) образом приближает случайную величину Y линейной функцией a + b X (можно показать, что дисперсия D (Y - a - bX) минимальна и равна 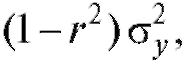когда уравнение у = a + b x имеет вид (7.46)).

Меняя в соотношении (7.46) X и Y ролями, мы получаем прямую средней квадратической регрессии X на Y

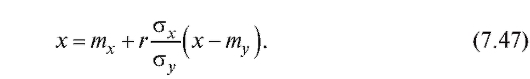
Легко понять, что линии регрессии (7.46) и (7.47) будут совпадать тогда и только тогда, когда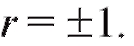

Замечание. Совместный закон распределения может быть определен для пары случайных величин X и Y общего вида и, в частности, для непрерывных случайных величин. В последнем случае равенство (7.38) заменяется его дифференциальным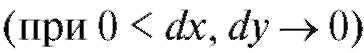аналогом

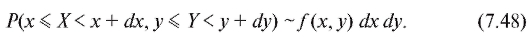
Функция f (x, у) из соотношения (7.48) называется совместной плотностью распределения случайных величин X и Y. Она должна удовлетворять определенным условиям, в частности быть неотрицательной. Из ее свойств вытекает, что функции

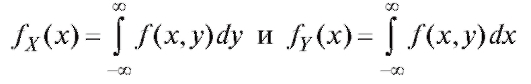
являются плотностями распределений случайных величин X и Y соответственно.

По аналогии с (7.41) непрерывные случайные величины X и Y называются независимыми, если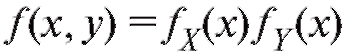при любых x и у.

Естественно, что также как ранее в случае (7.41), совместный закон распределения независимых величин X и Y взаимно однозначно определяется по их индивидуальным плотностям. Наконец, отметим, что определения ковариации, коэффициента корреляции и прямых средней квадратической регрессии не меняются, а их свойства сохраняются.

Пример 1. По закону распределения двумерного случайного вектора (X, Y), представленного табл. 7.9, найти:

а) математические ожидания и стандартные отклонения Xи Y;

б) корреляционный момент и коэффициент корреляции Xи Y;

Таблица 7.9

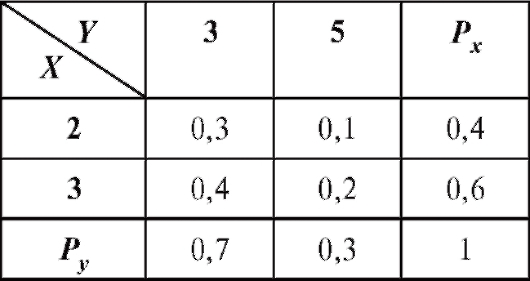
в) уравнение прямой средней квадратической (линейной) регрессии

Y на X. Решение.

а) Формулы (7.43):

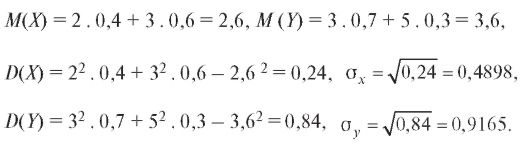
б) Формулы (7.44) и (7.45):

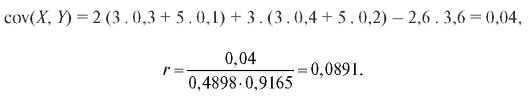
в) Формула (7.47) приводит к уравнению линейной регрессии

Самостоятельная работа

Дискретные случайные величины

1. Построить закон распределения и функцию распределения числа попаданий мячом в корзину при двух бросках, если вероятность попадания равна 0,4.

2. В партии из 10 деталей имеется 8 стандартных. Наугад отобраны 2 детали. Составить закон распределения стандартных деталей среди отобранных.

3. В партии из 6 деталей имеется 4 стандартных. Наугад отобраны 3 детали. Составить закон распределения дискретной случайной величины Х - числа стандартных деталей среди отобранных.

4. Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины Х - числа выпадений четного числа очков на обеих игральных костях.

5. В парии деталей 10 % нестандартных. Наугад отобраны 4 детали. Написать биномиальный закон распределения дискретной случайной величины Х - числа нестандартных деталей среди четырех отобранных.

Непрерывные случайные величины

6. Дана плотность распределения вероятности:

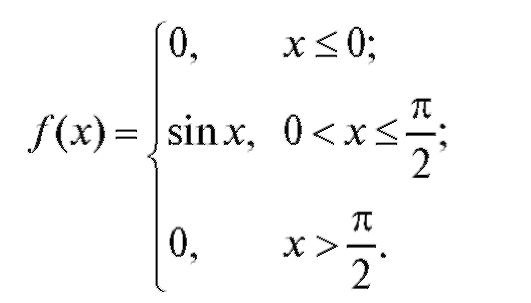
Найти F(x).

7. Дана плотность распределения вероятности:

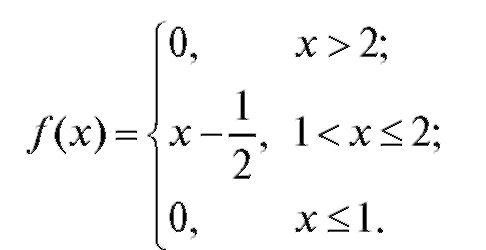
Найти F(x).

8. Дана плотность распределения вероятности:

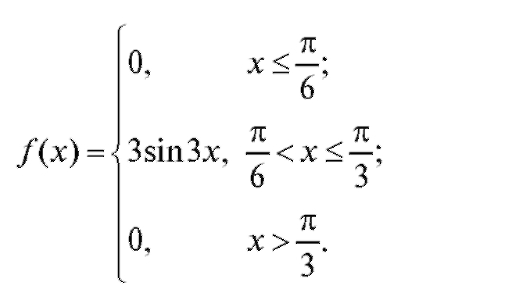
Найти F(x).

9. Дана плотность распределения случайной величины Х:

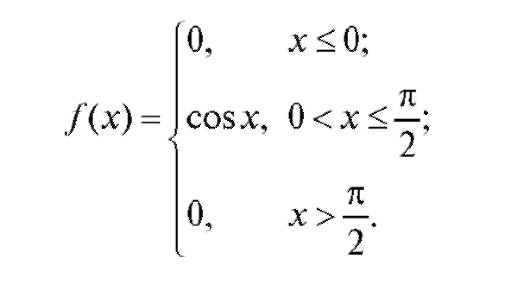
Найти функцию распределения F(x).

10. Непрерывная случайная величина Х задана плотностью вероятности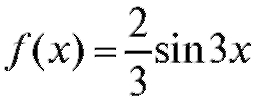в интервале, вне этого интервала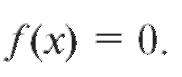Найти вероятность того, что Х примет значение, принадлежащее интервалу

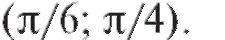
11. Случайная величина Х задана функцией распределения:

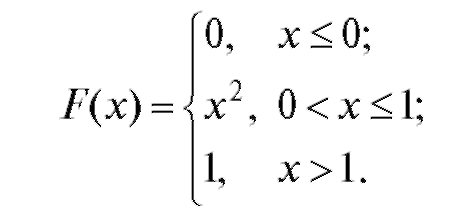
Найти вероятность того, что в результате четырех независимых испытаний величина Х ровно три раза примет значение, принадлежащее интервалу (0,25; 0,75).

Таблица 7.10

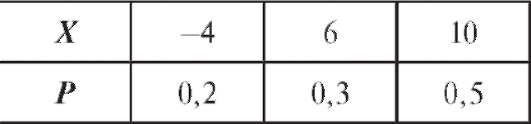
Числовые характеристики

12. Случайная величина Х задана законом распределения (табл. 7.10).

Найти математическое ожидание, дисперсию, среднее квадратичное отклонение, построить функцию распределения.

13. Найти дисперсию дискретной случайной величины Х - числа появлений события А в пяти независимых испытаниях, если вероятность появления события А в каждом испытании равна 0,2.

14. Дискретная случайная величина Х принимает только два возможных значения -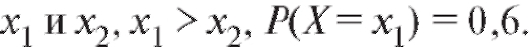Найти закон распределения величины Х, если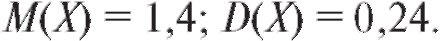

15. Случайная величина Х задана функцией плотности вероятности:

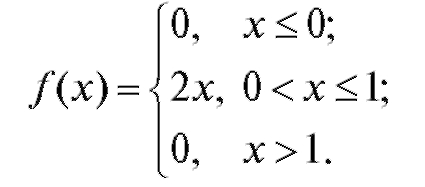
Найти математическое ожидание величины Х.

16. Случайная величина Х задана функцией плотности вероятности:

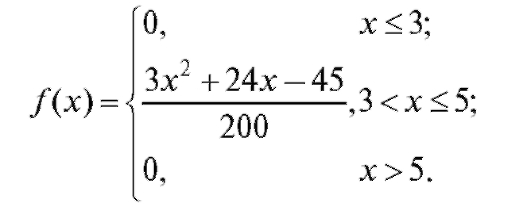
Найти математическое ожидание величины Х.

17. Случайная величина Х задана функцией плотности вероятности:

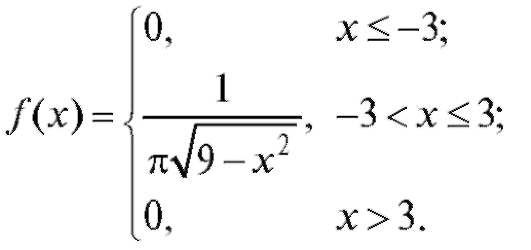
Найти дисперсию Х.

18. Плотность вероятности случайной величины Х, равномерно распределенной на

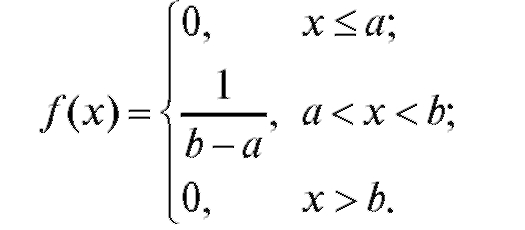
Найти:

1) функцию распределения F(x) и начертить ее график;

2) математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Х.

Нормальный закон

19. Масса взрослого животного некоторого вида является нормально распределенной случайной величиной со средним значением 100 кг и стандартным отклонением 8 кг. Наудачу выбирают взрослое животное. Найти вероятности того, что масса животного:

1) меньше 90 кг;

2) больше 110 кг;

3) находится в интервале от 95 до 105 кг;

4) находится в интервале от 97 до 112 кг.

20. Диастолическое давление крови выпускников некоторого училища является нормально распределенной случайной величиной со средним значением 80 мм и стандартным отклонением 5 мм. Измеряют давление крови у случайно выбранного выпускника. Определить вероятности того, что давление:

1) ниже 70 мм;

2) выше 85 мм;

3) выше 90 мм, но при дополнительном условии, что пациент выбран из числа тех, у кого на день проверки диастолическое давление оказалось выше 85 мм.

21. Предприятие выпускает стеклянные ампулы, средняя длина которых 100 мм и стандартное отклонение 1 мм. Ампула считается бракованной, если она короче 98 мм или длиннее 101 мм. Найти среднее число бракованных ампул среди наудачу взятых ста ампул.

22. В условиях задачи 21 найти интервал, симметричный относительно среднего значения длины ампул, в который попадает на удачу выбранная ампула с вероятностью не менее 0,96.

23. Определить среднеквадратичную ошибку весов, если систематических ошибок весы не имеют, а случайные распределения по нормальному закону и с вероятностью 0,9 не выходят за пределы ±20 мг.

24. Амперметр имеет систематическую ошибку 0,5 А и среднеквадратичную ошибку 0,1 А. Найти вероятность того, что ошибка измерения не превзойдет по абсолютной величине 0,5 А.

25. Весы имеют среднеквадратичную ошибку 60 мг, систематические ошибки отсутствуют. Сколько необходимо произвести взвешиваний, чтобы с вероятностью не менее 0,9 ошибка хотя бы не превосходила по абсолютной величине 7,5 мг?

26. Производят два независимых взвешивания на весах, имеющих среднеквадратичную ошибку 30 мг и систематическую ошибку +10 мг. Какова вероятность того, что обе ошибки измерения, имея разные знаки, по абсолютной величине превзойдут 10 мг?

27. Изделие считается высшего качества, если отклонение его длины от номинала не превосходит по абсолютной величине 3,45 мм. Случайное отклонение длины изделия от номинала подчиняется закону со среднеквадратичным отклонением в 3 мм. Систематические отклонения отсутствуют. Определить среднее число изделий высшего сорта, если изготовляют 4 изделия.

28. При большом числе измерений установлено, что 75 % ошибок:

1) не превосходит 1,25 мм;

2) не превосходит по абсолютной величине 1,25 мм. Заменяя частоты появления ошибок их вероятностями, определить в

обоих случаях среднеквадратичную ошибку измерения, если систематические ошибки отсутствуют.

29. Весы не имеют систематических ошибок. Случайная ошибка распределена по нормальному закону, причем σ = 10 мг. Сколько нужно произвести взвешиваний одного и того же предмета, чтобы с вероятностью не менее 0,98 средний арифметический результат имел ошибку в пределах ±3 мг?

30. Сколько нужно взять изделий по условию задачи 27, чтобы среди них с вероятностью не менее 0,97 было хотя бы одно изделие не высшего качества?

31. Средняя жирность данной партии молока 2,5 %. Отклонение жирности в отдельных пакетах от номинала составляет ±0,1 % с вероятностью 0,9973. Сколько пакетов молока нужно проверить, чтобы среди них был хотя бы один с молоком жирности менее 2,4 % с вероятностью не менее 0,9?

32. Рост взрослых мужчин является случайной величиной, распределенной по нормальному закону. Пусть ее математическое ожидание равно 175 см, а среднее квадратичное отклонение - 6 см. Определить вероятность того, что хотя бы один из наудачу выбранных мужчин будет иметь рост от 170 до 180 см.

33. Случайная величина Х распределена нормально с математическим ожиданием а = 25. Вероятность попадания в интервал (10; 15) равна 0,2. Чему равна вероятность попадания Х в интервал (35; 40)?