Глава 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

6.1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

При решении различных задач математики и физики, биологии и медицины довольно часто не удается сразу установить функциональную зависимость в виде формулы, связывающей переменные величины, которые описывают исследуемый процесс. Обычно приходится использовать уравнения, содержащие, кроме независимой переменной и неизвестной функции, еще и ее производные.

Определение. Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные различных порядков, называется дифференциальным.

Неизвестную функцию обычно обозначают y(x) или просто y, а ее производные - y', y" и т. д.

Возможны и другие обозначения, например: если y = x(t), то x"(t), x""(t) - ее производные, а t - независимая переменная.

Определение. Если функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным. Общий вид обыкновенного дифференциального уравнения:

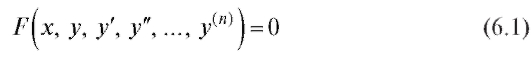
или

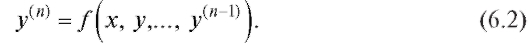
Функции F и f могут не содержать некоторых аргументов, но для того, чтобы уравнения были дифференциальными, существенно наличие производной.

Определение. Порядком дифференциального уравнения называется порядок старшей производной, входящей в него.

Например, x²y'- y = 0, y' + sinx = 0 - уравнения первого порядка, а y" + 2 y' + 5 y = x - уравнение второго порядка.

При решении дифференциальных уравнений используется операция интегрирования, что связано с появлением произвольной постоянной. Если действие интегрирования применяется n раз, то, очевидно, и в решении будет содержаться n произвольных постоянных.

6.2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Общий вид дифференциального уравнения первого порядка определяется выражением

Уравнение может не содержать в явном виде x и y, но обязательно содержит у'.

Если уравнение можно записать в виде

то получим дифференциальное уравнение первого порядка, разрешенное относительно производной.

Определение. Общим решением дифференциального уравнения первого порядка (6.3) (или (6.4)) является множество решений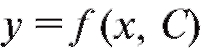, где С - произвольная постоянная.

График решения дифференциального уравнения называется интегральной кривой.

Придавая произвольной постоянной С различные значения, можно получить частные решения. На плоскости xOy общее решение представляет собой семейство интегральных кривых, соответствующих каждому частному решению.

Если задать точку A (x₀, y₀), через которую должна проходить интегральная кривая, то, как правило, из множества функций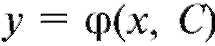 можно выделить одну - частное решение.

Определение. Частным решением дифференциального уравнения называется его решение, не содержащее произвольных постоянных.

Если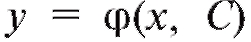является общим решением, тогда из условия

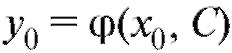можно найти постоянную С. Условие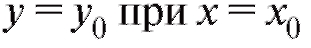называют начальным условием.

Задача нахождения частного решения дифференциального уравнения (6.3) или (6.4), удовлетворяющего начальному условию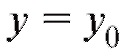при 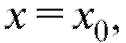называется задачей Коши. Всегда ли эта задача имеет решение? Ответ содержит следующая теорема.

Теорема Коши (теорема существования и единственности решения). Пусть в дифференциальном уравнении y' = f (x, y) функция f (x, y) и ее

частная производная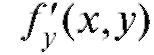 определены и непрерывны в некоторой

области D, содержащей точку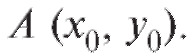Тогда в области D существует

единственное решение уравнения, удовлетворяющее начальному условию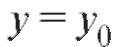при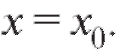

Теорема Коши утверждает, что при определенных условиях существует единственная интегральная кривая y = f (x), проходящая через точку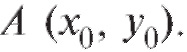Точки, в которых не выполняются условия теоремы

Коши, называются особыми. В этих точках терпит разрыв f (x, y) или.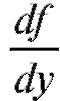

Через особую точку проходит либо несколько интегральных кривых, либо ни одной.

Определение. Если решение (6.3), (6.4) найдено в виде f (x, y, C) = 0, не разрешенным относительно у, то оно называется общим интегралом дифференциального уравнения.

Теорема Коши только гарантирует, что решение существует. Поскольку единого метода нахождения решения нет, мы будем рассматривать только некоторые типы дифференциальных уравнений первого порядка, интегрируемые в квадратурах.

Определение. Дифференциальное уравнение называется интегрируемым в квадратурах, если отыскание его решения сводится к интегрированию функций.

6.2.1. Дифференциальные уравнения первого порядка с разделяющимися переменными

Определение. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно представить в виде

Правая часть уравнения (6.5) представляет собой произведение двух функций, каждая из которых зависит только от одной переменной.

Например, уравнение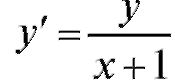является уравнением с разделяющи-

мися переменными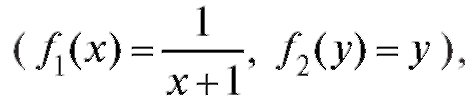а уравнение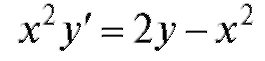

нельзя представить в виде (6.5).

Учитывая, что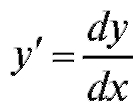, перепишем (6.5) в виде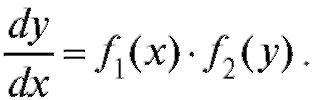

Из этого уравнения получим дифференциальное уравнение с разделенными переменными, в котором при дифференциалах стоят функции, зависящие лишь от соответствующей переменной:

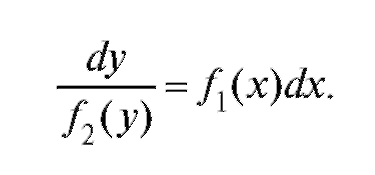
Интегрируя почленно, имеем

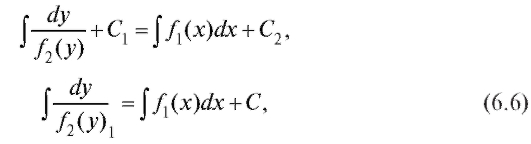
где C = C₂ - C ₁- произвольная постоянная. Выражение (6.6) представляет собой общий интеграл уравнения (6.5).

Разделив обе части уравнения (6.5) на ,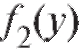, мы можем потерять те решения, при которых,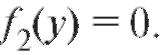Действительно, есл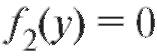ипри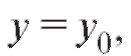

то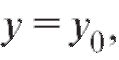очевидно, является решением уравнения (6.5).

Пример 1. Найти решение уравненияудовлетворяющее

условию: y = 6 при x = 2 (y (2) = 6).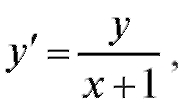

Решение. Заменим у'н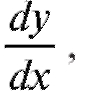атогда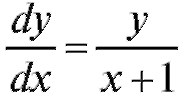. Умножим обе части на

dx, так как при дальнейшем интегрировании нельзя оставлять dx в знаменателе:

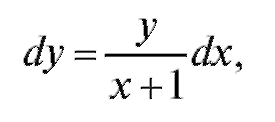
а затем, разделив обе части на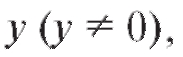получим уравнение,

которое можно проинтегрировать. Интегрируем: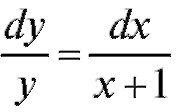

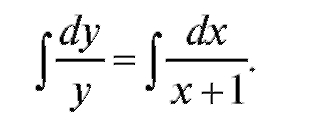
Тогда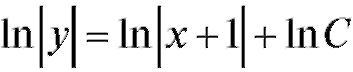; потенцируя, получим y = C • (x + 1) - об-

щее решение.

По начальным данным определяем произвольную постоянную, подставив их в общее решение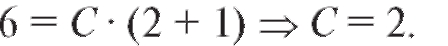

Окончательно получаем y = 2(x + 1) - частное решение. Рассмотрим еще несколько примеров решения уравнений с разделяющимися переменными.

Пример 2. Найти решение уравнения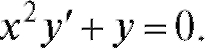

Решение. Учитывая, что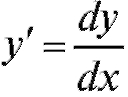, получим.

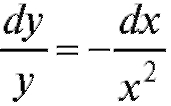Проинтегрировав обе части уравнения, будем иметь

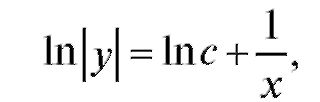
откуда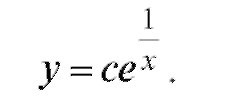

Пример 3. Найти решение уравнения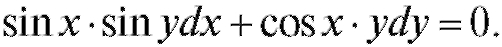 Решение. Делим обе части уравнения на те сомножители, которые зависят от переменной, не совпадающей с переменной под знаком дифференциала, т. е. на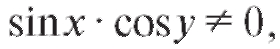и интегрируем. Тогда получим

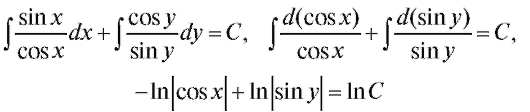
и, наконец,

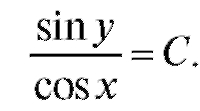
Пример 4. Найти решение уравнения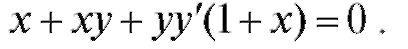

Решение. Зная, чтополучим. Разде-

лим переменные. Тогда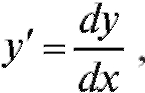

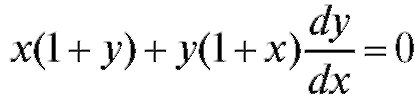
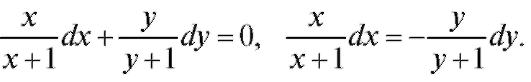
Интегрируя, получим

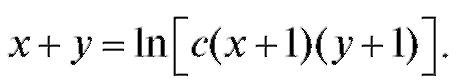
Замечание. В примерах 1 и 2 искомая функция y выражена явно (общее решение). В примерах 3 и 4 - неявно (общий интеграл). В дальнейшем форма решения оговариваться не будет.

Пример 5. Найти решение уравнения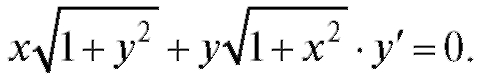 Решение.

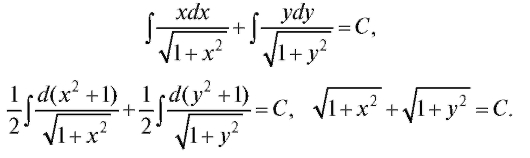
Пример 6. Найти решение уравнения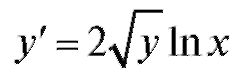, удовлетворяющее

условию y(e) = 1.

Решение. Запишем уравнение в виде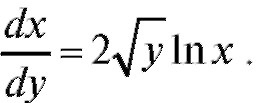

Умножая обе части уравнения на dx и на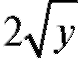, получим

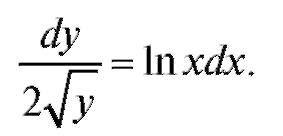
Интегрируя обе части уравнения (интеграл в правой части берется по частям), получим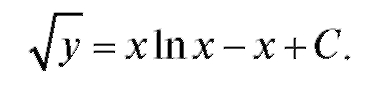

Но по условию y = 1 при x = e. Тогда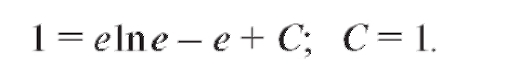

Подставим найденные значения С в общее решение:

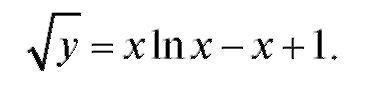
Полученное выражение называется частным решением дифференциального уравнения.

6.2.2. Однородные дифференциальные уравнения первого порядка

Определение. Дифференциальное уравнение первого порядка называется однородным, если его можно представить в виде

Приведем алгоритм решения однородного уравнения.

1. Вместо y введем новую функциюТогда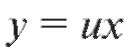и, следовательно,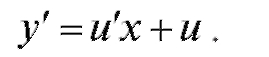

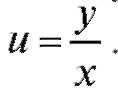
2. В терминах функции u уравнение (6.7) принимает вид

т. е. замена сводит однородное уравнение к уравнению с разделяющимися переменными.

3. Решая уравнение (6.8), находим сначала u, а затем y = ux.

Пример 1. Решить уравнение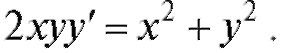 Решение. Запишем уравнение в виде

Производим подстановку: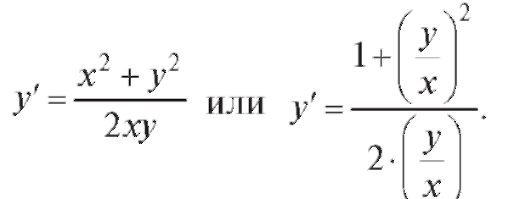 Тогда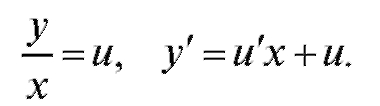

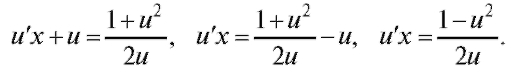
Заменим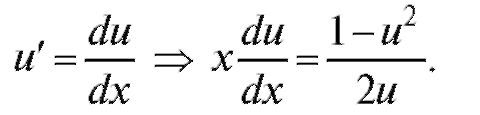

Умножим на dx: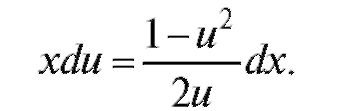 Разделим на x и н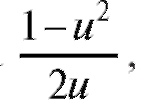атогда

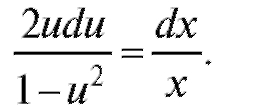
Проинтегрировав обе части уравнения по соответствующим переменным, будем иметь

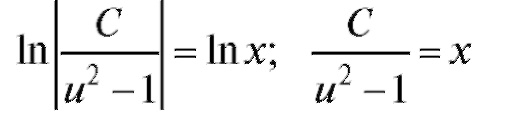
или, возвращаясь к старым переменным, окончательно получим

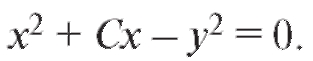
Пример 2. Решить уравнение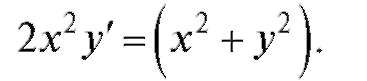 Решение. Пусть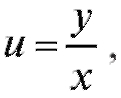тогда

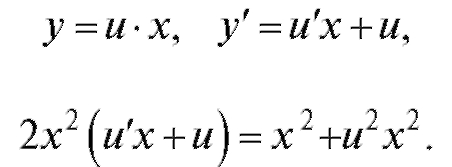
Поделим обе части уравнения на x²: 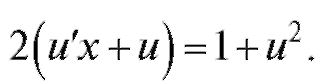Раскроем скобки и перегруппируем слагаемые:

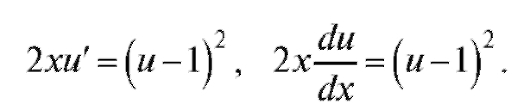
Далее, интегрируя, получим или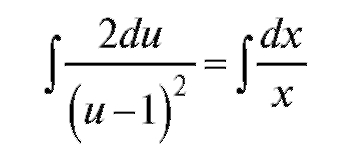

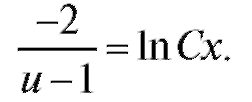
Переходя к старым переменным, придем к окончательному результату:

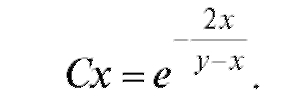
Пример 3. Найти решение уравнения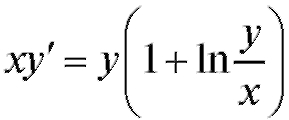 при условии

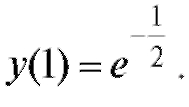
Решение. Выполняя стандартную замену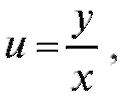получаем

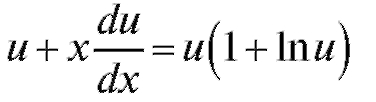
или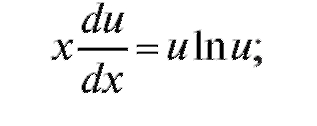

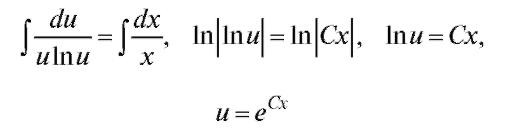
или

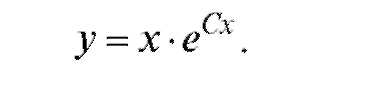
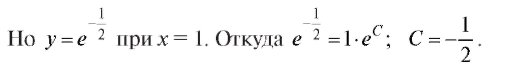
Значит, частное решение имеет вид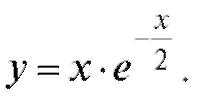 Пример 4. Найти решение уравнения

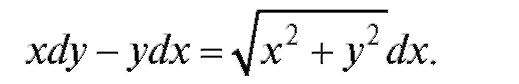
Решение.

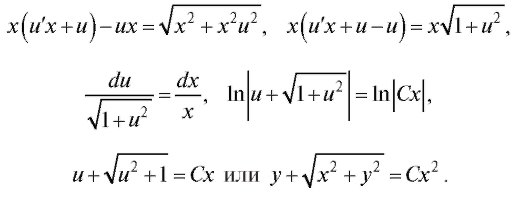
Пример 5. Найти решение уравнения 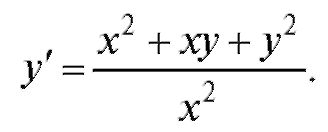Решение.

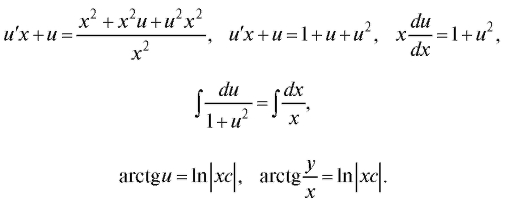
Самостоятельная работа

Найти решение дифференциальных уравнений с разделяющимися переменными (1-9).

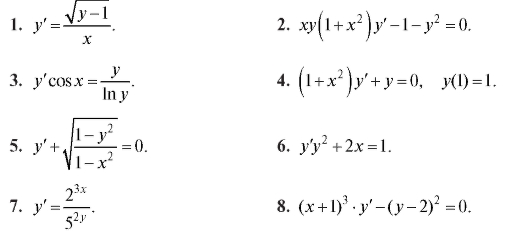
Найти решение однородных дифференциальных уравнений (9-18).

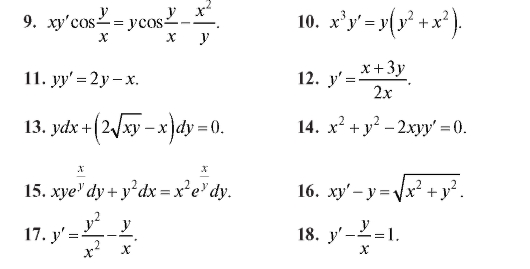
6.2.3. Некоторые приложения дифференциальных уравнений первого порядка

Задача о радиоактивном распаде

Скорость распада Ra (радия) в каждый момент времени пропорциональна его наличной массе. Найти закон радиоактивного распада Ra, если известно, что в начальный момент имелось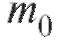Ra и период полураспада Ra равен 1590 лет.

Решение. Пусть в моментмасса Ra составляет x = x(t) г, причем 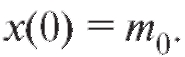Тогда скорость распада Ra равна

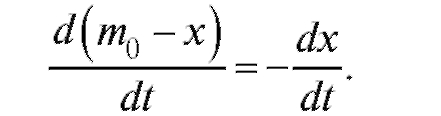
По условию задачи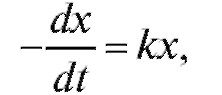

где k - коэффициент пропорциональности.

Разделяя в последнем уравнении переменные и интегрируя, получим

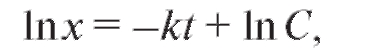
откуда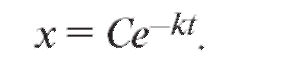

Для определения C используем начальное условие: при.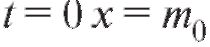

Тогда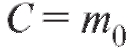и, значит,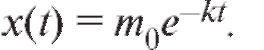

Коэффициент пропорциональности k определяем из дополнительного условия: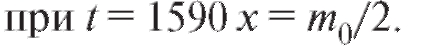

Имеем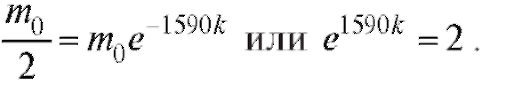

Отсюда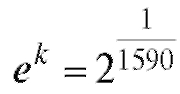и искомая формула

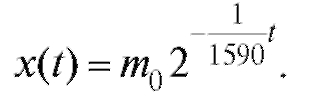
Задача о скорости размножения бактерий

Скорость размножения бактерий пропорциональна их количеству. В начальный момент имелось 100 бактерий. В течение 3 ч их число удвоилось. Найти зависимость количества бактерий от времени. Во сколько раз увеличится количество бактерий в течение 9 ч?

Решение. Пусть x - количество бактерий в момент t. Тогда, согласно условию,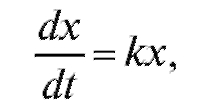

где k - коэффициент пропорциональности.

Отсюда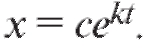Из условия известно, что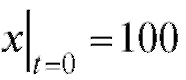. Значит,

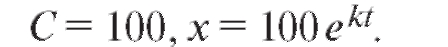
Из дополнительного условия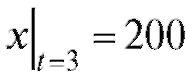. Тогда

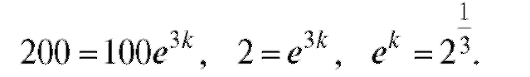
Искомая функция: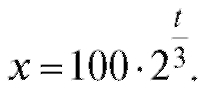

Значит, при t = 9 x = 800, т. е. в течение 9 ч количество бактерий увеличилось в 8 раз.

Задача об увеличении количества фермента

В культуре пивных дрожжей быстрота прироста действующего фермента пропорциональна его начальному количеству x. Первоначальное количество фермента a в течение часа удвоилось. Найти зависимость

x(t).

Решение. По условию дифференциальное уравнение процесса имеет вид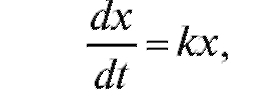

отсюда

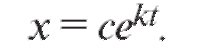
Но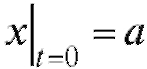. Значит, C = a и тогда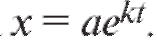

Известно также, что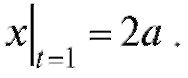

Следовательно,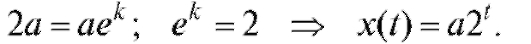

6.3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

6.3.1. Основные понятия

Определение. Дифференциальным уравнением второго порядка называется соотношение, связывающее независимую переменную, искомую функцию и ее первую и вторую производные.

В частных случаях в уравнении могут отсутствовать x, у или у'. Однако уравнение второго порядка обязательно должно содержать у". В общем случае дифференциальное уравнение второго порядка записывается в виде:

или, если это возможно, в виде, разрешенном относительно второй производной:

Как и в случае уравнения первого порядка, для уравнения второго порядка могут существовать общее и частное решения. Общее решение имеет вид:

Нахождение частного решения

при начальных условиях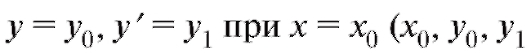- заданные

числа) называется задачей Коши. Геометрически это означает, что требуется найти интегральную кривую у = у (x), проходящую через заданную точку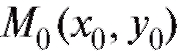и имеющую в этой точке касательную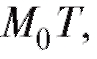которая об-

разует с положительным направлением оси Ox заданный угол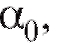т. е. 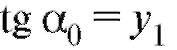(рис. 6.1). Задача Коши имеет единственное решение, если правая часть уравнения (6.10),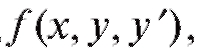непре-

рывна и имеет непрерывные частные производные по у, у' в некоторой окрестности начальной точки

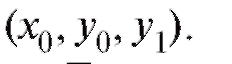
Для нахождения постоянных 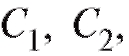входящих в частное решение, надо разрешить систему

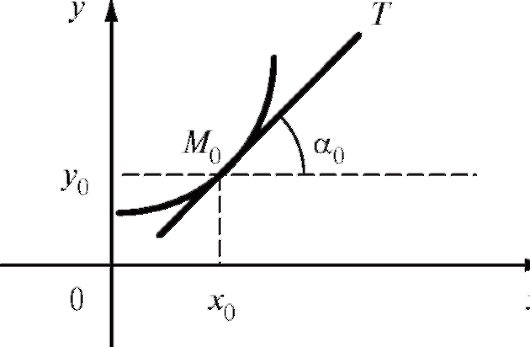
Рис. 6.1. Интегральная кривая

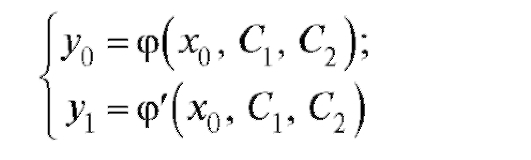
относительно произвольных постоянных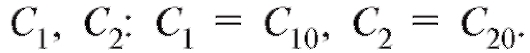 Подставляя найденные значения произвольных постоянных в общее решение (6.11), получим частное решение (6.14). Других решений с начальными данными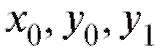нет.

Общее решение, записанное в виде, не разрешенном относительно искомой функции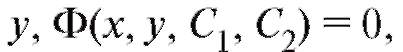называется общим интегралом.

6.3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Рассмотрим уравнение вида:

где p, q - действительные числа. Согласно п. 6.3.1 задача Коши для этого уравнения имеет единственное решение при любых начальных условиях.

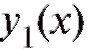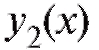Для нахождения общего решения уравнения (6.13) достаточно найти два линейно независимых его решенияи(функци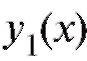ии 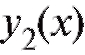- линейно независимы, если не имеет место тождество.

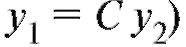Тогда общее решение, зависящее от аргумента x и двух произвольных постоянных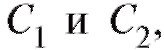получается как линейная комбинация:

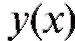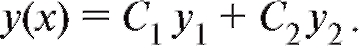
Процедура нахождения функци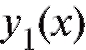йи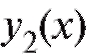описана в табл. 6.1.

Таблица 6.1. Таблица формул общего решения

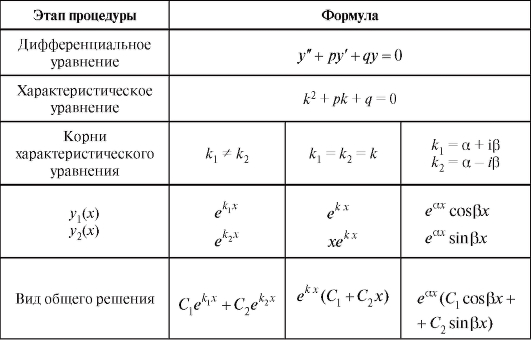
Из таблицы следует, что вид общего решения определяется корнями квадратного уравнения

которое называется характеристическим, а его корни k₁, k₂ - характеристическими числами.

Характеристическое уравнение может быть получено из исходного заменой у, у', у" на k⁰ = 1, k и k², соответственно, т. е. степень k совпадает с порядком производной у, если считать, что производная порядка 0 совпадает с самой функцией.

Уравнение (6.14) является уравнением второй степени и, следовательно, имеет два корня. Эти корни могут быть либо действительными различными 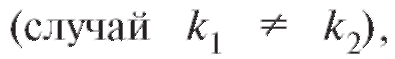либо действительными равными

(k₁ = k₂ = k), либо комплексными сопряженными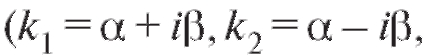

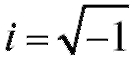- мнимая единица). Формальное решение уравнения (6.14) имеет вид

где .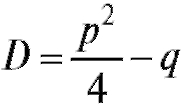

1. Корни характеристического уравнения действительные и различные,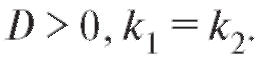

2. Корни характеристического уравнения действительные равные,

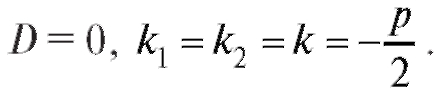
3. Корни характеристического уравнения комплексные сопряженные,

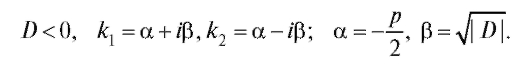
Покажем, что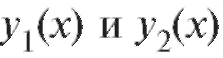являются решением дифференциального

уравнения (6.13), и, следовательно,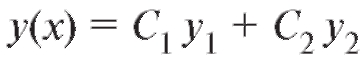представляет его

общее решение.

Рассмотрим 1-й случай.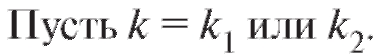Подставимв 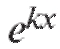уравне-

ние, учитывая, что .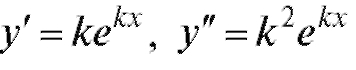

Тогда

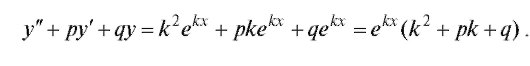
В силу (6.14) последний сомножитель равен нулю, откуда следует искомый результат.

Во 2-м случае достаточно проверить, что у₂ является решением. Действительно,

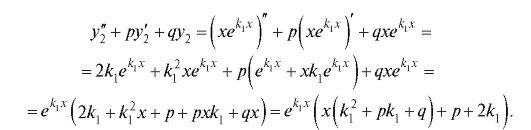
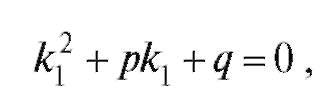так как 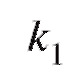- корень. По теореме Виета

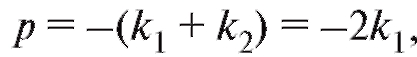поэтому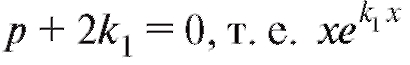- в самом деле яв-

ляется решением.

3-й случай проверяется аналогично.

Примеры.

1.

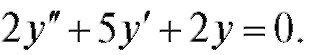
Составим характеристическое уравнение: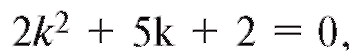откуда

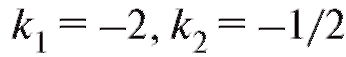и, следовательно,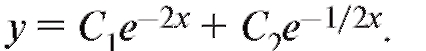

2.

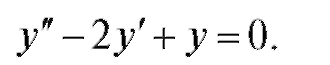
Этому дифференциальному уравнению соответствует характеристическое уравнение вида: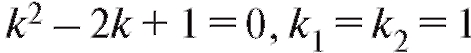и общее решение уравнения имеет вид:.

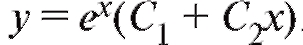3.

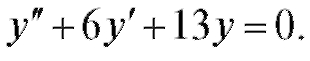
Характеристическое уравнение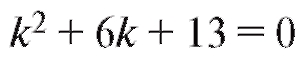будет иметь в данном

случае комплексно-сопряженные корни:

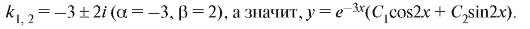
4.

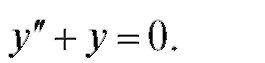
Характеристическое уравнение имеет вид: k² + 1 = 0 и его корни: 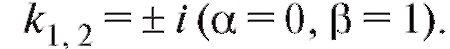Общее решение: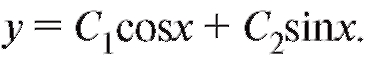

Самостоятельная работа

Решить уравнения (1-15).