Глава 5. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

5.1. ПОНЯТИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

К понятию определенного интеграла приводят разнообразные задачи математики, физики, химии и других точных наук, в том числе вычисление площадей плоских фигур, длин дуг, объема произведенной работы, количества вещества, образовавшегося в результате химической реакции. Далее рассмотрим некоторые из этих задач более подробно.

5.1.1. Вычисление площади криволинейной трапеции

Криволинейной трапецией будем называть плоскую фигуру, ограниченную осью Ox, графиком непрерывной функции y = f (x) и двумя вертикальными прямыми х = а и х = b. Далее для удобства будем считать

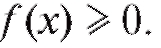
Пример. Фигура aABb, изображенная на рис. 5.1, является криволинейной трапецией. Чтобы вычислить площадь криволинейной трапеции, проделаем следующие действия. Сначала разделим основание трапеции [a; b] на n частичных интервалов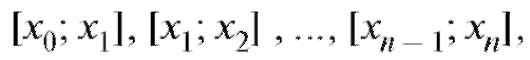 считая что

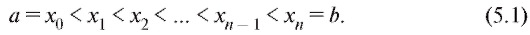
Проведем через точки разбиения прямые, параллельные оси Oy, тогда фигура aABb разделится на n элементарных криволинейных трапеций. Обозначим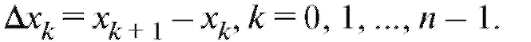

Вычислим площадь прямоугольника с основанием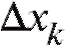и высотой

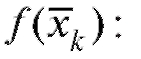
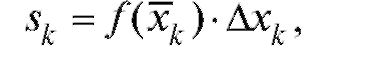
что приближенно равняется площади k-й элементарной криволинейной трапеции с тем же основанием (см. рис. 5.1). Учитывая, что площадь фигуры, составленной из нескольких непересекающихся фигур, равна сумме площадей этих фигур, получим

Эта сумма является приближением для искомой площади, причем чем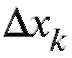меньше (а следовательно, n больше), тем это приближение, вообще говоря, точнее, т. е.

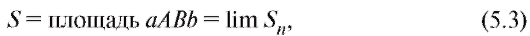
где переход к пределу совершается при условии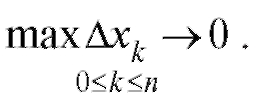

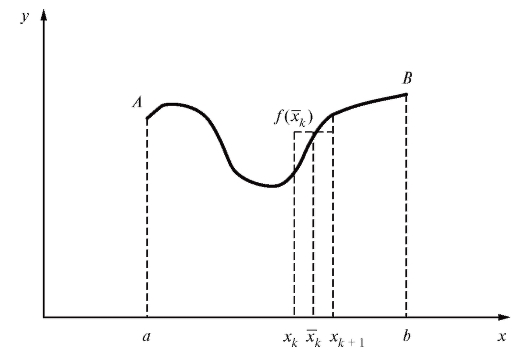
Рис. 5.1. Криволинейная трапеция

5.1.2. Определение пути

Предположим, что материальная точка совершает поступательное движение по прямой линии, причем в любой момент времени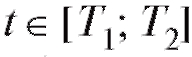 известна величина скорости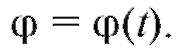Так же, как в (5.1), разобьем ин-

тервал [T₁; T₂] точками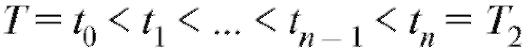на n непересекаю-

щихся промежутков.

Путь s, пройденный точкой за промежуток времени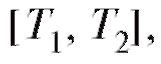опреде-

лим как

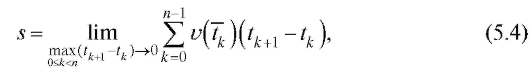
где, так же как и в (5.2), предполагается, что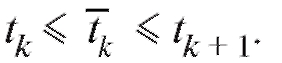

Такое определение пути выглядит вполне естественным, поскольку каждое слагаемое в (5.4) дает путь, который прошла бы точка за промежуток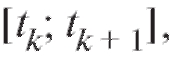двигаясь с постоянной скоростью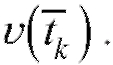

5.1.3. Количество вещества, образовавшегося в результате химической реакции

Предположим, что в результате химической реакции образуется некоторое вещество. Скорость химической реакции V=f (t), где t - время, предполагается известной величиной. Наша задача состоит в том, чтобы определить количество вещества, образовавшегося от момента времени t=a до момента времени t = b, где b > a. Разобьем временной промежуток [a; b] точками t = t₀ = a, t = t_x >t₀ t = t₂ > t₁ .... t = t_n = b. Таким образом, отрезок [a; b] разбивается на n отрезков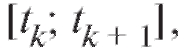где k = 0, 1,...... n - 1.

Если отрезок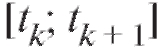достаточно мал, то можно пренебречь изменени-

ем скорости химической реакции на этом отрезке и приближенно считать, что скорость химической реакции на отрезке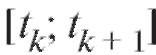постоянна и равна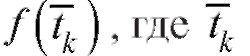- любая точка отрезка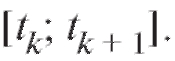Тогда масса вещества, образовавшегося в результате химической реакции за время от момента t = t_k до момента t = t_{k + 1}, приближенно находится по формуле

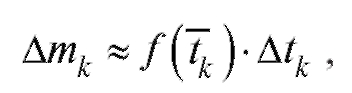
где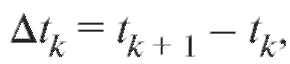а масса всего вещества, образовавшегося от момента

времени t = a до момента времени t = b, определяется приближенной

формулой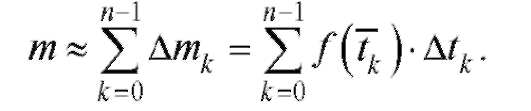

Эта формула тем точнее, чем короче промежутки времени At_k. Точный результат получается из приближенного путем перехода к пределу при условии max

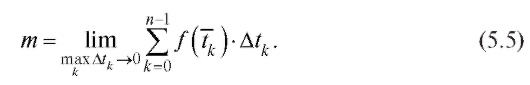
5.1.4. Определенный интеграл. Теорема существования

Рассмотренные примеры, если абстрагироваться от физического смысла переменных и их обозначений, приводят к одной и той же математической задаче: найти предел n-й интегральной суммы

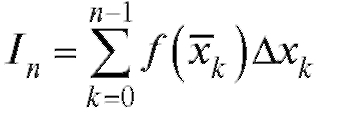(5.6)

при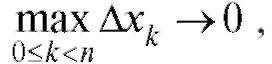где f (x) - функция непрерывная на промежутке [a; b],

а прочие обозначения такие же, как в (5.1) и (5.2). Другими словами:

1.Отрезок [a; b] разбиваем точками a = x0 < x1 < x2 <...< < x_{n - 1} < x_n = b на интервалы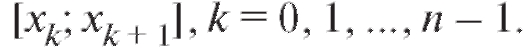

2.Берем произвольные точки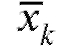из каждого интервала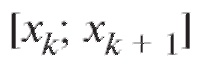и

вычисляем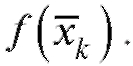

3. Составляем произведения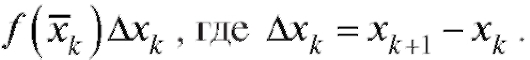

4. Вычисляем сумму этих произведений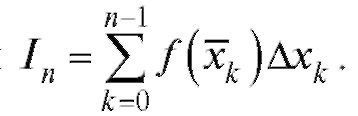

5. Находим предел I этой суммы при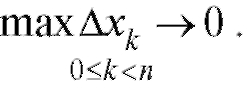

В общем случае такой предел называется определенным интегралом от функции f (x) в пределах от a до b и обозначается

(значокявляется стилизованной буквой S - первой буквы слова summa).

В (5.7), как ранее в неопределенном интеграле, функция f (x) называется подынтегральной функцией; f(x)dx - подынтегральным выражением; x - переменной интегрирования; a - нижним пределом интеграла; b - верхним пределом интеграла; [a; b] - промежутком интегрирования.

Определение. Определенным интегралом называется предел, к которому стремится n-я интегральная сумма (5.6) при стремлении к нулю длины наибольшего частичного интервала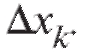

Обращаем внимание, что в обозначениях (5.7) площадь криволинейной трапеции 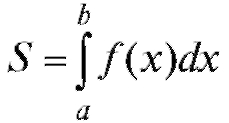, длина пути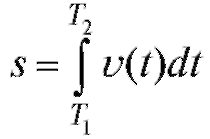, а масса вещества 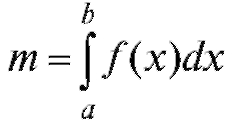(см. (5.2), (5.4) и (5.7)). Отсюда, в частности, следует, что

обозначение переменной интегрирования (т. е. x или t в данном случае) не играет роли и служит лишь интересам удобства.

Возникает естественный вопрос: для каких классов функций f (x) предел (5.6), посредством которого определяется интеграл (5.7), существует независимо от способа разбиения интервала [a; b] на частичные интервалы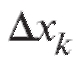и от выбора значений точек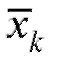внутри этих интервалов? Ответом является следующая теорема.

Теорема 5.1 (существования определенного интеграла). Если функция f (x) непрерывна в замкнутом интервале [a; b], то ее n-я интегральная сумма стремится к пределу при стремлении к нулю наибольшего частичного интервала. Этот предел не зависит от способа разбиения интервала интегрирования на частичные интервалы и от выбора в них промежуточных точек.

Итак, в классе непрерывных функций интеграл корректно

определен и всегда существует.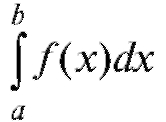

5.2. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Исходя из определения, можно установить следующие свойства определенного интеграла.

Свойство 1. Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых:

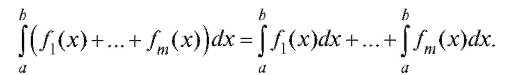
Свойство 2. Постоянный множитель подынтегральной функции можно выносить за символ интеграла:

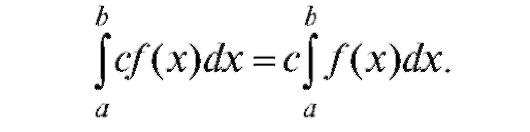
В частности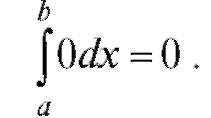

Свойство 3. Если верхний и нижний пределы интеграла поменять местами, то интеграл изменит знак:

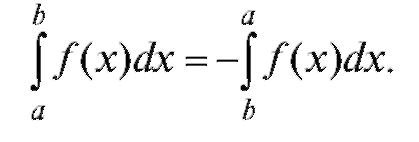
В частности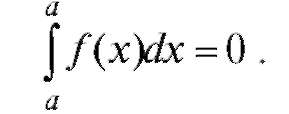

Свойство 4. Если интервал интегрирования [a; b] разбить на две части [a; с] и [с; b], то

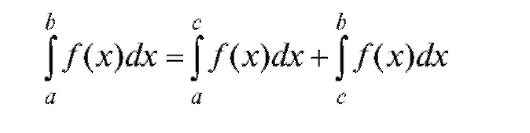
(свойство аддитивности определенного интеграла).

Свойство 5. Если подынтегральная функция в интервале интегрирования не меняет знака, то интеграл представляет собой число того же знака, что и функция. В частности, если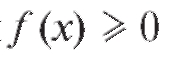в интервале [a; b], где

a < b, то

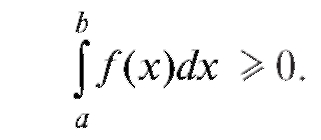
Свойство 6. Геометрический смысл определенного интеграла. В соответствии с п.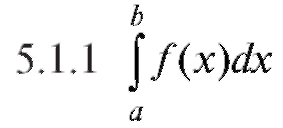 равен площади под графиком

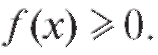В случае, если f (x) на [a; b] имеет разные знаки (рис. 5.2), общая площадь будет вычисляться по формуле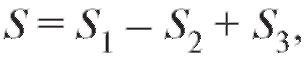или

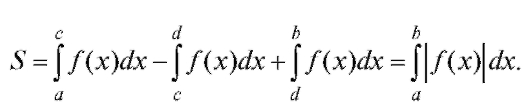
Свойство 7. Если в интервале [ a ; b ], гдето

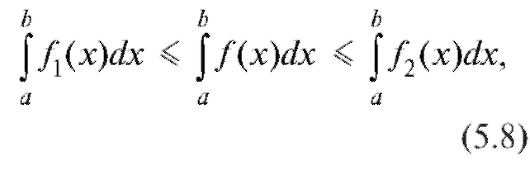
т. е. неравенства можно интегрировать.

В частности, если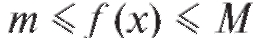 на [a; b], то

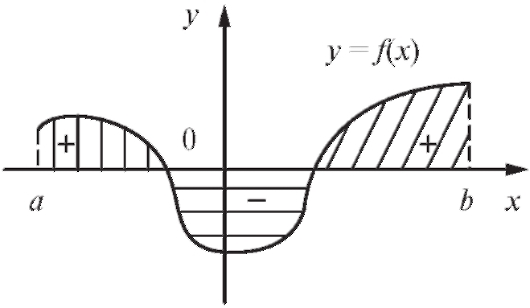
Рис. 5.2. Геометрический смысл определенного интеграла

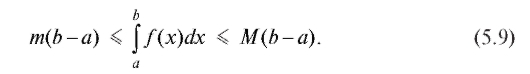
Заметим, что в (5.9) можно положить.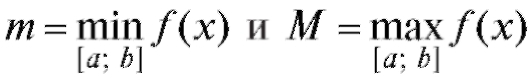

Соотношение (5.9) имеет следующую геометрическую интерпретацию: площадь криволинейной трапеции заключена между площадями прямоугольников, каждый из которых имеет основание, равное основанию трапеции, и высоты, равные соответственно наименьшей и наибольшей ординате трапеции (рис. 5.3). Теорема 5.2 (о среднем). Внутри интервала [a; b] существует по крайней мере одно значение x = с, при котором

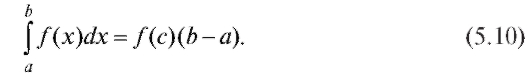
Доказательство. Из соотношения (5.9) пр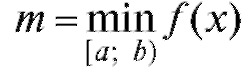и и

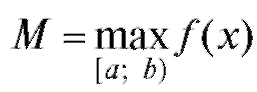следует, что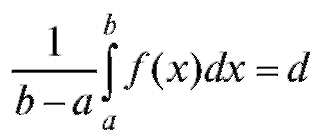, где d - некоторое число из

интервала [m; М]. Известно, однако, что каждая непрерывная функция обязательно, по крайней мере единожды, принимает любое значение между m и М, т. е. f (с) = d при некотором с,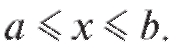

Определение. Величина f (с) называется средним значением функции f (x) на интервале [a; b].

Геометрически теорема о среднем означает, что площадь криволинейной трапеции равна площади прямоугольника, основание которого совпадает с основанием трапеции, а высота равна значению кривой, ограничивающей эту трапецию, в некоторой промежуточной точке. Продолжим изучение свойств определенного интеграла.

Дляположим. 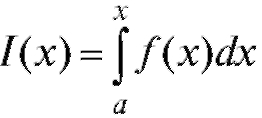Таким образом, нами введена

функция верхнего предела интеграла, заданная на интервале [a; b].

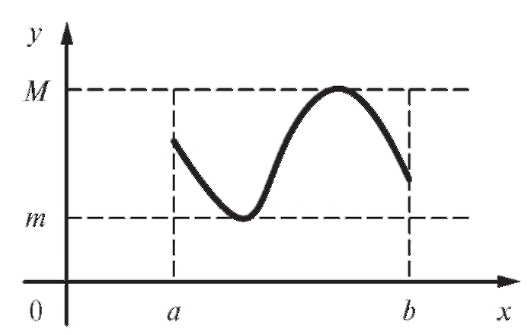
Рис. 5.3. Геометрический смысл оценки (5.9)

Более строго было бы употреблять запись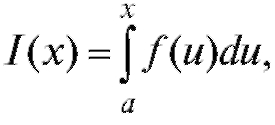однако до-

статочно просто помнить о различном смысле переменных интегрирования и верхнего предела.

Свойство 8. Производная интеграла по его верхнему пределу равна подынтегральной функции, вычисленной на верхнем пределе:

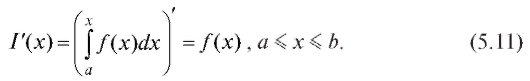
Другими словами, интеграл с переменным верхним пределом суть первообразная для подынтегральной функции.

Доказательство. Из свойства 4 и теоремы о среднем следует

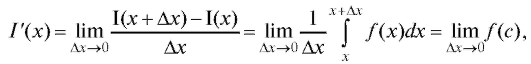
но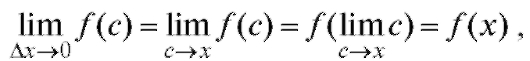поскольку f (x) непрерывна на

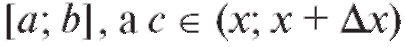и, следовательно,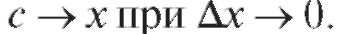

5.3. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА

Непосредственное вычисление интеграла как предела соответствующих интегральных сумм (см. формулу (5.6)) затруднительно, да и не требуется, поскольку для этой цели можно воспользоваться следующей теоремой.

Теорема 5.3. Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интеграла:

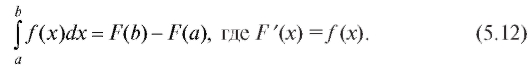
Равенство (5.12) называется формулой Ньютона-Лейбница. Доказательство. В соответствии с равенством (5.11) функция

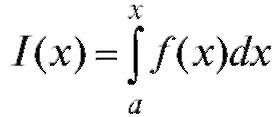является первообразной от функции f (x) и поэтому имеет вид F (x) + C, где F (x) - некоторая первообразная от f (x), а С - опре-

деленная постоянная, т. е. I (x) = F (x) + C. По свойству (3) 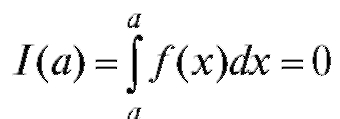, откуда I (a) = 0 = F (a) + C, или С = - F (a). Другими

словами,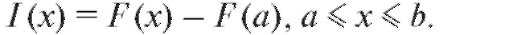

При x = b отсюда получаем (5.12). Теорема доказана. Разность значений функции часто записывают так:

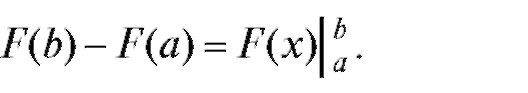(5.13)

В случае использования обозначения (5.13) формуле Ньютона- Лейбница можно придать вид:

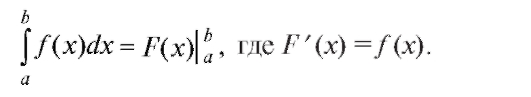(5.14)

Формула Ньютона-Лейбница дает нам альтернативный способ вычисления определенных интегралов. Она позволяет находить их по формуле:

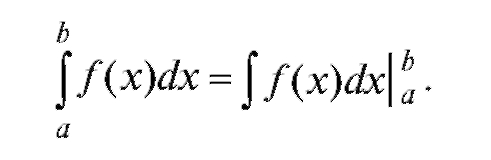(5.15)

В качестве иллюстрации приведем несколько примеров:

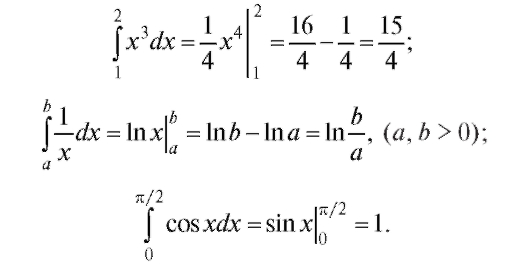
5.4. МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 5.4.1. Метод замены переменной

Если в интервале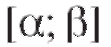функции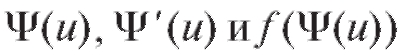непрерывны и

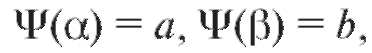то

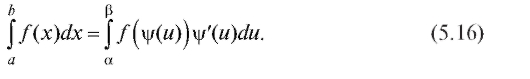
Равенство (5.16) следует из соотношения (5.15) и формулы замены переменной в неопределенном интеграле (принимается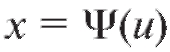). От-

метим, что новые пределы интегрирования а и р являются корнями уравнений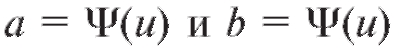соответственно. При этом желательно

(хотя и не обязательно) в случае, когда уравнения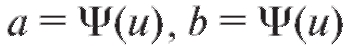ре-

шаются неоднозначно, брать наименьший интервал изменения и. Например, если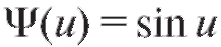, a = 0,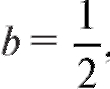то предпочтительнее выбор,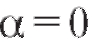

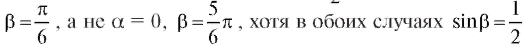(см. пример 1 далее).

Часто замена переменной в интеграле производится по формуле и = g (x), выражающей новую переменную через заданную (а не наоборот, как в (5.16)). Тогда новые пределы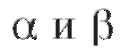вычисляются непосредственно по формулам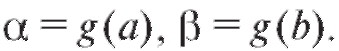Заметим, что при такой замене переменных требуется, чтобы функция g (x) была обратимой в интервале [a; b]: для этого достаточно, чтобы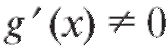при всех .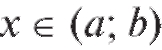. Примеры.

1.

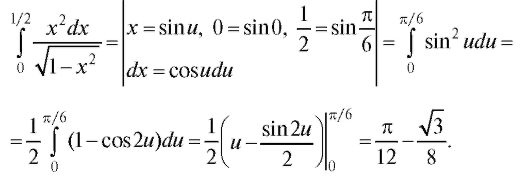
2.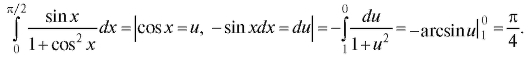 3.

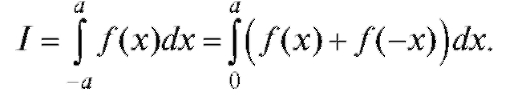
Действительно,

где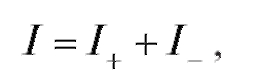 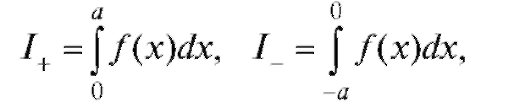но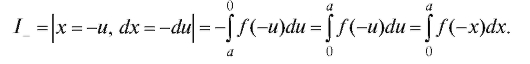

Следствием доказанного равенства является полезная формула

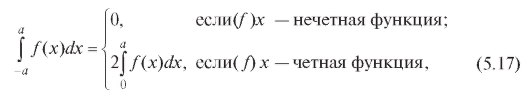
позволяющая находить значения некоторых определенных интегралов без вычислений.

Самостоятельная работа

Вычислить (1-20).

5.4.2. Метод интегрирования по частям

Справедливо равенство

где u и V - функции независимой переменной. Доказательство. Имеем по (5.15)

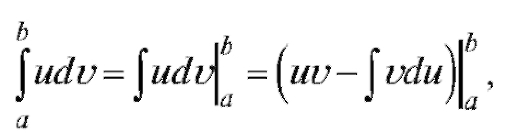
откуда следует (5.18).

В качестве примера использования формулы (5.18) вычислим интеграл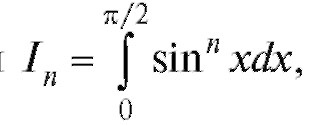где n - натуральное число. При n = 0 или n = 1 интеграл легко берется:

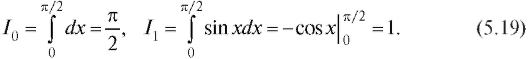
ПустьПоложим 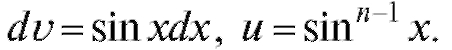Тогда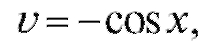

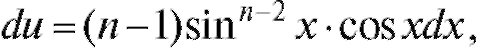
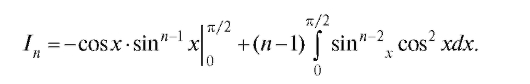
Первое слагаемое здесь равно нулю. Заменяя во втором слагаемом множитель cos²x на 1 - sin²x, получим

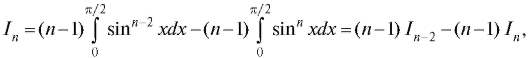
откуда следует, что

Пользуясь этой рекуррентной формулой, мы в состоянии понизить показатель степени n до 0 (если n - четное число) или до 1 (при нечетном n). С учетом (5.19) задача решается до конца. Так,

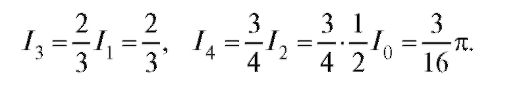
Примеры.

Самостоятельная работа

Вычислить интегралы (1-17).

5.5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

5.5.1. Несобственные интегралы с бесконечными пределами интегрирования

Понятие определенного интеграла было установлено для функции f (x), непрерывной на конечном интервале [a; b]. Пусть теперь функция f (x) непрерывна на бесконечном интервале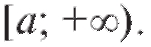

Определение. Несобственным интегралом от функции f (x) на интервале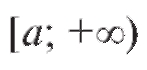называется предел интеграла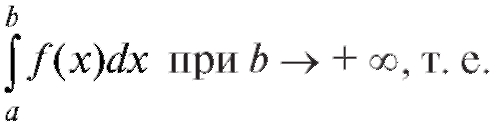

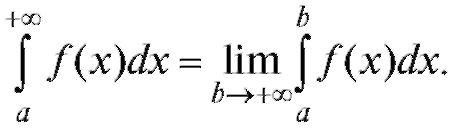
Если этот предел существует, то несобственный интеграл называется сходящимся, а если не существует (т. е. стремится к бесконечности или колеблется), то расходящимся.

Аналогично определяются несобственные интегралы и для прочих бесконечных интервалов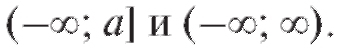

Обозначив через F (x) первообразную от функции f (x), условно можно записать

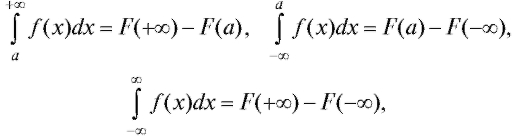
понимая под символомпредел, к которому стремится F (x) при

Примеры.

1.

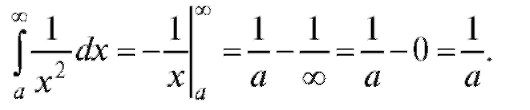
2.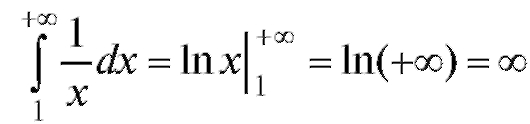 - интеграл расходится.

Заметим, что несобственный интеграл можно, как и ранее, интерпретировать как площадь соответствующей бесконечной криволинейной трапеции. Таким образом, в первом примере площадь

фигуры, расположенная между кривой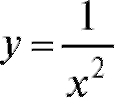и осью Ox на интер-

вале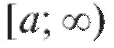(рис. 5.4), равна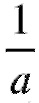, а во

втором - не существует (равна бесконечности).

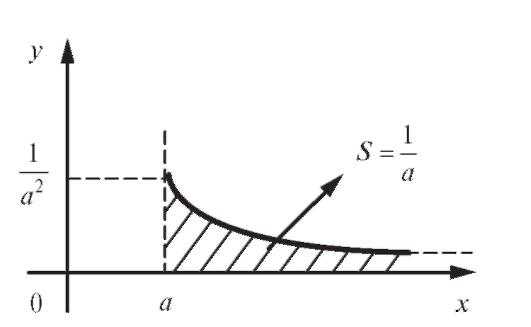
Рис. 5.4. Площадь бесконечной криволинейной трапеции

4. 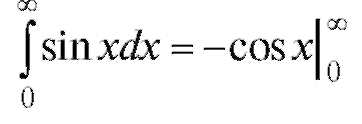не имеет предела (т. е. интеграл расходится).

Самостоятельная работа

Установить сходимость или расходимость несобственных интегралов (1-6).

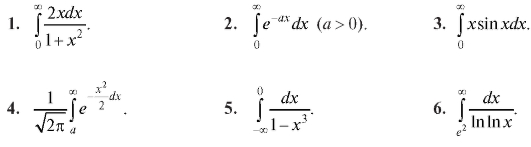
5.5.2. Интегралы от разрывных функций

Если в интервале (конечном или бесконечном) интегрирования функция f (x) имеет некоторое число разрывов первого рода, то интеграл определяется как сумма интегралов по частичным интервалам, на которые точки разрыва разбивают основной промежуток интегрирования.

Другими словами, если функция f (x) определена в интервале [a; b] и имеет в нем точки разрыва, то

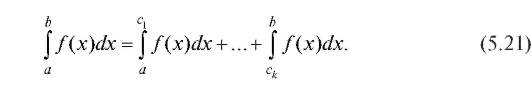
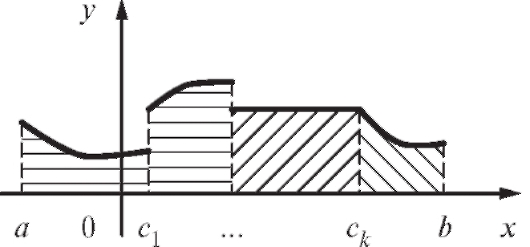
Рис. 5.5. Площадь криволинейной трапеции, соответствующей функции y = f (x) с конечным числом точек разрыва первого рода

Последняя формула имеет очевидную геометрическую иллюстрацию (рис. 5.5).

Если функция f (x) в интервале интегрирования претерпевает один или несколько разрывов второго рода, то интеграл определяется следующим образом.

Определение. Пусть функция f (x) непрерывна в интервале [a; b) и при х - b, x < b не имеет конечного предела. Несобственным ин-

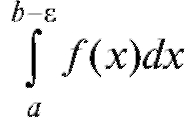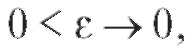тегралом от функции f (x) в интервале [a; b) называется предел интеграла прит. е.

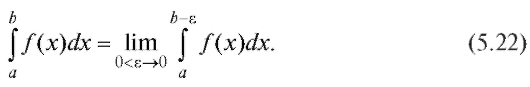
Если предел существует, то несобственный интеграл называется сходящимся, иначе - расходящимся.

Аналогично определяется несобственный интеграл от функции f (x), претерпевающей разрыв лишь в левом конце интервала интегрирования:

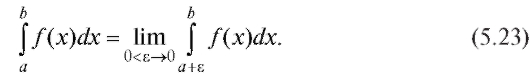
В случае, когда функция f (x) непрерывна в интервале [a; b) и имеет разрывы второго рода в его обоих концах, полагаем

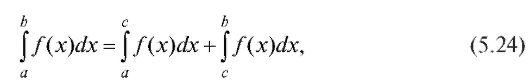
где c - любая точка из интервала (а; Ъ).

Если же функция f (x) имеет разрывы второго рода в некоторых промежуточных точкахто пользуемся равенством

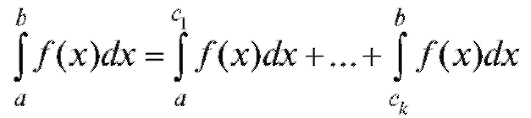
и вычисляем слагаемые в правой части по формулам (5.22)-(5.24) соответственно.

Пример 1. Определить, сходится ли интеграл

Решение. Если n < 1, то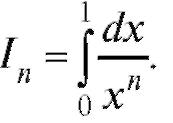

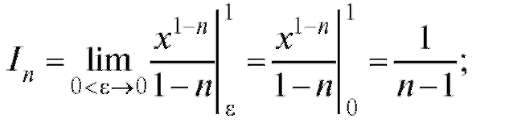
если n = 1, то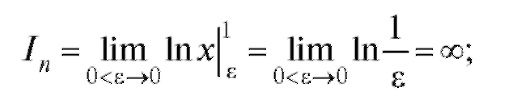 если n > 1, то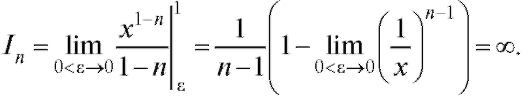

Таким образом, несобственный интеграл I_n сходится при n < 1 и расходится, если

Пример 2. Определить, сходится ли интеграл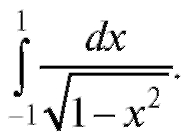 Решение.

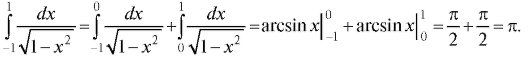
Интеграл сходится.

Пример 3. Определить, сходится ли интеграл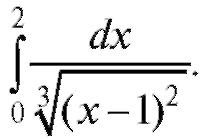 Решение.

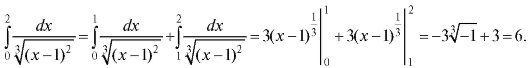
Интеграл сходится.

Самостоятельная работа

Определить, сходятся ли интегралы (1-3).

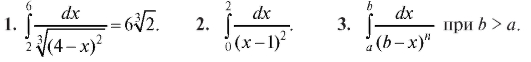
5.6. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

Рассмотрим приложения определенных интегралов для вычисления площади, длины дуги и объема тела вращения в зависимости от формы задания кривых.

5.6.1. Вычисление площади плоской фигуры

Если плоская фигура ограничена прямыми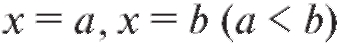и кри-

выми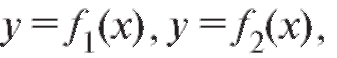причем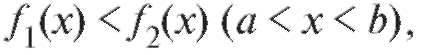то ее площадь вы-

числяется по формуле:

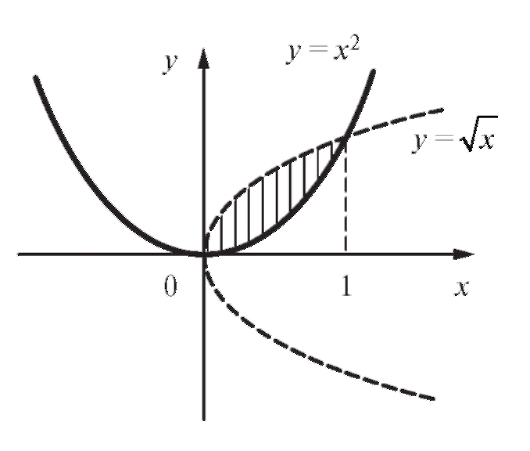
Рис. 5.6. Площадь, ограниченная двумя параболами

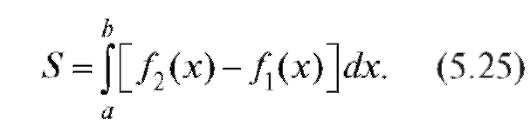
В частном случае, когда плоская фигура ограничена снизу осью Ох, формула (5.25) несколько упрощается:

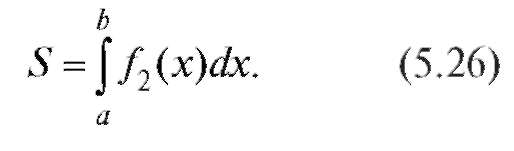
Пример 1. Вычислить площадь фигуры, ограниченной кривыми

(рис. 5.6)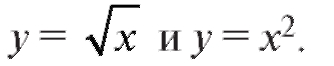

Решение. Находим точки пере-

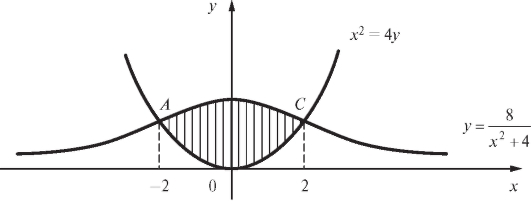
Рис. 5.7. Площадь между параболой и локоном Аньези

Решение. Найдем абсциссы точек A и C пересечения кривых. Для этого исключим y из системы уравнений:

сечения кривых: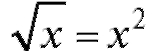, следовательно, x = x⁴, откуда x₁ = 0, x₂ = 1. По

формуле (5.25) имеем:

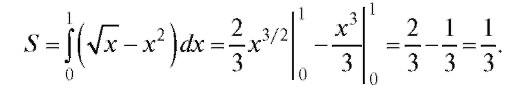
Пример 2. Найти площадь фигуры, заключенной между параболой x² = 4y и локоном Аньези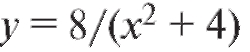(рис. 5.7).

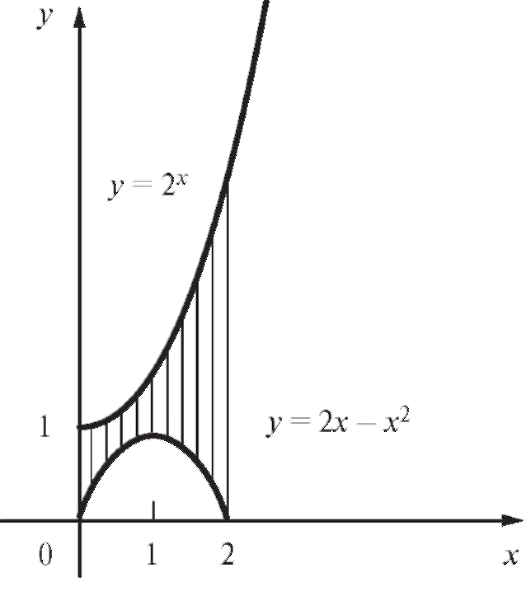
Рис. 5.8. Площадь между параболой и показательной кривой

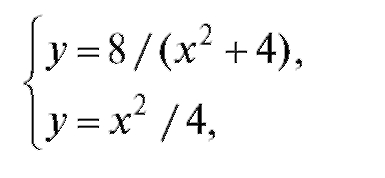
откуда 8/(x² + 4) = x²/4, или

x⁴ + 4x² - 32 = 0.

Действительными корнями этого уравнения являются точки x₁ = -2 и x₂ = 2. Функция на отрезке [-2; 2] (в чем можно убедиться прямым подсчетом значений этих функций в любой точке внутри отрезка, например в точке x = 0). Следовательно, по формуле (5.25) получим:

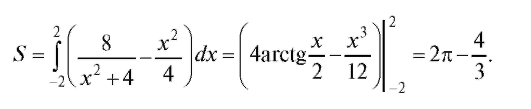
Пример 3. Вычислить площадь фигуры, ограниченной прямыми x = 0, x = 2 и кривыми y = 2^x, y = 2x - x² (рис. 5.8).

Решение. Так как максимум функции y = 2x - x² достигается в точке x = 1 и равен 1, а функция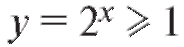на отрезке [0; 2], то

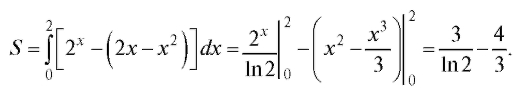
5.6.2. Вычисление длины дуги плоской кривой

Пусть некоторая кривая задана уравнением y = f (x). Длина дуги AB этой кривой, заключенная между вертикальными прямыми x = а и x = Ъ, находится по формуле:

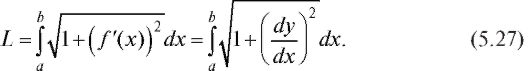
Пример 1. Определить длину окружности x² + y² = r². Решение. Вычислим сначала длину четвертой части окружности, лежащей в первом квадранте. Тогда уравнение дуги AB будет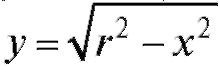, откуда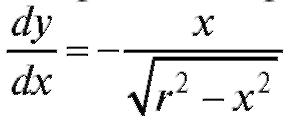,следовательно,

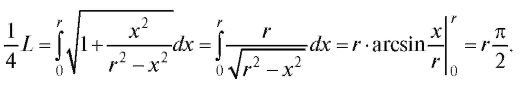
Длина всей окружности L = 2πr.

Пример 2. Найти длину дуги кривой y² = x³ от x = 0 до x = 1 (y > 0). Решение. Дифференцируя уравнение кривой, найдем y' = (3/2)x^1/2, откуда

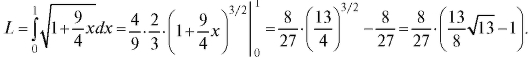
Пример 3. Вычислить длину дуги кривой y = ln cos x, заключенной между точками с абсциссами x = 0, x = π/4.

Решение. Так как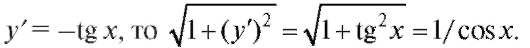 Следовательно,

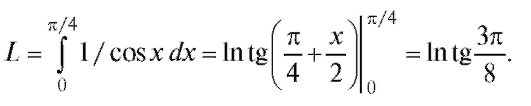
5.6.3. Вычисление объема тела вращения

Пусть дана криволинейная трапеция, ограниченная кривой y = f (x), осью Ox и прямыми x = a, x = b. Вращая эту фигуру вокруг оси Ox, получим тело вращения. Для вычисления объема тела вращения применяется формула:

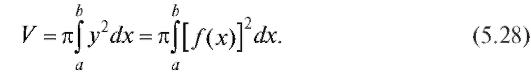
Рассмотрим примеры.

Пример 1. Вычислить объем тела, образуемого вращением вокруг оси

Ox фигуры, ограниченной линиями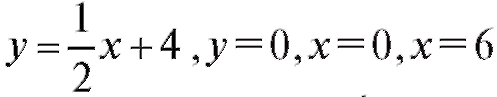(рис. 5.9).

Решение. В первую очередь следует построить эту фигуру и изобразить на том же чертеже тело вращения. В данной задаче a = 0, b = 6,

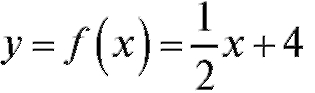. По формуле (5.28) находим

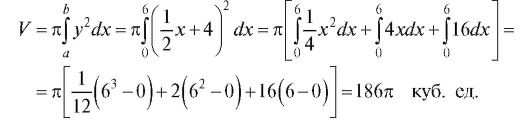
Результат можно проверить по формуле объема усеченного конуса:

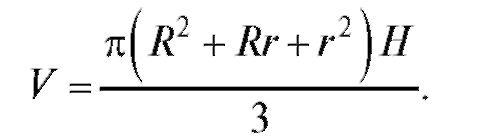
Проверку рекомендуется выполнить самостоятельно.

Пример 2. Найти объем тела, образуемого вращением цепной линии

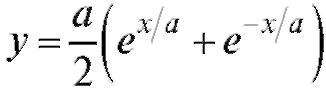вокруг оси Ox на участке от x = 0 до x = b (рис. 5.10).

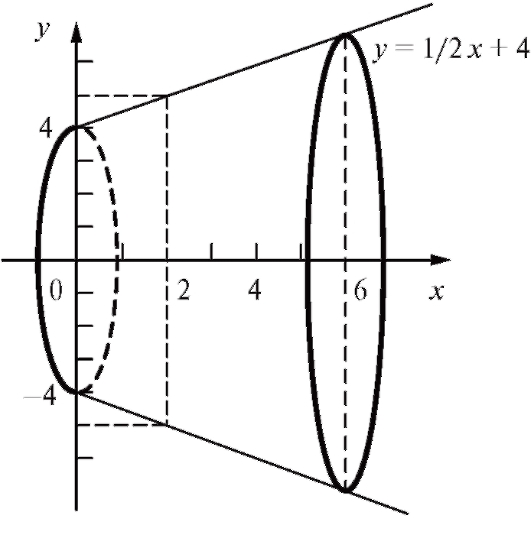
Рис. 5.9. Объем тела, образованного вращением линии y = 1/2 x + 4 вокруг оси Ох

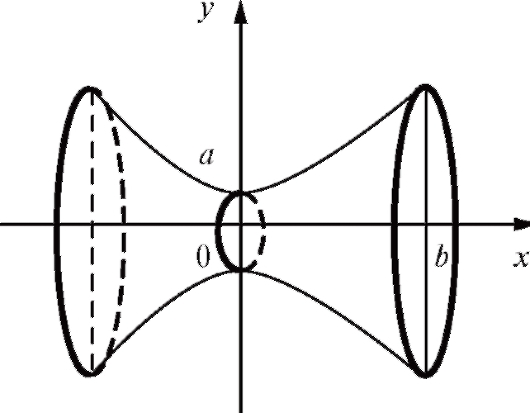
Рис. 5.10. Объем тела, образованного вращением вокруг оси Ох цепной линии

Решение.

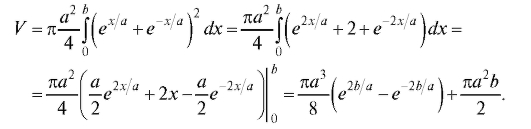
Пример 3. Фигура, ограниченная дугой синусоиды y = sin x, осью ординат и прямой y =1, вращается вокруг оси Oy (рис. 5.11).

Определить объем V получающегося тела вращения.

Решение. Обратная функция x = arcsin y рассматривается на отрезке [0; 1]. Поэтому

Рис. 5.11. Объем тела, образованного вращением вокруг Oy дуги синусоиды

Таблица 5.1

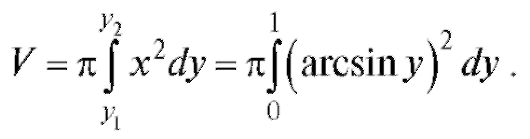
Применим подстановку arcsin y = t. Отсюда следует, что если y = 0, то t = 0, а если y = 1, то t =π/2 (табл. 5.1).

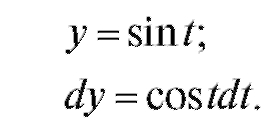
Значит, 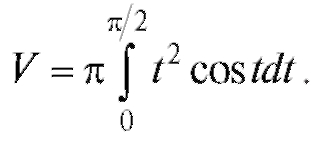Интегрируя по частям, получим V =

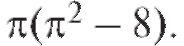
Самостоятельная работа

1. Найти площадь, заключенную между параболой y = x² - 2x + 2, касательной к ней в точке М(3; 5) и осью ординат.

2. Вычислить площадь фигуры, ограниченной линиями y = (x - 4)², y = 16 - x² и осью Ох.

3. Вычислить площадь фигуры, ограниченной параболами y = x², x = (3/4)y² + 1.

4. Вычислить площадь частей эллипса x² + 4y² = 8, отсеченных гиперболой x² - 3y² = 1.

5. Вычислить площадь фигуры, ограниченной замкнутой кривой

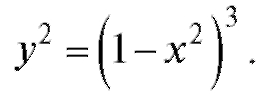
6. Вычислить площадь фигуры, ограниченной кривой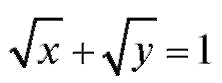и прямой x + y = 1.

7. Вычислить площадь фигуры, ограниченной кривой y = x², осью Ох и прямыми х = 1 и х = 3.

8. Вычислить площадь фигуры, ограниченной кривой y = 4x² - x³ и осью Ох.

9. Вычислить площадь фигуры, ограниченной линиями y = 4 - x², y = x + 2.

10. Вычислить длину дуги кривой y = x²/2 - 1, отсеченной осью Ох.

11. Вычислить длину дуги кривой y = ln(2cos x) между соседними точками пересечения с осью Ох.