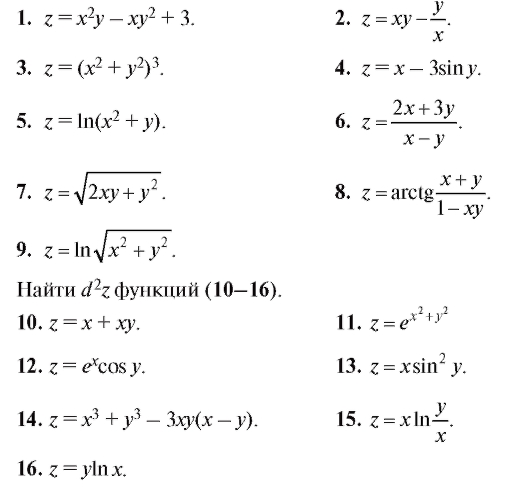Математика : учебник / И. В. Павлушков, Л. В. Розовский, И. А. Наркевич. - 2013. - 320 c. : ил.
|
|
|
|
Глава 3. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
3.1. ПОНЯТИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Пусть заданы два непустых множества D и E. Если каждой паре значений (x, y) из данной области D соответствует определенное единственное значение то переменная z называется функцией двух переменных, а x и y называются независимыми переменными, или аргументами. Область D называется областью определения функции, множество
то переменная z называется функцией двух переменных, а x и y называются независимыми переменными, или аргументами. Область D называется областью определения функции, множество
 - множеством значений функции. Обозначение функции двух переменных: z = f (x, y), или z = F (x, y), или z = z (x, y).
- множеством значений функции. Обозначение функции двух переменных: z = f (x, y), или z = F (x, y), или z = z (x, y).
Частным значением функции z = f (x, y) называют число, соответствующее какой-либо определенной паре значений аргументов.
Для обозначения частного значения функции z = f (x, y) при x = x0 и
y=y0 употребляется символ или, что то же самое,.
или, что то же самое,.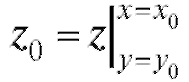 Каж-
Каж-
дая пара значений аргументов (x, y) геометрически определяет точку Р на плоскости xOy, а значение функции в этой точке есть аппликата z пространственной точки М (x, y, z). Геометрическое место всех точек М есть поверхность, взаимно однозначно проецирующаяся в область D на плоскости xOy (рис. 3.1). Эта поверхность служит геометрическим изображением (графиком) функции f (x, y).
Определение. Переменная величина U называется функцией независимых переменных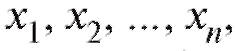 если каждой системе значений (x1,
если каждой системе значений (x1,  этих переменных из данной области их изменения соответствует единственное значение величины U. Обозначение:
этих переменных из данной области их изменения соответствует единственное значение величины U. Обозначение:
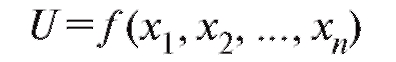
или
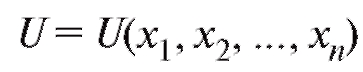 и т. д.
и т. д.
В случае функции трех переменных пишут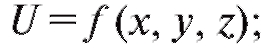 каж-
каж-
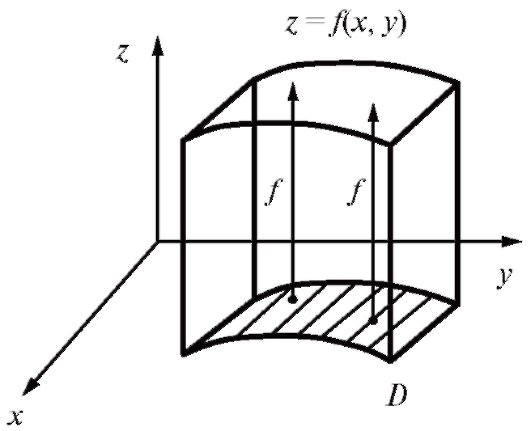
Рис. 3.1. Изображение функции двух переменных в трехмерном пространстве
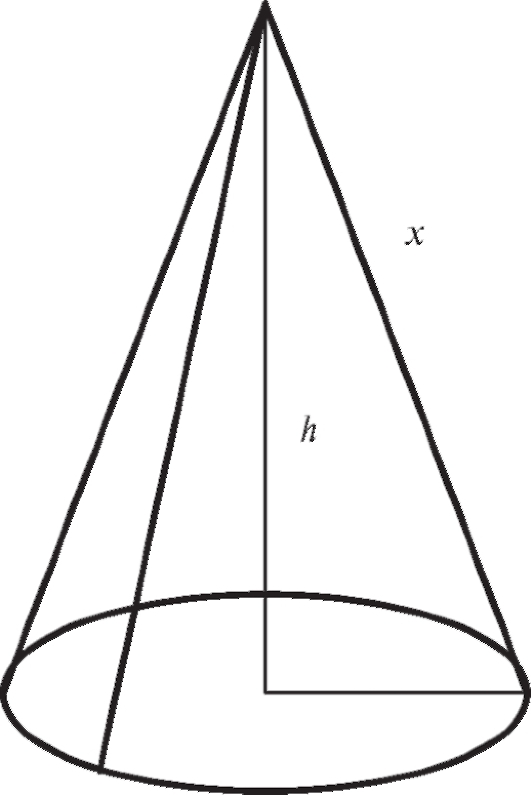
Рис. 3.2. Круговой конус
дая система (x, y, z) значений аргументов определяет некоторую точку М трехмерного пространства.
Пример 1. Выразить объем кругового конуса V как функцию его образующей x и радиуса основания y.
Решение. Объем кругового конуса (рис. 3.2) равен одной трети
произведения площади основания
S на высоту h. Так как S = πy2,
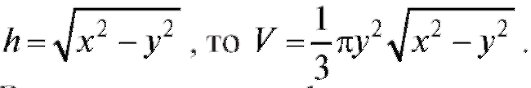
Это и есть искомая функция.
Пример 2. Найти частное значение функциив
точке Р (2; -1).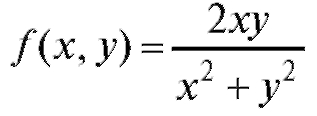 Решение.
Решение.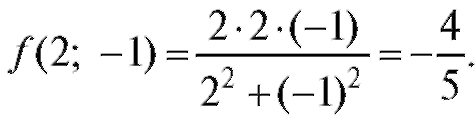
3.2. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ
Если функция задана аналитическим выражением (формулой) без каких-либо дополнительных условий, то под ее областью определения понимают совокупность всех точек, в которых данное аналитическое выражение определено и принимает только действительные значения.
Определение. Область D называется замкнутой, если она включает в себя все свои границы.
Область определения функции трех переменных представляет собой некоторую пространственную область, в частности некоторый объем.
Пример 1. Указать область определения функции, выражающей объем кругового конуса V через образующую х и радиус основания у.
Решение. Функция, найденная в примере 1 предыдущего пункта, выглядит так: 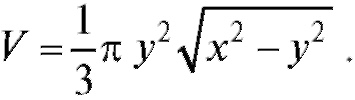 По смыслу задачи переменные х и у могут принимать только положительные значения, и при этом всегда х > у, так как гипотенуза больше катета (см. рис. 3.2). Следовательно, область
По смыслу задачи переменные х и у могут принимать только положительные значения, и при этом всегда х > у, так как гипотенуза больше катета (см. рис. 3.2). Следовательно, область
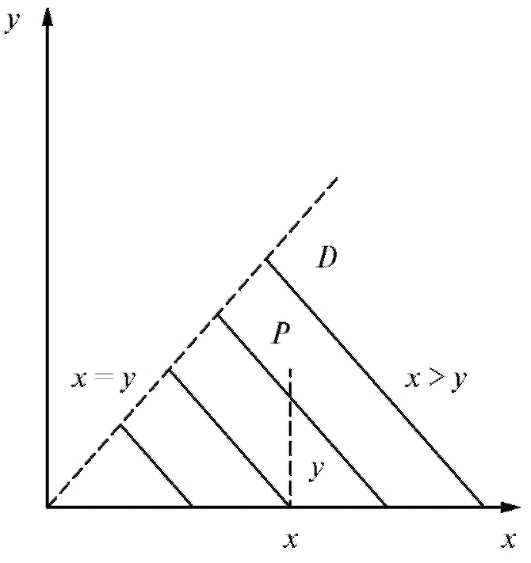
Рис. 3.3. К задаче о нахождении области определения
определения D задается неравенствами х > 0, у > 0, х > у, т. е. состоит из всех тех точек Р (х, у) первой четверти на плоскости хОу, которые лежат ниже биссектрисы х = у (рис. 3.3). Границами области D служат прямые у = 0, у = х, которые сами в область D не входят, так что эта область незамкнутая.
Пример 2. Найти область определения функции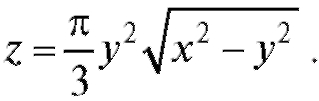
Решение. Поскольку никаких дополнительных ограничений на аргументы х и у не наложено, область определения D будет состоять из всех тех точек плоскости, для которых данное аналитическое выражение принимает действительные значения. Для этого подкоренное выражение должно быть неотрицательным, т. е. х2 - у2 > 0 или х2 > у2.
Если оставить здесь только знак равенства, то получится уравнение границы области D: x2 = y2 или x = + y. Эта граница состоит из двух биссектрис х = у и х = -у координатных углов. Для внутренних точек области D должно соблюдаться неравенство х > у или | x | > | y |. Следовательно, эти точки расположены между биссектрисами ближе к оси Ох, так как | y | есть расстояние точки Р (х ; у) до оси Ох и оно меньше расстояния | x | точки Р до оси Оу. Таким образом, область D состоит из всех точек двух углов между биссектрисами х = ± у, заключающими внутри себя ось Ох (рис. 3.4). Область замкнутая, так как включает в себя обе свои границы.
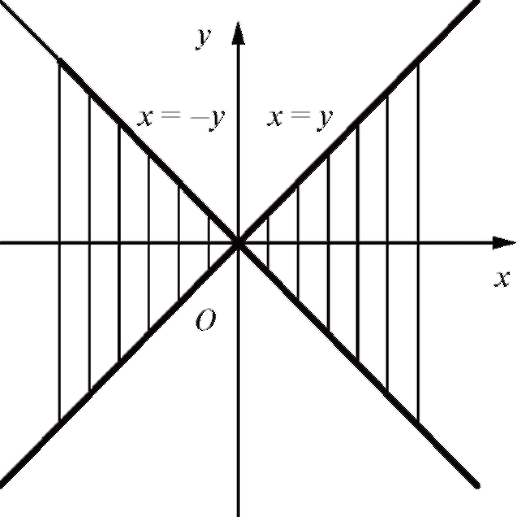
Рис. 3.4. Область определения функции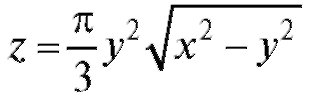
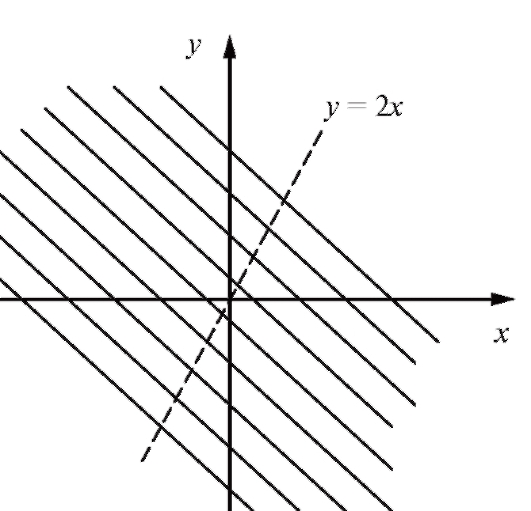
Рис. 3.5. Область определения функции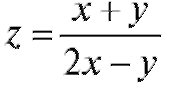
Замечание. Хотя аналитические выражения функции в примерах 1 и 2 одинаковые, их области определения разные. На переменные х и у в примере 1 были наложены дополнительные условия х > 0, у > 0, х > у, вытекающие из их геометрического смысла.
Пример 3. Найти область определения функции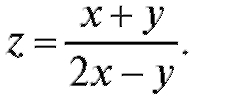
Решение. Выражение, стоящее справа, теряет смысл при тех значениях х и у, при которых знаменатель обращается в ноль. Отсюда областью определения нашей функции является вся плоскость, из которой выброшена прямая у = 2х (рис. 3.5).
Пример 4. Найти область определения функции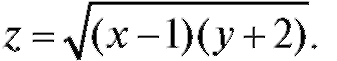
Решение. Для того чтобы квадратный корень имел вещественные значения, его подкоренное выражение должно быть неотрицательным. Решая неравенство (х - 1)(у + 2) > 0, находим, что либо
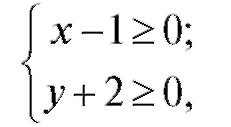
либо 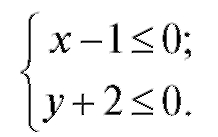
Решением 1-й системы неравенств является x > 1, y > -2. Чтобы получить изображение искомой области на координатной плоскости, достаточно провести две прямые х = 1 и у = -2. Область состоит из 2-х квадрантов с общей вершиной в точке (1; -2) (рис. 3.6).
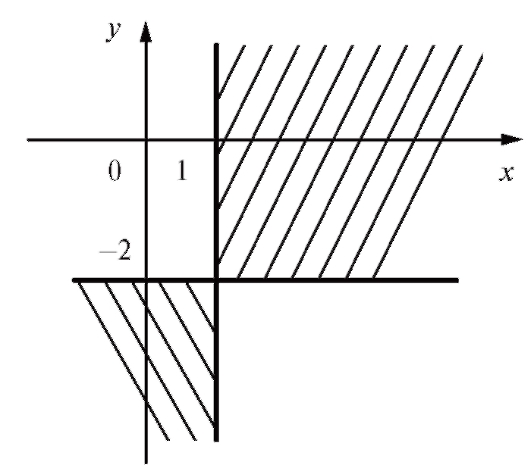
Рис. 3.6. Область определения функции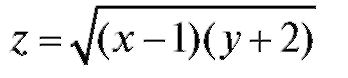
Пример 5. Найти область определения функции z = ln(9 + 9x - y2).
Решение. Логарифм определен только при положительном значении его аргумента, поэтому 9 + 9х - у2 > 0 или 9 + 9х > у2. Чтобы изобразить геометрически область D, найдем сначала ее границу 9 + 9х = у2 или у2 = 9 • (х + 1). Полученное уравнение определяет параболу, вершина которой расположена в точке О (-1; 0), а ось направлена в положительную сторону оси Ох. Точки пересечения параболы с осью Оу получаются из условия х = 0, откуда у2 = 9, т. е. у = ±3 (рис. 3.7). Парабола делит всю плоскость на две части - внутреннюю и внешнюю по отношению к параболе. Для точек одной из этих частей выполняется неравенство у2 < 9 • (х + 1), а для другой у2 > 9 • (х + 1) (на самой параболе у2 = 9 • (х + 1)). Чтобы установить, какая из этих 2-х частей является областью определения данной функции, т. е. удовлетворяет условию у2 < 9 • (х + 1), достаточно проверить это условие для какой-нибудь одной точки, не лежащей на параболе. Например, начало координат (0; 0) лежит внутри параболы и удовлетворяет нужному условию 0 < 9 • (0 + 1). Следовательно, рассматриваемая область D состоит из внутренних точек параболы. Сама парабола в область D входить не может, поскольку для точек параболы 9 + 9х - у2 = 0, и логарифм не определен.
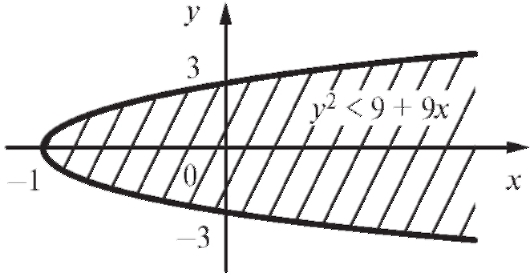
Рис. 3.7. Область определения функции z = ln(9 + 9x - y2)
Самостоятельная работа
1. Выразить площадь треугольника с данным периметром 2р как функцию длин двух его сторон x и y.
2. Выразить объем правильной шестиугольной пирамиды как функцию ее высоты х и бокового ребра y.
3. Найти f(0,5; 1) и f(2; -1), если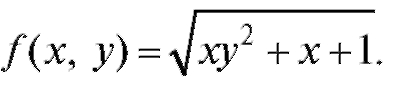
Найти области определения функций (4-22).
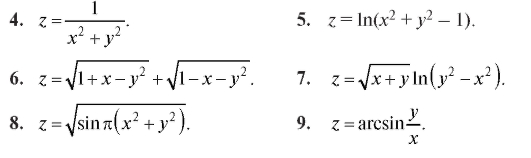

23. Указать область определения функции, выражающей площадь треугольника с данным периметром через длины двух его сторон.
3.3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ПОЛНЫЙ ДИФФЕРЕНЦИАЛ 3.3.1. Частные производные
Пусть (x, y) - произвольная фиксированная точка из области определения z = f (x, y). Рассмотрим предел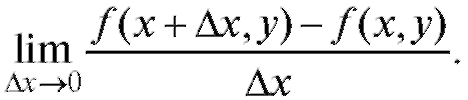 Этот
Этот
предел (если он существует) называется частной производной (первого порядка) данной функции z по переменной х в точке (х, у). Производная
обозначается одним из символов:
Аналогично,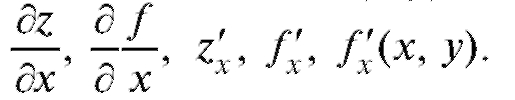
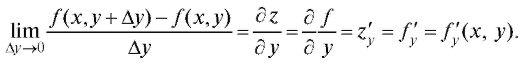
Частные производные функции z = f (x, y) сами представляют собой некоторые функции переменных х и у. Поэтому, если нас интересуют значения частных производных в какой-либо точке Р (х, у), надо снача-
ла по общим правилам найти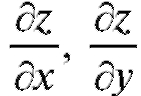 , а затем подставить в полученные
, а затем подставить в полученные
функции координаты точки Значения частных производных в точке Р0 обозначаются одним из символов:
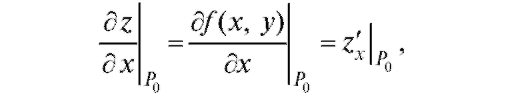
или
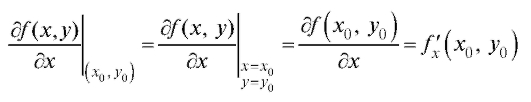
и аналогично - для производных по у.
Таким образом, частная производная функции z = f (x, y) по аргументу х есть производная этой функции по х при постоянном значении у.
Аналогично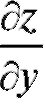 есть производная функции z = f (x, y) по у в предположении, что х является константой.
есть производная функции z = f (x, y) по у в предположении, что х является константой.
Частные производные функции нескольких переменных определяются как производные этой функции по одному из них при условии, что остальные переменные считаются постоянными. Например, производная функции u = f (x, y, z) по х определяется формулой
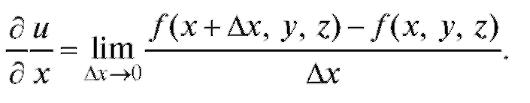
Пример 1. Найти частные производные функции z = x3 + y3 - 3axy. Вычислить их значения в точке Р0 (1; 1).
Решение. Считая у постоянным, находим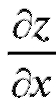 :
:
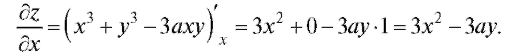
При нахождении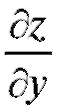 фиксируется аргумент х, т. е.
фиксируется аргумент х, т. е. 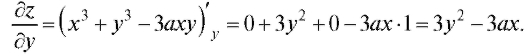 Значения производных в точке Р0 (1;1) следующие:
Значения производных в точке Р0 (1;1) следующие:
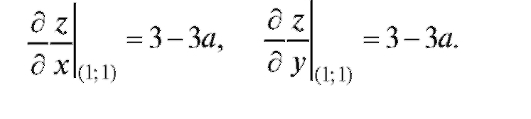
Пример 2. Найти частные производные функции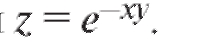 Решение. Находим частные производные, используя формулу дифференцирования сложной функции
Решение. Находим частные производные, используя формулу дифференцирования сложной функции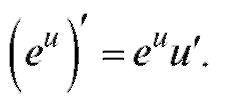
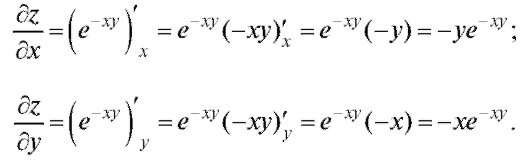
Пример 3. Доказать, что функция z = ln(x2 + xy + y2) удовлетворяет
уравнению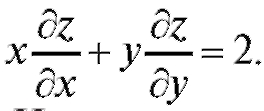
Решение. Находим частные производные:
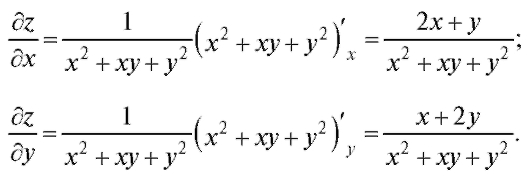
Подставляя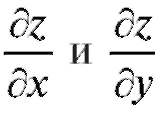 в данное уравнение:
в данное уравнение:
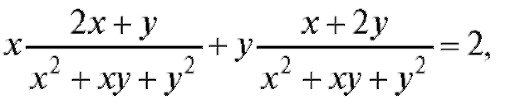
получим тождество.
3.3.2. Полный дифференциал
Пусть Р (х, у) - данная точка, а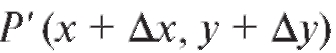 - близкая точка,
- близкая точка,
отвечающая приращениям аргументов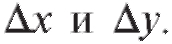 Полным приращением
Полным приращением
функции z = f (x, y) в точке Р называется разность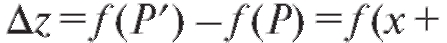
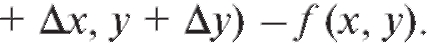 Если приращение
Если приращение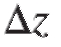 можно представить в виде
можно представить в виде  - бесконечно малая более высокого порядка по
- бесконечно малая более высокого порядка по
сравнению с расстоянием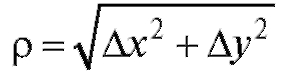 между точками Р и Р' (т. е.
между точками Р и Р' (т. е.
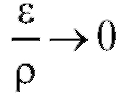 при
при ), то функция z = f (x, y) называется дифференцируемой в
), то функция z = f (x, y) называется дифференцируемой в
точке Р, а главная линейная часть ее приращения назы-
назы-
вается полным дифференциалом функции в точке Р. Функция, имеющая дифференциал в каждой точке некоторой области D, называется дифференцируемой в этой области.
Если функция дифференцируема, то необходимо, чтобы выполнялось:
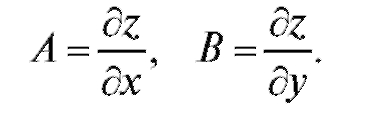
Достаточным условием дифференцируемости является наличие непрерывных частных производных. Так как приращения независимых переменных совпадают с их дифференциалами, т. е.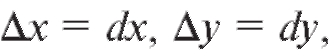 то полный дифференциал функции z = f (x, y) вычисляется по формуле:
то полный дифференциал функции z = f (x, y) вычисляется по формуле:
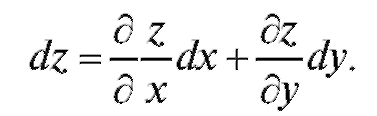 (3.1)
(3.1)
Последняя формула остается справедливой также и в том случае, когда х и у в свою очередь являются функциями каких-либо других аргументов (свойство инвариантности полного дифференциала).
Пример. Найти полный дифференциал функции z = x2y - y2x.
Решение. Находим частные производные:
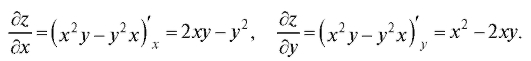
По формуле (3.1) имеем:
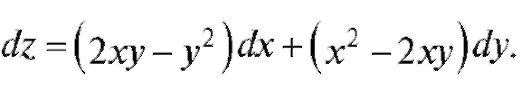
3.3.3. Применение дифференциала к приближенным вычислениям
Приращение функции и ее полный дифференциал
и ее полный дифференциал связаны равенством
связаны равенством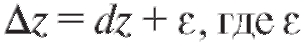 - бесконечно малая величина более высокого
- бесконечно малая величина более высокого
порядка малости по сравнению с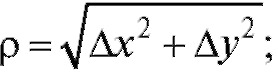 при достаточно малых
при достаточно малых
приращениях аргументов можно величиной 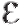 пренебречь и считать
пренебречь и считать
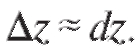 Это приводит к приближенному равенству
Это приводит к приближенному равенству
или (подробно):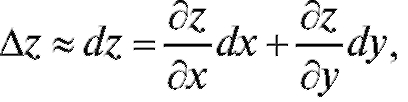
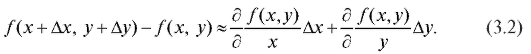
Этой формулой можно пользоваться для приближенного вычисления значения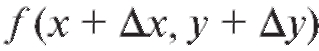 по известным значениям функции z = f (x, y)
по известным значениям функции z = f (x, y)
и ее частных производных в данной точке Р (х, у). Пример 1. Вычислить приближенно число (1,04)2,03. Решение. Рассмотрим функциюf (x, y) = xy. Данное число есть приращенное значение этой функции в точке Р0 (1; 2) при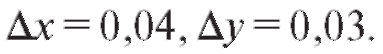 Дифференциал данной функции:
Дифференциал данной функции:
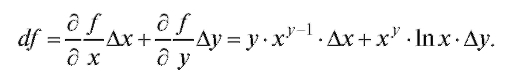
Его значение в точке Р0 (1; 2) при данных приращениях: 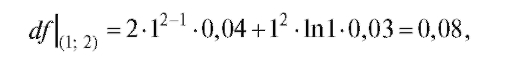 поэтому по формуле (3.2) имеем
поэтому по формуле (3.2) имеем 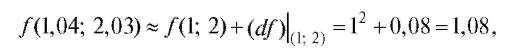 т. е.
т. е.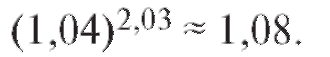
Пример 2. Вычислить приближенно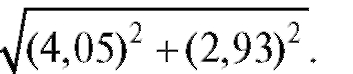
Решение. Рассмотрим функцию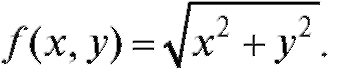 Данное число есть
Данное число есть
приращенное значение этой функции в точке Р0 (4; 3) при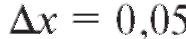 ,
,
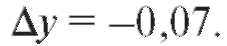 Полный дифференциал данной функции:
Полный дифференциал данной функции:
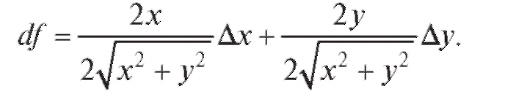
Его значение в точке Р0 (4; 3) при данных приращениях 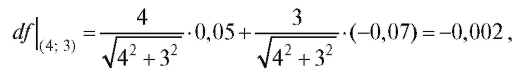 поэтому по формуле (3.2) с учетом равенства
поэтому по формуле (3.2) с учетом равенства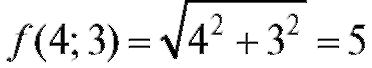 имеем
имеем
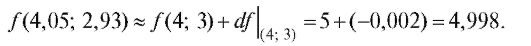
Итак,
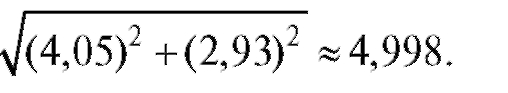
Пример 3. Вычислить приближенно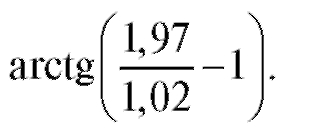
Решение. Данное число есть приращенное значение этой функции в точке Р0 (2; 1) при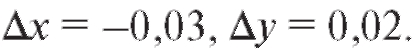 Найдем частные производные
Найдем частные производные
функции f (x, y) их значения в точке Р0 (2; 1):
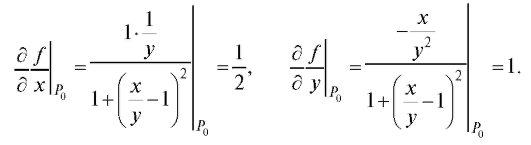
Значение функции в точке Р0 (2; 1) равно
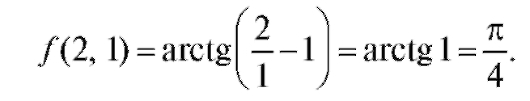
Подставляя найденные значения функции и частных производных в формулу (3.2), получим
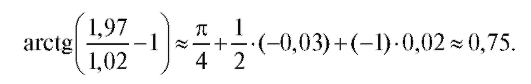
Самостоятельная работа
Найти частные производные функций (1-15).
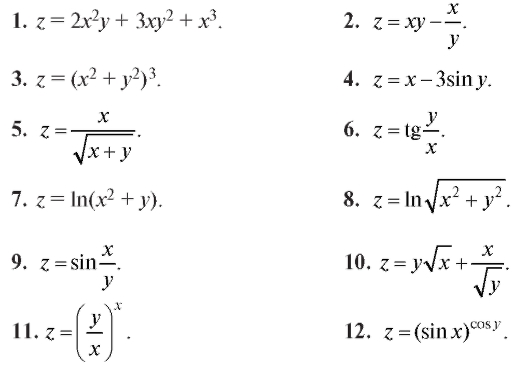

3.4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
Частными производными второго порядка функции z = f (x, y) называются частные производные от ее первых производных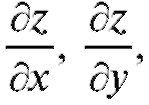 т. е.
т. е.
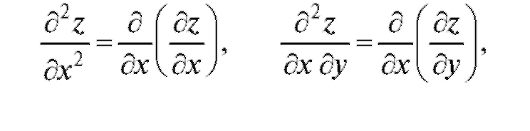
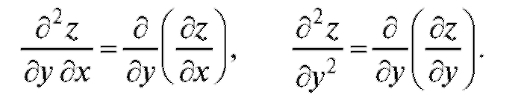
Частные производные второго порядка обозначаются также символами: 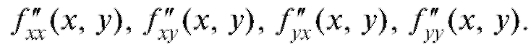 Частные производные
Частные производные
второго порядка вида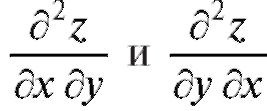 называются смешанными производ-
называются смешанными производ-
ными. Они не зависят от порядка дифференцирования, т. е. равны между собой, если выполняется условие следующей теоремы.
Теорема 3.1. Если функция z = f (x, y) определена в некоторой области D и ее частные производные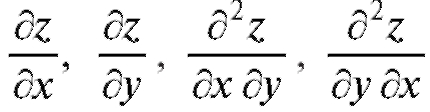 определены и непрерывны в этой области D, то значения смешанной производной не
определены и непрерывны в этой области D, то значения смешанной производной не
зависят от порядка дифференцирования, т. е.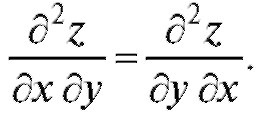
Аналогично определяются и обозначаются частные производные более высоких порядков.
Дифференциалы второго, третьего и более высоких порядков от функции z = f (x, y) определяются формулами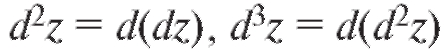 и
и
выражаются через частные производные следующим образом:
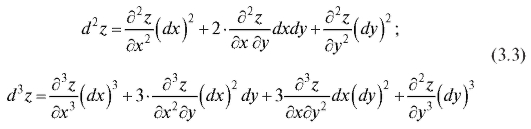
и т. д.
При этом приращении dx и dy рассматриваются как постоянные и остаются одними и теми же при переходе от дифференциала первого порядка к дифференциалу более высокого порядка.
Пример 1. Найти частные производные второго порядка функции
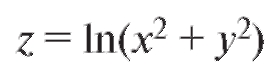 . Убедиться, что
. Убедиться, что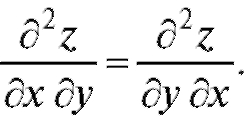
Решение. Находим сначала частные производные первого порядка:
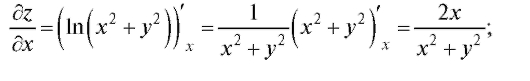
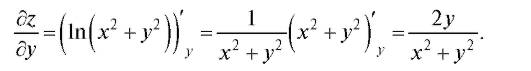
Дифференцируя каждую из полученных функций по х и у, найдем частные производные второго порядка:
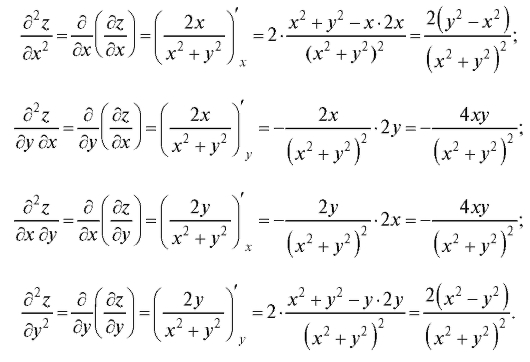
Отсюда видно, что смешанные частные производные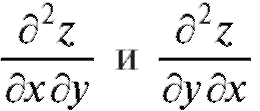
равны. Интересно отметить, что для данной функции производные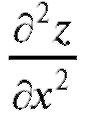
и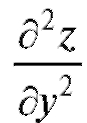 отличаются только знаком, т. е.
отличаются только знаком, т. е.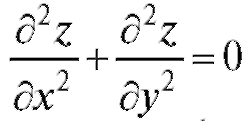 . Это уравнение на-
. Это уравнение на-
зывается уравнением Лапласа. Мы показали, что функция z = ln(x2 + y2) есть одно из решений уравнения Лапласа.
Пример 2. Найти дифференциал второго порядка функции z = 3x2y - 2xy + y2 - 1.
Решение. Находим частные производные первого и второго порядков:
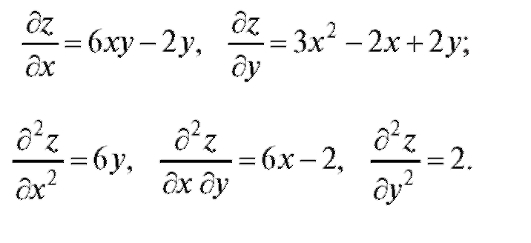
Следовательно, по формуле (3.3)
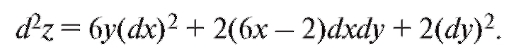
Тот же результат можно получить и другим способом. Найдем сначала первый дифференциал данной функции:
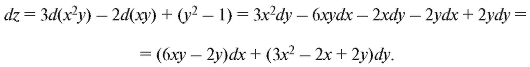
Беря дифференциал от dz, найдем d2z, при этом dx и dy надо считать постоянным:
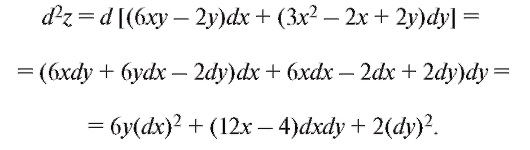
Самостоятельная работа
Найти вторые частные производные функций (1-9).