ЛЕКЦИЯ 27 ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ КВАНТОВОЙ МЕХАНИКИ.

Во времена Ньютона большинство физиков рассматривали свет как поток особых частиц. Правда, полного согласия по этому вопросу не было. Так, современник Ньютона Гюйгенс считал свет волнами, распространяющимися в особой среде - эфире. Спор о природе света заканчивается в 19 веке, когда были поставлены опыты, демонстрирующие дифракцию света. После этого волновая природа света становится общепризнанной. Работы Максвелла позволяют выяснить природу световых волн: свет - электромагнитные волны. При этом среди всех известных видов электромагнитного излучения свету отводится достаточно скромное место между инфракрасным и ультрафиолетовым излучениями. Электромагнитная теория света торжествует. Остается одно досадное недоразумение - никак не удается объяснить наблюдаемые закономерности теплового излучения.

В самом начале 20 века Макс Планк строит теорию теплового излучения исходя из предположения о дискретном характере испускания тепловых волн: тепловое излучение испускается отдельными порциями с энергией Е = hv (h - постоянная Планка). Немного позже Эйнштейн объясняет явление фотоэффекта исходя из предположений о дискретном характере процесса поглощения: свет поглощается отдельными порциями с энергией Е = hv.

Таким образом, выясняется, что свет имеет двойственную природу. При распространении он ведет себя как волна, а при взаимодействии с веществом как поток особых частиц - фотонов. Сочетание волновых и корпускулярных свойств получило название корпускулярно-волнового дуализма.

27.2. Волновые свойства частиц. Дифракция электронов

Французский физик Луи де Бройль высказал предположение о том, что корпускулярно-волновой дуализм присущ не только свету, но и любым частицам. При этом он исходил из следующих соображений.

• Свет с длиной волны λ обладает корпускулярными свойствами: состоит из фотонов с энергией Е = hv и импульсом р = h/λ (эта формула получена Эйнштейном).

• Частица с импульсом р = mv обладает волновыми свойствами. При этом связь между длиной волны и импульсом частицы такая же, как у фотона: р = h/λ → λ = h/р = h/(mv).

Если гипотеза де Бройля справедлива, то поток частиц массы m, движущихся со скоростью v, должен обладать свойствами волны с длиной

λ = h/(mv). (27.1)

Наличие волновых свойств у частиц было подтверждено экспериментально: в 1927 г. были поставлены опыты, в которых наблюдалась дифракция электронов на кристаллах. Волны, соответствующие движению частиц, были названы волнами де Бройля.

27.3. Электронный микроскоп

Обнаружение волновых свойств частиц инициировало разработку и создание электронного микроскопа, в котором вместо света используется поток электронов, ускоренных электрическим полем. Электронные волны можно фокусировать (с помощью электрических и магнитных полей) и получать с их помощью изображения предметов. Конструкция электронного микроскопа показана на рисунке 27.1.

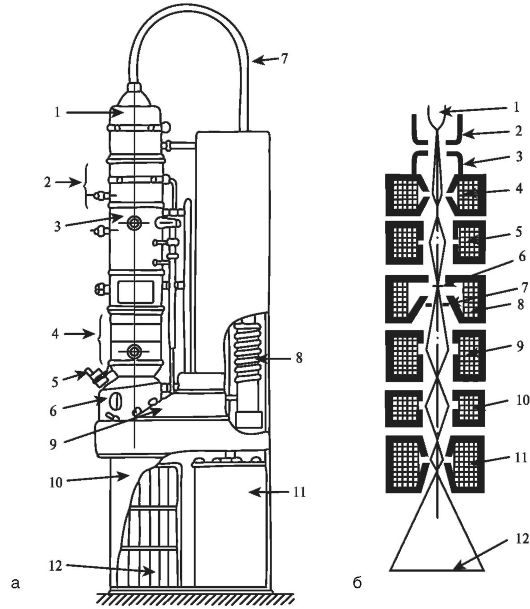Рис. 27.1. Электронный микроскоп просвечивающего типа: а - Конструкция: 1 - электронная пушка; 2 - конденсорные магнитные линзы; 3 - объектив; 4 - проекционные магнитные линзы; 5 - световой микроскоп, дополнительно увеличивающий изображение, наблюдаемое на экране: 6 - тубус со смотровыми окнами, через которые можно наблюдать изображение; 7 - высоковольтный кабель; 8 - вакуумная система; 9 - пульт управления; 10 - стенд; 11 - высоковольтное питающее устройство; 12 - источник питания линз;

б - Оптическая схема ПЭМ: 1 - катод (источник электронов); 2 - фокусирующий цилиндр; 3 - анод; 4,5 - конденсоры, направляющие электроны на объект; 6 - объект; 7 - апертурная диафрагма; 8 - объектив; 9, 10, 11 - система проекционных линз (окуляр); 12 - катодолюминесцентный экран, на котором формируется конечное изображение.

В лекции 25 мы выяснили, что разрешающая способность оптического микроскопа ограничена длиной волны видимого света (см. формулу 25.5). Длины волн де Бройля во много раз меньше. Электроны, прошедшие разность потенциалов U, приобретают скорость

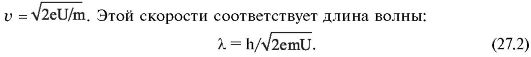Уже при величине ускоряющего напряжения до U = 10 кВ длина электронной волны λ ≈ 0,01 нм. Это в десятки тысяч раз меньше, чем длина световой волны. Во столько же раз меньше и предел разрешения электронного микроскопа. При ускоряющем напряжении U = 100 кВ и угловой апертуре порядка 10^-2 рад предел разрешения электронного микроскопа равен Z = 0,1 нм = 10^-10 м, что в 30 000 раз меньше предела разрешения оптического микроскопа. Увеличение, даваемое электронным микроскопом, достигает величины Г = 10⁶.

Конструкция и принципиальная оптическая схема электронного микроскопа просвечивающего типа представлены на рис. 27.1.

Элементы электронного микроскопа по своему назначению соответствуют оптическому. Их сопоставление приводится ниже.

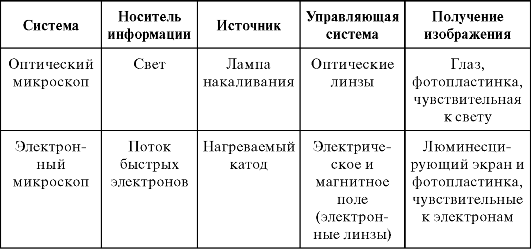Образцы для электронного микроскопа требуют специальной подготовки. Это связано с тем, что поток электронов сильно поглощается (что приводит к разогреванию) и рассеивается веществом, поэтому готовят тонкие срезы (порядка 0,1 мкм). Часто делают оттиск исследуемой поверхности объекта на тонком слое полимерного материала.

Такие тонкие копии поверхности предмета называются реплики. В электронном микроскопе в этом случае рассматривают не сам объект, а его реплику.

Использование электронного микроскопа позволило «увидеть» отдельные молекулы, в том числе и молекулы многих биологических систем.

27.4. Основные представления квантовой механики

Обнаружение корпускулярных свойств света и волновых свойств частиц послужило толчком к разработке новой физической теории, названной квантовой механикой. Оказалось, что детерминизм, присущий классической физике, в квантовой механике полностью отсутствует. Кантовая механика - вероятностная теория. При описании движения частицы квантовая механика использует не ее координаты, а вероятности обнаружить частицу в той или иной области. Это и выявляет дифракция электронов. В те места экрана, для которых эта вероятность значительна, в соответствии с законом больших чисел попадает много электронов. Там и образуются дифракционные максимумы.

Одним из фундаментальных положений квантовой механики является принципиальная невозможность одновременного точного определения некоторых пар характеристик квантовой системы. Это положение нашло свое математическое выражение в соотношениях неопределенностей, полученных В. Гейзенбергом (1927 г.). Мы рассмотрим только одну пару таких величин: энергия - время.

Соотношение неопределенностей для энергии и времени

Пусть известно, что квантовая система находится в некотором состоянии в течение временного интервала (t, t + Δt) и обладает в этом состоянии энергией из интервала (Е, Е + ΔЕ). Величины At и AE также называются неопределенностями. Соотношение между неопределенностями энергии и времени также записывается в виде неравенства:

Из соотношения (27.3) следует, что чем меньше интервал времени, в течение которого частица может находиться на некотором энергетическом уровне, тем более неопределенной является величина энергии, которой она обладает: если Δt → 0, то ΔE → ∞ да, и наоборот.

Дискретность энергетических состояний квантовой системы

Другим фундаментальным следствием квантовой механики является дискретность энергетических состояний, в которых может находиться квантовая система (система взаимодействующих микрочастиц). Дискретность энергетических состояний атома водорода была показана еще Бором. В квантовой механике это положение стало универсальным.

Для квантовой системы характерно наличие стационарных состояний, в которых она не испускает квантов электромагнитного излучения. Иные состояния невозможны. Энергии стационарных состояний образуют дискретный ряд значений Е₁, Е₂, Е₃..., которые называют энергетическими уровнями.

Простая схема энергетических уровней квантовой системы показана на рис. 27.2, а. Величины энергетических уровней отложены по вертикали, а сами уровни изображены горизонтальными отрезками.

Состояние с наименьшей энергией Е₁ называется основным. Другие стационарные состояния называются возбужденными. Возбужденные состояния неустойчивы. Поэтому спустя некоторое

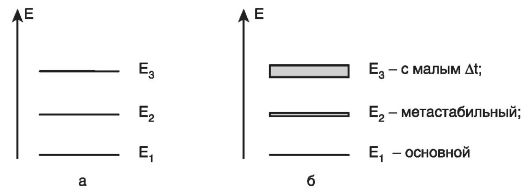Рис. 27.2. Схема энергетических уровней квантовой системы: а - простая; б - с учетом уширения

время At возбужденная система спонтанно возвращается в основное состояние Е₁. Например, Е₃ → Е₁ или Е₃ → Е₂ → Е₁.

Принцип неопределенности вносит в картину энергетических уровней некоторую поправку. Время нахождения атома в возбужденном состоянии - случайная величина, а At - ее среднее значение. Неопределенность во времени приводит к неопределенности в энергии

(27.3):

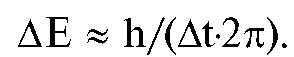Поэтому энергетические уровни стационарных состояний «размазаны» и их следует изображать в виде полос. Чем меньше время жизни для данного состояния, тем шире его полоса. В основном состоянии (Е₁) Δt = ∞, а ΔE = 0. Для состояний с малым временем жизни уширение энергетических уровней весьма заметно. Для состояний с большим временем жизни - их называют метастабильными - уширение мало, и им можно пренебречь. На рисунке 27.2, б показаны энергетические уровни с учетом их уширения.

Переход с верхнего уровня (k) на нижний (i) может сопровождаться испусканием электромагнитного кванта с частотой v_ki, определяемой равенством

Такой переход называется излучательным (рис. 27.3). Чем уже верхний уровень, тем больше время его релаксации (жизни) и тем больше вероятность излучательного перехода. Собственно говоря, уровень является долгоживущим именно потому, что безызлучательный переход для него маловероятен.

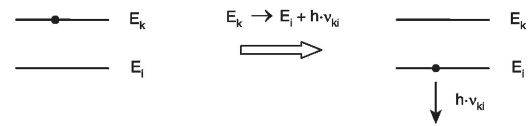Рис. 27.3. Схема спонтанного излучательного перехода

Однако спонтанный переход может и не сопровождаться излучением. В этом случае энергия E_k - E_i передается соседним частицам. Такой переход называют безызлучательным. Именно безызлучательные переходы приводят к поглощению света в веществе.

Каким образом атом или молекула могут оказаться в возбужденном состоянии? Существуют две возможности.

• При столкновении двух частиц, находящихся в основном состоянии, часть кинетической энергии расходуется на возбуждение.

• Частица, находящаяся в основном состоянии E₁, взаимодействует с электромагнитным квантом, частота которого удовлетворяет равенству hv_k1 = E_k - E₁. При этом квант исчезает (поглощается), а частица переходит в возбужденное состояние E_k. Такое возбуждение называется фотонным (рис. 27.4).

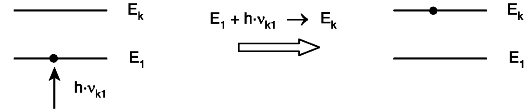Рис. 27.4. Схема фотонного возбуждения

Поглощение кванта может иметь место и в том случае, когда частица уже находится в возбужденном состоянии E_i. Для этого частота кванта должна удовлетворять уравнению (27.4):

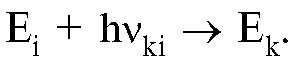Каким образом атом или молекула могут перейти из верхнего состояния в нижнее? Здесь существуют три возможности.

• Спонтанный излучательный переход.

• Безызлучательный переход при взаимодействии с соседними частицами.

• Вынужденный излучательный переход.

Схема вынужденного перехода изображена на рис. 27.5.

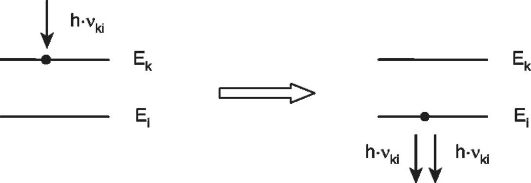Рис. 27.5. Схема возникновения вынужденного излучения

Если в частицу, находящуюся в возбужденном состоянии попадает квант света hv_ki, частота которого соответствует переходу с уровня k на какой-либо нижний уровнь i, то частица переходит на этот уровень, испуская аналогичный квант hv_ki. Исходный квант при этом сохраняется (он только «столкнул» частицу с верхнего уровня). Таким образом происходит удвоение квантов. Испущенный квант по частоте и фазе совпадает с квантом, вызвавшим переход.

На использовании вынужденного излучения основан принцип действия лазера.

Подведем некоторые итоги.

1. Дискретность энергетических состояний квантовой системы приводит к тому, что она может излучать и поглощать только те электромагнитные кванты, частоты которых удовлетворяют условию (27.4). Кванты других частот с системой не взаимодействуют.

2. Поглощение квантов еще не означает поглощения энергии электромагнитного излучения. Например, если поглощение кванта сопровождается двумя излучательными переходами, то энергия электромагнитного излучения не меняется, а лишь переходит в другую частотную область. Например:

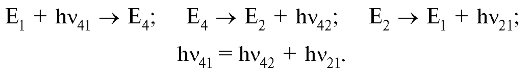Здесь после поглощения одного кванта (hv₄₁) излучаются два кванта (hv₄₂ и hv₂₁) с меньшими частотами.

3. Поглощение энергии электромагнитного излучения в веществе возможно лишь тогда, когда некоторые спонтанные переходы в основное состояние являются безызлучательными.

4. При вынужденном излучательном переходе происходит удвоение квантов. Испущенный квант по частоте и фазе совпадает с квантом, вызвавшим переход.

27.5. Основные понятия и формулы

окончание таблицы