ЛЕКЦИЯ 6 МЕХАНИЧЕСКИЕ СВОЙСТВА ТКАНЕЙ

При действии на тело внешней деформирующей силы расстояние между частицами меняется. Это приводит к возникновению внутренних сил, стремящихся вернуть атомы (ионы) в первоначальное положение. Мерой этих сил является механическое напряжение.

Растяжение (сжатие)

Этот вид деформации возникает, когда к стержню (бруску) с закрепленным основанием прикладывается сила F, направленная вдоль его оси (рис. 6.1, а). Под действием этой силы длина стержня увеличивается на некоторую величину Δl (l - первоначальная длина).

При этом в каждом сечении стержня возникают направленные по нормали силы (F₁ и F₂), равные по величине приложенной силе F и обусловленные изменением расстояния между частицами при растяжении. Сила F₁ действует на верхнюю часть бруска со стороны нижней части; сила F₂ - наоборот (рис. 6.1, б).

Состояние растянутого тела характеризуется продольным (нормальным) напряжением σ, которое может быть вычислено для любого сечения тела, перпендикулярного приложенной силе.

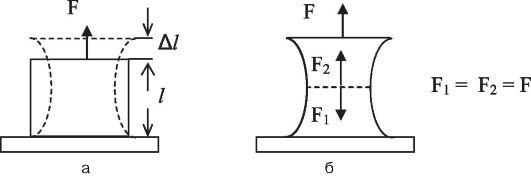Рис. 6.1. Деформация растяжения (а); силы, возникающие при растяжении (б)

Нормальное напряжение равно отношению модуля силы, возникающей в данном сечении в результате растяжения, к площади сечения:

В СИ механическое напряжение измеряется в паскалях (Па).

Величина абсолютной деформации А! зависит от первоначальной длины стержня, поэтому степень деформации выражают через отношение абсолютной деформации к первоначальной длине. Это отношение называется относительной деформацией (ε):

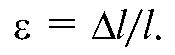Относительная деформация - величина безразмерная. Иногда ее выражают в процентах: ε = (Δl/l)х100%.

В большинстве случаев при растяжении или сжатии степень деформации в различных сечениях стержня различна. Это можно увидеть, если на поверхность тела нанести квадратную сетку. После деформирования сетка исказится. По характеру и величине этого искажения можно судить о распределении напряжения вдоль образца (рис. 6.2).

Видно, что изменения формы ячеек сетки максимальны в средней части стержня и почти отсутствуют на его краях.

Опытным путем было установлено, что небольшие деформации исчезают после снятия внешнего воздействия. Такие деформации называются упругими. Для них выполняется закон Гука:

При упругой деформации напряжение прямо пропорционально величине относительной деформации:

Коэффициент пропорциональности Е характеризует упругие свойства вещества при растяжении (сжатии) и называется модулем Юнга (модуль продольной упругости, Па). В таблице 6.1 представлены значения модулей упругости некоторых материалов.

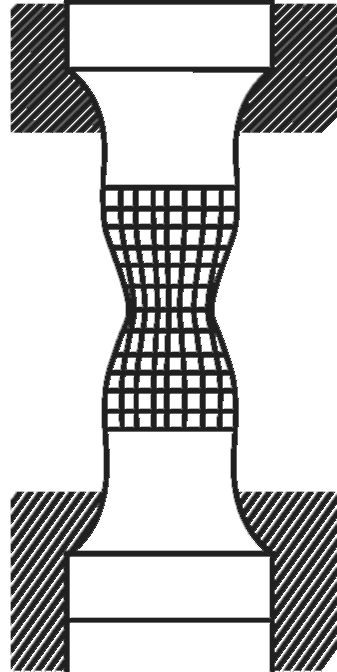Рис. 6.2. Искажение квадратной сетки при растяжении стержня

Сдвиг

Деформация сдвига возникает, если на тело действует касательная сила, приложенная параллельно закрепленному основанию (рис. 6.3, а).

В этом случае направление смещения свободного основания параллельно приложенной силе и перпендикулярно боковой грани. В результате деформации сдвига

прямоугольный параллелепипед превращается в косоугольный. При этом боковые грани смещаются на некоторый угол γ, называемый углом сдвига.

При сдвиге в каждом сечении стержня возникают касательные силы (F₁ и F₂), равные по величине приложенной силе F и обусловленные изменением расстояния между частицами (рис. 6.3, б). Сила F₁действует на верхнюю часть бруска со стороны нижней части; сила F₂ - наоборот.

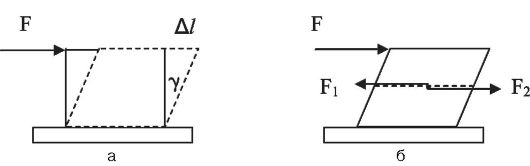Рис. 6.3. Деформация сдвига (а); силы, возникающие при сдвиге (б)

Состояние тела при наличии деформации сдвига характеризуется касательным напряжением τ, которое может быть вычислено для любого сечения тела, параллельного закрепленному концу.

Касательное напряжение равно отношению модуля силы, возникающей в данном сечении в результате сдвига, к площади сечения:

Абсолютная деформация сдвига измеряется величиной смещения свободного основания Δl. Относительная деформация сдвига определяется через тангенс угла сдвига tgγ, называемый относительным сдвигом. Так как угол γ обычно мал, то можно считать tg(γ) ≈ γ.

При небольшой величине относительной деформации сдвига связь между деформацией и механическим напряжением выражается законом Гука:

Коэффициент пропорциональности G характеризует упругие свойства вещества при сдвиге и называется модулем сдвига (Па).

Всестороннее сжатие

Если тело поместить в жидкую или газообразную среду, то на его поверхность будут действовать силы давления, перпендикулярные его поверхности. Эти силы вызовут сближение частиц тела, в результате чего произойдет уменьшение линейных размеров и объема тела. Такая деформация называется всесторонним или гидростатическим сжатием (рис. 6.4).

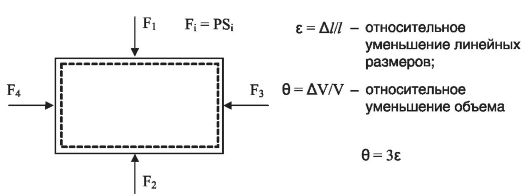Рис. 6.4. Всестороннее (гидростатическое) сжатие

Относительная деформация при всестороннем сжатии характеризуется либо относительным уменьшением объема:

где K - модуль всестороннего сжатия (модуль объемного сжатия, объемный модуль). Знак «минус» означает, что объем уменьшается с увеличением напряжения.

Сжимаемость - важнейшая характеристика вещества, которая позволяет судить о зависимости физических свойств от межатомных (межмолекулярных) расстояний.

Изгиб

Этот вид деформации характеризуется искривлением оси или срединной поверхности деформируемого объекта (балка, стержень) под действием внешних сил (рис. 6.5).

При изгибе один наружный слой стержня сжимается, а другой наружный слой растягивается. Средний слой (называемый нейтральным) изменяет лишь свою форму, сохраняя длину (рис. 6.5, а). Степень деформирования бруска, имеющего две точки опоры (рис. 6.5, б), определяется по перемещению λ, которое получает его середина.

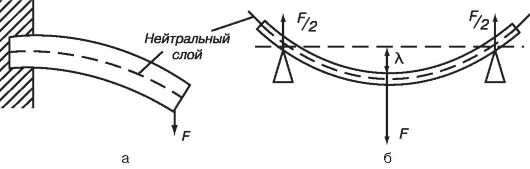Рис. 6.5. Деформация изгиба:

а - стержень закреплен на одном конце; б - стержень опирается на две опоры

Величина λ называется стрелой прогиба. В теории сопротивления материалов показано, что стрела прогиба находится по формуле:

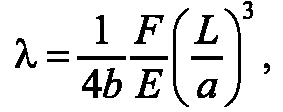где F - сила; b - ширина; L - длина; a - толщина; E - модуль упругости.

Материал, находящийся в нейтральном слое, не работает, а лишь утяжеляет конструкцию. Поэтому часть вещества около этого нейтрального слоя можно удалить без большого ущерба для прочности балки, работающей на изгиб. Так добиваются уменьшения массы конструкции при сохранении заданной прочности. Например, сплошные брусья заменяют трубами, балки делают тавровыми или двутавровыми. Трубчатое строение имеют кости конечностей, стебли быстрорастущих растений-злаков и т.п.

Применительно к прямому брусу в зависимости от направления действующих сил изгиб называют продольным или поперечным.

Рис. 6.6. Различные виды изгиба:

а - продольный, б - поперечный, в - продольно-поперечный

Продольный изгиб возникает под действием сил, направленных вдоль бруса и приложенных к его концам навстречу друг другу (рис. 6.6, а). Образец приобретает форму арки. Поперечный изгиб возникает под действием сил, направленных перпендикулярно брусу и приложенных как к его концам, так и в средней части (рис. 6.6, б). Встречается также и смешанный продольно-поперечный изгиб (рис. 6.6, в).

Кручение

Этот вид деформации характеризуется взаимным поворотом поперечных сечений стержня под влиянием моментов (пар сил), действующих в плоскости этих сечений. Кручение возникает, например, когда нижнее основание стержня закреплено, а верхнее основание поворачивают вокруг продольной оси (рис. 6.7).

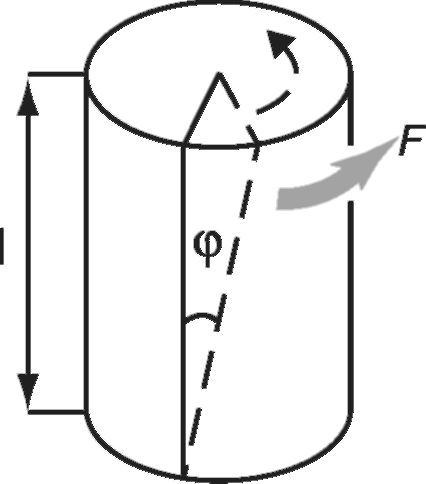Рис. 6.7. Деформация кручения

При этом расстояние между различными слоями остается практически неизменным, но точки слоев, лежащие на одной вертикали, сдвинуты относительно друг друга. Этот сдвиг в разных местах будет различен. Например, в центре сдвига совсем не будет, по краям он будет максимальный.

Таким образом, деформация кручения сводится к неоднородному сдвигу.

Абсолютная деформация при кручении характеризуется углом поворота (φ) одного основания относительно другого.

Относительная деформация (θ) равна отношению угла φ к длине стержня l:

Сопротивление кручению очень быстро возрастает с увеличением радиуса, поэтому органы, рассчитанные на выполнение крутильных движений, как правило, длинные и тонкие (шея птиц, тело змеи).

Сравнивания различные способы деформирования однородных тел, можно увидеть, что все они сводятся к комбинации растяжения (сжатия) и сдвига.

6.2. Механические свойства материалов и методы их исследования

До сих пор мы рассматривали относительно небольшие деформации, для которых выполняется закон Гука. Рассмотрим теперь особенности, которые появляются при значительных величинах относительной деформации.

Зависимость напряжения от величины деформации

На рисунке 6.8 показана зависимость относительной деформации при растяжении твердых тел от величины механического напряжения.

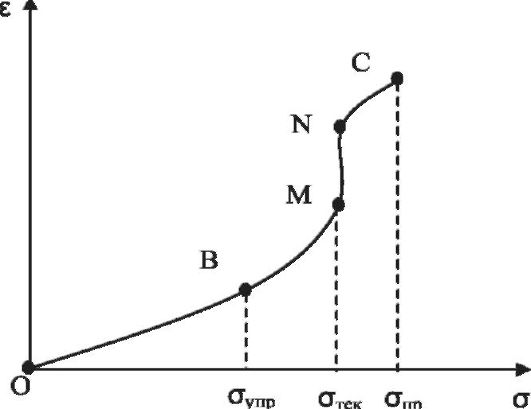Рис. 6.8. Зависимость деформации от напряжения - диаграмма растяжения

Наклонный прямолинейный участок ОВ соответствует упругой деформации, для которой справедлив закон Гука и которая исчезает после снятия нагрузки. Значения ε и σ для точки «В» являются предельными - выше этих значений деформация перестает быть упругой.

Участок BM соответствует пластической деформации, которая не исчезает после снятия нагрузки.

Вертикальный прямолинейный участок MN соответствует деформации текучести, которая возрастает без увеличения напряжения. Напряжение, начиная с которого деформация становится текучей, называется пределом текучести (σ _тек).

Участок NC - деформация перед разрушением. Точка С - предел прочности; σ_пр - механическое напряжение, при котором происходит разрушение образца. Предел прочности зависит от способа деформирования и свойств материала.

Ползучесть

Пластическая деформация, развивающаяся во времени, называется ползучестью.

Ползучесть - процесс изменения во времени размеров образца под действием постоянной нагрузки.

Ползучести подвержены все кристаллические и аморфные твердые тела при всех видах механических нагрузок. Ползучесть материалов проявляется при температурах, как близких к температуре жидкого

гелия, так и близких к их температуре плавления. Однако с увеличением температуры скорость ползучести растет, что ограничивает долговечность конструкций, работающих при постоянных нагрузках и повышенных температурах.

Исследование ползучести материалов осуществляется посредством метода, в котором к образцу (как правило, в форме стержня) подвешивается груз, под весом которого длина образца увеличивается. Процесс установления размеров образца может продолжаться очень долго. Механическое напряжение σ при этом считается постоянным. Изменение деформации со временем представлено на рис. 6.9.

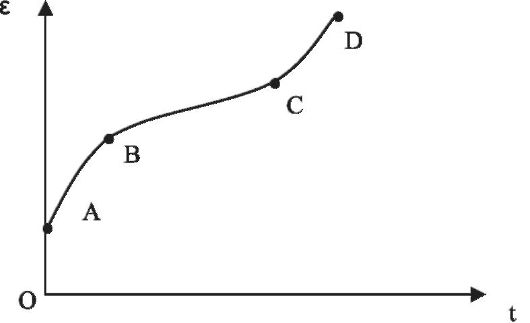Рис. 6.9. Кривая ползучести: σ = const; ε = f(t)

На кривой ползучести можно выделить несколько типичных участков: участок ОА - мгновенная упругая деформация; участок АВ - участок неустановившейся ползучести; ВС - участок установившейся ползучести, где скорость деформации постоянна; CD - участок ускоренной ползучести, где скорость ползучести возрастает; в точке D происходит разрушение.

Релаксация напряжения

С явлением ползучести тесно связано явление релаксации напряжения. Если образец растянуть до некоторой длины (т.е. создать деформацию) и закрепить его в этом положении с помощью динамометров, то с течением времени показания динамометров (пропорциональные механическому напряжению) будут уменьшаться. Происходит явление релаксации (уменьшения, расслабления) напряжения, связанное со взаимными перемещениями макромолекул.

Релаксация напряжения - процесс уменьшения механического напряжения в образце при постоянной относительной деформации.

Изменение напряжения в образце со временем показано на рис. 6.10.

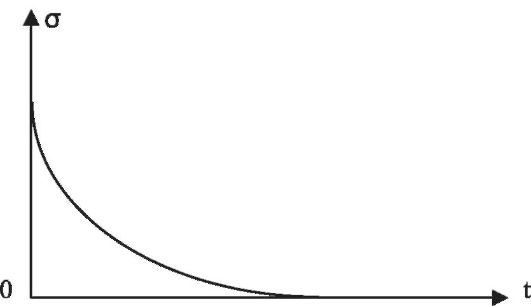Рис. 6.10. Релаксация напряжения: ε = const; σ = f(t)

Предел прочности и разрушение

Прочность - способность тел выдерживать без разрушения приложенную к ним нагрузку.

Прочность обычно характеризуют величиной предельного напряжения, вызывающего разрушение тела при данном способе деформирования.

Предел прочности - это максимальное напряжение, при котором образец еще не разрушается.

Предел прочности зависит как от строения вещества, так и от способа деформирования. Например, для бедренной кости человека предел прочности на сжатие равен 170 МПа, на растяжение - 124 МПа.

Определяют предел прочности путем постепенного увеличения механического напряжения вплоть до разрушения.

В табл. 6.2 представлены значения предела прочности некоторых тканей при сжатии.

Разрушение - макроскопическое нарушение сплошности тела (материала) в результате механических или каких-либо иных воздействий.

В процессе разрушения тела можно выделить две стадии: начальную - развитие пор, трещин, и конечную - разделение тела на две части и более.

В зависимости от того, как протекают эти стадии, различают пластическое (вязкое) и хрупкое разрушения.

Вязкое разрушение

При этом виде разрушения после завершения упругой и пластической деформаций начинаются необратимые изменения размеров и формы тела, обусловленные зарождением и развитием трещин в наиболее слабом месте. Скорость протекания процесса вязкого разрушения обычно невелика, а сам процесс можно замедлить (остановить), снизив приложенную нагрузку. Когда величина относительного растяжения достигает некоторого критического значения, происходит разрушение (разрыв) стержня.

Хрупкое разрушение

Это разрушение начинается практически сразу после завершения упругой деформации (прямолинейный участок) и характеризуется высокой скоростью протекания процесса. Зародившаяся трещина довольно быстро достигает критического размера, после чего происходит ее стремительное самопроизвольное распространение, завершающееся разрушением.

Основными факторами, определяющими характер процесса разрушения, являются:

• свойства материала и состояние вещества (структура вещества, температура, влажность и т.п.);

• свойства объекта (конструкционные особенности, размеры, форма, качество поверхности);

• динамика силового воздействия (скорость нагружения);

• направление механического воздействия.

Повреждения трубчатых костей

Хрупкое разрушение характерно, например, для длинных трубчатых костей. Разрушения таких костей можно рассматривать как разрушения стержня при воздействии нагрузок в продольном или поперечном направлениях.

Продольные нагрузки (сжатие) возникают, например, при падении на кисть вытянутой руки, на руку, согнутую в локтевом

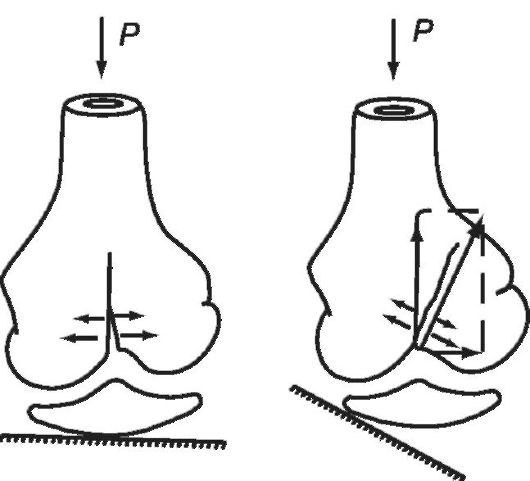Рис. 6.11. Повреждение нижнего эпифиза бедренной кости вследствие разрывных или сдвиговых деформаций возможно при падении на согнутое колено.

суставе, или на согнутое колено

(рис. 6.11).

В спортивной практике часто имеет место повреждение костей вследствие их изгиба под влиянием внешнего воздействия. Зона начала разрушения диафиза длинной трубчатой кости при изгибе располагается на выпуклой стороне (рис. 6.12) дуги, где сосредоточиваются наибольшие значения растягивающих напряжений.

Другой вид повреждений больших трубчатых костей, сопровождающийся множественными переломами, возникает при ударе тупым предметом (рис. 6.13).

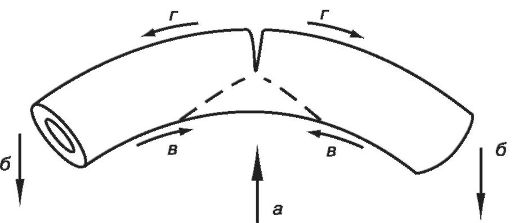Рис. 6.12. Схема разрушения диафиза длинной трубчатой кости вследствие изгиба:

а, б - векторы внешних усилий, в - сжимающие, г - растягивающие усилия

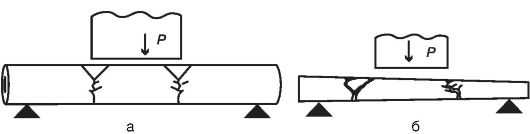Рис. 6.13. Схема механизма образования фрагментарного перелома диафиза длинной трубчатой кости с равномерным сечением (а) и с неравномерным сечением (б) при воздействии тупым предметом

6.3. Механические свойства биологических тканей

Структура материала является главным фактором, определяющим его механические свойства и характер процесса разрушения. Большинство биологических тканей являются анизотропными композиционными (от лат. - composition - сочетание) материалами, образованными объемным сочетанием химически разнородных компонентов. Состав каждого типа ткани сформировался в процессе эволюции и зависит от функций, которые она выполняет.

Костная ткань

Кость - основной материал опорно-двигательного аппарата. Так, в скелете человека более 200 костей. Скелет является опорой тела и способствует передвижению (отсюда и произошел термин «опорнодвигательный аппарат»). У взрослого человека скелет весит около 12 кг (18 % общего веса).

В компактной костной ткани половину объема составляет неорганический материал, минеральное вещество кости - гидроксилапатит. Это вещество представлено в форме микроскопических кристалликов. Другая часть объема состоит из органического материала, главным образом коллагена (высокомолекулярное соединение, волокнистый белок, обладающий высокой эластичностью). Способность кости к упругой деформации реализуется за счет минерального вещества, а ползучесть - за счет коллагена.

Кость является армированным композиционным материалом. Например, кости нижних конечностей армированы высокопрочными волокнами в окружных и спиральных перекрещивающихся направлениях.

Механические свойства костной ткани зависят от многих факторов: возраста, заболевания, индивидуальных условий роста. В норме плотность костной ткани 2400 кг/м³, а ее модуль Юнга Е = 10¹⁰ Па; предел прочности при растяжении σ_пр = 100 МПа, относительная деформация достигает 1%.

При различных способах деформирования (нагружения) кость ведет себя по-разному. Прочность на сжатие выше, чем на растяжение

или изгиб. Так, бедренная кость в продольном направлении выдерживает нагрузку 45 000 Н, а при изгибе - 2500 Н.

Запас механической прочности кости весьма значителен и заметно превышает нагрузки, с которыми она встречается в обычных жизненных условиях. (Живая кость в 5 раз прочнее железобетона.) Бедренная и берцовая кости выдерживают нагрузку в 25-30 раз больше веса нормального человека.

Особенность механического поведения костей состоит в том, что при их деформации проявляется пьезоэлектрический эффект. Если костную полоску, закрепленную на одном конце, изгибать, то в зоне деформации между противоположными сторонами регистрируется определенная разность потенциалов с отрицательным зарядом на вогнутой стороне (рис. 6.14).

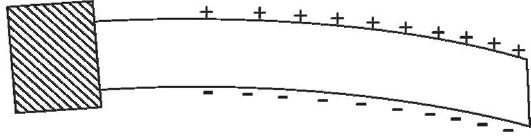Рис. 6.14. Проявление пьезоэффекта при деформации костной полоски

В интервале упругой деформации эта разность потенциалов пропорциональна механическому напряжению.

Кожа

Кожа представляет собой не только совершенный покров тела, но является сложным органом, выполняющим важные функции: поддержание гомеостаза; участие в процессе терморегуляции, регуляцию общего обмена веществ в организме, секреторную функцию (работу сальных и потовых желез), защиту от повреждающего действия механических, физических, химических, инфекционных агентов. Она представляет собой обширное рецепторное поле, воспринимающее извне и передающее в ЦНС целый ряд ощущений. Кожа - граница раздела между телом и окружающей средой, поэтому она обладает значительной механической прочностью.

Кожа - самый крупный орган тела. Она - важная анатомо-физиологическая часть целостного организма. Функции кожи зависят от состояния всего организма. При различных заболеваниях, в том числе и внутренних органов, в коже происходят те или иные изменения.

Кожу часто рассматривают как гетерогенную ткань, состоящую из трех наложенных друг на друга слоев, которые тесно связаны между собой, но четко различаются по природе, структуре, свойствам: эпидермиса, дермы, подкожной клетчатки. Эпидермис покрыт сверху роговым слоем.

Функции каждого слоя кожи, в том числе и механические, отражают биомеханическую природу компонентов и их структурную организацию.

В общий состав кожи входят волокна коллагена, эластина и основной ткани - матрицы. Коллаген составляет 75 % сухой массы, а эластин - около 4 %. Плотность кожи в норме (область руки, груди) составляет 1100 кг/м³. Эластин растягивается очень сильно (до 200- 300 %). Коллаген может растягиваться до 10 %. Механические характеристики компонентов кожи:

• коллаген - Е = 10-100 МПа, σ_пр = 100 МПа;

• эластин - Е = 0,5 МПа, σ_пр = 5 МПа.

Кожа является вязкоупругим материалом с высокоэластичными свойствами, она хорошо растягивается и удлиняется.

При исследовании механических свойств кожи с помощью акустического анализатора тканей, позволяющего оценивать скорость распространения акустических возмущений звукового диапазона (5-6 кГц), была выявлена акустическая анизотропия кожи, которая проявляется в том, что скорости распространения поверхностной волны во взаимно перпендикулярных направлениях - вдоль вертикальной (У) и горизонтальной (Х) осей тела - различаются. Для количественной оценки степени выраженности акустической анизотропии был использован коэффициент анизотропии К (см. формулу 2.10).

Проявление акустической анизотропии находится в соответствии с ориентацией линий естественного натяжения кожи, так называемых линий Лангера. Ориентация линий Лангера на коже лица и ладони представлена на рис. 6.15.

Ориентации линий Лангера на различных участках кожи и проявление акустической анизотропии показаны на рис. 6.16.

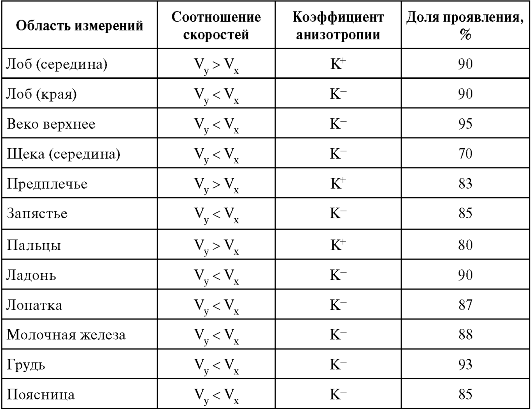
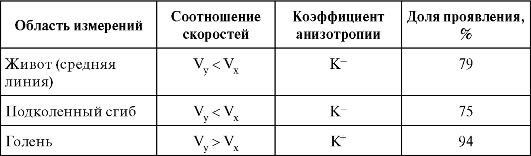
Проявление акустической анизотропии на различных участках кожи представлено в табл. 6.3, где указаны преимущественные соотношения скоростей и коэффициенты акустической анизотропии (данные указаны для лиц 18-30 лет). Доля проявления

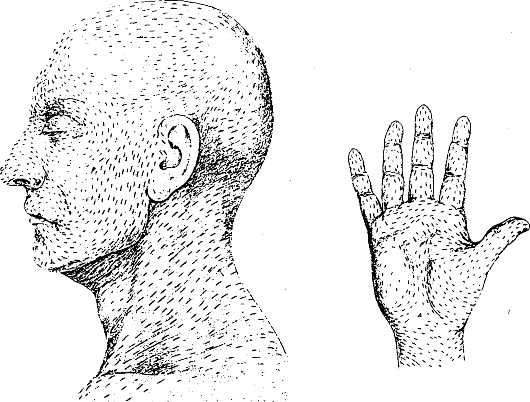Рис. 6.15. Ориентация линий Лангера на коже лица и ладони

соответствующей акустической анизотропии указана для лиц нормального телосложения.

Степень анизотропии кожи при некоторых патологиях сильно изменяется. Например, при псориазе, при атопических дерматитах (особенно в областях сгибательных поверхностей) или в коже верхнего века при прогрессирующей близорукости. Анизотропия кожи лица, особенно в области лба, позволяет оценивать возрастные изменения. Многочисленные исследования в самых различных областях медицины показали, что анизотропия кожи является объективным диагностическим критерием.

Мышечная ткань

Мышечная активность - это одно из общих свойств высокоорганизованных живых организмов. Вся жизнедеятельность человека связана с мышечной активностью. Она обеспечивает работу отде-

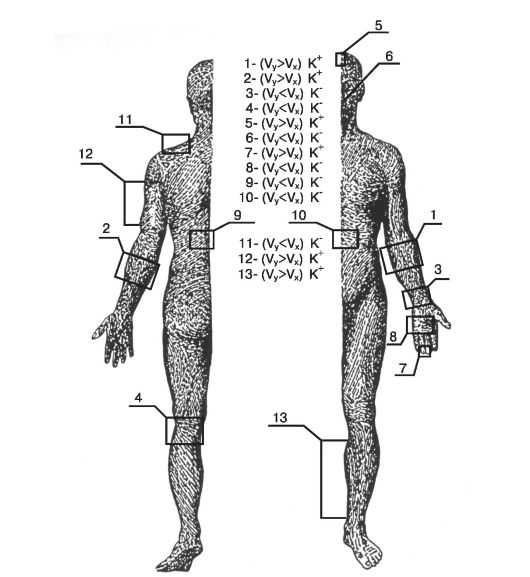Рис. 6.16. Проявление акустической анизотропии и ориентация линий Лангера на различных участках кожи

льных органов и целых систем: работу опорно-двигательного аппарата, легких, сосудистую активность, желудочно-кишечного тракта, сократительную способность сердца и т.д. Нарушение работы мышц может приводить к патологии, а ее прекращение - даже к летальному исходу (например, смерть при электротравме от удушья в результате парализации дыхательных мышц).

Мышцы разнообразны по форме, размерам, особенностям прикрепления, величине максимально развиваемого усилия. Количество мышц превышает число звеньев тела. Каждая мышца состоит из большого числа двигательных единиц, каждая из которых управляется через собственный мотонейрон. Таким образом, количество управляющих воздействий в мышечной (нервно-мышечной) системе огромно. Тем не менее эта система обладает удивительной надежностью и широкими компенсаторными возможностями, способностью не только многократно повторять одни и те же стандартные комплексы движений, но и выполнять нестандартные произвольные движения.

Деятельность мышц отражается в структурах движения. Благодаря этому отражению становится возможным, наблюдая движение, получать информацию о мышечной регуляции движения и ее нарушениях. Такой возможностью широко пользуются при диагностике заболеваний, при разработке специальных тестов для контроля двигательных навыков у спортсменов.

Независимо от назначения, особенностей строения и способов регуляции принцип работы различных мышц организма одинаков.

В состав мышц входит совокупность мышечных клеток (волокон), внеклеточное вещество (соединительная ткань), состоящее из коллагена и эластина. Поэтому механические свойства мышц подобны механическим свойствам полимеров. Мышцы по строению делятся на два вида: гладкие мышцы (кишечник, стенки сосудов, желудка, мочевого пузыря) и скелетные (мышцы сердца, мышцы, крепящиеся к костям и обеспечивающие движение головы, туловища, конечностей).

Среднее значение плотности мышечной ткани - 10-50 кг/м³, а модуль Юнга Е =10⁵ Па. Поведение гладких мышц во многих случаях описывается моделью Максвелла (рис. 6.19, в). Они могут значительно растягиваться без особого напряжения, что способствует увеличению объема полых органов, например мочевого пузыря. Мышцы способны деформироваться на десятки процентов, чему способствует распрямление молекул коллагена.

Механизм поведения скелетной мышцы соответствует модели Зинера (рис. 6.19, д) с соответствующими параметрами упругости и вязкости.

Для исследования характеристик сокращения мышц реализуют два искусственных режима.

Изометрический режим - когда напряжение мышцы происходит в искусственных условиях сохранения ее длины, что достигается с помощью фиксатора. Изотонический режим - когда искусственно поддерживается постоянство напряжения мышцы. Например, мышца поднимает постоянный груз Р = const, а регистрируется изменение ее длины при сокращении.

В процессе жизнедеятельности мышцы непрерывно подстраиваются под внешнюю нагрузку. Но сохранение напряжения в мышечной ткани требует непрерывного подвода энергии. Расход энергии приводит к усталости мышц. Только обморок или смерть прерывают мышечные процессы.

Сосудистая ткань

Механические свойства кровеносных сосудов определяются, главным образом, свойствами коллагена, эластина и гладких мышечных волокон. Содержание этих составляющих сосудистой ткани изменяется по ходу кровеносной системы. С удалением от сердца увеличивается доля гладких мышечных волокон, в артериолах они уже являются основной составляющей сосудистой ткани.

Так как стенки кровеносных сосудов построены из высокоэластичного материала, то они способны к значительным обратимым изменениям размера при действии на них деформирующей силы. Деформирующая сила создается избыточным внутренним давлением.

Рассмотрим деформацию сосуда как результат действия давления изнутри на упругий цилиндр. Имеется часть цилиндрического кровеносного сосуда длины L, с толщиной стенок h и внутренним радиусом r. Сечения вдоль и поперек оси цилиндра показаны на рис. 6.17.

Две половинки сосуда взаимодействуют между собой по сечениям стенок цилиндра (заштрихованные области на рис. 6.17, а). Общая площадь сечения, вдоль которого взаимодействуют обе половинки сосуда, равна 2hL. Если в сосудистой стенке существует механическое напряжение σ, то сила взаимодействия двух половинок равна

Эта сила уравновешивается силами избыточного давления Р на цилиндр изнутри (они показаны стрелками на рис. 6.17, б). Силы направлены под разными углами к горизонтальной плоскости. Для того чтобы найти их равнодействующую, следует просуммировать

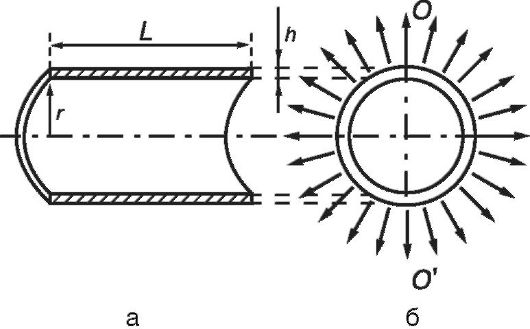Рис. 6.17. Сечения цилиндрического сосуда вдоль оси (а) и поперек оси (б)

горизонтальные проекции. Однако проще найти равнодействующую силу, если умножить давление на проекцию площади полуцилиндра на вертикальную плоскость ОО'. Эта проекция равна 2rL. Тогда выражение для силы через избыточное давление имеет вид

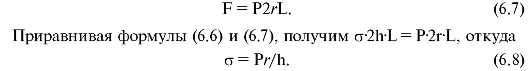Это соотношение называется уравнением Ламе.

Травма лица

Часто при повреждениях мягких тканей, особенно на открытых участках тела, в посттравматическом периоде применяют простые методы с использованием подручного материала. Так, для устранения асимметрии лица после травмы проводится лейкопластырное натяжение со здоровой стороны на больную (рис. 6.18).

Лейкопластырное натяжение направлено против тяги мышц здоровой кожи и осуществляется прочной фиксацией другого свободного конца пластыря к специальному шлему-маске, изготовленному индивидуально.

Рис. 6.18. Устранение асимметрии лица с помощью лейкопластыря.

В спортивной и космической медицине знание устойчивости различных биологических структур по отношению к различным деформациям играет главенствующую роль. В челюстно-лицевой хирургии, пластической хирургии и косметологии механические свойства тканей определяют объем воздействия и служат объективным критерием для оценки эффективности лечения. В травматологии и ортопедии вопросы механического воздействия на организм являются определяющими.

6.4. Механические модели

Вязкоупругие свойства тел (сочетание вязкого течения и высокой эластичности) моделируются системами, состоящими из различных комбинаций двух простых элементов: 1) пружины (упругий элемент) и 2) поршня с отверстиями, движущегося в цилиндре с вязкой жидкостью (вязкий элемент). Эти элементы и «конструируемые» с их помощью модели показаны на рис. 6.19 слева. Справа показаны зависимости деформации (ε) от времени при импульсном воздействии внешней силы: в момент времени t = 0 к телу, поведение которого моделируется, прикладывается постоянная сила F; в момент времени t₁ действие силы прекращается.

Моделью упругого тела является пружина (рис. 6.19, а), подчиняющаяся закону Гука. Деформация (ε) мгновенно появляется в момент t = 0 и мгновенно исчезает в момент t₁.

Моделью вязкого тела является поршень с отверстиями, движущийся в цилиндре с вязкой жидкостью (рис. 6.19, б). Связь между скоростью деформации вязкой среды (скоростью перемещения поршня) и напряжением имеет вид

Модель Максвелла

В модели Максвелла упругий и вязкий элементы соединены последовательно (рис. 6.19, в). Напряжение в каждом элементе является

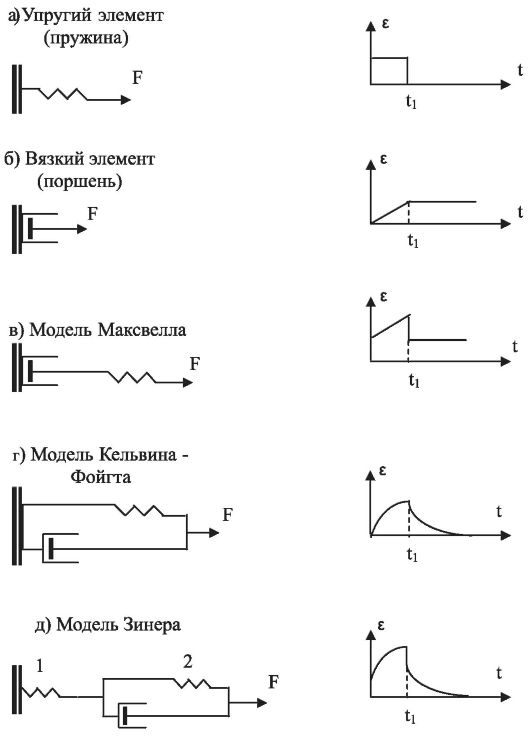Рис. 6.19. Механические модели вязкоупругих тел и динамика развития деформации

одинаковым. В любой момент времени для деформации выполняется условие

Решение этого уравнения приводит к следующему характеру развития деформации. В момент t = 0 пружина мгновенно растягивается, а затем начинается линейное нарастание деформации, связанное с движением поршня. В момент t₁ пружина сокращается до начального размера, а поршень останавливается - имеет место остаточная деформация.

С помощью модели Максвелла можно моделировать следующие механические процессы.

Релаксация напряжения в материале: ε = const, dε/dt = 0, т.е. поддерживается постоянная деформация. В этом случае из уравнения (6.10) следует

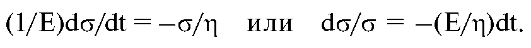Интегрируя последнее выражение от начального момента времени и начального напряжения σ_о до текущих значений t иσ, получаем выражение, описывающее изменение напряжения со временем, т.е. релаксацию напряжения:

т.е. под действием постоянной приложенной силы происходит вязкое течение (поршень движется с постоянной скоростью).

При изучении свойств волос используют явление релаксации напряжения в них. Этот процесс аппроксимируют моделью, состоящей из 4 параллельно соединенных моделей Максвелла.

Модель Кельвина-Фойгта

Модель Максвелла не учитывает упругости, отличной от той, которая подчиняется закону Гука, т.е. упругости, возникающей за счет раскручивания макромолекул (высокоэластичности). Основной особенностью этого вида упругости является необходимость известного промежутка времени для ее развития (аналогия - деформация пружины в вязкой среде). Такая «запаздывающая» упругая реакция представляется моделью Кельвина-Фойгта, в которой пружина и поршень соединены параллельно (рис. 6.19, г). Величина удлинения одинакова для обоих элементов. При воздействии внешней силы общее напряже-

Модель Зинера

В материалах реализуются разные виды деформаций: упругая обратимая (модель - пружина), вязкоупругая обратимая (модель Кельвина-Фойгта) и необратимая (модель - поршень). Сочетание трех моделей, рассмотренных выше, позволяет создавать модели, наиболее полно отражающие механические свойства тел и, в частности, биологических объектов.

Примером такой модели является модель Зинера (рис. 6.19, д), которая состоит из последовательно соединенных упругого элемента и модели Кельвина-Фойгта. Временная зависимость относительной

деформации (без вывода) показана на рис. 6.19, д. При действии постоянной нагрузки мгновенно растягивается пружина 1, затем вытягивается поршень и растягивается пружина 2, после прекращения нагрузки происходит быстрое сжатие пружины 1, а пружина 2 втягивает поршень в прежнее положение; остаточная деформация отсутствует.

Поведение костной ткани в первом приближении описывается моделью Зинера. Упругая деформация реализуется за счет минерального вещества, а ползучесть - за счет коллагена.

6.5. Основные понятия и формулы. Таблицы

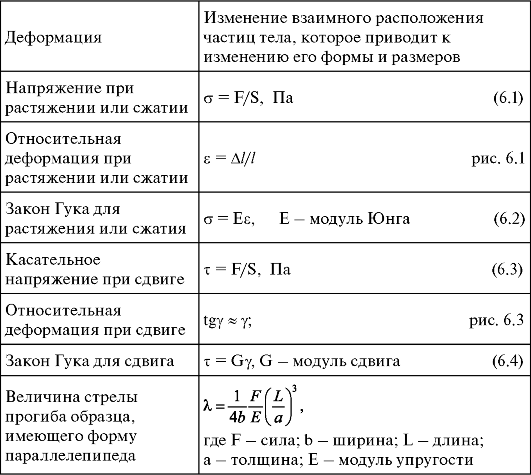Продолжение таблицы

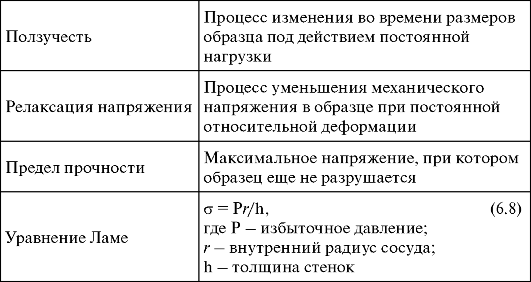Таблица 6.1. Модуль упругости (модуль Юнга) некоторых материалов

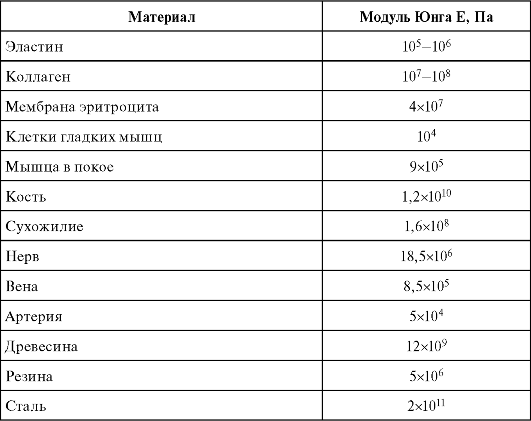Таблица 6.2. Прочностные характеристики различных тканей

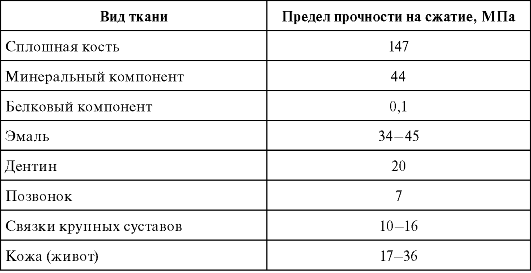Таблица 6.3. Проявление акустической анизотропии в коже

Окончание табл. 6.3

6.6. ЗАДАЧИ

1. Сухожилие длиной 16 см под действием силы 12,4 Н удлиняется на 3,3 мм. Сухожилие можно считать круглым в сечении с диаметром 8,6 мм. Рассчитать модуль упругости этого сухожилия.

3. Для определения механических свойств костной ткани была взята пластинка из свода черепа со следующими размерами: длина L = 5 см, ширина b = 1 см, толщина h = 0,5 см. Под действием силы F = 200 Н пластинка удлинилась на ΔL = 1,2х10^-3 см. Определить по этим данным модуль Юнга костной ткани при деформации растяжения.

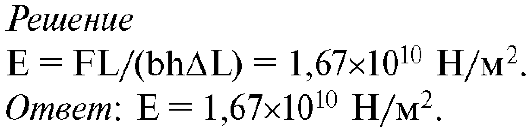4. Из большеберцовой кости собаки вырезали стержень прямоугольного сечения с ребрами а = 2 мм, b = 5 мм. Стержень положили на упоры, находящиеся на расстоянии L = 5 см друг от друга, и посередине между ними к нему приложили силу 28 Н. При этом стрела прогиба оказалась равной 1,5 мм. Определить модуль Юнга для этой кости.