Медицинская и биологическая физика. Курс лекций с задачами : учеб. пособие / В.Н. Федорова, Е.В. Фаустов. - 2008. - 592 с.
|
|
|
|
ЛЕКЦИЯ 1 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
1. Колебания. Периодические колебания. Гармонические колебания.
2. Свободные колебания. Незатухающие и затухающие колебания.
3. Вынужденные колебания. Резонанс.
4. Сопоставление колебательных процессов. Энергия незатухающих гармонических колебаний.
5. Автоколебания.
6. Колебания тела человека и их регистрация.
7. Основные понятия и формулы.
8. Задачи.
1.1. Колебания. Периодические колебания.
Гармонические колебания
Колебаниями называют процессы, отличающиеся той или иной степенью повторяемости.
Повторяющиеся процессы непрерывно происходят внутри любого живого организма, например: сокращения сердца, работа легких; мы дрожим, когда нам холодно; мы слышим и разговариваем благодаря колебаниям барабанных перепонок и голосовых связок; при ходьбе наши ноги совершают колебательные движения. Колеблются атомы, из которых мы состоим. Мир, в котором мы живем, удивительно склонен к колебаниям.
В зависимости от физической природы повторяющегося процесса различают колебания: механические, электрические и т.п. В настоящей лекции рассматриваются механические колебания.
Периодические колебания
Периодическими называют такие колебания, при которых все характеристики движения повторяются через определенный промежуток времени.
Для периодических колебаний используют следующие характеристики:
• период колебаний Т, равный времени, в течение которого совершается одно полное колебание;
• частота колебаний ν, равная числу колебаний, совершаемых за одну секунду (ν = 1/Т);
• амплитуда колебаний А, равная максимальному смещению от положения равновесия.
Гармонические колебания
Особое место среди периодических колебаний занимают гармонические колебания. Их значимость обусловлена следующими причинами. Во-первых, колебания в природе и в технике часто имеют характер, очень близкий к гармоническому, и, во-вторых, периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний.
Гармонические колебания - это колебания, при которых наблюдаемая величина изменяется во времени по закону синуса или косинуса:
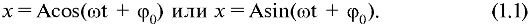 В математике функции этого вида называют гармоническими, поэтому колебания, описываемые такими функциями, тоже называют гармоническими.
В математике функции этого вида называют гармоническими, поэтому колебания, описываемые такими функциями, тоже называют гармоническими.
Положение тела, совершающего колебательное движение, характеризуется смещением относительно равновесного положения. В этом случае величины, входящие в формулу (1.1), имеют следующий смысл:
х - смещение тела в момент времени t;
А - амплитуда колебаний, равная максимальному смещению;
ω - круговая частота колебаний (число колебаний, совершаемых за 2π секунд), связанная с частотой колебаний соотношением
 φ = (ωt +φ0) - фаза колебаний (в момент времени t); φ0 - начальная фаза колебаний (при t = 0).
φ = (ωt +φ0) - фаза колебаний (в момент времени t); φ0 - начальная фаза колебаний (при t = 0).
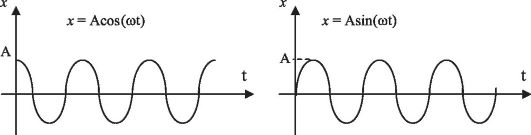 Рис. 1.1. Графики зависимости смещения от времени для х(0) = А и х(0) = 0
Рис. 1.1. Графики зависимости смещения от времени для х(0) = А и х(0) = 0
 1.2. Свободные колебания. Незатухающие и затухающие колебания
1.2. Свободные колебания. Незатухающие и затухающие колебания
Свободными или собственными называются такие колебания, которые происходят в системе, предоставленной самой себе, после того как она была выведена из положения равновесия.
Примером могут служить колебания шарика, подвешенного на нити. Для того чтобы вызвать колебания, нужно либо толкнуть шарик, либо, отведя в сторону, отпустить его. При толчке шарику сообщается кинетическая энергия, а при отклонении - потенциальная.
Свободные колебания совершаются за счет первоначального запаса энергии.
Свободные незатухающие колебания
Свободные колебания могут быть незатухающими только при отсутствии силы трения. В противном случае первоначальный запас энергии будет расходоваться на ее преодоление, и размах колебаний будет уменьшаться.
В качестве примера рассмотрим колебания тела, подвешенного на невесомой пружине, возникающие после того, как тело отклонили вниз, а затем отпустили (рис. 1.2).
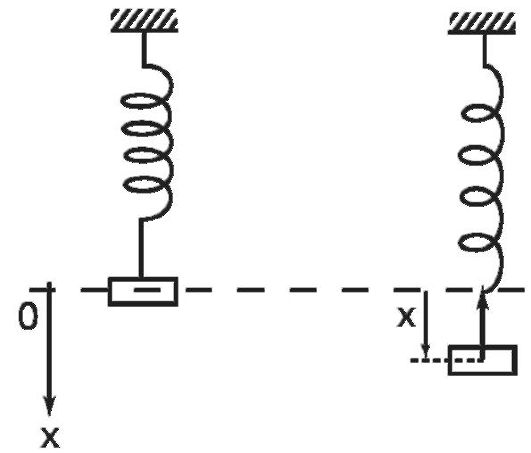 Рис. 1.2. Колебания тела на пружине
Рис. 1.2. Колебания тела на пружине
Со стороны растянутой пружины на тело действует упругая сила F, пропорциональная величине смещения х:
 Постоянный множитель k называется жесткостью пружины и
зависит от ее размеров и материала. Знак «-» указывает, что сила
упругости всегда направлена в сторону, противоположную направлению
смещения, т.е. к положению равновесия.
Постоянный множитель k называется жесткостью пружины и
зависит от ее размеров и материала. Знак «-» указывает, что сила
упругости всегда направлена в сторону, противоположную направлению
смещения, т.е. к положению равновесия.
При отсутствии трения упругая сила (1.4) - это единственная сила, действующая на тело. Согласно второму закону Ньютона (ma = F):
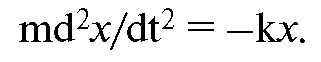 После
переноса всех слагаемых в левую часть и деления на массу тела (m)
получим дифференциальное уравнение свободных колебаний при отсутствии
трения:
После
переноса всех слагаемых в левую часть и деления на массу тела (m)
получим дифференциальное уравнение свободных колебаний при отсутствии
трения:
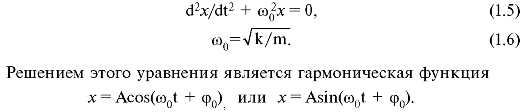 Величина ω0 (1.6) оказалась равной циклической частоте. Эту частоту называют собственной.
Величина ω0 (1.6) оказалась равной циклической частоте. Эту частоту называют собственной.
Таким образом, свободные колебания при отсутствии трения являются гармоническими, если при отклонении от положения равновесия возникает упругая сила (1.4).
Собственная круговая частота является основной характеристикой свободных гармонических колебаний. Эта величина зависит только от свойств колебательной системы (в рассматриваемом случае - от массы тела и жесткости пружины). В дальнейшем символ ω0 всегда будет использоваться для обозначения собственной круговой частоты (т.е. частоты, с которой происходили бы колебания при отсутствии силы трения).
Амплитуда свободных колебаний определяется свойствами колебательной системы (m, k) и энергией, сообщенной ей в начальный момент времени.
При отсутствии трения свободные колебания, близкие к гармоническим, возникают также и в других системах: математический и физический маятники (теория этих вопросов не рассматривается) (рис. 1.3).
Математический маятник - небольшое тело (материальная точка), подвешенное на невесомой нити (рис. 1.3 а). Если нить отклонить от положения равновесия на небольшой (до 5°) угол α и отпустить, то тело будет совершать колебания с периодом, определяемым по формуле
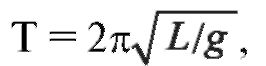 где L - длина нити, g - ускорение свободного падения.
где L - длина нити, g - ускорение свободного падения.
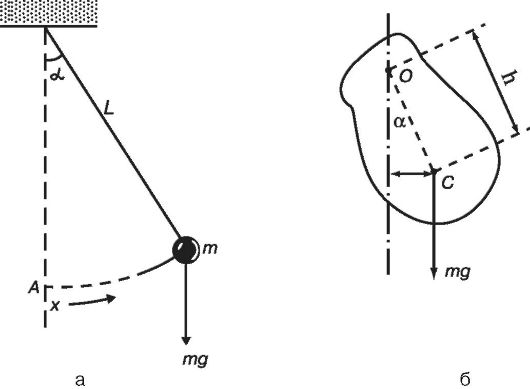 Рис. 1.3. Математический маятник (а), физический маятник (б)
Рис. 1.3. Математический маятник (а), физический маятник (б)
Физический маятник - твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси. На рисунке 1.3 б схематически изображен физический маятник в виде тела произвольной формы, отклоненного от положения равновесия на угол α. Период колебаний физического маятника описывается формулой
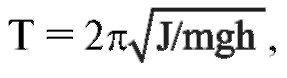 где
J - момент инерции тела относительно оси, m - масса, h - расстояние
между центром тяжести (точка С) и осью подвеса (точка О).
где
J - момент инерции тела относительно оси, m - масса, h - расстояние
между центром тяжести (точка С) и осью подвеса (точка О).
Момент инерции - это величина, зависящая от массы тела, его размеров и положения относительно оси вращения. Вычисляется момент инерции по специальным формулам.
Свободные затухающие колебания
Силы трения, действующие в реальных системах, существенно изменяют характер движения: энергия колебательной системы постоянно убывает, и колебания либо затухают, либо вообще не возникают.
Сила сопротивления направлена в сторону, противоположную движению тела, и при не очень больших скоростях пропорциональна величине скорости:
 График таких колебаний представлен на рис. 1.4.
График таких колебаний представлен на рис. 1.4.
В качестве характеристики степени затухания используют безразмерную величину, называемую логарифмическим декрементом затухания λ.
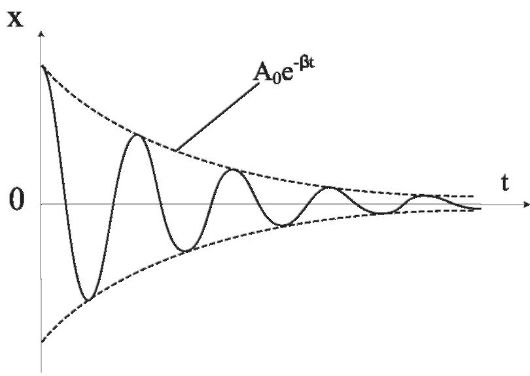 Рис. 1.4. Зависимость смещения от времени при затухающих колебаниях
Рис. 1.4. Зависимость смещения от времени при затухающих колебаниях
Логарифмический декремент затухания равен натуральному логарифму отношения амплитуды предыдущего колебания к амплитуде последующего колебания.
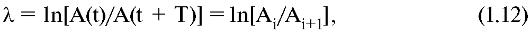 где i - порядковый номер колебания.
где i - порядковый номер колебания.
Нетрудно видеть, что логарифмический декремент затухания находится по формуле
 Сильное затухание. При
Сильное затухание. При
выполнении условия β ≥ ω0 система возвращается в положение равновесия, не совершая колебаний. Такое движение называется апериодическим. На рисунке 1.5 показаны два возможных способа возвращения в положение равновесия при апериодическом движении.
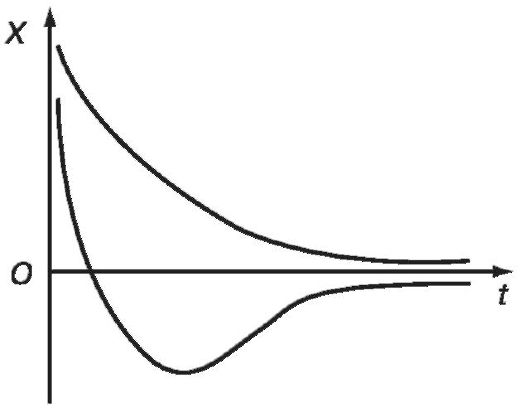 Рис. 1.5. Апериодическое движение
Рис. 1.5. Апериодическое движение
1.3. Вынужденные колебания, резонанс
Свободные колебания при наличии сил трения являются затухающими. Незатухающие колебания можно создать с помощью периодического внешнего воздействия.
Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодической силы (ее называют вынуждающей силой).
Пусть вынуждающая сила изменяется по гармоническому закону
 График вынужденных колебаний представлен на рис. 1.6.
График вынужденных колебаний представлен на рис. 1.6.
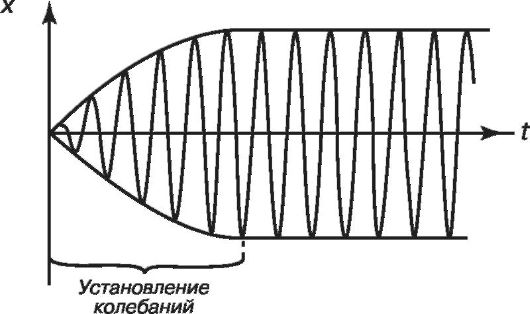 Рис. 1.6. График зависимости смещения от времени при вынужденных колебаниях
Рис. 1.6. График зависимости смещения от времени при вынужденных колебаниях
Видно, что амплитуда вынужденных колебаний достигает установившегося значения постепенно. Установившиеся вынужденные колебания являются гармоническими, а их частота равна частоте вынуждающей силы:
 Амплитуда (А) установившихся вынужденных колебаний находится по формуле:
Амплитуда (А) установившихся вынужденных колебаний находится по формуле:
 Резонансом называется достижение максимальной амплитуды вынужденных колебаний при определенном значении частоты вынуждающей силы.
Резонансом называется достижение максимальной амплитуды вынужденных колебаний при определенном значении частоты вынуждающей силы.
Если условие (1.18) не выполнено, то резонанс не возникает. В этом случае при увеличении частоты вынуждающей силы амплитуда вынужденных колебаний монотонно убывает, стремясь к нулю.
Графическая зависимость амплитуды А вынужденных колебаний от круговой частоты вынуждающей силы при разных значениях коэффициента затухания (β1 > β2 > β3) показана на рис. 1.7. Такая совокупность графиков называется резонансными кривыми.
В некоторых случаях сильное возрастание амплитуды колебаний при резонансе является опасным для прочности системы. Известны случаи, когда резонанс приводил к разрушению конструкций.
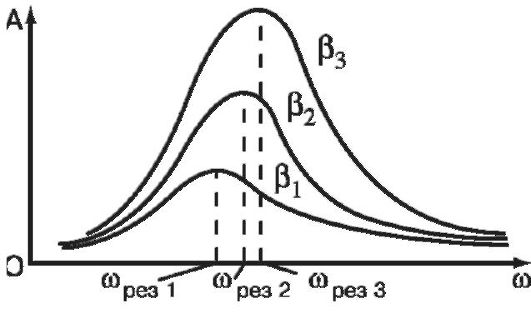 Рис. 1.7. Резонансные кривые
Рис. 1.7. Резонансные кривые
1.4. Сопоставление колебательных процессов. Энергия незатухающих гармонических колебаний
В таблице 1.1 представлены характеристики рассмотренных колебательных процессов.
Таблица 1.1. Характеристики свободных и вынужденных колебаний
 Энергия незатухающих гармонических колебаний
Энергия незатухающих гармонических колебаний
Тело, совершающее гармонические колебания, обладает двумя видами энергии: кинетической энергией движения Ек = mv2/2 и потенциальной энергией Еп, связанной с действием упругой силы. Известно, что при действии упругой силы (1.4) потенциальная энергия тела определяется формулой Еп = кх2/2. Для незатухающих колебаний х = А cos(ωt), а скорость тела определяется по формуле v = - А ωsin(ωt). Отсюда получаются выражения для энергий тела, совершающего незатухающие колебания:
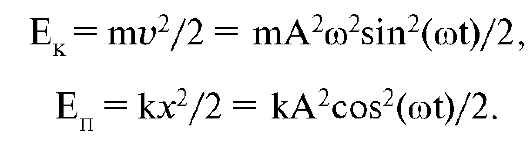 Полная
энергия системы, в которой происходят незатухающие гармонические
колебания, складывается из этих энергий и остается неизменной:
Полная
энергия системы, в которой происходят незатухающие гармонические
колебания, складывается из этих энергий и остается неизменной:
 Здесь m - масса тела, ω и A - круговая частота и амплитуда колебаний, k - коэффициент упругости.
Здесь m - масса тела, ω и A - круговая частота и амплитуда колебаний, k - коэффициент упругости.
1.5. Автоколебания
Существуют такие системы, которые сами регулируют периодическое восполнение потерянной энергии и поэтому могут колебаться длительное время.
Автоколебания - незатухающие колебания, поддерживаемые внешним источником энергии, поступление которой регулируется самой колебательной системой.
Системы, в которых возникают такие колебания, называются автоколебательными. Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы. Автоколебательную систему можно представить следующей схемой:
 В
данном случае сама колебательная система каналом обратной связи
воздействует на регулятор энергии, информируя его о состоянии системы.
В
данном случае сама колебательная система каналом обратной связи
воздействует на регулятор энергии, информируя его о состоянии системы.
Обратной связью называется воздействие результатов какоголибо процесса на его протекание.
Если такое воздействие приводит к возрастанию интенсивности процесса, то обратная связь называется положительной. Если воздействие приводит к уменьшению интенсивности процесса, то обратная связь называется отрицательной.
В автоколебательной системе может присутствовать как положительная, так и отрицательная обратная связь.
Примером автоколебательной системы являются часы, в которых маятник получает толчки за счет энергии поднятой гири или закрученной пружины, причем эти толчки происходят в те моменты, когда маятник проходит через среднее положение.
Примером биологических автоколебательных систем являются такие органы, как сердце, легкие.
1.6. Колебания тела человека и их регистрация
Aнализ колебаний, создаваемых телом человека или его отдельными частями, широко используется в медицинской практике.
Колебательные движения тела человека при ходьбе
Ходьба - это сложный периодический локомоторный процесс, возникающий в результате координированной деятельности скелетных мышц туловища и конечностей. Aнализ процесса ходьбы дает много диагностических признаков.
Характерной особенностью ходьбы является периодичность опорного положения одной ногой (период одиночной опоры) или двух ног (период двойной опоры). В норме соотношение этих периодов равно 4:1. При ходьбе происходит периодическое смещение центра масс (ЦМ) по вертикальной оси (в норме на 5 см) и отклонение в сторону (в норме на 2,5 см). При этом ЦМ совершает движение по кривой, которую приближенно можно представить гармонической функцией (рис. 1.8).
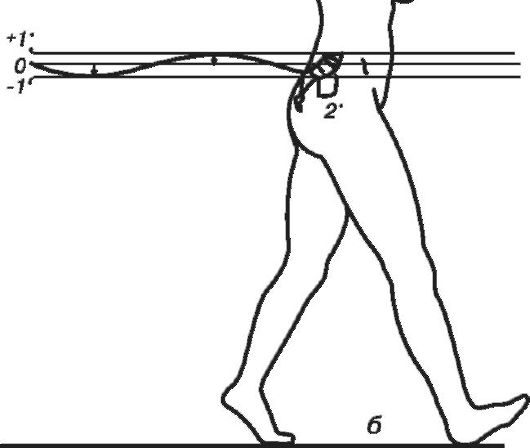 Рис. 1.8. Вертикальное смещение ЦМ тела человека во время ходьбы
Рис. 1.8. Вертикальное смещение ЦМ тела человека во время ходьбы
Сложные колебательные движения при поддержании вертикального положения тела.
У человека, стоящего вертикально, происходят сложные колебания общего центра масс (ОЦМ) и центра давления (ЦД) стоп на плоскость опоры. На анализе этих колебаний основана статокинезиметрия - метод оценки способности человека сохранять вертикальную позу. Посредством удержания проекции ОЦМ в пределах координат границы площади опоры. Данный метод реализуется с помощью стабилометрического анализатора, основной частью которого является стабилоплатформа, на которой в вертикальной позе находится испытуемый. Колебания, совершаемые ЦД испытуемого при поддержании вертикальной позы, передаются стабилоплатформе и регистрируются специальными тензодатчиками. Сигналы тензодатчиков передаются на регистрирующее устройство. При этом записывается статокинезиграмма - траектория перемещения ЦД испытуемого на горизонтальной плоскости в двумерной системе координат. По гармоническому спектру статокинезиграммы можно судить об особенностях вертикализации в норме и при отклонениях от нее. Данный метод позволяет анализировать показатели статокинетической устойчивости (СКУ) человека.
Механические колебания сердца
Существуют различные методы исследования сердца, в основе которых лежат механические периодические процессы.
Баллистокардиография (БКГ) - метод исследования механических проявлений сердечной деятельности, основанный на регистрации пульсовых микроперемещений тела, обусловленных выбрасыванием толчком крови из желудочков сердца в крупные сосуды. При этом возникает явление отдачи. Тело человека помещают на специальную подвижную платформу, находящуюся на массивном неподвижном столе. Платформа в результате отдачи приходит в сложное колебательное движение. Зависимость смещения платформы с телом от времени называется баллистокардиограммой (рис. 1.9), анализ которой позволяет судить о движении крови и состоянии сердечной деятельности.
Апекскардиография (AKГ) - метод графической регистрации низкочастотных колебаний грудной клетки в области верхушечного толчка, вызванных работой сердца. Регистрация апекскардиограммы производится, как правило, на многоканальном электрокарди-
 Рис. 1.9. Запись баллистокардиограммы
Рис. 1.9. Запись баллистокардиограммы
ографе при помощи пьезокристаллического датчика, являющегося преобразователем механических колебаний в электрические. Перед записью на передней стенке грудной клетки пальпаторно определяют точку максимальной пульсации (верхушечный толчок), в которой и фиксируют датчик. По сигналам датчика автоматически строится апекскардиограмма. Проводят амплитудный анализ АКГ - сравнивают амплитуды кривой при разных фазах работы сердца с максимальным отклонением от нулевой линии - отрезок ЕО, принимаемый за 100%. На рисунке 1.10 представлена апекскардиограмма.
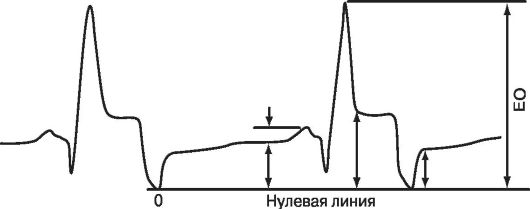 Рис. 1.10. Запись апекскардиограммы
Рис. 1.10. Запись апекскардиограммы
Кинетокардиография (ККГ) - метод регистрации низкочастотных вибраций стенки грудной клетки, обусловленных сердечной деятельностью. Кинетокардиограмма отличается от апекскардиограммы: первая фиксирует запись абсолютных движений грудной стенки в пространстве, вторая регистрирует колебания межреберий относительно ребер. В данном методе определяются перемещение (ККГх), скорость перемещения (ККГv) а также ускорение (ККГа) для колебаний грудной клетки. На рисунке 1.11 представлено сопоставление различных кинетокардиограмм.
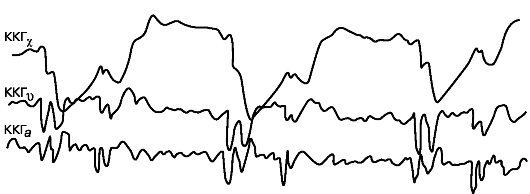 Рис. 1.11. Запись кинетокардиограмм перемещения (х), скорости (v), ускорения (а)
Рис. 1.11. Запись кинетокардиограмм перемещения (х), скорости (v), ускорения (а)
Динамокардиография (ДКГ) - метод оценки перемещения центра тяжести грудной клетки. Динамокардиограф позволяет регистрировать силы, действующие со стороны грудной клетки человека. Для записи динамокардиограммы пациент располагается на столе лежа на спине. Под грудной клеткой находится воспринимающее устройство, которое состоит из двух жестких металлических пластин размером 30x30 см, между которыми расположены упругие элементы с укрепленными на них тензодатчиками. Периодически меняющаяся по величине и месту приложения нагрузка, действующая на воспринимающее устройство, слагается из трех компонент: 1) постоянная составляющая - масса грудной клетки; 2) переменная - механический эффект дыхательных движений; 3) переменная - механические процессы, сопровождающие сердечное сокращение.
Запись динамокардиограммы осуществляют при задержке дыхания исследуемым в двух направлениях: относительно продольной и поперечной оси воспринимающего устройства. Сравнение различных динамокардиограмм показано на рис. 1.12.
Сейсмокардиография основана на регистрации механических колебаний тела человека, вызванных работой сердца. В этом методе с помощью датчиков, установленных в области основания мечевидного отростка, регистрируется сердечный толчок, обусловленный механической активностью сердца в период сокращения. При этом происходят процессы, связанные с деятельностью тканевых механорецепторов сосудистого русла, активирующихся при снижении объема циркулирующей крови. Сейсмокардиосигнал формирует форма колебаний грудины.
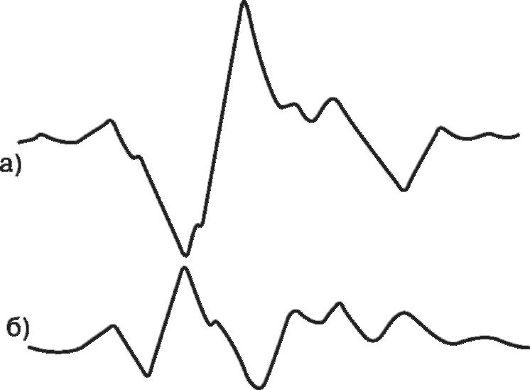 Рис. 1.12. Запись нормальной продольной (а) и поперечной (б) динамокардиограмм
Рис. 1.12. Запись нормальной продольной (а) и поперечной (б) динамокардиограмм
Вибрация
Широкое внедрение различных машин и механизмов в жизнь человека повышает производительность труда. Однако работа многих механизмов связана с возникновением вибраций, которые передаются человеку и оказывают на него вредное влияние.
Вибрация - вынужденные колебания тела, при которых либо все тело колеблется как единое целое, либо колеблются его отдельные части с различными амплитудами и частотами.
Человек постоянно испытывает различного рода вибрационные воздействия в транспорте, на производстве, в быту. Колебания, возникшие в каком-либо месте тела (например, руке рабочего, держащего отбойный молоток), распространяются по всему телу в виде упругих волн. Эти волны вызывают в тканях организма переменные деформации различных видов (сжатие, растяжение, сдвиг, изгиб). Действие вибраций на человека обусловлено многими факторами, характеризующими вибрации: частотой (спектр частот, основная частота), амплитудой, скоростью и ускорением колеблющейся точки, энергией колебательных процессов.
Продолжительное воздействие вибраций вызывает в организме стойкие нарушения нормальных физиологических функций. Может возникнуть «вибрационная болезнь». Эта болезнь приводит к ряду серьезных нарушений в организме человека.
Влияние, которое вибрации оказывают на организм, зависит от интенсивности, частоты, длительности вибраций, места их приложения и направления по отношению к телу, позе, а также от состояния человека и его индивидуальных особенностей.
Колебания с частотой 3-5 Гц вызывают реакции вестибулярного аппарата, сосудистые расстройства. При частотах 3-15 Гц наблюдаются расстройства, связанные с резонансными колебаниями отдельных органов (печень, желудок, голова) и тела в целом. Колебания с частотами 11-45 Гц вызывают ухудшение зрения, тошноту, рвоту. При частотах, превышающих 45 Гц, возникают повреждение сосудов головного мозга, нарушение циркуляции крови и т.д. На рисунке 1.13 приведены области частот вибрации, оказывающие вредное действие на человека и системы его органов.
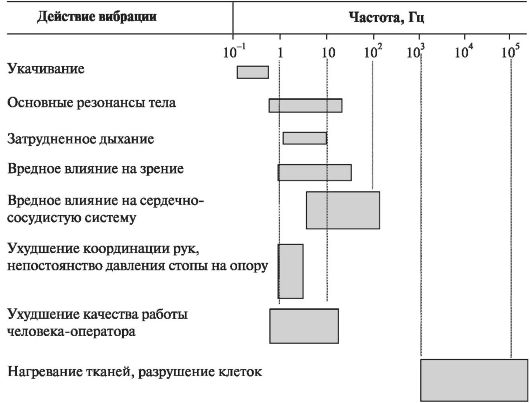 Рис. 1.13. Области частот вредного воздействия вибрации на человека
Рис. 1.13. Области частот вредного воздействия вибрации на человека
В то же время в ряде случаев вибрации находят применение в медицине. Например, при помощи специального вибратора стоматолог готовит амальгаму. Использование высокочастотных вибрационных аппаратов позволяет высверлить в зубе отверстие сложной формы.
Вибрация используется и при массаже. При ручном массаже массируемые ткани приводятся в колебательное движение при помощи рук массажиста. При аппаратном массаже используются вибраторы, в которых для передачи телу колебательных движений служат наконечники различной формы. Вибрационные аппараты подразделяются на аппараты для общей вибрации, вызывающие сотрясение всего тела (вибрационные «стул», «кровать», «платформа» и др.), и аппараты местного вибрационного воздействия на отдельные участки тела.
Механотерапия
В лечебной физкультуре (ЛФК) используются тренажеры, на которых осуществляются колебательные движения различных частей тела человека. Они используются в механотерапии - форме ЛФК, одной из задач которой является осуществление дозированных, ритмически повторяющихся физических упражнений с целью тренировки или восстановления подвижности в суставах на аппаратах маятникового типа. Основу этих аппаратов составляет балансирующий (от фр. balancer - качать, уравновешивать) маятник, который представляет собой двуплечный рычаг, совершающий колебательные (качательные) движения около неподвижной оси.
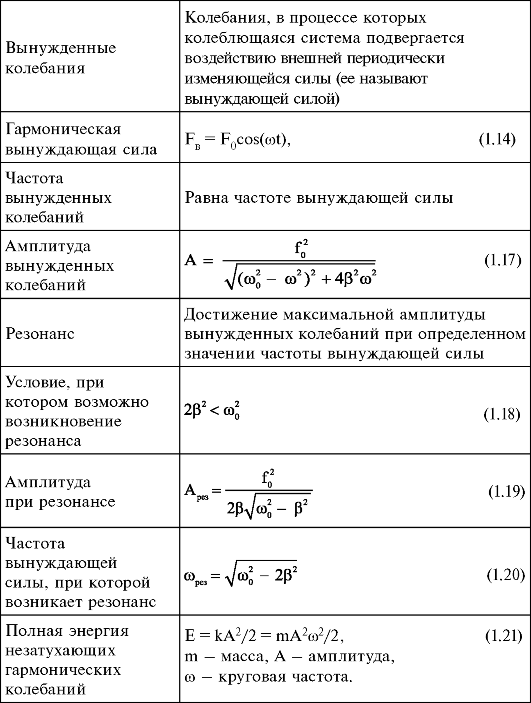
1.7. Основные понятия и формулы
 Продолжение таблицы
Продолжение таблицы
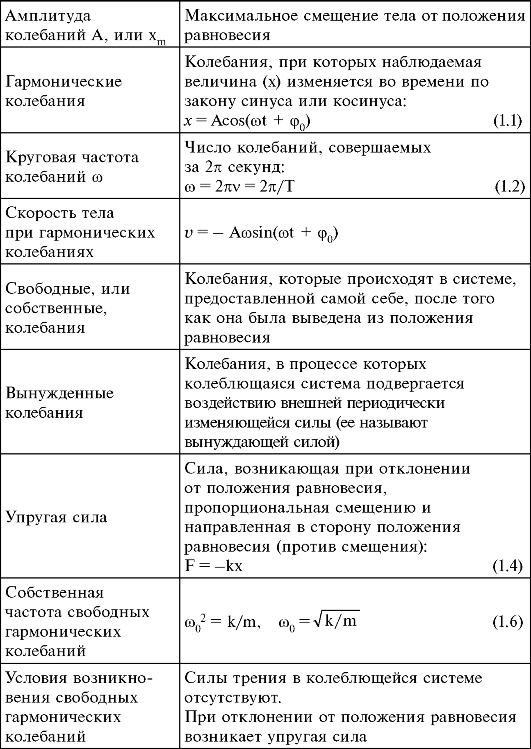 Продолжение таблицы
Продолжение таблицы
 Окончание таблицы
Окончание таблицы
 1.8. Задачи
1.8. Задачи
1. Привести примеры колебательных систем у человека.
2. У взрослого человека сердце делает 70 сокращений в минуту. Определить: а) частоту сокращений; б) число сокращений за 50 лет
жизни.
Ответ: а) 1,17 Гц; б) 1,84х109.
3. Какую длину должен иметь математический маятник, чтобы период его колебаний был равен 1 секунде?
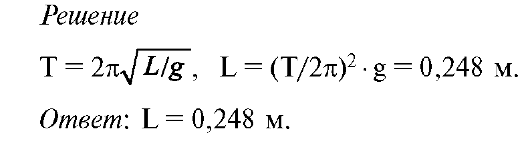 4. Тонкий
прямой однородный стержень длиной 1 м подвешен за конец на оси.
Определить: а) чему равен период его колебаний (малых)? б) какова длина
математического маятника, имеющего такой же период колебаний?
4. Тонкий
прямой однородный стержень длиной 1 м подвешен за конец на оси.
Определить: а) чему равен период его колебаний (малых)? б) какова длина
математического маятника, имеющего такой же период колебаний?
 5. Тело
массой 1 кг совершает колебания по закону х = 0,42 cos(7,40t), где t -
измеряется в секундах, а х - в метрах. Найти: а) амплитуду; б) частоту;
в) полную энергию; г) кинетическую и потенциальную энергии при х = 0,16
м.
5. Тело
массой 1 кг совершает колебания по закону х = 0,42 cos(7,40t), где t -
измеряется в секундах, а х - в метрах. Найти: а) амплитуду; б) частоту;
в) полную энергию; г) кинетическую и потенциальную энергии при х = 0,16
м.
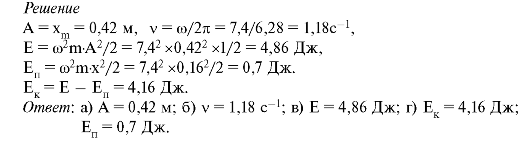 6. Оценить скорость, с которой идет человек при длине шага l =
0,65 м. Длина ноги L = 0,8 м; центр тяжести находится на расстоянии H =
0,5 м от ступни. Для момента инерции ноги относительно тазобедренного
сустава использовать формулу I = 0,2mL2.
6. Оценить скорость, с которой идет человек при длине шага l =
0,65 м. Длина ноги L = 0,8 м; центр тяжести находится на расстоянии H =
0,5 м от ступни. Для момента инерции ноги относительно тазобедренного
сустава использовать формулу I = 0,2mL2.
 7. Каким
образом можно определить массу небольшого тела на борту космической
станции, если в вашем распоряжении имеются часы, пружина и набор гирь?
7. Каким
образом можно определить массу небольшого тела на борту космической
станции, если в вашем распоряжении имеются часы, пружина и набор гирь?
 8. Амплитуда
затухающих колебаний убывает за 10 колебаний на 1/10 часть своей
первоначальной величины. Период колебаний Т = 0,4 с. Определить
логарифмический декремент и коэффициент затухания.
8. Амплитуда
затухающих колебаний убывает за 10 колебаний на 1/10 часть своей
первоначальной величины. Период колебаний Т = 0,4 с. Определить
логарифмический декремент и коэффициент затухания.