ЛЕКЦИЯ 23 ГЕОМЕТРИЧЕСКАЯ ОПТИКА

При решении многих задач, связанных с распространением света, можно использовать законы геометрической оптики, основанные на представлении о световом луче как линии, вдоль которой распространяется энергия световой волны. В однородной среде световые лучи прямолинейны. Геометрическая оптика - это предельный случай волновой оптики при стремлении длины волны к нулю (λ → 0).

23.1. Законы отражения и преломления света. Полное внутреннее отражение, световоды

Законы отражения

Отражение света - явление, происходящее на границе раздела двух сред, в результате которого световой луч изменяет направление своего распространения, оставаясь в первой среде. Характер отражения зависит от соотношения между размерами (h) неровностей отражающей поверхности и длиной волны (λ) падающего излучения.

Диффузное отражение

Когда неровности расположены хаотично, а их размеры имеют порядок длины волны или превышают ее, возникает диффузное отражение - рассеяние света по всевозможным направлениям. Именно вследствие диффузного отражения несамосветящиеся тела становятся видимыми при отражении света от их поверхностей.

Зеркальное отражение

Если размеры неровностей малы по сравнению с длиной волны (h << λ), то возникает направленное, или зеркальное, отражение света (рис. 23.1). При этом выполняются следующие законы.

Падающий луч, отраженный луч и нормаль к границе раздела двух сред, проведенная через точку падения луча, лежат в одной плоскости.

Угол отражения равен углу падения: β = a.

Рис. 23.1. Ход лучей при зеркальном отражении

Законы преломления

Когда световой луч падает на границу раздела двух прозрачных сред, он делится на два луча: отраженный и преломленный (рис. 23.2). Преломленный луч распространяется во второй среде, изменив свое направление. Оптической характеристикой среды является абсолютный

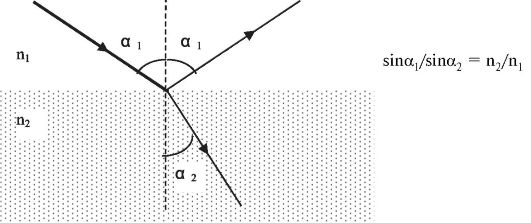Рис. 23.2. Ход лучей при преломлении

показатель преломления, который равен отношению скорости света в вакууме к скорости света в этой среде:

От соотношения показателей преломления двух сред и зависит направление преломленного луча. Выполняются следующие законы преломления.

Падающий луч, преломленный луч и нормаль к границе раздела двух сред, проведенная через точку падения луча, лежат в одной плоскости.

Отношение синуса угла падения к синусу угла преломления есть величина постоянная, равная отношению абсолютных показателей преломления второй и первой сред:

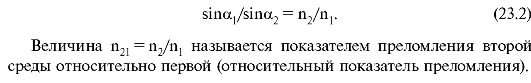23.2. Полное внутреннее отражение. Волоконная оптика

Рассмотрим переход света из среды c большим показателем преломления n₁ (оптически более плотной) в среду с меньшим показателем преломления n₂ (оптически менее плотную). На рисунке 23.3 показаны лучи, падающие на границу стекло-воздух. Для стекла показатель преломления n₁ = 1,52; для воздуха n₂ = 1,00.

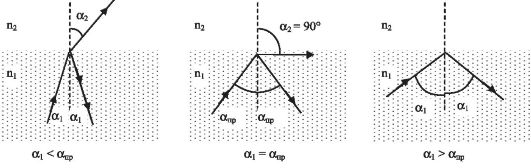Рис. 23.3. Возникновение полного внутреннего отражения (n₁ > n₂)

Увеличение угла падения приводит к увеличению угла преломления до тех пор, пока угол преломления не станет равным 90°. При дальнейшем увеличении угла падения падающий луч не преломляется, а полностью отражается от границы раздела. Это явление называется полным внутренним отражением. Оно наблюдается при падении света из более плотной среды на границу с менее плотной средой и состоит в следующем.

Если угол падения превышает предельный для данных сред угол, то преломления на границе раздела не происходит и падающий свет отражается полностью.

Предельный угол падения определяется соотношением

Сумма интенсивностей отраженного и преломленного лучей равна интенсивности падающего луча. При увеличении угла падения интенсивность отраженного луча растет, а интенсивность преломленного луча убывает и для предельного угла падения становится равной нулю.

Волоконная оптика

Явление полного внутреннего отражения используется в гибких световодах.

Если свет направить на торец тонкого стеклянного волокна, окруженного оболочкой с меньшим показателем преломления угла, то свет будет распространяться по волокну, испытывая полное отражение на границе стекло-оболочка. Такое волокно называется световодом. Изгибы световода не препятствуют прохождению света

(рис. 23.4).

В современных световодах потери света в результате его поглощения весьма малы (порядка 10 % на км), что позволяет использовать их в волоконно-оптических системах связи. В медицине жгуты из тонких световодов используют для изготовления эндоскопов, которые применяются для визуального исследования полых внутренних органов (рис. 23.5). Число волокон в эндоскопе достигает миллиона.

С помощью отдельного световодного канала, уложенного в общий жгут, осуществляется передача лазерного излучения с целью лечебного воздействия на внутренние органы.

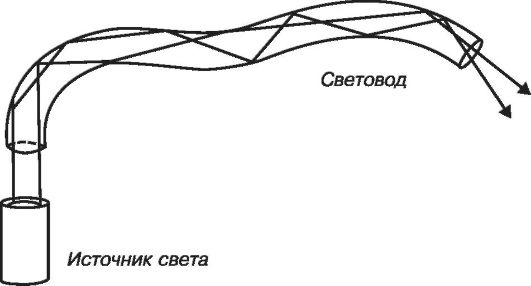Рис. 23.4. Распространение световых лучей по световоду

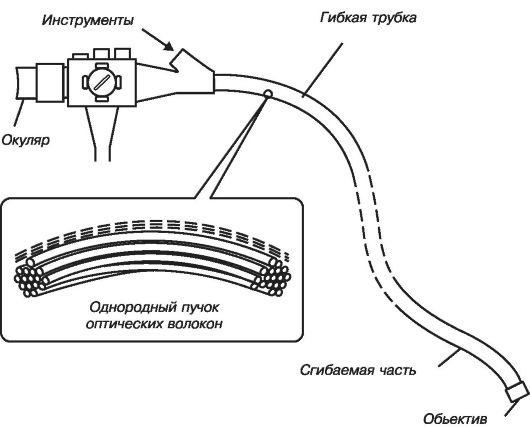Рис. 23.5. Эндоскоп

Существуют и природные световоды. Например, у травянистых растений стебель играет роль световода, подводящего свет в подземную часть растения. Клетки стебля образуют параллельные колонки, что напоминает конструкцию промышленных световодов. Если

освещать такую колонку, рассматривая ее через микроскоп, то видно, что ее стенки при этом остаются темными, а внутренность каждой клетки ярко освещена. Глубина, на которую доставляется таким способом свет, не превышает 4-5 см. Но и такого короткого световода достаточно, чтобы обеспечить светом подземную часть травянистого растения.

23.3. Линзы. Оптическая сила линзы

Линза - прозрачное тело, ограниченное обычно двумя сферическими поверхностями, каждая из которых может быть выпуклой или вогнутой. Прямая, проходящая через центры этих сфер, называется главной оптической осью линзы (слово главная обычно опускают).

Линза, максимальная толщина которой значительно меньше радиусов обеих сферических поверхностей, называется тонкой.

Проходя через линзу, световой луч изменяет направление - отклоняется. Если отклонение происходит в сторону оптической оси, то линза называется собирающей, в противном случае линза называется рассеивающей.

Любой луч, падающий на собирающую линзу параллельно оптической оси, после преломления проходит через точку оптической оси (F), называемую главным фокусом (рис. 23.6, а). Для рассеивающей линзы через фокус проходит продолжение преломленного луча (рис. 23.6, б).

У каждой линзы имеются два фокуса, расположенные по обе ее стороны. Расстояние от фокуса до центра линзы называется главным фокусным расстоянием (f).

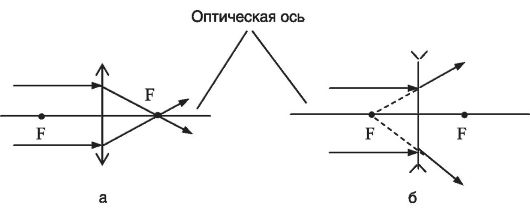Рис. 23.6. Фокус собирающей (а) и рассеивающей (б) линз

В расчетных формулах f берется со знаком «+» для собирающей линзы и со знаком «-» для рассеивающей линзы.

Величина, обратная фокусному расстоянию, называется оптической силой линзы: D = 1/f. Единица оптической силы - диоптрия (дптр). 1 дптр - это оптическая сила линзы с фокусным расстоянием 1 м.

Оптическая сила тонкой линзы и ее фокусное расстояние зависят от радиусов сфер и показателя преломления вещества линзы относительно окружающей среды:

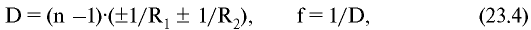где R₁, R₂ - радиусы кривизны поверхностей линзы; n - показатель преломления вещества линзы относительно окружающей среды; знак «+» берется для выпуклой поверхности, а знак «-» - для вогнутой. Одна из поверхностей может быть плоской. В этом случае принимают R = ∞, 1/R = 0.

Линзы используются для получения изображений. Рассмотрим предмет, расположенный перпендикулярно оптической оси собирающей линзы, и построим изображение его верхней точки А. Изображение всего предмета также будет перпендикулярно оси линзы. В зависимости от положения предмета относительно линзы возможны два случая преломления лучей, показанные на рис. 23.7.

1. Если расстояние от предмета до линзы превышает фокусное расстояние f, то лучи, испущенные точкой А, после прохождения линзы пересекаются в точке А', которая называется действительным изображением. Действительное изображение получается перевернутым.

2. Если расстояние от предмета до линзы меньше фокусного расстояния f, то лучи, испущенные точкой А, после прохождения линзы рас-

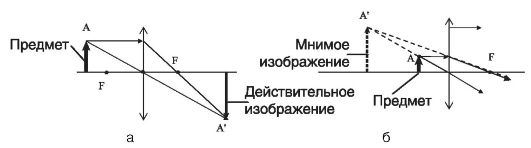Рис. 23.7. Действительное (а) и мнимое (б) изображения, даваемые собирающей линзой

ходятся и в точке А' пересекаются их продолжения. Эта точка называется мнимым изображением. Мнимое изображение получается прямым.

Рассеивающая линза дает мнимое изображение предмета при всех его положениях (рис. 23.8).

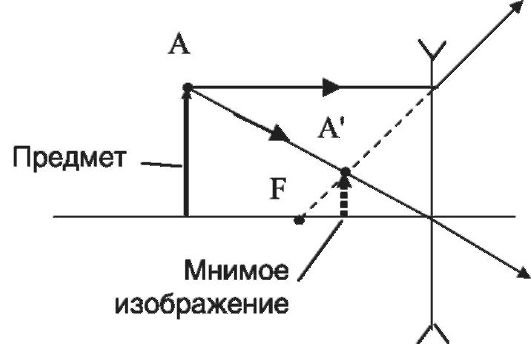Рис. 23.8. Мнимое изображение, даваемое рассеивающей линзой

Для расчета изображения используется формула линзы, которая устанавливает связь между положениями точки и ее изображения

(рис. 23.9):

где f - фокусное расстояние (для рассеивающей линзы оно отрицательно), a₁ - расстояние от предмета до линзы; a₂ - расстояние от изображения до линзы (знак «+» берется для действительного изображения, а знак «-» - для мнимого изображения).

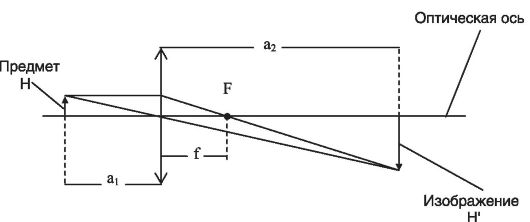Рис. 23.9. Параметры формулы линзы

Отношение размеров изображения к размерам предмета называется линейным увеличением:

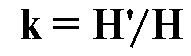Линейное увеличение рассчитывается по формуле k = а₂/а₁. Линза (даже тонкая) будет давать «правильное» изображение, подчиняющееся формуле линзы, только при выполнении следующих условий:

• пучки падающего света можно считать приосевыми (параксиальными);

• показатель преломления линзы не зависит от длины волны света или свет достаточно монохроматичен.

При получении с помощью линз изображений реальных предметов эти ограничения, как правило, не выполняются: имеет место дисперсия; некоторые точки предмета лежат в стороне от оптической оси; падающие световые пучки не являются параксиальными, линза не является тонкой. Все это приводит к искажению изображений. Для уменьшения искажений объективы оптических приборов изготавливают из нескольких линз, расположенных вплотную друг к другу. Оптическая сила такого объектива равна сумме оптических сил линз:

23.4. Аберрации линз

Аберрации - общее название для погрешностей изображения, возникающих при использовании линз. Аберрации (от лат. «aberratio» - отклонение), которые проявляются только в немонохроматическом свете, называются хроматическими. Все остальные виды аберраций являются монохроматическими, так как их проявление не связано со сложным спектральным составом реального света.

1. Сферическая аберрация - монохроматическая аберрация, обусловленная тем, что крайние (периферические) части линзы сильнее отклоняют лучи, идущие от точечного источника, чем ее центральная часть. В результате этого периферическая и центральная области линзы формируют различные изображения (S₂ и S'₂ соотвественно) точечного источника S₁ (рис. 23.10). Поэтому при любом положении экрана изображение на нем получается в виде светлого пятна.

Этот вид аберрации устраняется путем использования систем, состоящих из вогнутой и выпуклой линз.

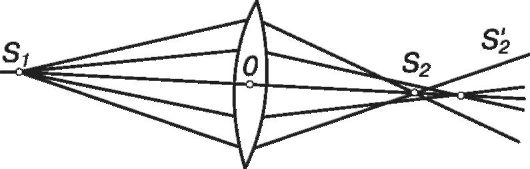Рис. 23.10. Сферическая аберрация

2. Астигматизм - монохроматическая аберрация, состоящая в том, что изображение точки имеет вид пятна эллиптической формы, которое при некоторых положениях плоскости изображения вырождается в отрезок.

Астигматизм косых пучков проявляется тогда, когда лучи, исходящие из точки, составляют значительные углы с оптической осью. На рисунке 23.11, а точечный источник расположен на побочной оптической оси. При этом возникают два изображения в виде отрезков прямых линий, расположенных перпендикулярно друг другу в плоскостях I и II. Изображение источника можно получить лишь в виде расплывчатого пятна между плоскостями I и II.

Астигматизм, обусловленный асимметрией оптической системы. Этот вид астигматизма возникает, когда симметрия оптической системы по отношению к пучку света нарушена в силу устройства самой системы. При такой аберрации линзы создают изображение, в котором контуры и линии, ориентированные в разных направлениях, имеют разную резкость. Это наблюдается в цилиндрических линзах (рис. 23.11, б).

Цилиндрическая линза образует линейное изображение точечного объекта.

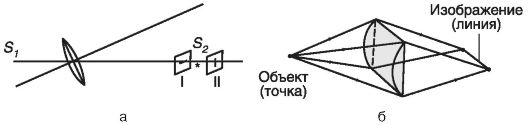Рис. 23.11. Астигматизм: косых пучков (а); обусловленный цилиндричностью линзы (б)

В глазу астигматизм образуется при асимметрии в кривизне систем хрусталика и роговицы. Для исправления астигматизма служат очки, которые имеют различную кривизну в разных направлениях.

3. Дисторсия (искажение). Когда лучи, посылаемые предметом, составляют большой угол с оптической осью, обнаруживается еще один вид монохроматической аберрации - дисторсия. В этом случае нарушается геометрическое подобие между объектом и изображением. Причина состоит в том, что в действительности линейное увеличение, даваемое линзой, зависит от угла падения лучей. В результате изображение квадратной сетки принимает либо подушко-, либо бочкообразный вид (рис. 23.12).

Для борьбы с дисторсией подбирают систему линз с противоположной дисторсией.

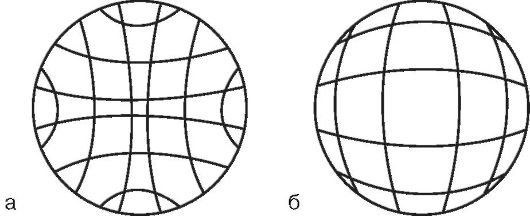Рис. 23.12. Дисторсия: а - подушкообразная, б - бочкообразная

4. Хроматическая аберрация проявляется в том, что пучок белого света, исходящий из точки, дает ее изображение в виде радужного круга, фиолетовые лучи пересекаются ближе к линзе, чем красные (рис. 23.13).

Причина хроматической аберрации заключается в зависимости показателя преломления вещества от длины волны падающего света (дисперсия). Для исправления этой аберрации в оптике используют линзы, изготавливаемые из стекол с разной дисперсией (ахроматы, апохроматы).

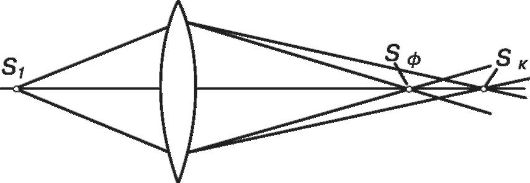Рис. 23.13. Хроматическая аберрация

23.5. Основные понятия и формулы

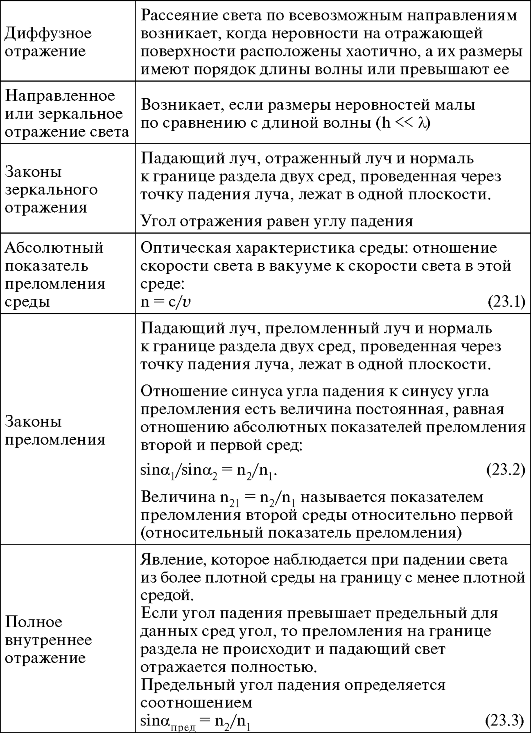Продолжение таблицы

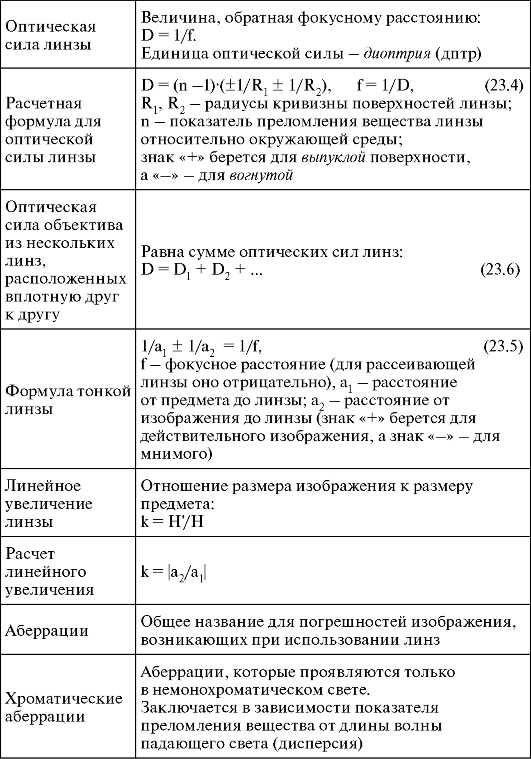Окончание таблицы

23.6. Задачи

1. Почему блестят воздушные пузыри в воде?

Ответ: за счет отражения света на границе «вода-воздух».

2. Почему в тонкостенном стакане с водой ложечка кажется увеличенной?

Ответ: вода в стакане выполняет роль цилиндрической собирающей линзы. Мы видим мнимое увеличенное изображение.

3. Оптическая сила линзы составляет 3 дптр. Чему равно фокусное расстояние линзы? Ответ выразить в см.

Решение

D = 1/f, f = 1/D = 1/3 = 0,33 м. Ответ: f = 33 см.

4. Фокусные расстояния у двух линз равны соответственно: f = +40 см, f₂ = -40 см. Найти их оптические силы.

6. Каким образом в ясную погоду можно определить фокусное расстояние собирающей линзы?

Решение

Расстояние от Солнца до Земли столь велико, что все лучи, падающие на линзу, параллельны друг другу. Если на экране получить изображение Солнца, то расстояние от линзы до экрана будет равно фокусному расстоянию.

7. Для линзы с фокусным расстоянием, равным 20 см, найти расстояния до объекта, при которых линейный размер действительного изображения будет: а) вдвое больше, чем размер объекта; б) равен размеру объекта; в) вдвое меньше, чем размер объекта.

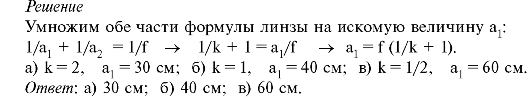8. Оптическая сила хрусталика для человека с нормальным зрением равна 25 дптр. Показатель преломления 1,4. Вычислить радиусы кривизны хрусталика, если известно, что один радиус кривизны в 2 раза больше другого.