ЛЕКЦИЯ 21 ДИФРАКЦИЯ СВЕТА

1. Дифракция света. Принцип Гюйгенса-Френеля.

2. Дифракция света на щели в параллельных лучах.

3. Дифракционная решетка.

4. Дифракционный спектр.

5. Характеристики дифракционной решетки как спектрального прибора.

6. Рентгеноструктурный анализ.

7. Дифракция света на круглом отверстии. Разрешающая способность диафрагмы.

8. Основные понятия и формулы.

9. Задачи.

В узком, но наиболее употребительном смысле, дифракция света - это огибание лучами света границы непрозрачных тел, проникновение света в область геометрической тени. В явлениях, связанных с дифракцией, имеет место существенное отклонение поведения света от законов геометрической оптики. (Дифракция проявляется не только для света.)

Дифракция - волновое явление, которое наиболее отчетливо проявляется в том случае, когда размеры препятствия соизмеримы (одного порядка) с длиной волны света. С малостью длин видимого света связано достаточно позднее обнаружение дифракции света (16-17 вв.).

21.1. Дифракция света. Принцип Гюйгенса-Френеля

Дифракцией света называется комплекс явлений, которые обусловлены его волновой природой и наблюдаются при распространении света в среде с резкими неоднородностями.

Качественное объяснение дифракции дает принцип Гюйгенса, который устанавливает способ построения фронта волны в момент времени t + Δt если известно его положение в момент времени t.

1. Согласно принципу Гюйгенса, каждая точка волнового фронта является центром когерентных вторичных волн. Огибающая этих волн дает положение фронта волны в следующий момент времени.

Поясним применение принципа Гюйгенса на следующем примере. Пусть на преграду с отверстием падает плоская волна, фронт которой параллелен преграде (рис. 21.1).

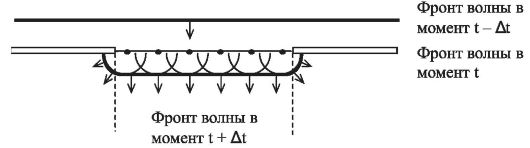Рис. 21.1. Пояснение принципа Гюйгенса

Каждая точка волнового фронта, выделяемого отверстием, служит центром вторичных сферических волн. На рисунке видно, что огибающая этих волн проникает в область геометрической тени, границы которой помечены штриховой линией.

Принцип Гюйгенса ничего не говорит об интенсивности вторичных волн. Этот недостаток был устранен Френелем, который дополнил принцип Гюйгенса представлением об интерференции вторичных волн и их амплитудах. Дополненный таким образом принцип Гюйгенса получил название принципа Гюйгенса-Френеля.

2. Согласно принципу Гюйгенса-Фре- неля величина световых колебаний в некоторой точке О есть результат интерференции в этой точке когерентных вторичных волн, испускаемых всеми элементами волновой поверхности. Амплитуда каждой вторичной волны пропорциональна площади элемента dS, обратно пропорциональна расстоянию r до точки О и убывает при возрастании угла α между нормалью n к элементу dS и направлением на точку О (рис. 21.2).

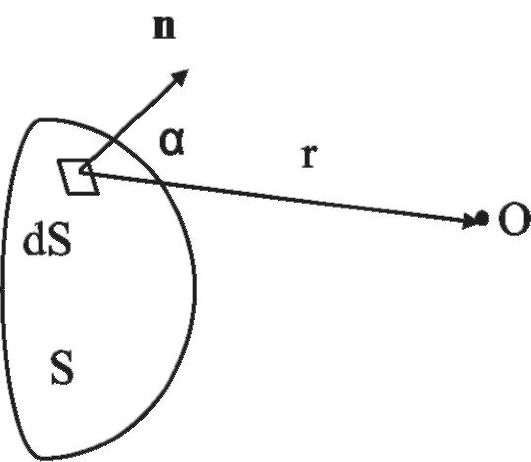Рис. 21.2. Испускание вторичных волн элементами волновой поверхности

21.2. Дифракция на щели в параллельных лучах

Вычисления, связанные с применением принципа Гюйгенса- Френеля, в общем случае представляют собой сложную математическую задачу. Однако в ряде случаев, обладающих высокой степенью симметрии, нахождение амплитуды результирующих колебаний может быть выполнено алгебраическим или геометрическим суммированием. Продемонстрируем это путем расчета дифракции света на щели.

Пусть на узкую щель (АВ) в непрозрачной преграде падает плоская монохроматическая световая волна, направление распространения которой перпендикулярно поверхности щели (рис. 21.3, а). За щелью (параллельно ее плоскости) поместим собирающую линзу, в фокальной плоскости которой расположим экран Э. Все вторичные волны, испускаемые с поверхности щели в направлении, параллельном оптической оси линзы (α = 0), приходят в фокус линзы в одинаковой фазе. Поэтому в центре экрана (O) имеет место максимум интерференции для волн любой длины. Его называют максимумом нулевого порядка.

Для того чтобы выяснить характер интерференции вторичных волн, испущенных в других направлениях, разобьем поверхность щели на n одинаковых зон (их называют зонами Френеля) и рассмотрим то направление, для которого выполняется условие:

где b - ширина щели, а λ - длина световой волны.

Лучи вторичных световых волн, идущие в этом направлении, пересекутся в точке О'.

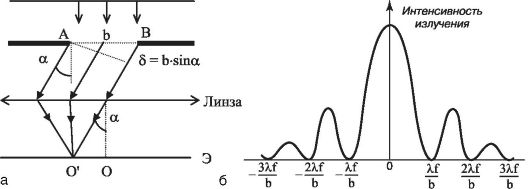Рис. 21.3. Дифракция на одной щели: а - ход лучей; б - распределение интенсивности света (f - фокусное расстояние линзы)

Произведение bsina равно разности хода (δ) между лучами, идущими от краев щели. Тогда разность хода лучей, идущих от соседних зон Френеля, равна λ/2 (см. формулу 21.1). Такие лучи при интерференции взаимно уничтожаются, так как они имеют одинаковые амплитуды и противоположные фазы. Рассмотрим два случая.

1) n = 2k - четное число. В этом случае происходит попарное гашение лучей от всех зон Френеля и в точке О' наблюдается минимум интерференционной картины.

Минимум интенсивности при дифракции на щели наблюдается для направлений лучей вторичных волн, удовлетворяющих условию

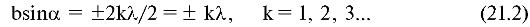Целое число k называется порядком минимума.

2) n = 2k - 1 - нечетное число. В этом случае излучение одной зоны Френеля останется непогашенным и в точке О' будет наблюдаться максимум интерференционной картины.

Максимум интенсивности при дифракции на щели наблюдается для направлений лучей вторичных волн, удовлетворяющих условию:

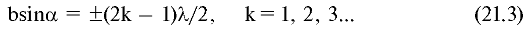Целое число k называется порядком максимума. Напомним, что для направления α = 0 имеет место максимум нулевого порядка.

Из формулы (21.3) следует, что при увеличении длины световой волны угол, под которым наблюдается максимум порядка k > 0, возрастает. Это означает, что для одного и того же k ближе всего к центру экрана располагается фиолетовая полоса, а дальше всего - красная.

На рисунке 21.3, б показано распределение интенсивности света на экране в зависимости от расстояния до его центра. Основная часть световой энергии сосредоточена в центральном максимуме. При увеличении порядка максимума его интенсивность быстро уменьшается. Расчеты показывают, что I₀:I₁:I₂= 1:0,047:0,017.

Если щель освещена белым светом, то на экране центральный максимум будет белым (он общий для всех длин волн). Побочные максимумы будут состоять из цветных полос.

Явление, подобное дифракции на щели, можно наблюдать на лезвии бритвы.

21.3. Дифракционная решетка

При дифракции на щели интенсивности максимумов порядка k > 0 столь незначительны, что не могут быть использованы для решения практических задач. Поэтому в качестве спектрального прибора используется дифракционная решетка, которая представляет собой систему параллельных равноотстоящих щелей. Дифракционную решетку можно получить нанесением непрозрачных штрихов (царапин) на плоскопараллельную стеклянную пластину (рис. 21.4). Пространство между штрихами (щели) пропускает свет.

Штрихи наносятся на поверхность решетки алмазным резцом. Их плотность достигает 2000 штрихов на миллиметр. При этом ширина решетки может быть до 300 мм. Общее число щелей решетки обозначается N.

Расстояние d между центрами или краями соседних щелей называют постоянной (периодом) дифракционной решетки.

Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей.

Ход лучей в дифракционной решетке представлен на рис. 21.5.

Пусть на решетку падает плоская монохроматическая световая волна, направление распространения которой перпендикулярно плоскости решетки. Тогда поверхности щелей принадлежат одной волновой поверхности и являются источниками когерентных вторичных волн. Рассмотрим вторичные волны, направление распространения которых удовлетворяет условию

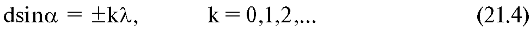После прохождения линзы лучи этих волн пересекутся в точке О'.

Произведение dsina равно разности хода (δ) между лучами, идущими от краев соседних щелей. При выполнении условия (21.4) вторичные волны приходят в точку О' в одинаковой фазе и на экране возникает максимум интерференционной картины. Максимумы, удовлетворяющие условию (21.4), называются главными максимумами порядка k. Само условие (21.4) называют основной формулой дифракционной решетки.

Главные максимумы при дифракции на решетке наблюдаются для направлений лучей вторичных волн, удовлетворяющих условию: dsinα = ± κλ; k = 0,1,2,...

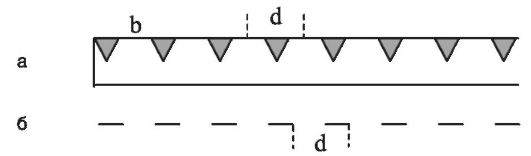Рис. 21.4. Сечение дифракционной решетки (а) и ее условное обозначение (б)

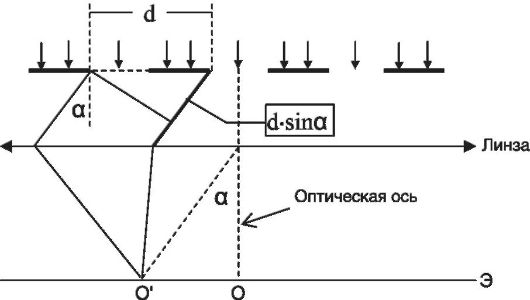Рис. 21.5. Дифракция света на дифракционной решетке

По ряду причин, которые здесь не рассматриваются, между главными максимумами располагаются (N - 2) добавочных максимумов. При большом числе щелей их интенсивность ничтожно мала и все пространство между главными максимумами выглядит темным.

Условие (21.4), определяющее положения всех главных максимумов, не учитывает дифракцию на отдельной щели. Может получиться так, что для некоторого направления будут одновременно выполняться условие максимума для решетки (21.4) и условие минимума для щели (21.2). В этом случае соответствующий главный максимум не возникает (формально он есть, но его интенсивность равна нулю).

Чем больше число щелей в дифракционной решетке (N), тем большее количество световой энергии проходит через решетку, тем более интенсивными и более острыми будут максимумы. На рисунке 21.6 представлены графики распределения интенсивностей, полученные от решеток с разным числом щелей (N). Периоды (d) и ширина щелей (b) у всех решеток одинаковы.

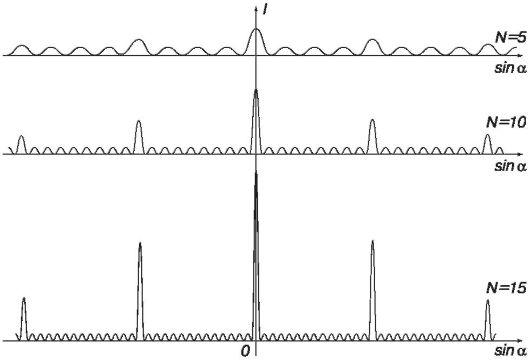Рис. 21.6. Распределение интенсивностей при разных значениях N

21.4. Дифракционный спектр

Из основной формулы дифракционной решетки (21.4) видно, что угол дифракции α, под которым образуются главные максимумы, зависит от длины волны падающего света. Поэтому максимумы интенсивности, соответствующие различным длинам волн, получаются в различных местах экрана. Это и позволяет использовать решетку как спектральный прибор.

Дифракционный спектр - спектр, полученный с помощью дифракционной решетки.

При падении на дифракционную решетку белого света все максимумы, кроме центрального, разложатся в спектр. Положение максимума порядка k для света с длиной волны λ определяется формулой:

Чем больше длина волны (λ), тем дальше от центра отстоит k-й максимум. Поэтому фиолетовая область каждого главного максимума будет обращена к центру дифракционной картины, а красная - наружу. Заметим, что при разложении белого света призмой сильнее отклоняются фиолетовые лучи.

Записывая основную формулу решетки (21.4), мы указали, что k - целое число. Насколько велико оно может быть? Ответ на этот вопрос дает неравенство |sinα| < 1. Из формулы (21.5) найдем

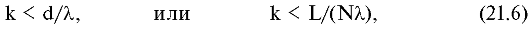где L - ширина решетки, а N - число штрихов.

Например, для решетки с плотностью 500 штрихов на мм d = 1/500 мм = 2х10^-6 м. Для зеленого света с λ = 520 нм = 520х10^-9 м получим k < 2х10^-6/(520 х10^-9) < 3,8. Таким образом, для такой решетки (весьма средней) порядок наблюдаемого максимума не превышает 3.

21.5. Характеристики дифракционной решетки как спектрального прибора

Основная формула дифракционной решетки (21.4) позволяет определить длину волны света, измеряя угол α, соответствующий положению k-го максимума. Таким образом, дифракционная решетка позволяет получать и анализировать спектры сложного света.

Спектральные характеристики решетки

Угловая дисперсия - величина, равная отношению изменения угла, под которым наблюдается дифракционный максимум, к изменению длины волны:

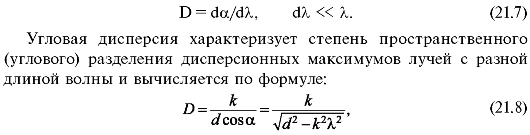где k - порядок максимума, α - угол, под которым он наблюдается.

Угловая дисперсия тем выше, чем больше порядок k спектра и чем меньше период решетки (d).

Разрешающая способность (разрешающая сила) дифракционной решетки - величина, характеризующая ее способность давать

где k - порядок максимума, а N - число штрихов решетки.

Из формулы видно, что близкие линии, которые сливаются в спектре первого порядка, могут восприниматься отдельно в спектрах второго или третьего порядков.

21.6. Рентгеноструктурный анализ

Основная формула дифракционной решетки может быть использована не только для определения длины волны, но и для решения обратной задачи - нахождения постоянной дифракционной решетки по известной длине волны.

В качестве дифракционной решетки можно взять структурную решетку кристалла. Если на простую кристаллическую решетку направить поток рентгеновских лучей под некоторым углом θ (рис. 21.7), то они будут дифрагировать, так как расстояние между рассеивающими центрами (атомами) в кристалле соответствует

длине волны рентгеновского излучения. Если на некотором расстоянии от кристалла поместить фотопластинку, то она зарегистрирует интерференцию отраженных лучей.

где d - межплоскостное расстояние в кристалле, θ - угол между плоскостью

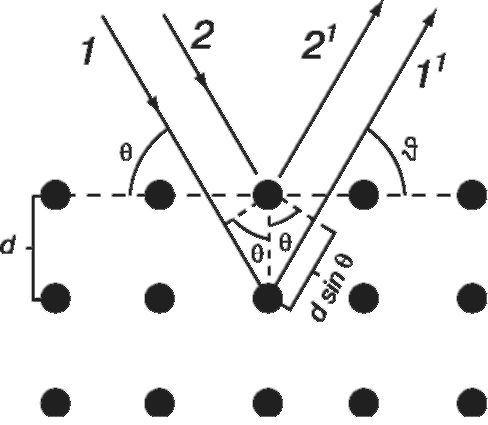Рис. 21.7. Дифракция рентгеновских лучей на простой кристаллической решетке; точками указано расположение атомов

кристалла и падающим рентгеновским лучом (угол скольжения), λ - длина волны рентгеновского излучения. Соотношение (21.11) называется условием Брэгга-Вульфа.

Если известна длина волны рентгеновского излучения и измерен угол θ, отвечающий условию (21.11), то можно определить межплоскостное (межатомное) расстояние d. На этом основан рентгеноструктурный анализ.

Рентгеноструктурный анализ - метод определения структуры вещества путем исследования закономерностей дифракции рентгеновского излучения на изучаемых образцах.

Рентгеновские дифракционные картины очень сложны, так как кристалл представляет собой трехмерный объект и рентгеновские лучи могут дифрагировать на различных плоскостях под разными углами. Если вещество представляет собой монокристалл, то дифракционная картина представляет собой чередование темных (засвеченных) и светлых (незасвеченных) пятен (рис. 21.8, а).

В том случае когда вещество представляет собой смесь большого числа очень маленьких кристалликов (как в металле или порошке), возникает серия колец (рис. 21.8, б). Каждое кольцо соответствует дифракционному максимуму определенного порядка k, при этом рентгенограмма образуется в виде окружностей (рис. 21.8, б).

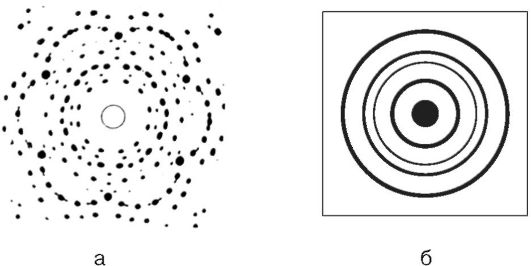Рис. 21.8. Рентгенограмма для монокристалла (а), рентгенограмма для поликристалла (б)

Рентгеноструктурный анализ используют и для исследования структур биологических систем. Например, этим методом была установлена структура ДНК.

21.7. Дифракция света на круглом отверстии. Разрешающая способность диафрагмы

В заключение рассмотрим вопрос о дифракции света на круглом отверстии, который представляет большой практический интерес. Такими отверстиями являются, например, зрачок глаза и объектив микроскопа. Пусть на линзу падает свет от точечного источника. Линза является отверстием, которое пропускает только часть световой волны. Вследствие дифракции на экране, расположенном за линзой, возникнет дифракционная картина, показанная на рис. 21.9, а.

Как и для щели, интенсивности побочных максимумов малы. Центральный максимум в виде светлого кружка (дифракционное пятно) и является изображением светящейся точки.

Диаметр дифракционного пятна определяется формулой:

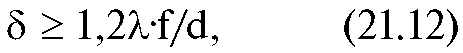где f - фокусное расстояние линзы, а d - ее диаметр.

Если на отверстие (диафрагму) падает свет от двух точечных источников, то в зависимости от углового расстояния между ними (β) их дифракционные пятна могут восприниматься раздельно (рис. 21.9, б) или сливаться (рис. 21.9, в).

Приведем без вывода формулу, которая обеспечивает раздельное изображение близких точечных источников на экране (разрешающая способность диафрагмы):

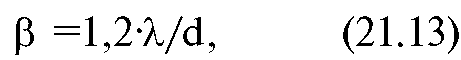где λ - длина волны падающего света, d - диаметр отверстия (диафрагмы), β - угловое расстояние между источниками.

Рис. 21.9. Дифракция на круглом отверстии от двух точечных источников

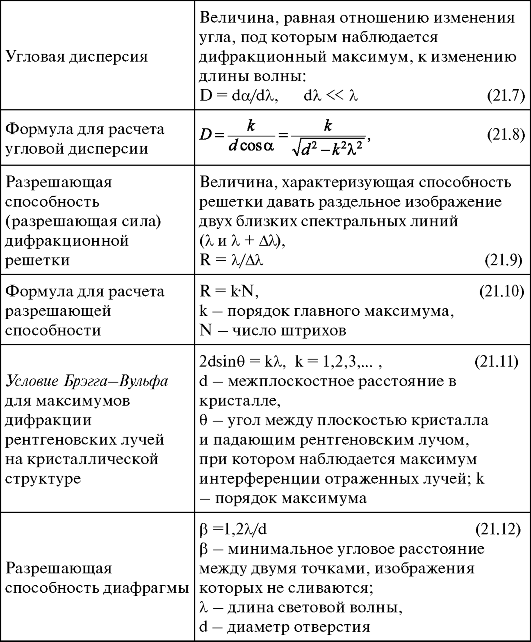
21.8. Основные понятия и формулы

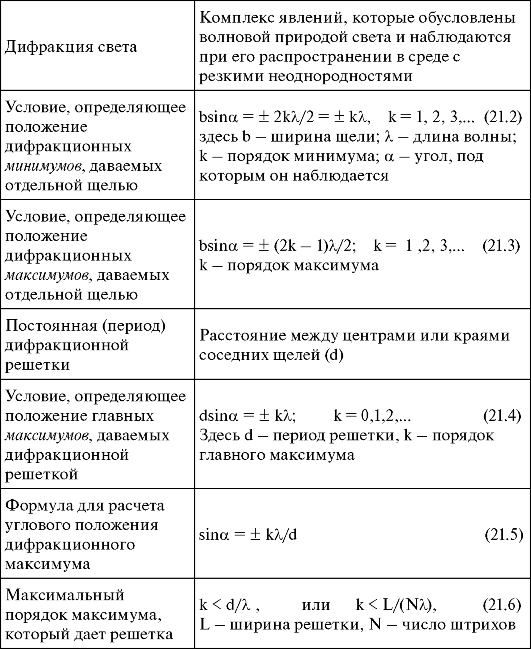Окончание таблицы

21.9. Задачи

1. Длина волны света, падающего на щель перпендикулярно ее плоскости, укладывается в ширине щели 6 раз. Под каким углом будет виден 3 дифракционный минимум?

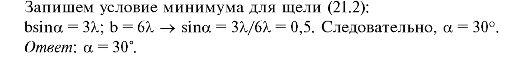2. Определить период решетки шириной L = 2,5 см, имеющей N = 12500 штрихов. Ответ записать в микрометрах.

Решение

d = L/N = 25 000 мкм/12 500 = 2 мкм. Ответ: d = 2 мкм.

3. Чему равна постоянная дифракционной решетки, если в спектре 2-го порядка красная линия (700 нм) видна под углом 30°?

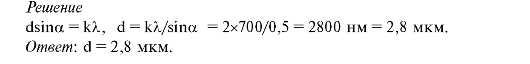4. Дифракционная решетка содержит N = 600 штрихов на L = 1 мм. Найти наибольший порядок спектра для света с длиной волны λ = 600 нм.

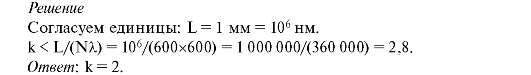5. Оранжевый свет с длиной волны 600 нм и зеленый свет с длиной волны 540 нм проходят через дифракционную решетку, имеющую 4000 штрихов на сантиметр. Чему равно угловое расстояние между оранжевым и зеленым максимумами: а) первого порядка; б) третьего порядка?

Δα = α_ор - α_з = 13,88° - 12,47° = 1,41°.

6. Найти наибольший порядок спектра для желтой линии натрия λ = 589 нм, если постоянная решетки равна d = 2 мкм.

Решение

Приведем d и λ к одинаковым единицам: d = 2 мкм = 2000 нм. По формуле (21.6) найдем k < d/λ = 2000/ 589 = 3,4. Ответ: k = 3.

7. Дифракционную решетку с числом щелей N = 10 000 используют для исследования спектра света в области 600 нм. Найти минимальную разность длин волн, которую можно обнаружить такой решеткой при наблюдении максимумов второго порядка.

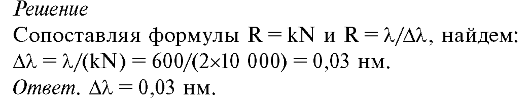8. Дифракционную решетку шириной L = 2 см с числом щелей N = 10 000 используют для исследования спектра света в области 600 нм. Найти минимальную разность длин волн, которую можно обнаружить такой решеткой.

Решение

Эта задача отличается от предыдущей тем, что не указан порядок максимума. Минимальная величина Δλ получается при максимально возможном значении k. По формуле (21.6) найдем