Медицинская и биологическая физика. Курс лекций с задачами : учеб. пособие / В.Н. Федорова, Е.В. Фаустов. - 2008. - 592 с.
|
|
|
|
ЛЕКЦИЯ 15 ПЕРЕМЕННЫЙ ТОК
1. Переменный ток и переменное напряжение. Сопротивление участка цепи при протекании переменного тока.
2. Протекание переменного тока по резистору. Сопротивление резистора, действующие значения тока и напряжения.
3. Конденсатор в цепи переменного тока, емкостное сопротивление.
4. Протекание переменного тока по идеальной катушке индуктивности, индуктивное сопротивление.
5. Протекание переменного тока по RLC-цепочке, импеданс. Резонанс напряжений. RCR-цепочка.
6. Импеданс тканей организма. Эквивалентная электрическая схема тканей. Реография.
7. Основные понятия и формулы.
8. Задачи.
15.1. Переменный ток и переменное напряжение. Сопротивление участка цепи при протекании переменного тока
В широком смысле «переменным» называют любой ток, который изменяется с течением времени по величине и направлению. В технике переменным называют ток, который изменяется со временем по гармоническому закону. Такой ток мы и будем рассматривать:
 Переменный
ток представляет собой вынужденные электромагнитные колебания, которые
возникают при подключении какоголибо прибора к сети переменного
напряжения:
Переменный
ток представляет собой вынужденные электромагнитные колебания, которые
возникают при подключении какоголибо прибора к сети переменного
напряжения:
 Обычно
начало отсчета времени выбирают так, чтобы для напряжения электрической
сети начальная фаза была равна нулю. Поэтому в формуле (15.2) нет
слагаемого φ0.
Обычно
начало отсчета времени выбирают так, чтобы для напряжения электрической
сети начальная фаза была равна нулю. Поэтому в формуле (15.2) нет
слагаемого φ0.
В цепи постоянного тока отношение напряжения к силе тока называется сопротивлением участка цепи (R = U/I). Аналогично вводят понятие сопротивления и для цепи переменного тока. Его величина обозначается буквой Х.
Сопротивление участка цепи в сети переменного тока равно отношению амплитудного значения переменного напряжения на этом участке к амплитудному значению силы тока в нем:
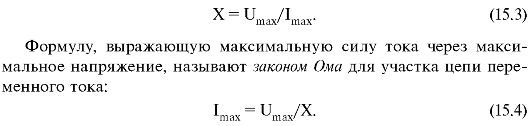 Максимальное значение переменного тока (Imax) и его начальная фаза (φ0)
зависят от свойств элементов, входящих в электрическую схему прибора.
Рассмотрим протекание переменного тока по таким элементам.
Максимальное значение переменного тока (Imax) и его начальная фаза (φ0)
зависят от свойств элементов, входящих в электрическую схему прибора.
Рассмотрим протекание переменного тока по таким элементам.
15.2. Протекание переменного тока по резистору. Сопротивление резистора, действующие значения тока и напряжения
Резистором называется проводник, не обладающий индуктивностью и емкостью.
Для всех частот переменного тока, который используется в технике, сопротивление резистора (XR) остается постоянным и совпадает с его сопротивлением в цепи постоянного тока:
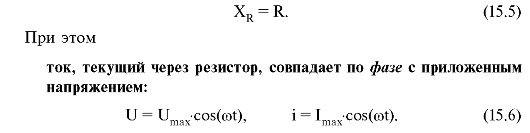 Резистор
- единственный элемент, для которого ток и напряжение совпадают по
фазе. Для того чтобы показать разность фаз между током и напряжением в
общем случае, используют векторную диаграмму, на которой вектор,
изображающий амплитудное напряжение (Umax), расположен под углом к оси токов. Угол, который вектор Umax образует с осью токов, показывает, насколько фаза напряжения опережает фазу тока.
Резистор
- единственный элемент, для которого ток и напряжение совпадают по
фазе. Для того чтобы показать разность фаз между током и напряжением в
общем случае, используют векторную диаграмму, на которой вектор,
изображающий амплитудное напряжение (Umax), расположен под углом к оси токов. Угол, который вектор Umax образует с осью токов, показывает, насколько фаза напряжения опережает фазу тока.
Цепь с резистором R и соответствующая ей векторная диаграмма представлены на рис. 15.1.
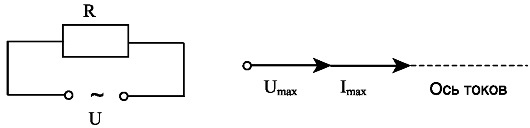 Рис. 15.1. Цепь переменного тока с резистором и ее векторная диаграмма
Рис. 15.1. Цепь переменного тока с резистором и ее векторная диаграмма
Поскольку ток и напряжение изменяются в одинаковой фазе, векторы Umax и Imax отложены по одной прямой в одном направлении.
В принципе любому переменному току сопутствует электромагнитное излучение. Однако для частот переменного тока, используемых в промышленности, интенсивность такого излучения ничтожно мала, и потерями энергии на электромагнитное излучение пренебрегают. Поэтому работа переменного тока, протекающего через резистор, полностью превращается в его внутреннюю энергию. В связи с этим сопротивление резистора называют активным.
Расчеты показывают, что средняя мощность, выделяемая в резисторе при протекании переменного (гармонического) тока, вычисляется по формулам
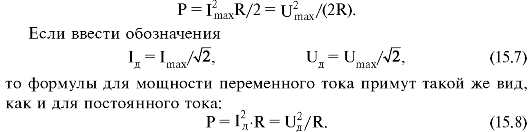 Значения переменного тока и напряжения, определяемые формулой (15.7), называются действующими. Существует договоренность
Значения переменного тока и напряжения, определяемые формулой (15.7), называются действующими. Существует договоренность
о том, что по умолчанию для цепи переменного тока указывают именно действующие значения. Например, напряжение в бытовой сети переменного тока равно 220 В. Указанное значение 220 В является действующим значением напряжения.
15.3. Конденсатор в цепи переменного тока,
емкостное сопротивление
Включим в цепь переменного напряжения (15.2) конденсатор емкостью С. Вместе с изменением напряжения будет меняться и заряд конденсатора, а в подводящих проводах возникнет ток. Заряд конденсатора связан с напряжением в цепи соотношением (см. формулу 10.16)
 Сопротивление конденсатора в цепи переменного тока называют емкостным сопротивлением. Его величину найдем по формулам (15.3, 15.9):
Сопротивление конденсатора в цепи переменного тока называют емкостным сопротивлением. Его величину найдем по формулам (15.3, 15.9):
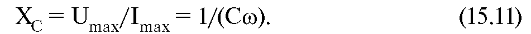 Цепь с конденсатором и соответствующая ей векторная диаграмма представлены на рис. 15.2.
Цепь с конденсатором и соответствующая ей векторная диаграмма представлены на рис. 15.2.
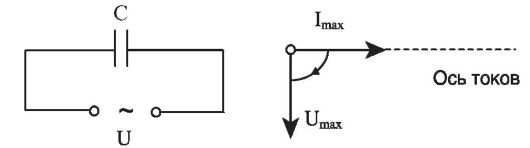 Рис. 15.2. Цепь переменного тока с конденсатором и ее векторная диаграмма
Рис. 15.2. Цепь переменного тока с конденсатором и ее векторная диаграмма
Поскольку напряжение отстает по фазе от тока на π/2, вектор Umax повернут относительно оси токов по часовой стрелке (в математике это направление считают отрицательным).
15.4. Протекание переменного тока по идеальной катушке индуктивности, индуктивное сопротивление
Включим в цепь переменного напряжения (15.2) катушку с индуктивностью L, активным сопротивлением которой можно пренебречь. Такую катушку называют идеальной. Вследствие самоиндукции в ней возникнет э.д.с., препятствующая изменению тока в цепи.
Поскольку активным сопротивлением катушки мы пренебрегаем, э.д.с. и напряжение одинаковы: ε = U. Используя формулу (10.15) для э.д.с. самоиндукции, получим дифференциальное уравнение для тока
 Цепь с катушкой L и соответствующая ей векторная диаграмма представлены на рис. 15.3.
Цепь с катушкой L и соответствующая ей векторная диаграмма представлены на рис. 15.3.
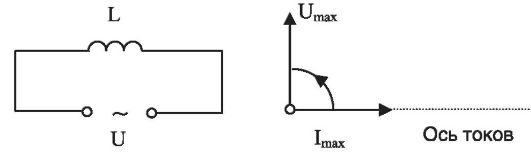 Рис. 15.3. Цепь переменного тока с катушкой и ее векторная диаграмма
Рис. 15.3. Цепь переменного тока с катушкой и ее векторная диаграмма
Поскольку напряжение опережает по фазе ток на π/2, то вектор Umax повернут относительно оси токов против часовой стрелки (в математике это направление считают положительным).
При протекании переменного тока по конденсатору и идеальной катушке индуктивности не происходит потерь энергии. Эти элементы половину периода забирают энергию из сети и преобразуют ее в энергию электрического и магнитного поля соответственно. Вторую половину периода энергия поля возвращается в сеть, поддерживая ток. В связи с отсутствием потерь энергии емкостное и индуктивное сопротивления называют реактивными.
15.5. Протекание переменного тока по RLC-цепочке, импеданс. Резонанс напряжений
Рассмотрим цепь, состоящую из последовательно соединенных резистора R, катушки индуктивности L и конденсатора С (рис. 15.4). Если на нее подать переменное напряжение (15.2), то ток в цепи будет отставать по фазе от напряжения на некоторый угол φ:
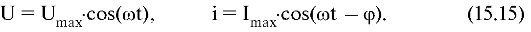 Такая цепь имеет как активное, так и реактивное сопротивления. Поэтому ее сопротивление называют импедансом и обозначают Z.
Такая цепь имеет как активное, так и реактивное сопротивления. Поэтому ее сопротивление называют импедансом и обозначают Z.
Импеданс равен отношению амплитудного значения переменного напряжения на концах цепи к амплитудному значению силы тока в ней:
Z = Umax/Imax.
 Рис. 15.4. RLC-цепь в сети переменного тока и соответствующая ей векторная диаграмма
Рис. 15.4. RLC-цепь в сети переменного тока и соответствующая ей векторная диаграмма
RLC-цепь и соответствующая ей векторная диаграмма представлены на рис. 15.4.
Элементы RLC-цепочки соединены последовательно. Поэтому по ним протекает одинаковый ток, а приложенное напряжение U(t) складывается из напряжений на отдельных участках цепи:
 Резонанс напряжений
Резонанс напряжений
Если величины L, C и ω подобраны таким образом, что Xc = Xl, то импеданс Z (формула 15.16) имеет минимально возможное значение, равное R (Z = R). При этом амплитуда тока максимальна, а приложенное напряжение и ток изменяются в одной фазе (φ = 0). Данное
явление называется резонансом напряжений. Подставив в условие резонанса (XC = XL) выражения (15.11), (15.14), получим формулу для расчета резонансной частоты:
 RCR- цепочка
RCR- цепочка
Рассмотрим протекание тока по параллельной RCR-цепочке, которая моделирует проводящие свойства биологической ткани (рис. 15.5). Если ее включить в сеть переменного напряжения (15.2), то по нижнему и верхнему участкам будут протекать токи:
 Вектор его амплитуды I равен сумме амплитуд I1 и I2, а угол опережения φ показан на рис. 15.5,б.
Вектор его амплитуды I равен сумме амплитуд I1 и I2, а угол опережения φ показан на рис. 15.5,б.
Приведем без вывода формулу для нахождения импеданса RCR- цепочки:
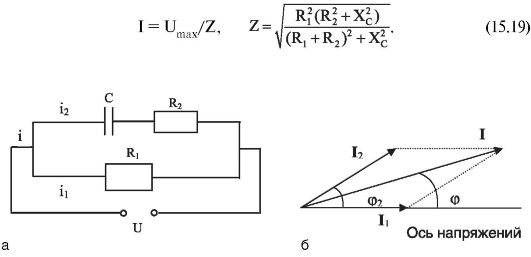 Рис. 15.5. RCR-цепочка и ее векторная диаграмма
Рис. 15.5. RCR-цепочка и ее векторная диаграмма
15.6. Импеданс тканей организма. Эквивалентная электрическая схема тканей. Дисперсия импеданса. Реография
Импеданс тканей организма
Электрические свойства тканей организма различны. Органические вещества (белки, жиры, углеводы) являются диэлектриками. В состав тканевых жидкостей входят электролиты.
Ткани состоят из клеток, важной частью которых являются мембраны. Двойной фосфолипидный слой уподобляет мембрану конденсатору.
В организме нет таких систем, которые были бы подобны катушкам индуктивности, поэтому индуктивность его близка к нулю.
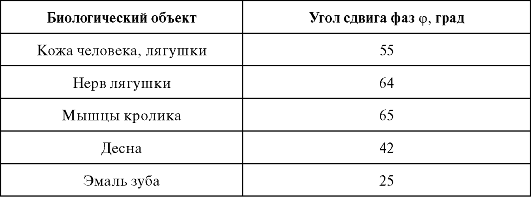
Таким образом, импеданс тканей определяется только активным и емкостным сопротивлениями. Наличие в биологических системах емкостных элементов подтверждается тем, что сила тока опережает по фазе приложенное напряжение. Величина угла опережения для разных биологических объектов при частоте 1 кГц приводится в таблице.
 Эквивалентная электрическая схема тканей
Эквивалентная электрическая схема тканей
В общем случае органическую ткань можно рассматривать как клетки, находящиеся в проводящей среде (R1), роль которой играет, например, межклеточная жидкость (рис. 15.6). Клеточные мембраны обладают емкостными свойствами, а электролиты внутри клетки обладают активным сопротивлением (R2).
Этому представлению соответствует электрическая схема, рассмотренная в разделе 15.5 (см. рис. 15.5). На рисунке 15.7 показана зависимость импеданса от круговой частоты тока, которая получается из формулы (15.19) после подстановки в нее выражения для
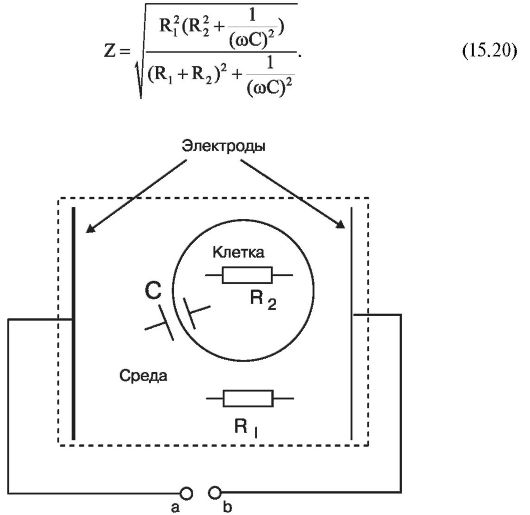 Рис. 15.6. Электрические свойства биологических тканей
Рис. 15.6. Электрические свойства биологических тканей
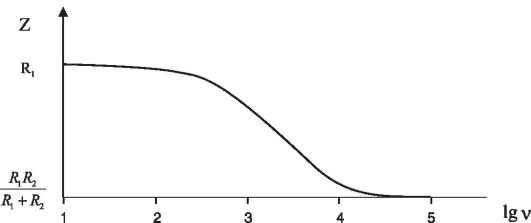 Рис. 15.7. Зависимость импеданса от частоты для RCR-цепочки
Рис. 15.7. Зависимость импеданса от частоты для RCR-цепочки
 Дисперсия импеданса
Дисперсия импеданса
Кривая на рис. 15.7 качественно верно описывает изменение импеданса биологической ткани: плавное уменьшение импеданса при росте частоты. Однако для реальных биологических тканей эта зависимость сложнее. На рисунке 15.8 представлен график частотной зависимости импеданса мышечной ткани, полученный экспериментально (масштаб на вертикальной оси - логарифмический).
На графике четко проявляются три интервала частот, в которых величина Z медленнее меняется с частотой по сравнению с общим ходом кривой. Они названы областями α-, β- и γ-дисперсии соответственно. Им соответствуют три области частот: низкие частоты ν < 10 кГц, радиочастоты ν = 0,1-10 МГц, микроволновые частоты ν > 0,1 ГГц.
Наличие областей α-, β- и γ-дисперсии связано с частотной дисперсией диэлектрической проницаемости (ε = f(v)), от которой зависит величина емкости (см. формулу 10.20). На рисунке 15.9 показаны структурные элементы, вносящие основной вклад в поляризацию ткани на различных частотах:
- α-дисперсия обусловлена поляризацией целых клеток (1, 2) в результате диффузии ионов, что требует относительно большого времени, поэтому данный механизм проявляется при действии электрического поля низкой частоты (0,1-10 кГц). В этой области емкостное сопротивление мембран велико и преобладают токи, протекающие через растворы электролитов, окружающие фрагменты мембран.
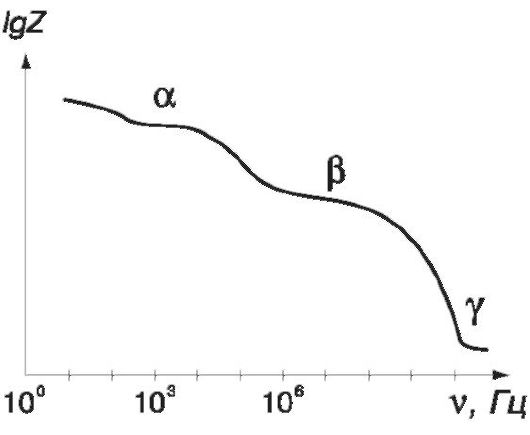 Рис. 15.8. Частотная зависимость импеданса биологической ткани
Рис. 15.8. Частотная зависимость импеданса биологической ткани
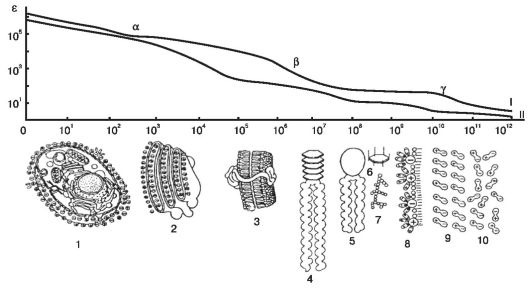 Рис. 15.9. Структурные элементы, вносящие основной вклад в поляризацию ткани
Рис. 15.9. Структурные элементы, вносящие основной вклад в поляризацию ткани
Поляризация клеток - самый медленный процесс среди всех механизмов поляризации. При увеличении частоты поляризация клеток практически полностью прекращается.
- β-дисперсия обусловлена структурной поляризацией клеточных мембран (3), в которой участвуют белковые макромолекулы (4), а на ее верхней границе - глобулярные водорастворимые белки (5), фосфолипиды (6, 7) и мельчайшие субклеточные структуры (8). При этом получаются существенно меньшие значения диэлектрической проницаемости, чем при поляризации целых клеток. Этот механизм поляризации доминирует на частотах 1-10 МГц. При дальнейшем увеличении частоты перестает работать и этот механизм.
- γ-дисперсия обусловлена процессами ориентационной поляризации молекул (9, 10) свободной и связанной воды, а также низкомолекулярных веществ типа сахаров и аминокислот. При этом диэлектрическая проницаемость уменьшается еще больше. Этот механизм поляризации доминирует на частотах выше 1 ГГц.
В частотных диапазонах, соответствующих главным областям дисперсии, происходят наибольшие потери энергии переменного электрического тока (поля). Выделение энергии происходит на том структурном уровне, который отвечает за данную область диспер-
сии. На этом основано действие различных методов физиотерапии с использованием переменных токов и полей.
Импеданс ткани зависит не только от частоты, но и от состояния ткани. Частотная зависимость импеданса позволяет оценить жизнеспособность тканей организма. Это используют при пересадке (трансплантации) тканей и органов. Так, например, определение жизнеспособности трансплантата является одной из первоочередных задач офтальмохирургии. Такая оценка нужна и при определении тактики лечения ожогов роговицы, при кератопластике и кератопротезировании на глазах с бельмом (помутнение роговицы глаза), при наблюдении за течением кератита (воспаление роговицы), для определения пригодности консервативного донорского материала.
Реография
Импеданс тканей и органов зависит от их физиологического состояния и от степени наполнения кровеносных сосудов, проходящих в этих тканях. При наполнении ткани кровью во время систолы полное сопротивление ткани уменьшается, а при диастоле увеличивается. Импеданс изменяется в такт с работой сердца. Это используется в диагностических целях.
Реография - диагностический метод, основанный на регистрации изменения импеданса тканей в процессе сердечной деятельности.
Эти изменения представляются в виде реограммы. Пример реограммы голени здорового человека представлен на рис. 15.10.
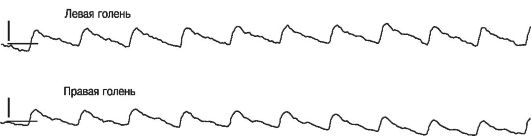 Рис. 15.10. Реограмма голени здорового человека
Рис. 15.10. Реограмма голени здорового человека
При наполнении сосудов кровью величина электропроводимости тканей изменяется, а вместе с ней изменяется и величина импеданса.
По скорости изменения полного сопротивления можно судить о быстроте притока крови при систоле и оттока крови во время диастолы.
С помощью этого метода получают реограммы головного мозга (реоэнцефалограмма), сердца (реокардиограмма), магистральных сосудов, легких, печени, конечностей. Исследование реограмм применяют в диагностике заболеваний периферических кровеносных сосудов, сопровождающихся изменением их эластичности, сужением артерий и т.д.
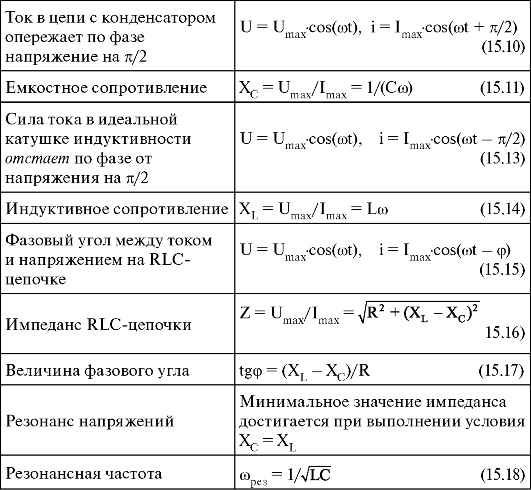
15.7. Основные понятия и формулы
 Окончание таблицы
Окончание таблицы
 15.8. Задачи
15.8. Задачи
1. Напряжение и сила тока в цепи изменяются по закону U = 60sin(314t + 0,25) мВ, i = 15sin(314t) мА. Определить импеданс цепи Z и фазовый угол между током и напряжением.
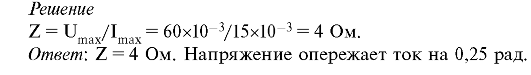 2. Допустимо ли в цепь переменного тока напряжением 220 В включать конденсатор, напряжение пробоя для которого равно 250 В?
2. Допустимо ли в цепь переменного тока напряжением 220 В включать конденсатор, напряжение пробоя для которого равно 250 В?
 5. Частота переменного тока равна 50 Гц. Сколько раз за секунду напряжение равно нулю?
5. Частота переменного тока равна 50 Гц. Сколько раз за секунду напряжение равно нулю?
Ответ: 100 раз.
6. Найти полное сопротивление переменному току, если последовательно включены:
а) резистор сопротивлением R1 = 3 Ом и катушка с индуктивным сопротивлением XL = 4 Ом;
б) резистор сопротивлением R2 = 6 Ом и конденсатор с емкостным сопротивлением XC = 8 Ом;
в) резистор сопротивлением R3 = 12 Ом, конденсатор емкостным сопротивлением XC = 8 Ом и катушка с индуктивным сопротивлением XL = 24 Ом.
Ответ: а) 5 Ом; б) 10 Ом; в) 20 Ом.
7. Сколько времени будет гореть неоновая лампочка, если ее на 1 минуту подключить в сеть переменного тока с действующим напряжением 120 В и частотой 50 Гц. Лампочка зажигается и гаснет при напряжении 84,5 В.
 График зависимости U(t) представлен на рис. 15.11.
График зависимости U(t) представлен на рис. 15.11.
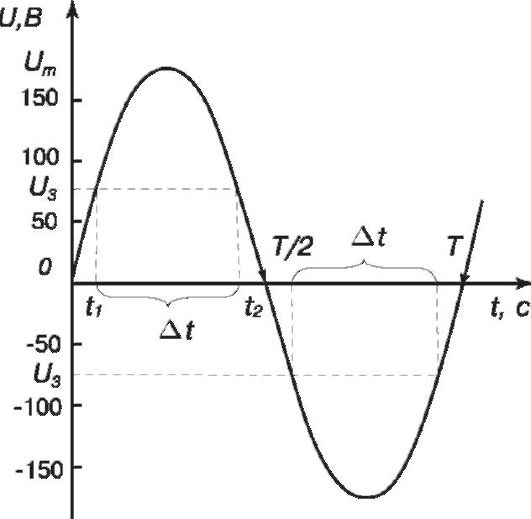 Рис. 15.11.
Рис. 15.11.
На графике обозначено напряжение зажигания лампы Uз и соответствующие ему два момента времени: t1 - время зажигания
лампы, когда мгновенные значения напряжения становятся больше Uз; t2 - время, когда лампочка гаснет, так как мгновенные значения напряжения становятся меньше напряжения Uз.Очевидно, что длительность одной вспышки
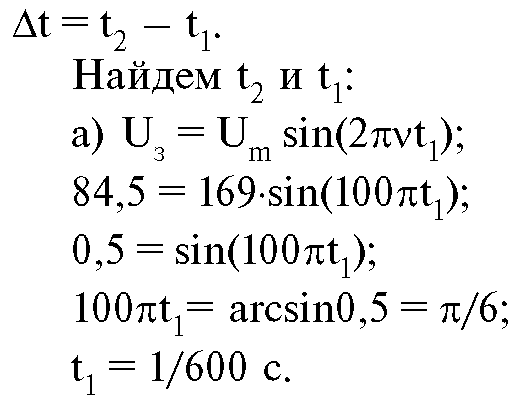
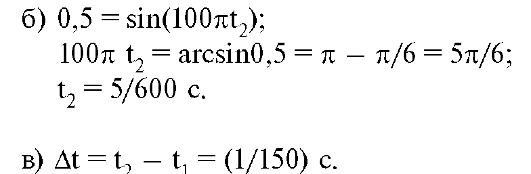 В
течение одного колебания напряжения лампочка загорается 2 раза, так как
работа неоновой лампы не зависит от полярности приложенного напряжения
(см. рис. 15.11). Поэтому число колебаний напряжения за время t0 равно (t0- ν), а число вспышек за это время h = 2t0 ? v.
В
течение одного колебания напряжения лампочка загорается 2 раза, так как
работа неоновой лампы не зависит от полярности приложенного напряжения
(см. рис. 15.11). Поэтому число колебаний напряжения за время t0 равно (t0- ν), а число вспышек за это время h = 2t0 ? v.
Тогда время, в течение которого светится лампа, равно
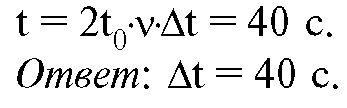 8. Неоновая
лампа включена в сеть переменного тока с действующим значением 71 В и
периодом 0,02 с. Напряжение зажигания лампы, равное 86,7 В, считать
равным напряжению гашения. Найти: а) значение промежутка времени, в
течение которого длится вспышка лампы; б) частоту вспышек.
8. Неоновая
лампа включена в сеть переменного тока с действующим значением 71 В и
периодом 0,02 с. Напряжение зажигания лампы, равное 86,7 В, считать
равным напряжению гашения. Найти: а) значение промежутка времени, в
течение которого длится вспышка лампы; б) частоту вспышек.
Ответ: а) 3,3 мс; б) 100 Гц.
9. Действующее напряжение в электросети 220 В. На какое напряжение должна быть рассчитана изоляция провода?
Решение