ЛЕКЦИЯ 13 ДИПОЛЬ. ФИЗИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОГРАФИИ

Электрический диполь - система из двух равных по величине, но противоположных по знаку точечных электрических зарядов, расположенных на некотором расстоянии друг от друга.

Расстояние между зарядами называется плечом диполя.

Основной характеристикой диполя является векторная величина, называемая электрическим моментом диполя (P).

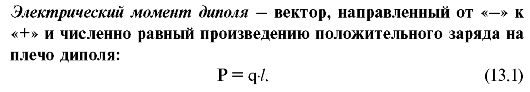Электрическое поле диполя

Диполь является источником электрического поля, силовые линии и эквипотенциальные поверхности которого изображены на рис. 13.1.

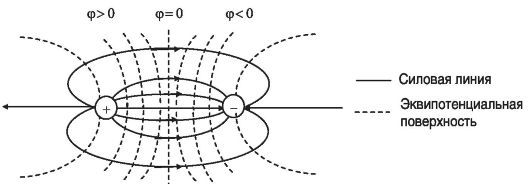Рис. 13.1. Диполь и его электрическое поле

Центральная эквипотенциальная поверхность представляет собой плоскость, проходящую перпендикулярно плечу диполя через его середину. Все ее точки имеют нулевой потенциал (φ = 0). Она делит электрическое поле диполя на две половины, точки которых имеют соответственно положительные (φ > 0) и отрицательные (φ < 0) потенциалы.

Абсолютная величина потенциала зависит от дипольного момента Р, диэлектрической проницаемости среды ε и от положения данной точки поля относительно диполя. Пусть диполь находится в непроводящей бесконечной среде и некоторая точка А удалена от его центра на расстояние r >> λ (рис. 13.2). Обозначим через α угол между вектором Р и направлением на эту точку. Тогда потенциал, создаваемый диполем в точке А, определяется следующей формулой:

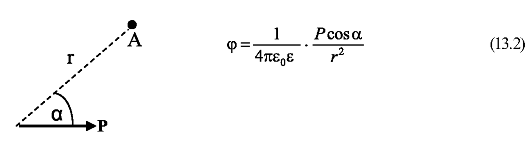Рис. 13.2. Потенциал электрического поля, созданного диполем

Диполь в равностороннем треугольнике

Если диполь поместить в центр равностороннего треугольника, то он будет равноудален ото всех его вершин (на рис. 13.3 диполь изображен вектором дипольного момента - Р).

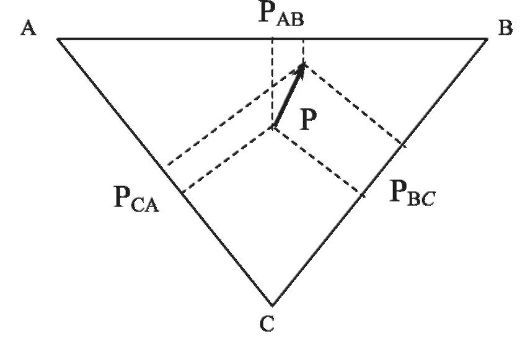Рис. 13.3. Диполь в равностороннем треугольнике

Можно показать, что в этом случае разность потенциалов (напряжение) между двумя любыми вершинами прямо пропорциональна проекции дипольного момента на соответствующую сторону (U_AB ~ P_AB). Поэтому отношение напряжений между вершинами треугольника равно отношению проекций дипольного момента на соответствующие стороны:

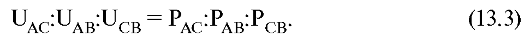Сопоставляя величины проекций, можно судить о величине самого вектора и его расположении внутри треугольника.

13.2. Диполь во внешнем электрическом поле

Диполь не только сам является источником электрического поля, но и взаимодействует с внешним электрическим полем, созданным другими источниками.

Диполь в однородном электрическом поле

В однородном электрическом поле напряженностью E на полюса диполя действуют равные по величине и противоположные по направлению силы (рис. 13.4). Поскольку сумма таких сил равна нулю, поступательного движения они не вызывают. Однако они

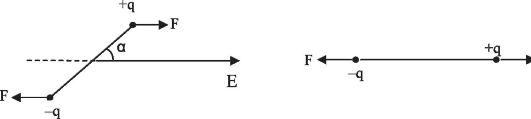Рис. 13.4. Диполь в однородном электрическом поле

создают вращательный момент, величина которого определяется следующей формулой:

Этот момент «стремится» расположить диполь параллельно линиям поля, т.е. перевести его из некоторого положения (а) в положение (б).

Диполь в неоднородном электрическом поле

В неоднородном электрическом поле величины сил, действующих на полюсы диполя (силы F⁺ и F^- на рис. 13.5), неодинаковы, и их сумма не равна нулю Поэтому возникает равнодействующая сила, втягивающая диполь в область более сильного поля.

Величина втягивающей силы, действующей на диполь, ориентированный вдоль силовой линии, зависит от градиента напряженности и вычисляется по формуле:

Здесь ось Х - направление силовой линии в том месте, где находится диполь.

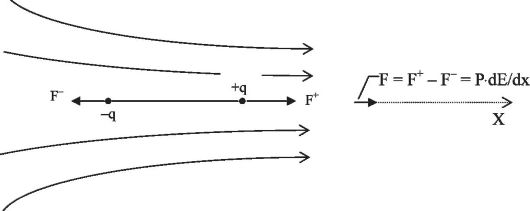Рис. 13.5. Диполь в неоднородном электрическом поле. Р - дипольный момент

13.3. Токовый диполь

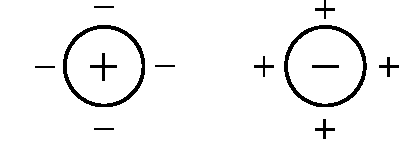Рис. 13.6. Экранирование диполя в проводящей среде

В непроводящей среде электрический диполь может сохраняться сколь угодно долго. Но в проводящей среде под действием электрического поля диполя возникает смещение свободных зарядов, диполь экранируется и перестает существовать (рис. 13.6).

Для сохранения диполя в проводящей среде необходима электродвижущая сила. Пусть в проводящую среду (например, в сосуд с раствором электролита) введены два электрода, подключенные к источнику постоянного напряжения. Тогда на электродах будут поддерживаться постоянные заряды противоположных знаков, а в среде между электродами возникнет электрический ток. Положительный электрод называют истоком тока, а отрицательный - стоком тока.

Двухполюсная система в проводящей среде, состоящая из истока и стока тока, называется дипольным электрическим генератором или токовым диполем.

Расстояние между истоком и стоком тока (L) называется плечом токового диполя.

На рис. 13.7,а сплошными линиями со стрелками изображены линии тока, создаваемого дипольным электрическим генерато-

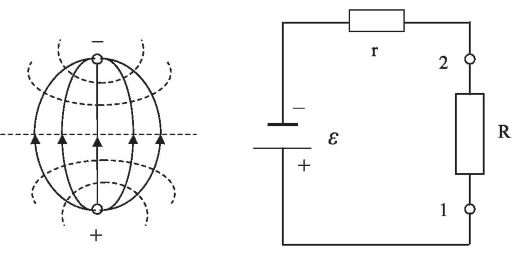Рис. 13.7. Токовый диполь и его эквивалентная электрическая схема

ром, а пунктирными линиями - эквипотенциальные поверхности. Рядом (рис. 13.7, б) показана эквивалентная электрическая схема: R - сопротивление проводящей среды, в которой находятся электроды; r - внутреннее сопротивление источника, ε - его э.д.с.; положительный электрод (1) - исток тока; отрицательный электрод (2) - сток тока.

Обозначим сопротивление среды между электродами через R. Тогда сила тока определяется законом Ома:

Если сопротивление среды между электродами значительно меньше, чем внутреннее сопротивление источника, то I = ε/r.

Для того чтобы сделать картину более наглядной, представим себе, что в сосуд с электролитом опущены не два электрода, а обычный элемент питания. Линии электрического тока, возникшего в сосуде в этом случае, показаны на рис. 13.8.

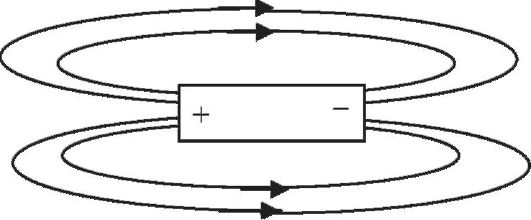Рис. 13.8. Токовый диполь и созданные им линии тока

Электрической характеристикой токового диполя является векторная величина, называемая дипольным моментом (Р_T).

Дипольный момент токового диполя - вектор, направленный от стока (-) к истоку (+) и численно равный произведению силы тока на плечо диполя:

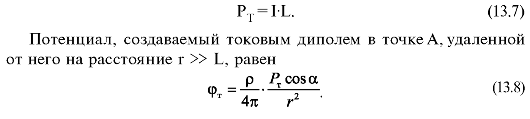Здесь ρ - удельное сопротивление среды. Геометрические характеристики такие же, как на рис. 13.2.

Таким образом, между токовым диполем и электрическим диполем существует полная аналогия.

Теория токового диполя применяется для модельного объяснения возникновения потенциалов, регистрируемых при снятии электрокардиограмм.

13.4. Физические основы электрографии

Живые ткани являются источником электрических потенциалов. Регистрация биопотенциалов тканей и органов называется электрографией.

В медицинской практике используют следующие диагностические методы:

• ЭКГ - электрокардиография - регистрация биопотенциалов, возникающих в сердечной мышце при ее возбуждении;

• ЭРГ - электроретинография - регистрация биопотенциалов сетчатки глаза, возникающих в результате воздействия на глаз;

• ЭЭГ - электроэнцефалография - регистрация биоэлектрической активности головного мозга;

• ЭМГ - электромиография - регистрация биоэлектрической активности мышц.

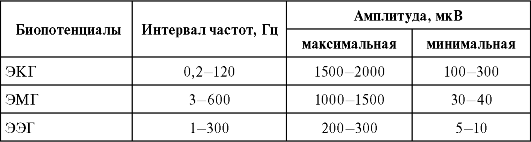
Примерная характеристика регистрируемых при этом биопотенциалов указана в табл. 13.1.

Таблица 13.1 Характеристики биопотенциалов

При изучении электрограмм решаются две задачи: 1) прямая - выяснение механизма возникновения электрограммы или расчет потенциала в области измерения по заданным характеристикам электрической модели органа;

2) обратная (диагностическая) - выявление состояния органа по характеру его электрограммы.

Почти во всех существующих моделях электрическую активность органов и тканей сводят к действию определенной совокупности токовых электрических генераторов, находящихся в объемной электропроводящей среде. Для токовых генераторов выполняется правило суперпозиции электрических полей:

Потенциал поля генераторов равен алгебраической сумме потенциалов полей, создаваемых генераторами.

Дальнейшее рассмотрение физических вопросов электрографии показано на примере электрокардиографии.

13.5. Теория отведений Эйнтховена, три стандартных отведения. Поле диполя сердца, анализ электрокардиограмм

Сердце человека - мощная мышца. При синхронном возбуждении множества волокон сердечной мышцы в среде, окружающей сердце, течет ток, который даже на поверхности тела создает разности потенциалов порядка нескольких мВ. Эта разность потенциалов регистрируется при записи электрокардиограммы.

Моделировать электрическую активность сердца можно с использованием дипольного эквивалентного электрического генератора.

Дипольное представление о сердце лежит в основе теории отведений Эйнтховена, согласно которой:

сердце есть токовый диполь с дипольным моментом Р_с, который поворачивается, изменяет свое положение и точку приложения за время сердечного цикла.

(В биологической литературе вместо термина «дипольный момент сердца» обычно используются термины «вектор электродвижущей силы сердца», «электрический вектор сердца».)

По Эйнтховену, сердце располагается в центре равностороннего треугольника, вершинами которого являются: правая рука - левая рука - левая нога. (Вершины треугольника равноудалены как друг

от друга, так и от центра треугольника.) Поэтому разности потенциалов, снятые между этими точками, суть проекции дипольного момента сердца на стороны этого треугольника. Пары точек, между которыми измеряются разности биопотенциалов, со времен Эйнтховена в физиологии принято называть «отведениями».

Таким образом, теория Эйнтховена устанавливает связь между разностью биопотенциалов сердца и разностями потенциалов, регистрируемых в соответствующих отведениях.

Три стандартных отведения

На рисунке 13.9 представлены три стандартных отведения.

Отведение I (правая рука - левая рука), отведение II (правая рука - левая нога), отведение III (левая рука - левая нога). Им соответствуют разности потенциалов U_I, U_II, U_lII. Направление вектора Р_с определяет электрическую ось сердца. Линия электрической оси сердца при пересечении с направлением I-го отведения образует угол α. Величина этого угла определяет направление электрической оси сердца.

Соотношения между разностью потенциалов на сторонах треугольника (отведениях) могут быть получены в соответствии с формулой (13.3) как соотношения проекций вектора Р_с на стороны треугольника:

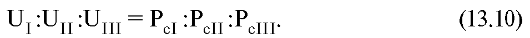Так как электрический момент диполя - сердца - изменяется со временем, то в отведениях будут получены временные зависимости напряжения, которые и называют электрокардиограммами.

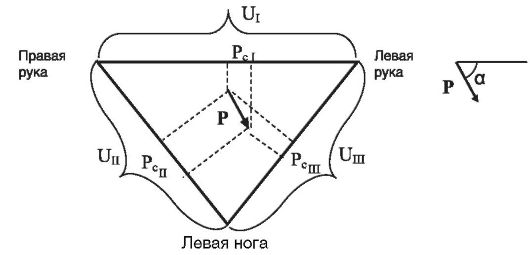Рис. 13.9. Схематическое изображение трех стандартных отведений ЭКГ

Допущения теории Эйнтховена

Электрическое поле сердца на больших расстояниях от него подобно полю токового диполя; дипольный момент - интегральный электрический вектор сердца (суммарный электрический вектор возбужденных в данный момент клеток).

Все ткани и органы, весь организм - однородная проводящая среда (с одинаковым удельным сопротивлением).

Электрический вектор сердца изменяется по величине и направлению за время сердечного цикла, однако начало вектора остается неподвижным.

Точки стандартных отведений образуют равносторонний треугольник (треугольник Эйнтховена), в центре которого находится сердце - токовый диполь. Проекции дипольного момента сердца - отведения Эйнтховена.

Поле диполя - сердца

В каждый данный момент деятельности сердца его дипольный электрический генератор создает вокруг электрическое поле, которое распространяется по проводящим тканям тела и создает потенциалы в его различных точках. Если представить, что основание сердца заряжено отрицательно (имеет отрицательный потенциал), а верхушка положительно, то распределение эквипотенциальных линий вокруг сердца (и силовых линий поля) при максимальном значении дипольного момента Р_с будет таким, как на рис. 13.10.

Потенциалы указаны в некоторых относительных единицах. Вследствие асимметричного положения сердца в грудной клетке его электрическое поле распространяется преимущественно в сторону правой руки и левой ноги, и наиболее высокая разность потенциалов может быть зафиксирована в том случае, если электроды разместить на правой руке и левой ноге.

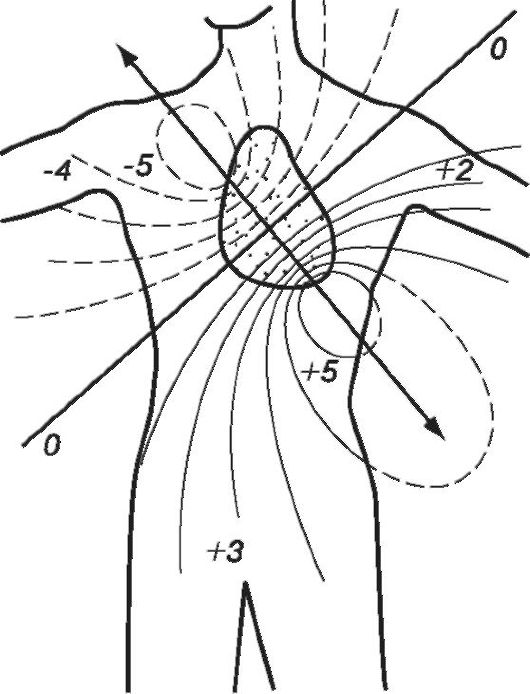Рис. 13.10. Распределение силовых (сплошные) и эквипотенциальных (прерывистые) линий на поверхности тела

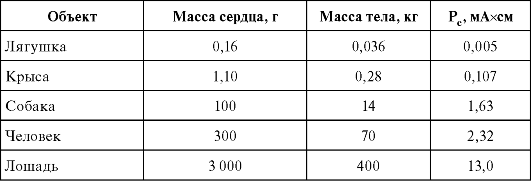
В таблице 13.2 приведены значения максимального дипольного момента сердца в сопоставлении с массой сердца и тела.

Таблица 13.2. Значения дипольного момента Р_с

Анализ электрокардиограмм

Теоретический анализ электрокардиограмм сложен. Развитие кардиографии шло в основном эмпирическим путем. Катц указывал, что расшифровка электрокардиограмм производится на основе опыта, опирающегося лишь на самое элементарное понимание теории возникновения биопотенциалов.

Данные ЭКГ обычно дополняют клиническую картину заболевания.

На рисунке 13.11 представлена нормальная электрокардиограмма человека (обозначения зубцов были даны Эйнтховеном и представляют взятые подряд буквы латинского алфавита).

Она представляет собой график изменения во времени разности потенциалов, снимаемой двумя электродами соответствующего отведения за цикл работы сердца. Горизонтальная ось является не только осью времени, но и осью нулевого потенциала. ЭКГ представляет собой кривую, состоящую из трех характерных зубцов, обозначающихся Р, QRS, T, разделенных интервалом нулевого потенциала. Высоты зубцов в различных отведениях обусловлены направлением электрической оси сердца, т.е. углом α (см. рис. 13.9). Электрокардиограмма, записанная при норме в стандартных отведениях, характеризуется тем, что ее зубцы в разных отведениях будут неодинаковы по амплитуде (рис. 13.12).

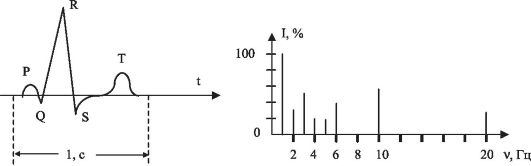Рис. 13.11. Электрокардиограмма здорового человека и ее спектр:

Р - деполяризация предсердия; QRS -деполяризация желудочков; Т - репо-

ляризация; частота пульса 60 ударов в минуту (период сокращения - 1 с)

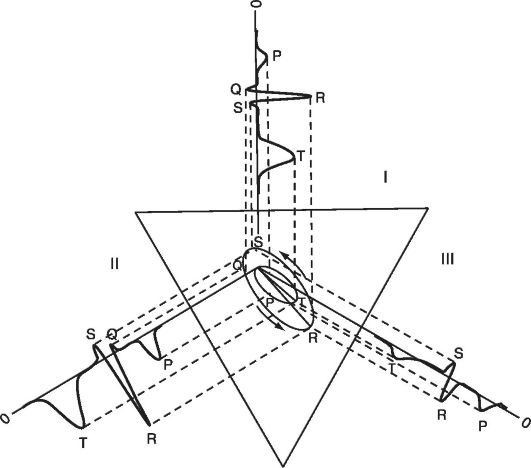Рис. 13.12. Нормальная ЭКГ в трех стандартных отведениях

Зубцы ЭКГ будут наиболее высокими во II отведении и наиболее низкими в III отведении (при нормальном положении электрической оси).

Сопоставляя кривые, зарегистрированные в трех отведениях, можно судить о характере изменения Р_с за цикл работы сердца, на основании чего и составляется представление о состоянии нервномышечного аппарата сердца.

Для анализа ЭКГ используют также ее гармонический спектр.

13.6. Векторкардиография

Обычные электрокардиограммы являются одномерными. В 1957 г. немецкий врач физиолог Шмитт разработал метод объемных кривых (векторкардиография).

Напряжение от двух взаимно перпендикулярных отведений подают на взаимно перпендикулярные пластины осциллографа. При этом на экране получается изображение, состоящее из двух петель - большой и малой. Малая петля заключена в большой и сдвинута к одному из полюсов.

Вторая аналогичная картина может быть получена на втором осциллографе, где одно из двух уже использованных отведений сопоставляется с третьим. Картины на обоих осциллографах можно рассматривать через стереоскопическую систему линз или фотографировать одновременно, чтобы в дальнейшем построить пространственную (трехмерную) модель.

Для расшифровки электрокардиограмм нужен большой опыт. С появлением ЭВМ стало возможным автоматизировать процесс «чтения» кривых. ЭВМ сравнивает кривую данного больного с образцами, хранящимися в ее памяти, и выдает врачу предположительный диагноз.

Иной подход используется при проведении электрокардиотопографического исследования. При этом на грудную клетку накладывают около 200 электродов, строят картину электрического поля по 200 кривым, которые анализируются одновременно.

13.7. Физические факторы, определяющие особенности ЭКГ

ЭКГ у разных людей и даже у одного и того же человека характеризуются большой вариабельностью. Это связано с индивидуальными анатомическими особенностями проводниковой системы сердца, различиями в соотношении мышечных масс анатомических фрагментов сердца, электропроводностью окружающих сердце тканей, индивидуальной реакцией нервной системы на воздействие внешних и внутренних факторов.

Факторы, определяющие особенности ЭКГ у отдельного человека, следующие: 1) положение сердца в грудной клетке, 2) положение тела, 3) дыхание, 4) действие физических раздражителей, в первую очередь физических нагрузок.

Положение сердца в грудной клетке оказывает существенное влияние на форму ЭКГ. При этом надо знать, что направление электрической оси сердца совпадает с анатомической осью сердца. Если угол α, характеризующий направление электрической оси сердца (рис. 13.9), имеет величину:

а) в пределах от 40 до 70°, то такое положение электрической оси сердца считается нормальным; в этих случаях ЭКГ будет иметь обычные соотношения зубцов в I, II, III стандартных отведениях;

б) близкую к 0°, т.е. электрическая ось сердца параллельна линии первого отведения, то такое положение электрической оси сердца обозначается как горизонтальное, и ЭКГ характеризуется высокими амплитудами зубцов в I отведении;

в) близкую к 90°, положение обозначается как вертикальное, зубцы ЭКГ будут наименьшими в I отведении.

Как правило, положение анатомической и электрической осей сердца совпадают. Но в отдельных случаях может быть расхождение: рентгенограмма свидетельствует о нормальном положении сердца, а ЭКГ показывает отклонение электрической оси в ту или другую сторону. Такие расхождения являются диагностически значимыми (клинически это означает одностороннее поражение миокарда).

Изменение положения тела всегда вызывает некоторые изменения положения сердца в грудной клетке. Это сопровождается изменением

электропроводности окружающих сердце сред. ЭКГ у человека с вертикальным положением сердца будет отличаться от нормальной. Если ЭКГ не изменяет своей формы при перемещении тела, то этот факт тоже имеет диагностическое значение; характеристики зубцов изменяются при любом отклонении электрической оси.

Дыхание. Амплитуда и направленность зубцов ЭКГ изменяются при любом отклонении электрической оси, меняясь при вдохе и выдохе. При вдохе электрическая ось сердца отклоняется примерно на 15°, при глубоком вдохе это отклонение может достичь 30°. Нарушения или изменения дыхания (при тренировках, при реабилитационных упражнениях и гимнастике) могут быть диагностированы по изменению ЭКГ.

Физическая нагрузка. В медицине роль физических нагрузок чрезвычайно велика. Физическая нагрузка всегда вызывает существенное изменение в ЭКГ. У здоровых людей эти изменения состоят, главным образом, в учащении ритма, форма зубцов тоже изменяется в определенной закономерности. При функциональных пробах с физической нагрузкой могут иметь место такие изменения, которые явно указывают на патологические изменения в работе сердца (тахикардия, экстрасистолия, мерцательная аритмия и т.д.).

Искажения при записи ЭКГ. При записи ЭКГ всегда нужно иметь в виду, что существуют причины, которые могут исказить ее форму: неисправности в усилителе электрокардиографа; переменный ток городской сети может наводить э.д.с. вследствие электромагнитной индукции в рядом расположенных усилительных цепях и даже биологических объектах, нестабильность блока питания и т.д. Расшифровка искаженной ЭКГ приводит к постановке неправильного диагноза.

Диагностическая значимость метода электрокардиографии, несомненно, велика. Совместно с другими методами оценки деятельности сердца (методы регистрации механических колебаний сердца, рентгеновский метод) он позволяет получать важную клиническую информацию о работе сердца.

В последние годы в современной врачебно-диагностической практике стали использоваться компьютерные электрокардиографы со средствами автоматического анализа ЭКГ.

13.8. Основные понятия и формулы

Окончание таблицы