ЛЕКЦИЯ 11 ФИЗИЧЕСКИЕ ПРОЦЕССЫ В МЕМБРАНАХ

1. Функции мембран.

2. Структура и модели мембран.

3. Физические свойства мембран.

4. Перенос молекул (атомов) через мембраны, уравнение Фика.

5. Перенос заряженных частиц, электродиффузное уравнение Нернста-Планка.

6. Виды транспорта через мембраны: пассивный и активный.

7. Основные понятия и формулы.

8. Задачи.

Изучение структуры и функционирования биологических мембран играет важную роль в медицине, так как многие патологические процессы в клетке связаны с нарушением функций мембран. Общая площадь мембран в органах и тканях достигает огромных размеров. Благодаря этому клетки располагают достаточной площадью для протекания на мембранах многочисленных процессов, обеспечивающих жизнеспособность человека.

11.1. Функции мембран

Мембрана выполняет в жизнедеятельности живых клеток (рис. 11.1) самые различные функции.

Механическое разделение. Клетка - элементарная живая система. Каждая клетка окружена наружной клеточной плазматической мембраной, которая заключает внутри себя содержимое клетки. С другой стороны, тонкая регуляция внутриклеточных процессов осуществляется на основе пространственного разделения органоидов клетки (внутриклеточные мембраны). Мембрана является поверхностью раздела (диэлектрической границей).

Транспортная функция. Через мембрану происходит перенос (транспорт) различных веществ, т.е. она принимает активное участие в жизнедеятельности клетки.

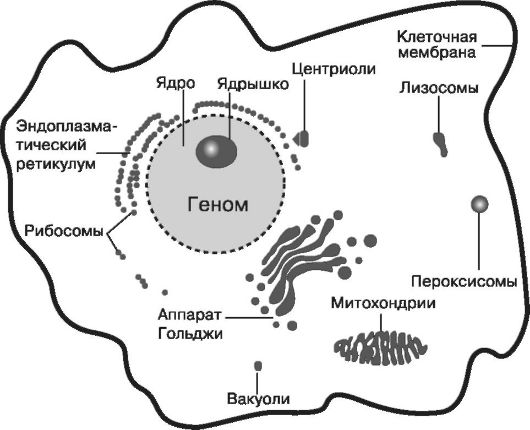Рис. 11.1. Схема строения клетки

Селективный барьер. Мембрана защищает клетку от проникновения нежелательных частиц и веществ.

Рецепция. Через мембрану происходит распознавание других клеток, веществ.

Распространение нервного импульса. В мембране локализованы основные биоэлектрические процессы. Реализуется генерация электрического потенциала. Посредством мембраны происходит распространение нервного импульса.

Матрица. Мембрана является матрицей (основой) для удержания белков, ферментов.

Таким образом, мембрана - важнейший орган клетки, регулирующий взаимодействие как внутри клетки, так и клетки с окружающей средой. Если функции мембраны нарушаются, то происходит изменение нормального функционирования клеток и, как следствие, заболевание организма.

11.2. Структура и модели мембран

В состав мембраны входят молекулы липидов (веществ на основе жирных кислот). Молекула липида состоит из двух частей: диполь-

ной головки и углеводородного хвоста. Этот хвост представляет собой две цепочки атомов углерода, в которых к каждому из атомов углерода присоединены один или два атома водорода. По своему составу и строению эти цепочки сродни молекулам парафина и тоже не смачиваются водой, гидрофобны. Дипольные головки, напротив, гидрофильны, так как их диполи могут притягиваться к диполям воды. На рисунке 11.2 показан разрез участка мономолекулярного слоя липидного матрикса.

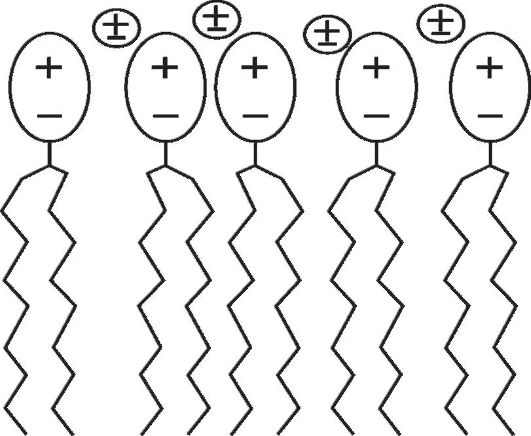Рис. 11.2. Разрез участка мономолекулярного слоя липидного матрикса; кру-

Слой не распадается по двум причинам: 1) дипольные головки притягиваются сильнее к диполям воды (взаимодействие разноименных зарядов), чем отталкиваются друг от друга (взаимодействие одноименных зарядов головок); 2) из-за наличия водородных связей между углеводородными хвостами.

Структурную основу любой мембраны составляет двойной фосфолипидный слой (рис. 11.3). Молекулы фосфолипидов ориентированы так, что их гидрофильные головки выходят наружу и образуют внешнюю и внутреннюю поверхности мембраны, а гидрофобные «хвосты» обращены к середине бимолекулярного слоя, т.е. внутрь мембраны. Гидрофильные головки взаимодействуют с внешними белковыми слоями и молекулами воды вне и внутри клетки и образуют с ними водородные связи.

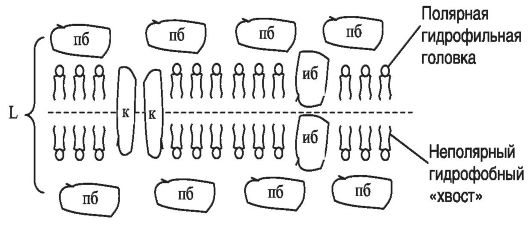Рис. 11.3. Схематичное строение мембраны:

L - толщина мембраны; пб - поверхностные белки; иб - интегральные белки; к - белки, формирующие ионный канал (пору)

Двойной фосфолипидный слой выполняет функции матрицы для различных белков (на одну молекулу белка приходится 75-90 молекул липидов). Белки как бы плавают в липидном слое.

Поверхностные белки (пб). Эти белки располагаются на внешней и внутренней поверхностях мембраны, удерживаясь преимущественно электростатическими силами. Такие белки занимают 75-80 % поверхности. Белковые молекулы покрывают мембрану с обеих сторон и придают ей эластичность и устойчивость к механическим повреждениям.

Интегральные белки (иб). Эти белки могут пронизывать двойной слой липидов насквозь. Такие белки являются главным компонентом, ответственным за избирательную проницаемость клеточной мембраны. Некоторые из них (к) образуют систему селективных каналов (пор) или функционируют как ионные насосы и регулируют, например, электрохимическую систему возбуждения клетки. Диаметр каналов составляет 0,35-0,8 нм. Количество их относительно невелико (например, в эритроцитах вся площадь каналов составляет 0,06 % от площади поверхности). Полярные группы молекул белков в каналах направлены в сторону отверстия каналов, а неполярные вступают во взаимодействие с молекулами липидов. Стенки каналов обладают электрическими зарядами.

Модели мембран

Уточнение строения биомембран и изучение их свойств осуществляются с использованием физико-химических моделей мембраны.

Первая модель - монослой. Молекулы фосфолипидов, будучи помещенными на границу раздела вода-воздух (вода-масло), выстраиваются в один слой так, что гидрофильные (полярные) головки погружаются в воду, а гидрофобные «хвосты» в контакт с водой не вступают, остаются в воздухе (масле). Молекулы фосфолипидов как бы «отслаиваются» от воды. Пока молекул немного, они располагаются на поверхности, «прильнув» к воде головками и выставив наружу хвосты (рис. 11.4, а).

Вторая модель - плоский бислой. Если в водном растворе липидных молекул становится больше, то эти молекулы собираются вместе так, что гидрофобные углеводородные цепи закрыты от воды, а полярные головки, наоборот, выставлены в воду (рис. 11.4, б). Такая модель позволяет изучать ионную проницаемость, генерацию электрического потенциала на мембране.

Третья модель - однослойная липосома. Липидные бислои, если они имеют большую протяженность, стремятся замкнуться сами на себя, чтобы спрятать гидрофобные «хвосты» от воды. При этом образуются фосфолипидные везикулы - однослойные липосомы (рис. 11.4, в). Они представляют собой мельчайшие пузырьки (везикулы), состоящие из билипидной мембраны. Липосомы фактически являются биологической мембраной, полностью лишенной белковых молекул. На липосомах часто проводят эксперименты по изучению влияния различных факторов на свойства мембраны или, наоборот, влияния мембранного окружения на свойства встраиваемых белков.

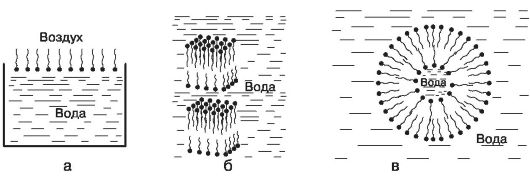Рис. 11.4. Модели молекул фосфолипидов в воде:

а - монослой, б - плоский бислой, в - однослойная липосома

В медицине липосомы используются для доставки лекарственных веществ в определенные органы и ткани. Таким способом готовятся липосомальные кремы и мази в дерматологии и косметологии. Сами липосомы нетоксичны, полностью усваиваются в организме и являются надежной липидной микрокапсулой для направленной доставки лекарства.

11.3. Физические свойства мембран

Плотность липидного бислоя составляет 800 кг/м³, что меньше, чем у воды.

Размеры. По данным электронной микроскопии, толщина мембраны (L) варьирует от 4 до 13 нм, причем различным клеточным мембранам присуща разная толщина.

Прочность. Предел прочности на разрыв для мембраны низок. В условиях организма средние деформации составляют около 0,01 %. Чтобы довести мембрану до разрыва, достаточно внутреннего давления 100 Па. Живая клетка может осуществлять осморегуляцию только за счет изменения своей формы, но не за счет растяжения мембраны.

Деформируемость. Клеточная мембрана легко подвергается деформации сдвига. Например, в потоке эритроцитов с градиентом скорости происходит вращение мембраны вокруг содержимого клетки. Это явление получило название «феномена гусеницы танка». Мембрана обладает высокой гибкостью. При оценке механических свойств мембраны эффективный модуль упругости принимается равным 0,45 Па.

Вязкость. Липидный слой мембраны имеет вязкость η = 30-100 мПас (что соответствует вязкости растительного масла).

Поверхностное натяжение равно 0,03-3 мНм^-1, что на 2-3 порядка ниже, чем у воды (73 мНм^-1).

Коэффициент проницаемости мембранного вещества для воды равен 25-33х10^-4 см/с.

Мембрана - конденсатор. Двойной фосфолипидный слой уподобляет мембрану плоскому конденсатору, обкладки которого образованы электролитами внеклеточного и внутриклеточного (цитоплазмы) растворами с погруженными в них поверхностными белками и голов-

ками липидных молекул. Обкладки разделены диэлектрическим слоем, образованным неполярной частью липидных молекул - двойным слоем их хвостов. Электроемкость 1 см² мембраны составляет 0,5-1,3 мкФ. Напряженность электрического поля в мембране составляет приблизительно 20х10⁶ В/м (расчет проведен для мембран митохондрий в задаче 2).

Диэлектрическая проницаемость мембраны составляет: для фосфолипидной области ε = 2,0-2,2; для гидрофильной области ε = 10-20.

Электросопротивление 1 см² поверхности мембраны составляет 10²-10⁵ Ом (что в десятки миллионов раз больше сопротивления внеклеточной жидкости или цитоплазмы). Электроизоляционные свойства мембраны значительно превосходят свойства технических изоляторов.

Жидкокристаллическое состояние. Молекулы в мембране размещены не беспорядочно, в их расположении наблюдается дальний порядок. Фосфолипидные молекулы находятся в двойном слое, а их гидрофобные хвосты приблизительно параллельны друг другу. Есть порядок и в ориентации полярных гидрофильных головок. Физическое состояние, при котором есть дальний порядок во взаимной ориентации и расположении молекул, но агрегатное состояние жидкое, называется жидкокристаллическим состоянием.

Жидкокристаллические структуры очень чувствительны к изменению температуры. В мембранных фосфолипидах при понижении температуры происходит переход из жидкокристаллического в гельсостояние. При этом изменяется взаимное положение гидрофобных хвостов (рис. 11.5) и увеличивается толщина двойного слоя.

При переходе в гель-состояние в бислое образуются сквозные каналы, радиусом 1-3 нм, по которым через мембрану могут переноситься ионы и низкомолекулярные вещества. Вследствие этого увеличивается ионная проводимость мембран. Увеличение ионной проводимости мембран может спасти клетку от криоповреждений за счет увеличения выхода воды и солей, что препятствует кристаллизации воды внутри клетки.

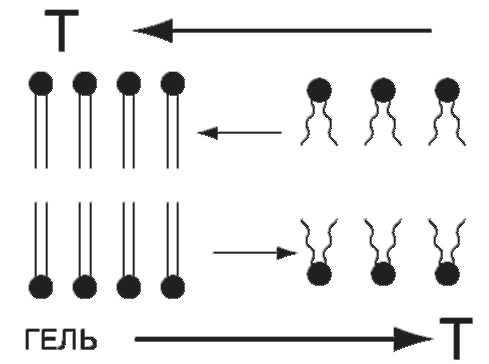Рис. 11.5. Схематическое представление мембранных фосфолипидов при изменении температуры

11.4. Перенос молекул (атомов) через мембраны, уравнение Фика

Явления переноса - самопроизвольные необратимые процессы, в которых благодаря молекулярному движению из одной части системы в другую переносится какая-либо физическая величина.

К явлениям переноса, в частности, относятся диффузия (перенос массы) и электропроводность (перенос электрического заряда).

Как синоним переноса частиц в биофизике используется термин транспорт частиц.

Уравнение диффузии в однородной среде

Рассмотрим ситуацию, когда в однородную жидкую (газообразную) среду введено некоторое количество инородного вещества. Вначале распределение этого вещества по объему жидкости будет неравномерным. Однако с течением времени вследствие явлений переноса концентрации этого вещества в различных областях жидкости будут выравниваться.

Диффузия в однородной среде - явление самопроизвольного переноса массы вещества из области с большей концентрацией в область с меньшей концентрацией. Такой перенос называется пассивным транспортом.

Количественно диффузия описывается специальными параметрами.

1. Поток вещества через некоторую поверхность.

В пространстве, заполненном частицами диффундирующего вещества, выделим некоторое направление ОХ, вдоль которого изменяется концентрация частиц, и небольшой элемент поверхности, перпендикулярный этому направлению.

Потоком вещества (Ф) через элемент поверхности, который перпендикулярен направлению диффузии, называется количество этого вещества, переносимого через данный элемент за единицу времени.

Количество переносимого вещества можно измерять в килограммах или молях (ν). В зависимости от этого поток определяется формулами:

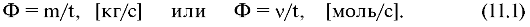Очевидно, что поток пропорционален площади S выделенного элемента. Кроме того, можно показать, что поток пропорционален градиенту концентрации (dc/dx) диффундирующего вещества в направлении ОХ. Поэтому имеет место следующая формула для расчета потока:

Коэффициент пропорциональности D называется коэффициентом диффузии. Знак «-» означает, что поток направлен в сторону убывания концентрации вещества (т.е. перенос происходит из области с большей концентрацией в область с меньшей концентрацией).

В формуле (11.2) можно использовать как массовую плотность, так и молярную плотность. Этим и определяется единица измерения потока (кг/с или моль/с). Независимо от единиц плотности размерность коэффициента диффузии D - [м²/с].

Коэффициент D зависит от свойств жидкости, свойств диффундирующих частиц, температуры. Его численное значение выражается формулой: D = σ²/(3τ), где σ - среднее перемещение молекул (среднее расстояние между молекулами), τ - среднее время «оседлой жизни» молекулы.

2. Плотность потока вещества.

Плотностью потока вещества (J) называется отношение потока вещества (Ф) через элемент поверхности к площади этого элемента (S):

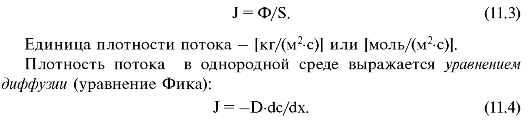Знак «-» показывает, что суммарная плотность потока вещества при диффузии направлена в сторону, противоположную градиенту концентрации (dc/dx).

Уравнение Фика для мембраны

Уравнение Фика описывает диффузию в однородной среде. Модифицируем его для случая диффузии через мембрану. Обратим внимание на следующий известный факт: на границе раздела двух сред (например, воды и масла) обязательно имеет место скачкообразное изменение концентрации частиц диффундирующего вещества. Например, если в сосуд, в котором поверх воды налито масло, бросить соль, то ее концентрации в этих средах будут различны.

Коэффициент распределения вещества (К) - величина, равная отношению концентраций частиц в граничащих средах:

Коэффициент распределения вещества - величина безразмерная.

Рассмотрим диффузию незаряженных частиц (молекул или атомов) через поверхности мембраны. На рисунке 11.6 обозначены:

с_i - концентрация частиц внутри клетки (i - от in);

с_мi - концентрация частиц в мембране у ее внутренней поверхности;

с_мо - концентрация частиц в мембране у ее внешней поверхности;

с_о - концентрация частиц вне клетки (о - от out).

Коэффициент распределения вещества между мембраной и окружающей средой равен коэффициенту распределения вещества между мембраной и клеткой:

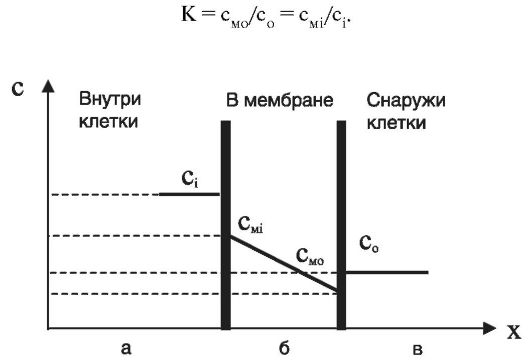Рис. 11.6. Распределение концентрации частиц, проходящих через мембрану

Отсюда получаются выражения для концентрации частиц внутри мембраны:

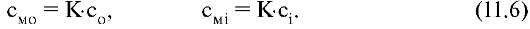Величины с_о и с можно измерить.

Учитывая малую толщину мембраны (L), можно считать, что концентрация молекул диффундирующего вещества изменяется в ней линейно. Поэтому градиент концентрации диффундирующего вещества постоянен:

Коэффициент проницаемости Р характеризует способность мембраны пропускать те или иные вещества.

11.5. Перенос заряженных частиц, электродиффузное уравнение Нернста-Планка

Уравнение Фика описывает как пассивный транспорт незаряженных частиц, так и пассивный транспорт заряженных частиц в отсутствии электрического поля. Рассмотрим теперь транспорт ионов с учетом электрического поля внутри мембраны.

На отдельный ион в электрическом поле действует сила f₀ = qE, где Е - напряженность электрического поля, а q = Ze - заряд иона (Z - валентность иона). Напряженность поля выражается через градиент

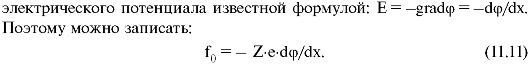Уравнению 11.11 можно придать более удобный вид, умножив обе его части на постоянную Авогадро (N_A):

Это уравнение Нернста-Планка (электродиффузное уравнение). Оно устанавливает зависимость плотности диффузного потока ионов от концентрации ионов и от градиента потенциала (dφ/dx).

Для нейтральных частиц (Z = 0) уравнение Нернста-Планка переходит в уравнение Фика.

11.6. Виды транспорта через мембрану

1. Пассивный транспорт - перенос молекул и ионов через мембрану, который осуществляется в направлении меньшей их концентрации. Пассивный транспорт не связан с затратой химической энергии. Он стремится выровнять концентрации частиц по разные стороны от мембраны, т.е. свести к нулю величины их градиентов. Если бы в клетках существовал только пассивный транспорт, то значения физической величины внутри и вне клетки сравнялись бы, но этого не происходит.

Различают несколько типов пассивного транспорта (рис. 11.7).

•  Простая диффузия через липидный слой. Она подчиняется уравнению Нернста-Планка. В живой клетке такая диффузия обеспечивает прохождение кислорода и углекислого газа, ряда лекарственных веществ. Однако простая диффузия протекает достаточно медленно и не может снабдить клетку в нужном количестве питательными веществами.

•  Транспорт через каналы (поры). Канал - участок мембраны, включающий белковые молекулы и липиды, который образует в мембране проход. Этот проход допускает проникновение через мембрану молекул воды, крупных ионов. Наличие каналов увеличивает проницаемость Р. Проницаемость Р зависит от числа каналов и от их радиуса. Каналы могут проявлять селективность

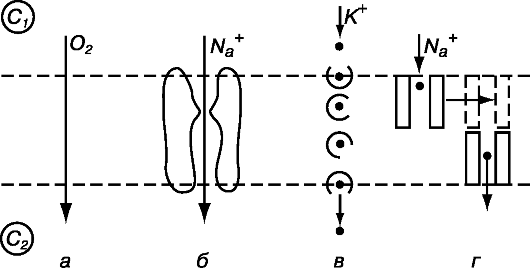Рис. 11.7. Виды пассивного транспорта: простая диффузия (а), транспорт через каналы (б), облегченная диффузия (в), эстафетная передача (г)

по отношению к разным ионам, это выражается в различной проницаемости для разных ионов.

•  Облегченная диффузия - перенос ионов специальными молекулами-переносчиками за счет диффузии переносчика вместе с веществом. Наиболее подробно это явление изучено для случая переноса ионов некоторыми антибиотиками, например валиномицином. Установлено, что валиномицин резко повышает проницаемость мембраны для ионов К+ благодаря специфике своей структуры. В нем формируется полость, в которую точно и прочно вписывается ион К⁺ (ион Na⁺ слишком велик для отверстия в молекуле валиномицина). Молекула валиномицина, «захватив» ион К⁺, образует растворимый в липидах комплекс и проходит через мембрану, затем ион К⁺ остается, а переносчик уходит обратно.

•  Эстафетная передача. В этом случае молекулы-переносчики образуют временную цепочку поперек мембраны и передают друг другу диффундирующую молекулу.

2. Активный транспорт - перенос молекул и ионов, который происходит с затратой химической энергии в направлении от меньших значений величин к большим. При этом нейтральные молекулы переносятся в область большей концентрации, а ионы переносятся против сил, действующих на них со стороны электрического поля. Таким образом, активным транспортом осуществляется перенос веществ в направлении, противоположном транспорту, который должен был бы происходить под действием градиентов (прежде всего концентрационного и электрического). Энергия получается за счет гидролиза молекул особого химического соединения - аденозинтрифосфорной кислоты (АТФ). Экспериментально установлено, что энергии распада одной молекулы АТФ достаточно для выведения наружу трех ионов натрия и введения внутрь клетки двух ионов калия. Одна из схем активного транспорта представлена системой на рис. 11.8.

Захватив одним активным центром ион калия из наружной среды, а другим ион натрия - из внутренней, система, потребляя АТФ, поворачивается внутри мембраны на 180°. Ион натрия оказывается вне клетки и там отделяется, а ион калия попадает внутрь и тоже освобождается, после чего молекула белка принимает исходное положение, и все начинается сначала.

За счет активного транспорта клетка поддерживает внутри себя высокую концентрацию калия и низкую концентрацию натрия. При

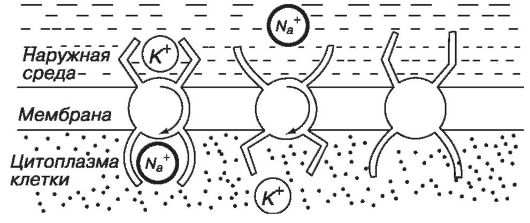Рис. 11.8. Схема активного транспорта

этом ионы могут перемещаться против градиента их концентрации (аналогия с газом: перекачивание газа из сосуда с низким давлением в сосуд с высоким давлением).

Активный транспорт обеспечивает механизм селективной проницаемости клеточных мембран. Активный транспорт - важнейшая особенность жизненных процессов.

11.7. Основные понятия и формулы

Окончание таблицы

11.8. Задачи

1. Молярная концентрация кислорода в атмосфере с_а = 9 моль/м³. Кислород диффундирует с поверхности тела насекомых внутрь через трубки, называемые трахеями. Длина средней трахеи равна приблизительно h = 2 мм, а площадь ее поперечного сечения S = 2х10^-9 м². Считая, что концентрация кислорода внутри насекомого (с) в два раза меньше, чем концентрация кислорода в атмосфере, вычислить поток диффузии через трахею. Коэффициент диффузии кислорода D = 10^-5 м²/с.

Решение

Запишем уравнение (11.2) для потока диффузии: Ф = -DSdc/dx. Градиент концентрации dc/dx = (с - с_a)/h = (0,5с - с)/h = -0,5с/h = = 0,5x9/0,002 = 225 моль/м⁴. Подставив численные значения, получим:

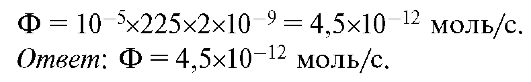2. Двойной фосфолипидный слой уподобляет биологическую мембрану конденсатору. Вещество мембраны представляет собой диэлектрик с диэлектрической проницаемостью ε = 4. Разность потенциалов между поверхностями мембраны U = 0,2 В при толщине d = 10 нм. Рассчитать электроемкость 1 мм² мембраны и напряженность электрического поля в ней.

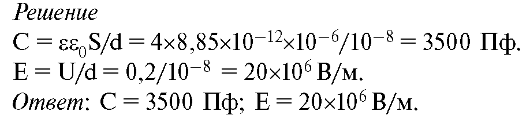3. Площадь поверхности клетки приблизительно равна S =5х10^-1° м². Удельная электроемкость мембраны (емкость единицы поверхности) составляет С_уд = 10^-2 Ф/м². При этом межклеточный потенциал равен U = 70 мВ. Определить: а) величину заряда на поверхности мембраны; б) количество одновалентных ионов, образующих этот заряд.

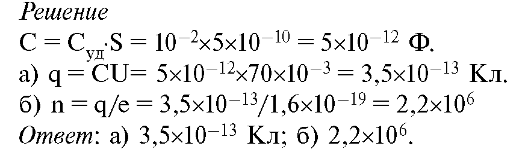4. Проницаемость клеточных мембран для молекул воды приблизительно в 10 раз выше, чем для ионов. Что произойдет, если в изотоническом водном растворе, в котором находятся эритроциты, увеличить концентрацию осмотически активного вещества (например, ионов

Решение

Повышение концентрации ионов Na⁺ в растворе приведет к диффузии воды из клеток в окружающий раствор для восстановления нарушенного соотношения концентрации Na⁺ внутри и вне клетки. В результате клетки «сморщиваются».

5. Что будет, если клетку поместить в чистую воду? Решение

В этом случае окажется, что концентрация молекул воды снаружи выше, чем внутри клетки. Молекулы воды будут диффундировать в клетку. Внутреннее давление будет расти, пока клетку не разорвет.