ЛЕКЦИЯ 8 ВЯЗКОСТЬ ЖИДКОСТИ

7. Влияние вязкости на некоторые медицинские процедуры. Ламинарность и турбулентность газового потока при наркозе. Введение жидкостей через капельницу и шприц. Риноманометрия. Фотогемотерапия.

8. Основные понятия и формулы.

9. Задачи.

Гидродинамика - раздел физики, в котором изучают вопросы движения несжимаемых жидкостей и их взаимодействие с окружающими телами.

8.1. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона

В реальной жидкости вследствие взаимного притяжения и теплового движения молекул имеет место внутреннее трение, или вязкость. Рассмотрим это явление на следующем опыте (рис. 8.1).

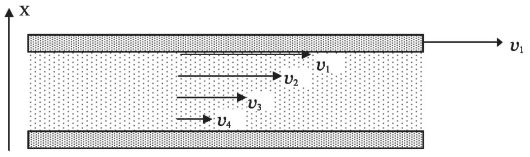Рис. 8.1. Течение вязкой жидкости между пластинами

Поместим слой жидкости между двумя параллельными твердыми пластинами. «Нижняя» пластина закреплена. Если двигать «верхнюю» пластину с постоянной скоростью v₁, то c такой же скоростью будет двигаться самый «верхний» 1-й слой жидкости, который считаем «прилипшим» к верхней пластине. Этот слой влияет на нижележащий непосредственно под ним 2-й слой, заставляя его двигаться со скоростью v₂, причем v₂ < v₁. Каждый слой (выделим n слоев) передает движение нижележащему слою с меньшей скоростью. Слой, непосредственно «прилипший» к «нижней» пластине, остается неподвижным.

Слои взаимодействуют друг с другом: n-й слой ускоряет (п+1)-й слой, но замедляет (п-1)-й слой. Таким образом, наблюдается изменение скорости течения жидкости в направлении, перпендикулярном поверхности слоя (ось х). Такое изменение характеризуют производной dv/dx, которую называют градиентом скорости.

Силы, действующие между слоями и направленные по касательной к поверхности слоев, называются силами внутреннего трения или вязкости. Эти силы пропорциональны площади взаимодействующих слоев S и градиенту скорости. Для многих жидкостей силы внутреннего трения подчиняются уравнению Ньютона:

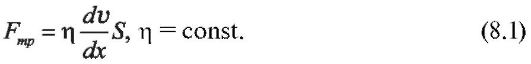Коэффициент пропорциональности η называют коэффициентом внутреннего трения или динамической вязкостью (размерность η в СИ: Пас).

8.2. Ньютоновские и неньютоновские жидкости.

Кровь

Ньютоновская жидкость

Жидкость, которая подчиняется уравнению Ньютона (8.1), называют ньютоновской. Коэффициент внутреннего трения ньютоновской жидкости зависит от ее строения, температуры и давления, но не зависит от градиента скорости.

Ньютоновская жидкость - жидкость, вязкость которой не зависит от градиента скорости.

Свойствами ньютоновской жидкости обладают большинство жидкостей (вода, растворы, низкомолекулярные органические жидкости) и все газы.

Вязкость определяется с помощью специальных приборов - вискозиметров. Значения коэффициента вязкости η для некоторых жидкостей представлены в таблице.

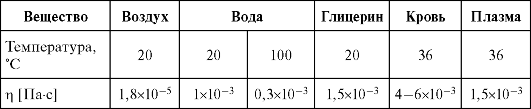Значение вязкости крови, представленное в таблице, относится к здоровому человеку в спокойном состоянии. При тяжелой физической работе вязкость крови увеличивается. На величину вязкости крови влияют и некоторые заболевания. Так, при сахарном диабете вязкость крови увеличивается до 23?10^-3 Пас, а при туберкулезе уменьшается до 1*10^-3Пас. Вязкость сказывается на таком клиническом параметре, как скорость оседания эритроцитов (СОЭ).

Неньютоновская жидкость

Неньютоновская жидкость - жидкость, вязкость которой зависит от градиента скорости.

Свойствами неньютоновской жидкости обладают структурированные дисперсные системы (суспензии, эмульсии), растворы и расплавы некоторых полимеров, многие органические жидкости и др.

При прочих равных условиях вязкость таких жидкостей значительно больше, чем у ньютоновских жидкостей. Это связано с тем, что благодаря сцеплению молекул или частиц в неньютоновской жидкости образуются пространственные структуры, на разрушение которых затрачивается дополнительная энергия.

Кровь

Цельная кровь (суспензия эритроцитов в белковом растворе - плазме) является неньютоновской жидкостью вследствие агрегации эритроцитов.

Эритроцит в норме имеет форму двояковогнутого диска диаметром около 8 мкм. Он может существенно менять свою форму, например при различной осмолярности среды (рис. 8.2).

В неподвижной крови эритроциты агрегируют, образуя так называемые «монетные столбики», состоящие из 6-8 эритроцитов. Электронно-микроскопическое исследование тончайших срезов монетных столбиков выявило параллельность поверхностей прилежащих эритроцитов и постоянное межэритроцитарное расстояние при агрегации (рис. 8.3).

На рисунке 8.4 показана (зарисовка) агрегация цельной крови во влажных мазках, которая представляет собой большие конгломераты, состоящие из многих монетных столбиков. При перемешивании крови агрегаты разрушаются, а после прекращения перемешивания вновь восстанавливаются.

При протекании крови по капиллярам агрегаты эритроцитов распадаются и вязкость падает.

Вживление специальных прозрачных окошек в кожные складки позволило сфотографировать течение крови в капиллярах. На рисунке 8.5, выполненном по такой фотографии, отчетливо видна деформация кровяных клеток.

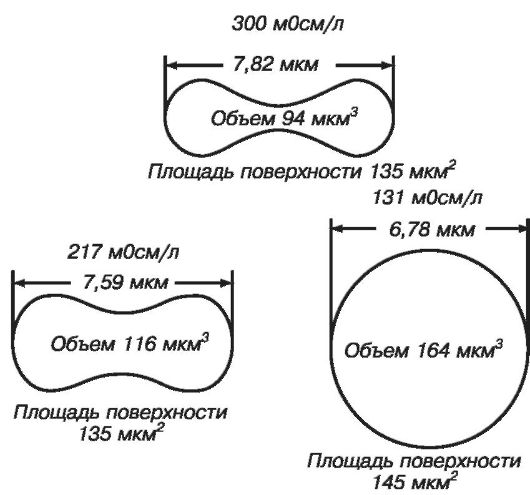Рис. 8.2. Усредненное поперечное сечение эритроцита при различной осмолярности среды

Рис. 8.3. Схема электроннограммы агрегата из нормальных эритроцитов

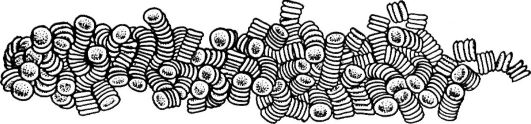Рис. 8.4. Агрегация цельной крови

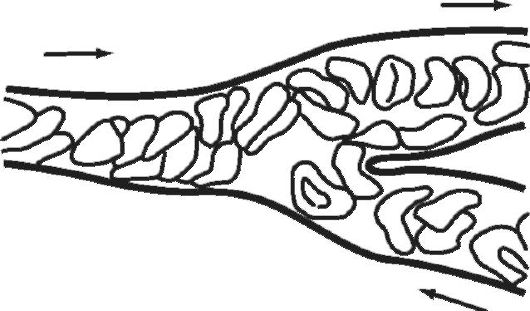Рис. 8.5. Деформация эритроцитов в капиллярах

Деформируясь, эритроциты могут продвигаться один за другим в капиллярах диаметром всего 3 мкм. Именно в таких тонких капиллярных сосудах и происходит газообмен между кровью и тканями.

Вблизи стенки капилляра образуется очень тонкий слой плазмы, который играет роль смазки. Благодаря этому сопротивление движению эритроцитов уменьшается.

8.3. Ламинарное и турбулентное течения, число Рейнольдса

В жидкости течение может быть ламинарным или турбулентным. На рисунке 8.6 это показано для одной окрашенной струи жидкости, текущей в другой.

В случае (а) струя окрашенной жидкости сохраняет неизменную форму и не смешивается с остальной жидкостью. В случае (б) окрашенная струя разрывается случайными завихрениями, картина которых меняется с течением времени. К турбулентному течению понятие «трубка тока» неприменимо.

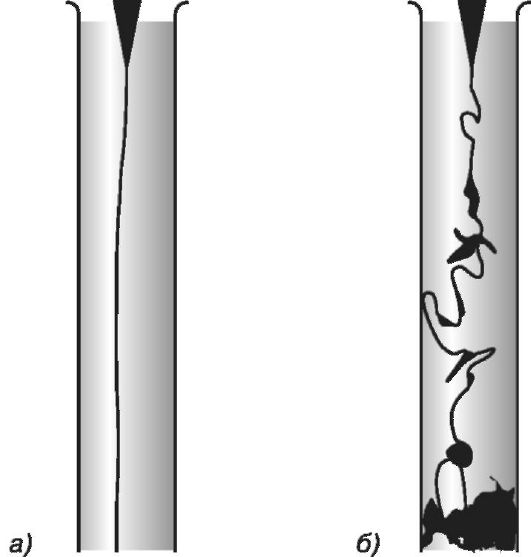Рис. 8.6. Ламинарное (а) и турбулентное (б) течения струи жидкости

Ламинарное (слоистое) течение - такое течение, при котором слои жидкости текут, не перемешиваясь, скользя друг относительно друга. Ламинарное течение является стационарным - скорость течения в каждой точке пространства остается постоянной.

Рассмотрим ламинарное течение ньютоновской жидкости в трубе радиуса R и длины L, давления на концах которой постоянны (Р₁ и Р₂). Выделим цилиндрическую трубку тока радиуса r (рис. 8.7).

На жидкость внутри этой трубки действуют сила давления F_д = πг²(Р₁ - Р₂) и сила вязкого трения F_тр = 2πrLηdv/dr (2πrL - пло-

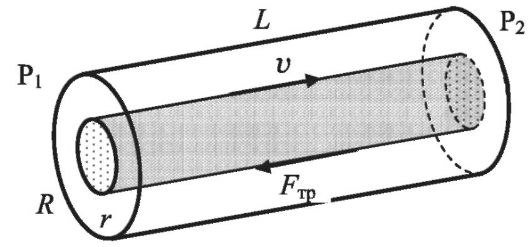Рис. 8.7. Трубка тока и действующая на нее сила трения

щадь боковой поверхности). Так как течение стационарное, сумма этих сил равна нулю:

В соответствии с приведенным выражением имеет место параболическая зависимость скорости v слоев жидкости от расстояния от них до оси трубы r (огибающая всех векторов скорости есть парабола) (рис. 8.8).

Наибольшую скорость имеет слой, текущий вдоль оси трубы (r = 0), слой, «прилипший» к стенке (r = R), неподвижен.

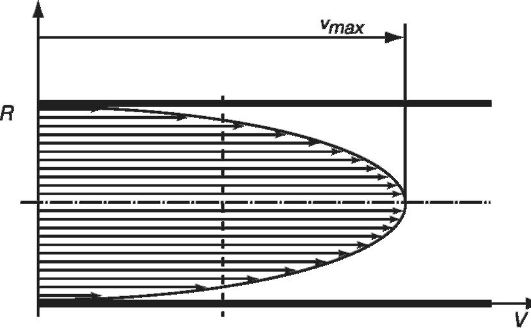Рис. 8.8. Скорости слоев текущей через трубку жидкости распределены по параболе

Турбулентное (вихревое) течение - такое течение, при котором скорости частиц жидкости в каждой точке беспорядочно меняются. Такое движение сопровождается появлением звука. Турбулентное течение - это хаотическое, крайне нерегулярное, неупорядоченное течение жидкости. Элементы жидкости совершают движение по сложным неупорядоченным траекториям, что приводит к перемешиванию слоев и образованию местных завихрений.

Структура турбулентного течения представляет собой нестационарную совокупность очень большого числа малых вихрей, наложенных на основное «среднее течение».

При этом говорить о течении в ту или иную сторону можно только в среднем за какой-то промежуток времени.

Турбулентное течение связано с дополнительной затратой энергии при движении жидкости: часть энергии расходуется на беспорядочное движение, направление которого отличается от основного направления потока, что в случае крови приводит к дополнительной работе сердца. Шум, возникающий при турбулентном течении крови, может быть использован для диагностирования заболевания. Этот шум прослушивается, например, на плечевой артерии при измерении давления крови.

Турбулентное движение крови может возникнуть вследствие неравномерного сужения просвета сосуда (или локального выпирания). Турбулентное течение создает условия для оседания тромбоцитов и образования агрегатов. Этот процесс часто является пусковым

в формировании тромба. Кроме того, если тромб слабо связан со стенкой сосуда, то под действием резкого перепада давления вдоль него вследствие турбулентности он может начать двигаться.

Число Рейнольдса

Понятия ламинарности и турбулентности применимы как к течению жидкости по трубам, так и к обтеканию ею различных тел. В обоих случаях характер течения зависит от скорости течения, свойств жидкости и характерного линейного размера трубы или обтекаемого тела.

Английский физик и инженер Осборн Рейнольдс (1842-1912) составил безразмерную комбинацию, величина которой и определяет характер течения. Впоследствии эта комбинация была названа числом Рейнольдса (Re):

Число Рейнольдса используют при моделировании гидро- и аэродинамических систем, в частности кровеносной системы. Модель должна иметь такое же число Рейнольдса, как и сам объект, в противном случае соответствия между ними не будет.

Важным свойством турбулентного течения (по сравнению с ламинарным) является высокое сопротивление потоку. Если бы удалось «погасить» турбулентность, то удалось бы достичь огромной экономии мощности двигателей кораблей, подводных лодок, самолетов.

8.4. Формула Пуазейля, гидравлическое сопротивление

Рассмотрим, от каких факторов зависит объем жидкости, протекающей по горизонтальной трубе.

Формула Пуазейля

При ламинарном течении жидкости по трубе радиуса R и длины L объем Q жидкости, протекающей через горизонтальную трубу за одну секунду, можно вычислить следующим образом. Выделим тонкий цилиндрический слой радиуса r и толщины dr (рис. 8.9).

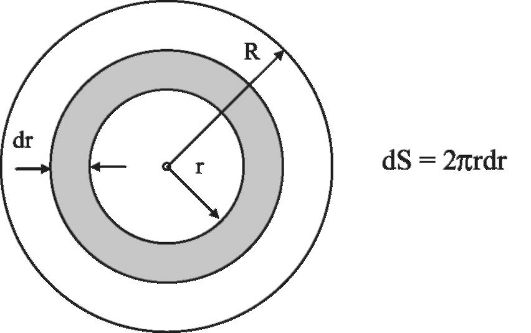Рис. 8.9. Сечение трубы с выделенным слоем жидкости

Площадь его поперечного сечения равна dS = 2πrdr. Так как выделен тонкий слой, жидкость в нем перемещается с одинаковой скоростью v. За одну секунду слой перенесет объем жидкости

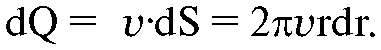Подставив сюда формулу для скорости цилиндрического слоя жидкости (8.4), получим

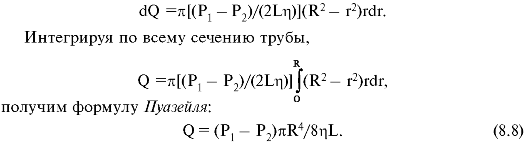Это соотношение справедливо для ламинарного течения ньютоновской жидкости.

Формулу Пуазейля можно записать в виде, справедливом для труб переменного сечения. Заменим выражение (Р₁ - Р₂)/L на градиент давления dP/d/, тогда получим

Как видно из (8.8), при заданных внешних условиях объем жидкости, протекающей по трубе, пропорционален четвертой степени ее радиуса. Это очень сильная зависимость. Так, например, если при атеросклерозе радиус сосудов уменьшится в 2 раза, то для поддержания нормального кровотока перепад давлений нужно увеличить в 16 раз, что практически невозможно. В результате возникает кислородное голодание соответствующих тканей. Этим объясняется возникновение «грудной жабы». Облегчения можно достичь, вводя лекарственное вещество, которое расслабляет мышцы артериальных стенок и позволяет увеличить просвет сосуда и, следовательно, поток крови.

Поток крови, проходящей через сосуды, регулируется специальными мышцами, окружающими сосуд. При их сокращении просвет сосуда уменьшается и соответственно убывает поток крови. Таким образом, незначительным сокращением этих мышц очень точно контролируется поступление крови в ткани.

В организме путем изменения радиуса сосудов (сужения или расширения) за счет изменения объемной скорости кровотока регулируется кровоснабжение тканей, теплообмен с окружающей средой.

Причины движения крови по сосудам

Главная движущая сила кровотока - разность давлений в начале и в конце сосудистой системы: в большом круге кровообращения - разность давлений в аорте и правом предсердии, в малом круге - в легочной артерии и левом предсердии.

Дополнителные факторы, способствующие движению крови по венам в сторону сердца:

1) полулунные клапаны вен конечностей, которые открываются под напором крови только в сторону сердца;

2) присасывающее действие грудной клетки, связанное с отрицательным давлением в ней при вдохе;

3) сокращение мышц конечностей, например, при хотьбе. При этом происходит надавливание на стенки вен, и кровь, благодаря клапанам и присасывающему действию грудной клетки при вдохе, выжимается в участки, расположенные ближе к сердцу.

Гидравлическое сопротивление

Проведем аналогию между формулой Пуазейля и формулой закона Ома для участка цепи тока: I = ΔU/R. Для этого перепишем формулу (8.8) в следующем виде: Q = (P₁ - Р₂)/[8ηL/(πR⁴)]. Если сравнить эту формулу с законом Ома для электрического тока, то объем жидкости, протекающей через сечение трубы за одну секунду, соответствует силе тока; разность давлений на концах трубы соответствует разности потенциалов; а величина 8ηL/(πR⁴) соответствует электрическому сопротивлению. Ее называют гидравлическим сопротивлением:

Гидравлическое сопротивление трубы прямо пропорционально ее длине и обратно пропорционально четвертой степени радиуса.

Если изменением кинетической энергии жидкости на некотором участке можно пренебречь, то рассмотренная аналогия применима и к потоку переменного сечения:

гидравлическим сопротивлением участка называется отношение перепада давлений к объему жидкости, протекающему за 1 секунду:

Наличие гидравлического сопротивления связано с преодолением сил внутреннего трения.

Законы гидродинамики значительно сложнее законов постоянного тока, поэтому и законы соединения труб (кровеносных сосудов) сложнее законов соединения проводников. Так, например, места резкого сужения потока (даже при небольшой длине) обладают большим собственным гидравлическим сопротивлением. Этим и объясняется значительное увеличение гидравлического сопротивления кровеносного сосуда при образовании небольшой бляшки.

Наличие собственного сопротивления у мест резкого сужения потока необходимо учитывать при расчете сопротивления участка, состоящего

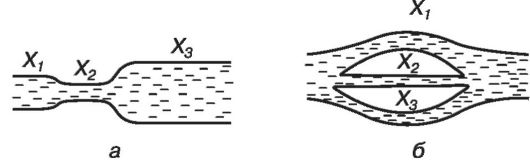Рис. 8.10. Трубы, соединенные последовательно (а) и параллельно (б)

из труб различного диаметра. На рис. 8.10,а показано последовательное сопротивление трех труб. Места сужения обладают собственным сопротивлением Х₁₂ и Х₂₃. Поэтому сопротивление участка равно

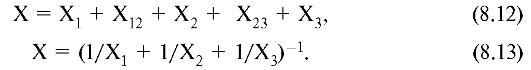Электрический аналог (8.13) формулы для расчета гидродинамического сопротивления параллельного соединения (рис 8.10, б) также требует учета сопротивлений мест соединения труб.

8.5. Распределение давления при течении реальной жидкости по трубам различного сечения

При течении по горизонтальной трубе реальной жидкости работа внешних сил расходуется на преодоление внутреннего трения. Поэтому статическое давление вдоль трубы постепенно падает. Этот эффект может быть продемонстрирован на простом опыте. Установим в разных местах горизонтальной трубы, по которой течет вязкая жидкость, манометрические трубки (рис. 8.11).

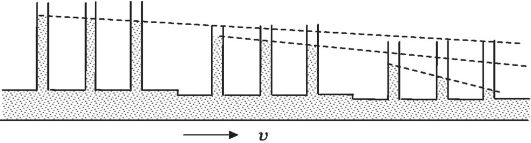Рис. 8.11. Падение давления вязкой жидкости в трубах различного сечения

Из рисунка видно, что при постоянном сечении трубы давление падает пропорционально длине. При этом скорость падения давления (dP/dl) увеличивается при уменьшении сечения трубы. Это объясняется ростом гидравлического сопротивления при уменьшении радиуса.

В кровеносной системе человека на капилляры приходится до 70 % падения давления.

8.6. Методы определения вязкости жидкостей

Совокупность методов измерения вязкости жидкости называется вискозиметрией. Прибор для измерения вязкости называется вискозиметром. В зависимости от метода измерения вязкости используют следующие типы вискозиметров.

1. Капиллярный вискозиметр Оствальда основан на использовании формулы Пуазейля. Вязкость определяется по результату измерения времени протекания через капилляр жидкости известной массы под действием силы тяжести при определенном перепаде давлений.

2. Медицинский вискозиметр Гесса с двумя капиллярами, в которых движутся две жидкости (например, дистиллированная вода и кровь). Вязкость одной жидкости должна быть известна. Учитывая, что перемещение жидкостей за одно и то же время обратно пропорционально их вязкости, вычисляют вязкость второй жидкости.

3. Вискозиметр, основанный на методе Стокса, согласно которому при движении шарика радиуса R в жидкости с вязкостью η при небольшой скорости v сила сопротивления пропорциональна вязкости этой жидкости: F = 6πηRv (формула Стокса). Эритроциты перемещаются в вязкой жидкости - плазме крови. Так как эритроциты имеют дискообразную форму и оседают в вязкой жидкости, то скорость их оседания (СОЭ) можно определить приближенно по формуле Стокса. О скорости оседания судят по количеству плазмы над осевшими эритроцитами. В норме скорость оседания эритроцитов равна: 7-12 мм/ч для женщин и 3-9 мм/ч для мужчин.

4. Вискозиметр ротационный (рис. 8.12) состоит из двух коаксиальных (соосных) цилиндров. Радиус внутреннего цилиндра - R, радиус внешнего цилиндра - R+ΔR (ΔR << R). Пространство между цилин-

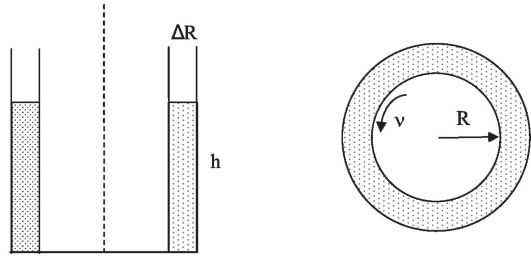Рис. 8.12. Ротационный вискозиметр (сечения вдоль и перпендикулярно оси)

драми заполняют исследуемой жидкостью до некоторой высоты h. Затем внутренний цилиндр приводят во вращение, прикладывая определенный момент сил М, и измеряют установившуюся частоту вращения ν.

Вязкость жидкости вычисляют по формуле

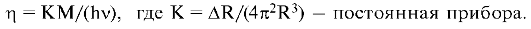Применяя ротационный вискозиметр, можно измерять вязкость при разных угловых скоростях вращения ротора. Данный метод позволяет установить зависимость между вязкостью и градиентом скорости, что важно для неньютоновских жидкостей.

8.7. Влияние вязкости на некоторые медицинские

процедуры

Наркоз

В некоторых медицинских мероприятиях используется наркоз. При этом необходимо по возможности уменьшить усилия, затрачиваемые больным на дыхание через эндотрахеальные и другие дыхательные трубки, посредством которых подается дыхательная смесь из аппаратов для наркоза (рис. 8.13).

Для обеспечения плавного газового потока используются плавно изогнутые соединительные трубки. Неровности внутренних стенок трубки, резкие изгибы и изменения внутреннего диаметра трубок

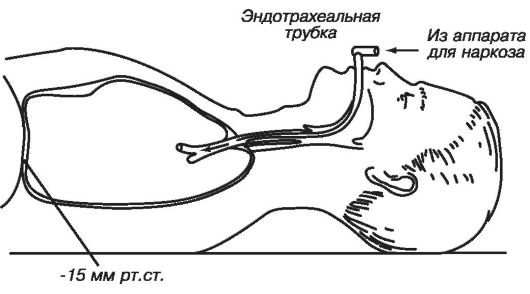Рис. 8.13. Дыхание больного через эндотрахеальную трубку

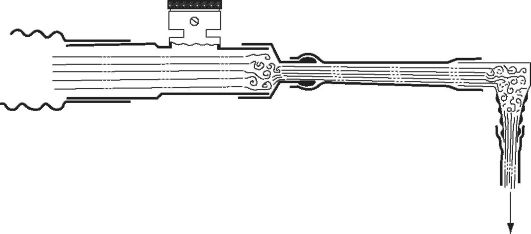Рис. 8.14. Возникновение турбулентности газового потока в трубке с резкими неоднородностями по сечению

и соединений часто являются причинами перехода ламинарного потока в турбулентный (рис. 8.14), что затрудняет процесс дыхания у больного.

На рисунке 8.15 приведен рентгеновский снимок головы больного, показывающий, что эндотрахеальная трубка перегнулась в глотке. В данном случае у больного обязательно возникнут затруднения дыхания.

Введение жидкостей через шприц и капельницу

Шприц - очень простой прибор (рис. 8.16), который используют для инъекций. И тем не менее при описании его работы часто допускается ошибка, связанная с нахождением перепада давлений (ΔР) на игле, которая приводит к неверному результату. Считают, что

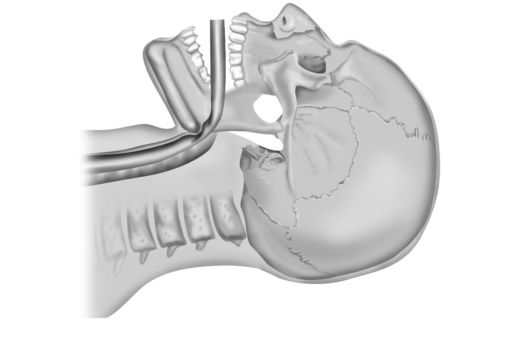Рис. 8.15. Рентгеновский снимок, на котором виден перегиб дыхательной трубки

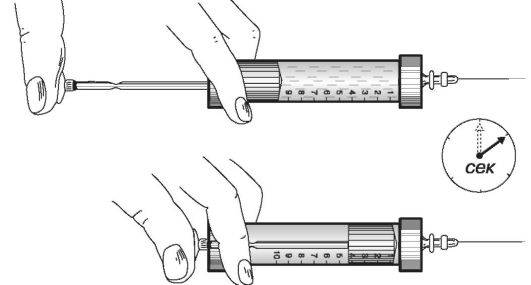Рис. 8.16. Работа шприца

ΔP = F/S, где F - сила, действующая на поршень, а S - его площадь. При этом исходят из следующих соображений: поршень движется медленно и динамическим давлением жидкости в цилиндре можно

пренебречь. Это неверно - на входе в иглу линии тока сгущаются и скорость движения жидкости резко возрастает.

Строгий расчет (см. задачу 8.12) приводит к следующему результату. Перепад давления на игле (ΔР) является решением квадратного уравнения

Значения всех величин подставляются в СИ.

Ниже приводятся результаты расчетов для двух игл длины 4 см, диаметры которых отличаются в 1,5 раза.

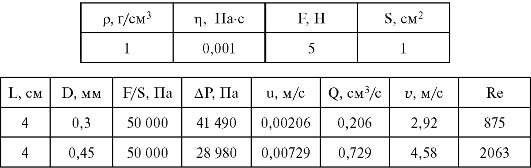Из результатов, представленных в нижней таблице, видно, что АР вовсе не равно F/S! При этом увеличение диаметра иглы в 1,5 раза приводит к увеличению объемной скорости всего в 3,5 раза, а не в 5 раз (1,5⁴ = 5,06), как этого можно было ожидать. Ламинарный характер течения имеет место в обоих случаях.

Другим прибором для внутривенного вливания является капельница (рис. 8.17), которая позволяет вводить жидкость самотеком за счет разности давлений, создаваемой при подъеме камеры с препаратом на определенную высоту (~60 см).

Формулы 8.14, 8.15 применимы и здесь, если заменить величину F/S на гидростатическое давление столба жидкости pgh. При этом S - площадь сечения трубки, а u - скорость движения жидкости в ней. Ниже приведены результаты расчетов для h = 60 см.

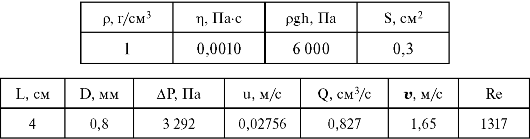Полученные значения являются правильными, но не соответствуют тому, что происходит на самом деле. В данном случае получается завышенное значение для объемной скорости ввода препарата - 0,827 см³/с. Реальная скорость Q = 0,278 см³/с (из расчета 500 мл за 30 минут). Расхождение получается из-за того, что не учтено гидравлическое сопротивление, создаваемое устройством, пережимающим трубку.

Риноманометрия

Полноценное носовое дыхание является необходимой предпосылкой для нормальной функции слуховой трубы, которая во многом зависит от степени аэрации носоглотки и правильного прохождения воздушных потоков в полости носа. Причиной нарушения носового дыхания часто являются некоторые врожденные патологии, например расщелина верхней губы и неба. Часто при лечении этой патологии

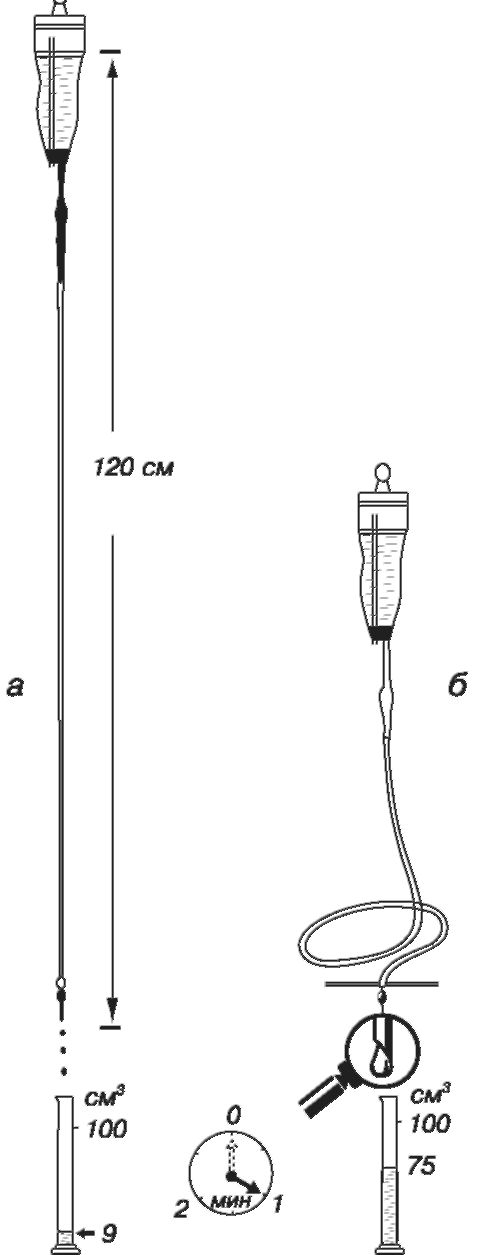Рис. 8.17. Введение препарата через капельницу

используются хирургические методы, например реконструктивная ринохейлопластика (ринопластика - операции восстановления носа). Для объективной характеристики результатов оперативного вмешательства используется риноманометрия - метод определения объема носового дыхания и сопротивления. Скорость воздушного потока характеризуется формулой Пуазейля, при этом учитывается градиент давления, обусловленный изменением давления в носоглоточном пространстве; диаметр и длина носовой полости; характеристики воздушного потока в носоглотке (ламинарность или турбулентность). Данный метод реализуется с помощью прибора - риноманометра, который позволяет регистрировать давление в одной половине носа, пока пациент дышит через другую. Это осуществляется с помощью катетера, который специально крепится в носу. Компьютерная схема риноманометра позволяет автоматически измерить общий объем и сопротивление воздуха на вдохе и выдохе, раздельно проанализировать поток и сопротивление воздуха в каждой половине носа и рассчитать их соотношение. Это позволяет определить носовое дыхание до и после операции и оценить степень восстановления носового дыхания.

Фотогемотерапия

При заболеваниях, сопровождающихся повышением вязкости крови, для уменьшения вязкости крови применяется метод фотогемотерапии. Он заключается в том, что у больного берут небольшое количество крови (примерно 2 мл/кг веса), подвергают ее УФ-облучению и вводят обратно в кровеносное русло. Примерно через 5 мин после введения больным 100-200 мл облученной крови наблюдается значительное снижение вязкости во всем объеме (около 5 л) циркулирующей крови. Исследования зависимости вязкости от скорости движения крови показали, что при фотогемотерапии вязкость сильнее всего снижается (примерно на 30 %) в медленно движущейся крови и совсем не меняется в быстро движущейся крови. УФ-облучение вызывает снижение способности эритроцитов к агрегации и увеличивает деформируемость эритроцитов. Помимо этого происходит снижение образования тромбов. Все эти явления приводят к значительному улучшению как макро-, так и микроциркуляции крови.

8.8. Основные понятия и формулы

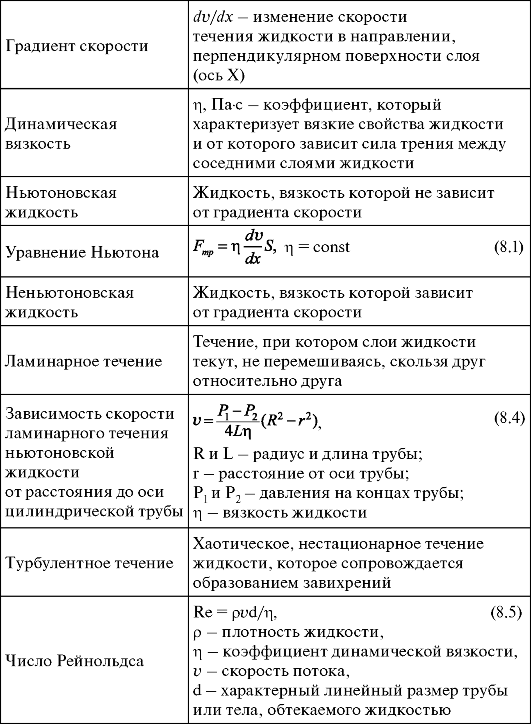Окончание таблицы

8.9. Задачи

1. Вывести формулу для определения вязкости ротационным вискозиметром. Дано: R, ΔR, h, ν, M.

2. Определить время протекания крови через капилляр вискозиметра, если вода протекает через него за 10 с. Объемы воды и крови одинаковы. Плотность воды и крови равны p₁ = 1 г/см³, ρ₂ = 1,06 г/см³. Вязкость крови относительно воды равна 5 (η₂/η₁ = 5).

3. Допустим, что в двух кровеносных сосудах градиент давления одинаков, а поток крови (объемный расход) во втором сосуде на 80% меньше, чем в первом. Найти отношение их диаметров.

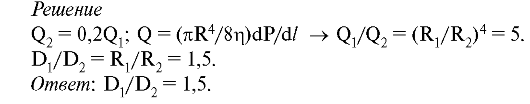4. Какова должна быть разность давлений АР на концах капилляра радиуса r = 1 мм и длины L = 10 см, чтобы за время t = 5 с через него можно было пропустить объем V = 1 см³ воды (коэффициент вязкости η₁ = 10^-3 Пас) или глицерина (η₂ = 0,85 Пас)?

5. Падение давления в кровеносном сосуде длины L = 55 мм и радиуса r = 1,5 мм равно 365 Па. Определить, сколько миллилитров крови протекает через сосуд за 1 минуту. Коэффициент вязкости крови η = 4,5 мПа-с.

6. При атеросклерозе, вследствие образования бляшек на стенках сосуда, критическое значение числа Рейнольдса может снизиться до 1160. Определить для этого случая скорость, при которой возможен переход ламинарного течения крови в турбулентное в сосуде диаметром 2,5 мм. Плотность крови равна ρ = 1050 кг/м³, вязкость крови равна η = 5х10^-3 Пас.

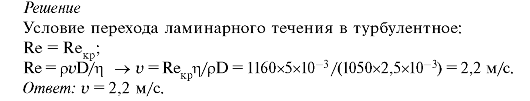7. Средняя скорость крови в аорте радиусом 1 см равна 30 см/с. Выяснить, является ли данное течение ламинарным? Плотность крови ρ = 1,05х10³ кг/м³.

η = 4х10^-3 Па-с; Rе_кр = 2300.

8. При большой физической нагрузке скорость кровотока иногда увеличивается вдвое. Пользуясь данными примера задачи (7), определить характер течения в этом случае.

Решение

Re = 2x1575 = 3150. Течение турбулентное.

Ответ: число Рейнольдса больше критического значения, поэтому течение может стать турбулентным.

9. Рассчитать число Рейнольдса для течения крови в капилляре, если скорость течения равна 0,5 мм/с, а диаметр капилляра 0,1 мм. Плотность крови ρ = 1050 кг/м³, η = 4x10^-3 Па-с.

10. Определить максимальную массу крови, которая может пройти за 1 с через аорту при сохранении ламинарного характера течения. Диаметр аорты D = 2 см, вязкость крови η = 4x10^-3 Па-с.

11. Определить максимальную объемную скорость протекания жидкости по игле шприца с внутренним диаметром D = 0,3 мм, при которой сохраняется ламинарный характер течения.

12. Найти объемную скорость жидкости в игле шприца. Плотность жидкости - ρ; ее вязкость - η; диаметр и длина иглы D и L соответственно; сила, действующая на поршень, - F; площадь поршня - S.

Интегрируя по r, получим:

Пусть поршень шприца движется под действием силы F со скоростью u. Тогда мощность внешней силы N_F = Fu.

Суммарная работа всех сил равна изменению кинетической энергии. Следовательно,

Подставив найденное значение AP во второе уравнение, получим все интересующие нас величины: скорость поршня и, объемную скорость кровотока Q, скорость жидкости в игле v.