ГЛАВА 7. МАТЕМАТИЗАЦИЯ ТРУДНО ФОРМАЛИЗУЕМЫХ ОБЛАСТЕЙ

По правде говоря, мне страшно браться за эту главу. Во-первых, потому, что я не математик. Во-вторых, потому, что над этой проблемой давно и малоуспешно ломают головы многие лучшие математики мира.

Число разнообразнейших предложений и публикаций на эту тему очень велико, и я не считаю себя вправе даже пытаться их анализировать.

Один из крупнейших математиков современности И. М. Гель-фанд (с которым я неоднократно беседовал), много лет занимавшийся вместе со своими сотрудниками разработкой использования математических методов в диагностике некоторых заболеваний и добившийся также некоторых (весьма скромных) успехов, как-то сказал: "Главная задача математики в медицине изгнать из медицины всю математику". Будем расценивать эту формулировку как парадоксальную по форме, но весьма глубокую по смыслу. Кстати, он же на одном из своих семинаров заметил: "Математики плохо знают математику, а медики - медицину". С этим нельзя не согласиться, поскольку современные математика и медицина настолько многосторонни и широки, что осознать, а тем более запомнить все, что они включают, даже самому талантливому человеку практически не под силу.

Применительно к медицинской информатике я бы перефрази-ровал это высказывание так: "Беда в том, что математики совсем не знают медицину, а медики совсем не знают математику". Это правило. Счастливые исключения есть, но они крайне редки - на всю огромную область информатизации медицины и здравоохранения их не хватает. Следствием же является взаимное непонимание и общение на разных языках, что неизбежно влечет за собой трудности в разработках информационных систем и иных программных средств медицинского назначения. И, к сожалению, нередко - низкое их качество.

Я также много лет занимался разработкой автоматизированных систем компьютерной диагностики ряда заболеваний в неотложной абдоминальной хирургии. Это была совместная творческая работа с молодыми математиками-программистами. Столкнувшись с такими же трудностями, я прочел им специальный курс лекций по этой предметной области, адаптированный к их базовому образованию, после чего дело пошло быстрее и успешнее.

Некоторые результаты и выводы приведены в соответствующих главах Специальной части этой книги. Накопленный опыт и изучение литературы позволили мне сформировать собственную точку зрения на эту проблему, во многом отличающуюся от общепринятой. С ней я и ознакомлю читателей.

Математика развивалась и усложнялась по мере совершенствования и углубления знаний о мире для адекватного формального описания материальных объектов, отношений между ними и происходящих с ними процессов. Эти этапы легко проследить. Между тем - и многие специалисты это подтверждают - математический аппарат для адекватного формального описания чрезвычайно специфических биологических (живых) объектов пока не разработан. Не все даже уверены, что он возможен и даже вообще нужен. Используемые методы в ряде сугубо локальных случаев оказываются чрезвычайно полезными, но в целом это попытка использования инструментов (и воззрений) нижнего системного уровня для анализа и описания объектов верхнего уровня. Хорошо известно, что это принципиально невозможно.

Математика - это язык. И описать с его помощью удается далеко не все. Этот язык специфичен. И очень многие, в том числе количественные понятия гораздо полнее и содержательнее описываются не символическим, формальным, а естественным языком. Недаром заманчивая идея Л. А. Заде о нечетких множествах получила такой широкий профессиональный отклик. Однако, несмотря на разработанную им формализацию нечетких описаний и использование их в различных локальных предметных областях, универсальной практической реализации она так и не получила - опять-таки из-за отсутствия соответствующего универсального формального аппарата. Именно поэтому целый ряд наших количественных представлений об объектах, событиях и отношениях между ними, а также о системах тех или иных предпочтений, особенно при выборе решений об образе действия, представлены в достаточной для этого словесной (лексикографической) форме.

Пример При оценке размерности характеристик различных объектов или предпочтений, не обозначаемых конкретным числом, обычно используется 7-степенная шкала:

- все - очень много - много - средне - мало - очень мало - ничего (ничто);

- (смешанная форма): один - два - несколько - много;

- огромный - очень большой - большой - средний - малый - очень малый - ничтожный;

- прекрасно - очень хорошо - хорошо - все равно - плохо - очень плохо - катастрофично;

- это оно - очень похоже - похоже - непонятно - не похоже - совсем непохоже - не оно;

- ужасно - очень страшно - страшно - безразлично - не страшно - совсем не страшно - очень мило и т. п.

Никакие вычислительные процедуры с этими нечеткими множествами (интервальными оценками) не производятся. Данные отношения транзитивны и они могут определять порядок предпочтений:

- И - истина, правда; Л - ложь (неправда, обман);

- утверждение или согласие - да; отрицание или несогласие - нет; сомнение - ни да, ни нет (сомнение, как и вероятность, как и предпочтительность либо нежелательность могут быть выражены по 7-степенной шкале).

Для мотивов осознанного выбора образа действия (желание, возможность, запрет, необходимость) более целесообразны 3-сте-пенные и даже 5-степеные шкалы. Например:

- нельзя - все равно - можно;

- безусловно смогу - смогу - смогу ли? - пожалуй, не смогу - безусловно не смогу и т. д.

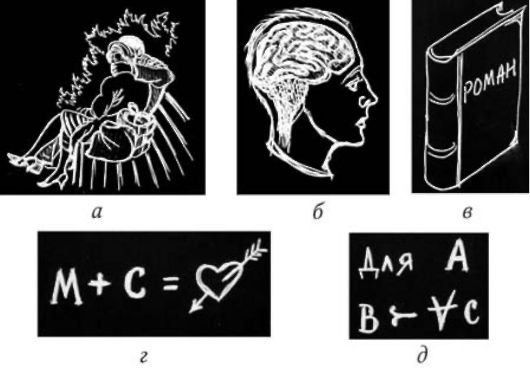
Рис. 7.1:

а - на рисунке Х. Бидструпа показано одно из проявлений любви; б - мысленное ее отображение формируется индивидуально в ЦНС - от головного до спинного мозга ("каждый понимает в меру своей испорченности"); в - варианты лингвистического ее моделирования представлены в художественной литературе: Толстой, Чехов, Мопассан и все остальные авторы пишут об одном и том же по-разному. Тема не исчерпана; г - ненаучная, но вполне понятная всем формализация, ее можно увидеть на стене дома или на заборе; д - научная формализация (Акофф Р., Эмери Ф. "О целеустремленных системах", 1974): если А любит В, то для А В предпочтительнее любого другого С

Математика - это наука. В отличие от естественных наук, изучающих объекты реального мира, математика (как и философия, богословие) изучает саму себя.

Приведу простейший пример математического описания одного из самых сложных жизненных явлений.

Наглядно показано, что мы приобретаем и что теряем при математизации этого не до конца осмысленного острого биологического и психологического умопомрачения.

Какой должна была бы быть математика для более адекватного формального описания биологических и медицинских объектов?

Ниже представлена еще одна попытка сформулировать главные требования к основам математического аппарата, в какой-то мере отображающего специфику биологических объектов для их более адекватного формального описания. Эти требования обусловлены различными свойствами объектов и представлены по отдельности, поскольку их совокупное описание является пока не решенной самостоятельной задачей.

1. Все биологические объекты обладают свойством изменчивости. Это не только эволюционная изменчивость, но и непрерывное изменение всех без исключения параметров в связи с процессами обмена веществ и взаимодействия с внешней средой в реальных пространственно-временных (st) интервалах.

Аксиома 1. Состояние биологического объекта А в sti не может быть тождественным состоянию объекта A в stj. Вывод: ни одно из формальных описаний любого биологического объекта А не может быть адекватным более одного раза (вообще говоря, и небиологического объекта тоже).

2. Все биологические объекты неоднородны.

Аксиома 2. Знаки равенства и тождества между любыми параметрами любых двух и более биологических объектов неправомерны (и небиологических тоже - это более или менее допустимая условность).

3. Все биологические объекты, с точки зрения человека, классифицируются. Целесообразно использовать знаки принадлежности объекта (объектов) к некоторому классу (классам), придавая каждому из них свои формальные обозначения.

4. Целесообразно использовать знаки сходства двух и более объектов, в том числе и вместо обозначения их математического подобия.

5. Целесообразно ввести обозначение аналогичности объектов и процессов по какому-либо искусственно заданному (произвольному) набору их сходных свойств.

6. Целесообразно ввести обозначение заменяемости объектов и процессов по какому-либо искусственно заданному (произвольному) набору их функций.

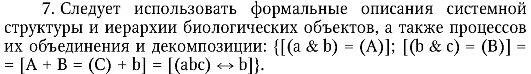
8. Учитывая тенденцию минимизации затрат любых видов ресурсов в биологических процессах, целесообразно учитывать это обстоятельство при их формализованных описаниях, введя понятие эффективности:

9. Учитывая фактическую нечеткость количественных характеристик биологических объектов и биологических процессов на всех уровнях их существования и развития, следует руководствоваться принципом относительной и абсолютной достаточности этих характеристик (а также нехватки и избыточности) для достижения данных целей, в том числе и многокритериальных, с использованием интервальных оценок (вообще говоря, неоднородность материальных объектов существует на любом иерархическом уровне, что и является причиной их развития).

Аксиома 3. Любые прогностические выводы (как и результаты любых расчетов, относящихся к структуре и функциям биологических объектов) являются в некоторой мере неопределенными и далеко не всегда вероятностными.

0. При сопоставлении биологических объектов в зависимости от точки зрения целесообразно широко использовать отношения строгого и нестрогого предпочтения. Отношения транзитивности для этих объектов неправомерны, однако они могут использоваться субъектом.

. Целесообразно ввести специальные общие обозначения физиологических процессов ощущения и потребности.

2. Помимо традиционных методов выбора оптимальных решений как меры достижения цели, целесообразно использовать качественную мотивацию в формулировках желания, возможности, разрешенности (дозволенности) и необходимости с их градациями и взаимными интегрированными сочетаниями.

13. Учитывая реальную приспособительную изменчивость (адаптивность) практически всех физиологических (и патологических) процессов, целесообразно для их формального описания использовать цепочки из двух и более стандартных последовательных алгоритмов при необходимости различной структуры (с обратной связью), где алгоритм А задает изменения алгоритму В, алго-ритмВ-алгоритму С, и т. д., для решения задачи Х в изменяющихся условиях. Это принципиальный инструмент более или менее адекватного формального динамического моделирования систем биологического управления.

14. Учитывая эту же адаптивность биологических систем, целесообразно описывать их состояние в связи с изменяющимися условиями внешней среды.

15. Учитывая саморегуляционный материально-энергетический механизм гомеостаза биологических систем, целесообразно использовать понятие обеспечивающего этот механизм информационного метаболизма (термин Юнга), без чего эффективный гомеостаз оказывается невозможным. Формализация описания этого метаболизма не может сводиться только к количественным характеристикам меры информативности получаемых сигналов.

16. Учитывая, что фактические детерминистские механизмы управления и изменчивости в биологических системах из-за их сложности в большинстве своем пока остаются нераскрытыми, для сколько-нибудь приемлемого их моделирования приходится принимать вероятностными или логико-вероятностными. Отказываться хоть от какого-то внятного описания не хочется. Тем не менее нередко целесообразнее принимать их в целом как неопределенные, чем искусственно допускать упрощения, полностью искажающие их смысл.

17. Мысленное моделирование представлений о мире (рассуждения и утверждения) - это построение сценариев из имеющихся знаний по задаваемым жизнью сюжетам для выбора (в том числе для социального выбора) образа действия данным индивидом. Форма такого моделирования может быть разнообразной, в том числе математической.

1s. Общепринятые системы представлений (парадигмы) и системы правил (идеологии) меняются по мере накопления "строительного материала" - новых знаний, которые обычно опережают устоявшиеся представления и правила.

19. Живое существо находится в сложном мире, заполненном множеством (N) разнообразнейших объектов, от отношения с которыми и от отношений между которыми зависит его самосохранение и деятельность. Формальное описание этих динамических взаимо-

отношений чрезвычайно трудно, а иногда и невозможно. Было бы очень полезно, если бы новая математика решила, наконец, актуальную проблему описания таких "N-арных" отношений.

Некоторые распространенные заблуждения

Математизация биологических и медицинских систем в качестве абсолютного блага. Прикладная математика чрезвычайно полезна в биологических и медицинских исследованиях, если удается хоть как-то учесть качественное системное своеобразие этих высших иерархических уровней развития материи. К сожалению, в значительной части исследований с привлечением математического аппарата это своеобразие игнорируется и полученные на этом основании выводы и рекомендации не могут считаться ни доказательными, ни практически приемлемыми.

Компьютеризация медицины - панацея от многих несчастий. Информатика - это наука, изучающая технологию удовлетворения информационных потребностей общества (и отрасли). Данную задачу сам по себе компьютер не решает. Это человеческая проблема. Неизбежная для развития сетевых технологий тенденция к унификации и стандартизации всего и вся, в том числе историй болезни и протоколов обмена медицинскими данными, чревата серьезными опасностями безвозвратной утраты информации об индивидуальных особенностях "источников информации", имеющих важнейший содержательный смысл. И если компьютеризацией медицины занимаются в основном инженеры и математики, не знающие специфики этой сложнейшей предметной области, то опасность возрастает. Этим должны заниматься врачи, получившие серьезную подготовку по медицинской информатике. Специальность эта существует давно, но в номенклатуру врачебных специальностей до сих пор не включена.

Заключение

Накапливающиеся предметные знания о биосфере, а также в области клинической медицины дают основания утверждать: широко распространенное представление о том, что сплошная математизация этих областей с помощью сегодняшнего формального аппарата является панацеей, ошибочно. Некоторые непрофессиональные суждения о том, что следовало бы сделать, приведены автором.