Глава 5. МЕТОДЫ БИОМЕТРИЧЕСКОЙ ДИАГНОСТИКИ

Биометрические методы изучения моделей челюстей дают возможность определить топографию и выраженность морфологических нарушений при аномалиях развития челюстей и зубных рядов, помогают поставить правильный диагнози обосновать оптимальный план лечения пациента.

Все методы измерения моделей челюстей основаны на существовании закономерностей взаимоотношения размеров зубов с одной стороны и размеров зубных рядов, апикальных базисов - с другой.

5.1. Метод Пона - Линдера - Харта

Метод используется для определения ширины зубных рядов у детей в сменном и постоянном прикусе. Пон (Pont) установил наличие зависимости между суммой мезиодистальных размеров резцов и шириной зубного ряда в области первых премоляров и моляров, которую он выразил премолярным и молярным индексами: 80 и 64. Эта зависимость отражена в следующих формулах:

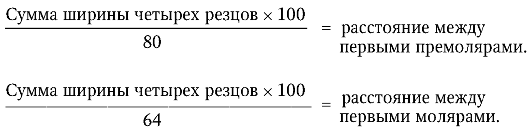
Измерительными точками на верхней челюсти являются: середина продольных фиссур первых премоляров и передняя точка пересечения продольных и поперечных фиссур первых моляров.

Рис. 8. Измерительные точки для изучения моделейчелюстей

Измерительные точки на нижней челюсти - дистальная точка первого премоляра, соприкасающаяся со вторым премоляром (точка между премолярами), и срединная точка на вестибулярной поверхности или дистально-щечный бугор первого премоляра (рис. 8, а, б).

Указанные измерительные точки, по данным Пона, используют при постоянном прикусе. В сменном прикусе вместо измерительных точек премоляров берут дистальные ямочки первых времен-

ных моляров на верхней челюсти или их дистально-буккальные бугры на нижней челюсти.

В тех случаях, когда не все верхние резцы прорезались (или отсутствуют), сумму их ширины можно определить по сумме поперечных размеров нижних резцов, используя индекс Тона (1,35), согласно которому сумма ширины верхних резцов относится к сумме нижних как ⁴/₃.

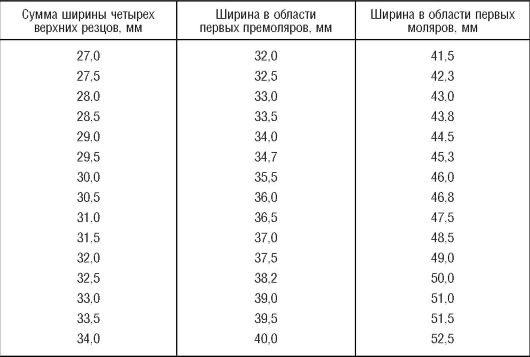
Для практических целей Пон составил таблицу расстояний между премолярами и молярами при различной ширине четырех верхних резцов. Для нижней челюсти сумму поперечных размеров четырех резцов и соответствующие расстояния между премолярами и молярами берут из таблицы верхней челюсти (табл. 3).

Немецкие ортодонты Линдер и Харт проверили данные Пона и установили, что она не может быть применима при обследовании немецких детей в силу влияния расовых особенностей. К аналогичному выводу пришла Н. Г. Снагина при обследовании детей русской национальности, поэтому указанные авторы предлагают вместо предложенных Поном коэффициентов 80 и 64 пользоваться коэффициентами 85 и 65.

Таблица 3

Зависимость ширины зубных рядов от суммы резцов

Алгоритм измерения модели верхней челюсти по методу Пона - Линдера - Харта:

1. Определить сумму ширины четырех резцов в самой широкой их части, т. е. по режущему краю (мм) с точностью до 0,1.

2. Подставить в формулу Пона показатель ширины резцов, а в знаменатель - индекс 85 (при определении ширины резцов между премолярами) или 65 (при определении ширины между молярами), вычислить искомые величины - ширину зубной дуги между премо-лярами и молярами. Искомую величину зубной дуги можно также определить по табл. 3.

3. Найти измерительные точки на первых премолярах и измерить истинную ширину зубной дуги между ними.

4. Найти измерительные точки на первых молярах и измерить истинную ширину зубной дуги между ними.

5. Сравнить истинную и искомую ширину зубной дуги (между премолярами и молярами).

6. Оценить полученные результаты: если при тесном положении передних зубов сужение зубного ряда в области премоляров и моляров больше 6 мм, показано удаление отдельных зубов. Удаление показано также в следующих ситуациях:

а) если при тесном положении резцов центральные резцы больше 10 мм, боковые - больше 7,5 мм, сумма ширины резцов составляет 35 мм и более;

б) если при узком типе лица сумма ширины резцов больше 33 мм.

5.2. Метод Коркхауза

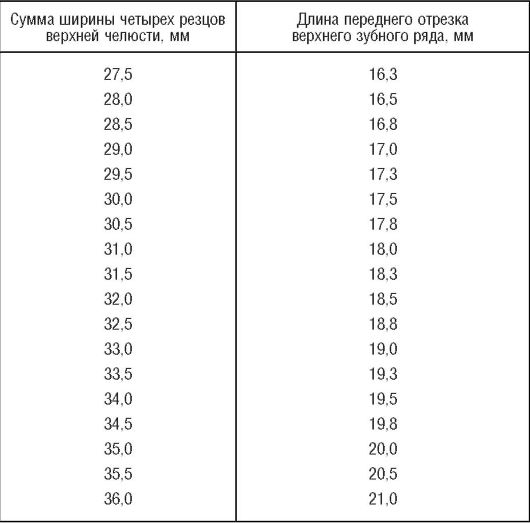
Коркхауз установил, что между суммой ширины постоянных верхних резцов и длиной переднего отрезка зубной дуги имеется зависимость, которая представлена в табл. 4.

Длину переднего отрезка верхней зубной дуги измеряют от контактной точки между центральными резцами до точки, расположенной на пересечении средней линии с линией, проведенной через передние измерительные точки по Пону, т. е. на премолярах (см. рис. 8, в, с. 54).

Алгоритм измерения модели верхней челюсти по методу Коркхауза:

1. Определить сумму ширины четырех резцов.

2. Определить длину переднего отрезка зубной дуги. Для этого на модели соединить точки Пона на премолярах, положив на них линейку. Опустить перпендикуляр от контактной точки между резцами на линию, соединяющую точки на премолярах, и с помощью штангенциркуля измерить это расстояние.

Таблица 4

Зависимость суммы четырех резцов и длины переднего отрезка верхнего зубного ряда по Коркхаузу

3. Сравнить фактическую величину переднего отрезка зубной дуги с искомой (см. табл. 4).

5.3. Метод Снагиной

Необходимое условие применения этого метода - наличие правильно отлитых моделей челюстей с полным зубным рядом (в пределах первого моляра с каждой стороны) и вестибулярной поверхностью альвеолярного отростка до переходной складки. На модели верхней челюсти должен быть также хорошо отражен рельеф твердого нёба.

Н. Г. Снагина установила, что имеется зависимость между суммой мезиодистальных размеров (шириной) 12 постоянных зубов и следующими величинами:

- шириной зубной дуги между премолярами и молярами (в точках Пона);

- шириной апикального базиса;

- длиной апикального базиса.

В норме ширина зубной дуги между первыми премолярами составляет 39,2 % от суммы ширины 12 зубов, а ширина между первыми молярами - 50,4 %. На нижней челюсти эти показатели составляют 44,3 и 56,2 % соответственно.

В норме ширина апикального базиса верхнего зубного ряда составляет в среднем 44 %, а нижнего - 43 % от суммы мезиодистальных размеров 12 постоянных зубов, а длина - соответственно 39 и 40 %.

По данным Н. Г. Снагиной, при тесном положении зубов имеется несоответствие между суммой ширины 12 зубов и параметрами апикального базиса. Ею выделены две степени несоответствия:

I степень - ширина апикального базиса верхней челюсти составляет от суммы ширины 12 зубов 42-39 % (норма - 44 %), длина - 37-35 % (норма - 39 %), на нижней соответственно 41-38 %

(норма - 43 %) и 38-36 % (норма - 40 %).

В этом случае можно рассчитывать на расширение или удлинение зубного ряда и рост апикального базиса под влиянием ортодон-тических аппаратов.

II степень - ширина апикального базиса верхней челюсти составляет от суммы ширины 12 зубов 39-32 %, длина - 37-26 %, на нижней челюсти соответственно 38-34 % и 36-31 %. В данном случае показано удаление отдельных зубов с целью уменьшения размеров зубного ряда. Расширение зубного ряда противопоказано, так как оно еще более усугубляет диспропорцию между его размерами и шириной апикального базиса.

Алгоритм измерения модели верхней челюсти по методу Сна-гиной:

1. Определить сумму ширины 12 постоянных зубов: резцов, клыков, премоляров и первых моляров.

С этой целью последовательно измеряют ширину каждого зуба в отдельности между контактными пунктами.

2. Найти искомые величины ширины зубной дуги, ширины и длины апикального базиса по методу Н. Г. Снагиной, исходя из полученной суммы ширины 12 постоянных зубов.

3. Найти передние измерительные точки по Пону между первыми премолярами и измерить истинную ширину зубной дуги между ними.

4. Найти измерительные точки на первых молярах и измерить истинную ширину зубной дуги между ними.

5. Найти самую узкую часть апикального базиса. На гипсовой модели место измерения апикального базиса находится в области переходной складки между верхушками корней клыков и первых премоляров (примерно на 8 мм ниже края десны).

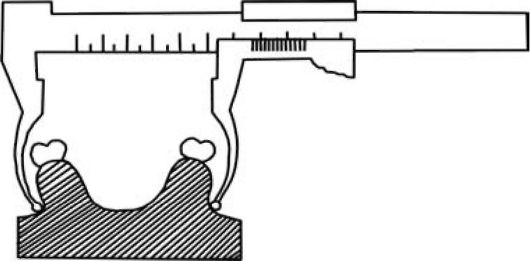
Рис. 9. Методика измерения ширины апикального базиса

6. Определить ширину апикального базиса с помощью циркуля или специального измерителя (рис. 9).

7. Определить длину апикального базиса. Для этого на модели соединить дистальные поверхности коронок первых постоянных моляров, положив на них линейку. Штангенциркулем измерить расстояние от контактной точки между центральными резцами (на десне) до пересечения срединной линии с линией, соединяющей дистальные поверхности первых постоянных моляров (см. рис. 8, г).

8. Сравнить истинные и искомые показатели ширины зубной дуги, ширины и длины апикального базиса (табл. 5).

Таблица 5

Зависимости ширинызубных рядов, шириныи длиныапикального базиса челюстей от суммы 654321 1123456 зубов, по данным Н. Г. Снагиной

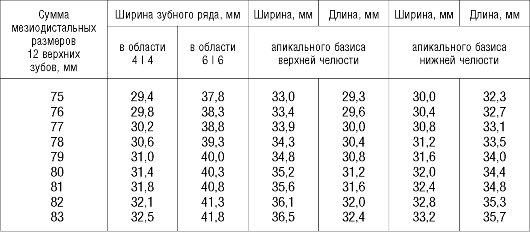
Таблица 5 (окончание)

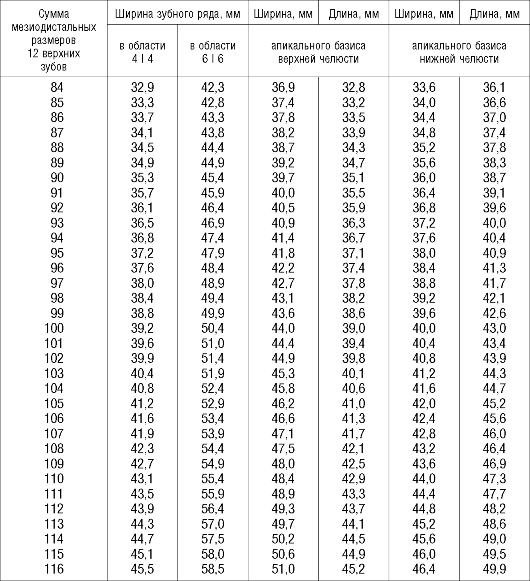
9. Подсчитать процентное отношение ширины и длины апикального базиса к сумме ширины 12 зубов, определить степень недостаточности ширины и длины апикального базиса. 10. Объяснить полученный результат.

5.4. Метод Долгополовой

З. И. Долгополова определила размеры зубных рядов у детей с временным прикусом. Антропометрическими точками боковых резцов и клыков являются нёбные (зубные бугорки), у первых и вторых моляров - место пересечения поперечной и продольной фиссур на жевательной поверхности.

Таблица 6

Средние поперечные и сагиттальные размеры зубных дуг в динамике развития у детей в возрасте от 3 до 6 лет

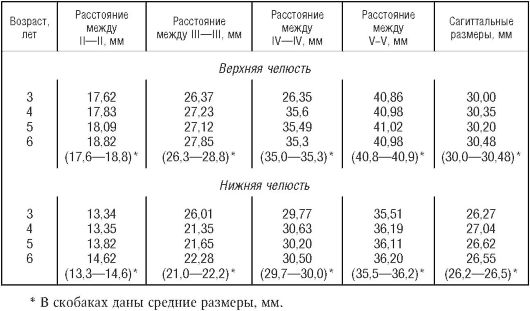
Антропометрическими точками для измерения сагиттальных размеров челюстей являются мезиальные углы центральных резцов и точка пересечения продольной и поперечной фиссур вторых моляров. Автором рассчитаны средние параметры, которые представлены в табл. 6.

Алгоритм измерения моделей методом Долгополовой:

1. Найти измерительные точки на боковых резцах, клыках, первых и вторых временных молярах (см. рис. 8, д).

2. Измерить истинную ширину зубных дуг между указанными точками.

3. Определить сагиттальный размер зубной дуги. Для этого штангенциркулем измерить расстояние между мезиальным углом коронки центрального резца и измерительной точкой на втором моляре.

4. Сравнить полученные данные с искомыми размерами по таблице.

5. Объяснить результат.

5.5. Метод Герлаха

Данный метод позволяет дифференцировать скученное положение зубов, вызванное макродентией, от скученного положения, обусловленного сужением и (или) укорочением зубных рядов. Кроме

того, с помощью этого метода можно установить причину нарушения правильных межокклюзионных контактов.

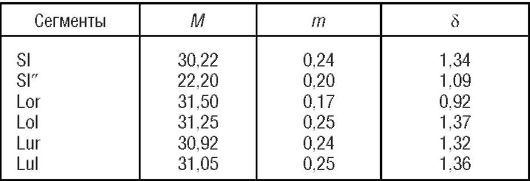
Метод основан на том, что каждый зубной ряд разделяется на сегменты: передний (включает 4 резца) и два боковых, включающих клык, премоляры и первый постоянный моляр. Величина переднего верхнего сегмента равняется сумме ширины четырех резцов, а величина нижнего переднего - произведению суммы ширины нижних резцов на индекс Тона (1,35). При прямом прикусе этот индекс равен 1,22 (по Герлаху), а при глубоком резцовом перекрытии - 1,42 (по Ю. М. Малыгину).

Соотношение сегментов Герлах представил в виде формулы:

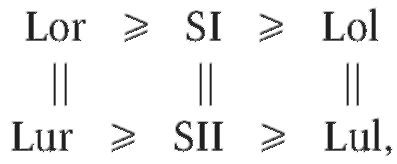
где SI - сумма ширины коронок верхних резцов; SII - величина нижнего переднего сегмента; L - длина бокового (латерального) сегмента. При обозначении каждого бокового сегмента на немецком языке использованы начальные буквы: L (Lange) - длина; о (Oberkiefer) - верхняя челюсть; u (Unterkiefer) - нижняя челюсть; γ (rechts) - правая; l (links) - левая.

Средние размеры всех сегментов приведены в табл. 7.

В норме передний сегмент меньше бокового на 10 ± 3 %. Если он равен боковому или больше его, то передние зубы располагаются тесно. Разницу в величине отдельных сегментов следует оценивать с учетом всей сегментарной формулы. Например, увеличение нижнего переднего сегмента может сочетаться с уменьшением бокового. Однако сумма всех верхних сегментов может быть равна сумме всех нижних сегментов, что обеспечивает правильные межзубные контакты.

Превалирование размеров верхних сегментов над размерами нижних обусловливает глубокое фронтальное перекрытие при ней-

Таблица 7

Средние размеры сегментов зубных рядов, по данным М. З. Миргазизова

тральном смыкании боковых зубов. Превалирование нижних сегментов приводит к возникновению обратного резцового перекрытия. Алгоритм измерения моделей по методу Герлаха:

1. Определить размер переднего верхнего сегмента по сумме ширины четырех резцов.

2. Определить размер переднего нижнего сегмента по сумме ширины четырех нижних резцов, умноженной на соответствующий индекс с учетом вида прикуса.

3. Определить размеры всех боковых сегментов, измеряя их от мезиальной поверхности клыка до дистальной поверхности первого моляра.

4. Сопоставить:

- размеры сегментов с табличными значениями;

- передний сегмент с боковыми на верхней челюсти;

- передний с боковыми на нижней челюсти;

- оба передних;

- правые боковые и левые боковые;

- все верхние сегменты со всеми нижними.

Сделать вывод по результатам измерений. Если имеется превалирование размеров переднего сегмента над боковыми или они равны, то имеющаяся скученность зубов обусловлена макродентией. Если при наличии скученности передних зубов передний сегмент меньше боковых, то ее причиной является сужение или (и) укорочение зубного ряда. Степень укорочения зубного ряда можно определить методом Фуса (см. рис. 8, е). Для этого необходимо опустить перпендикуляры из точек Пона на срединный шов, а также соединить указанные точки с контактной точкой в области резцов. Далее необходимо определить размеры катетов образовавшихся треугольников справа и слева. Разница величин указывает на степень укорочения зубного ряда.

5.6. Графические методы диагностики

Графические методы диагностики позволяют оценить форму зубных рядов, используя различные приспособления или геометрические построения (симметроскопию, фотосимметроскопию, сим-метрографию, параллелографию, диаграмму Хаулея - Гербе-ра - Гербста).

Для построения диаграммы Хаулея - Гербера - Гербста (рис. 10) необходимо:

1. Определить сумму мезиодистальных размеров трех верхних зубов (центрального, боковых резцов и клыка), что является радиусом АБ.

2. Източки Б описать круг с радиусом АБ.

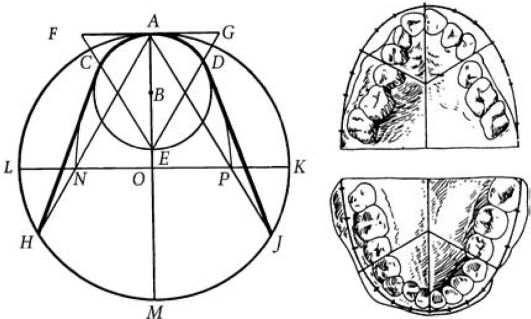
Рис. 10. Диаграмма Хаулея - Гербера - Гербста

3. На окружности радиусом АВ източки А отложить отрезки АС и АD.

Дуга САD представляет собой кривую расположения шести фронтальных зубов. Для определения расположения боковых зубов необходимо описать еще один круг. Для этого:

4. Източки Е диаметра АЕ провести прямые черезточки С и D до пересечения с касательной к окружности в точке А. Сторона полученного равностороннего треугольника EFG является искомым радиусом для вспомогательной окружности.

5. Продолжить диаметр АЕ, и отложить на нем радиус АО, равный стороне равностороннего треугольника EFG, и описать вспомогательный круг.

6. Из точки М диаметра АМ отложить радиусом АО точки J и Я.

7. Соединить точку Я с точкой С и точку J с точкой D, получить кривую HCADJ, которая является кривой зубного ряда по Хаулею.

Гербст объединил принцип Гербера, заменив боковые прямые ветви дугами CN и DP. Центрами для этих дуг являются точки L и K, лежащие на диаметре, перпендикулярном диаметру АМ. Дугу CN описывают радиусом LC, а дугу DP - радиусом KD. Таким образом, дуга Хаулея-Гербера-Гербста NCADp имеет закругленные боковые ветви и является кривой нормального верхнего зубного ряда.