Общественное здоровье и здравоохранение: учебник / Лисицын Ю.П. - 2-е изд. - 2010. - 512 с.
|
|
|
|
РАЗДЕЛ 6. ТЕОРИТИЧЕСКИЕ И МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ СТАТИСТИКИ (1)
Слово «статистика» происходит от латинского слова «status» - состояние, положение. Впервые это слово при описании состояния государства в середине XVIII века применил немецкий ученый Ахенваль.
Как наука статистика возникла в Англии в XVIII веке в трудах «политических арифметиков».
В настоящее время слово «статистика» употребляется в трех значениях.
Первое значение: статистика - это общественная наука, которая изучает количественную сторону общественных, массовых явлений в неразрывной связи с их качественной стороной.
Второе значение: статистика - это сбор цифровых, статистических данных, характеризующих то или другое общественное явление или процесс (статистическая технология).
Третье значение: статистика - это сами цифры, характеризующие эти явления и процессы.
Таким образом, «статистические данные», или «данные статистики» - цифры, которые характеризуют количественные аспекты массовых явлений, процессов, состояний.
Как наука статистика включает в себя общую теорию статистики, статистику народного хозяйства и различные отраслевые ста- тистики.
Общая теория статистики излагает общие принципы и методы статистической науки.
1 Приводятся лишь основы медицинской статистики по этапам статистического исследования. Для тех, кто желает получить более детальные сведения, рекомендуем обратиться к руководствам, например, к Руководству по социальной гигиене и организации здравоохранения под ред. Ю.П. Лисицына (М., 1987, т. 1). В разделе использованы материалы из учебного руководства под ред. Ю.П. Лисицына (1988), подготовленное К.А. Отдельновой.
Статистика народного хозяйства изучает статистическими методами народное хозяйство в целом. Ее подчас называют эконо- мической статистикой.
Отраслевые статистики изучают статистическими методами различные отрасли народного хозяйства (отрасли статистики: про- мышленная, сельскохозяйственная, транспортная, торговая, коммунальная, судебная, народного образования, демографическая, медицинская и т.д.).
Статистические методы широко применяют в различных областях знаний: в математике, физике, астрономии, биологии, меди- цине и т.д.
Как каждая наука, статистика имеет свой предмет исследования - массовые явления и процессы общественной жизни, свои методы исследования - статистические, математические, разрабатывает системы и подсистемы показателей, в которых отражаются размеры и качественные соотношения общественных явлений.
Статистика изучает количественные уровни и соотношения общественной жизни в неразрывной связи с их качественной стороной.
Математика также изучает количественную сторону тел, явлений окружающего мира, но абстрактно, без связи с качеством этих тел и явлений. Статистика возникла на базе математики и широко пользуется математическими методами. Это выборочный метод исследования, основанный на математической теории вероятности и законе больших чисел, это различные методы обработки вариационных и динамических рядов, это измерение корреляционных связей между явлениями и др.
Статистика имеет и свои собственные методы. Это метод массового наблюдения, группировок, таблиц и графиков. В литерату- ре, как правило, не проводят разграничения математических и статистических методов, применяющихся в статистике, более того, вообще говорят о статистическом методе, или о математической статистике, объединяя, таким образом, все методы, применяемые в статистике.
Главная задача статистики, как и всякой другой науки, заключается в установлении закономерностей изучаемых явлений.
Нельзя установить закономерность на основе наблюдения единичного факта, явления, для этого нужно наблюдать совокупность однородных фактов, т.е. нужно массовое наблюдение, так как закономерность проявляется только при достаточно большом числе на-
блюдений. Это основное положение закона больших чисел, на котором зиждется вся статистика и который выражает диалектику случайного и необходимого. Закон больших чисел был открыт Я. Бернулли.
Его очень наглядно демонстрирует опыт с аппаратом Гальтона. Биолог Гальтон сконструировал остроумный и очень простой аппарат, представляющий собой деревянный застекленный ящик, по внутренней стенке которого в верхней части вбиты гвозди, а в нижней части имеются перегородки. Вверху ящика есть отверстие, через которое насыпают горох или дробинки. Если бы горошины не встречали на своем пути гвозди и перегородки, то все они упали бы вертикально вниз. Однако каждая горошина встречает случайные препятствия - гвозди и перегородки и падает не обязательно вертикально вниз. Направление и место ее падения могут отклоняться и влево, и вправо от срединного положения. Никакой закономерности в падении и расположении горошин при малом их числе не выявляется.
Когда мы увеличиваем число горошин - сыплем горох струйкой, вырисовывается закономерность в их падении: больше всего горошин падает посредине, меньше всего - по краям, и чем дальше от середины, тем меньше падает горошин. Горошины, упавшие влево и вправо от середины, как бы взаимно уничтожаются, и остаются горошины, упавшие посредине, как выражение основной тенденции - закона свободно падающего тела.
Так происходит и при массовом статистическом наблюдении: основная закономерность проявляется лишь при достаточно большом числе наблюдений.
На основе закона больших чисел П. Лаплас разработал теорию вероятностей, которая рассматривает меру возможности, частоты или вероятности какого-либо явления, события или признака.
Вероятность какого-либо события равна отношению числа наступивших событий к числу всех возможных событий.
Вероятность отсутствия какого-либо события равна отношению числа ненаступивших событий к числу всех возможных событий.
В сумме вероятности наступления события и его отсутствия составляют единицу. Чем ближе вероятность наступления события к нулю, тем оно менее вероятно.
Какова вероятность того, что подброшенная монета упадет гербом вверх? Если мы подбросим монету всего 2 раза, то оба раза она может упасть гербом вниз или, наоборот, вверх. Закономерности не выявляется. Если подбросить монету 100 раз, то примерно 50
раз она падает гербом вниз, а 50 - вверх. Значит, вероятность того, что монета упадет гербом вверх, равна 1/2. Однако это выявляется лишь при достаточно большом числе наблюдений.
Как рассчитать вероятность рождения девочки? Несколько беременных могут родить только девочек. У нескольких сотен бере- менных на 100 рожденных девочек будет приходиться 106 мальчиков. Вероятность рождения девочки у каждой отдельной женщины составляет 0,48.
Назначение статистики, как и каждой науки, - вскрывать причины изучаемых явлений, поскольку все процессы и изменения в мире и обществе происходят в результате действия определенных причин.
Причинные взаимосвязи в обществе многообразны. Связи между явлениями и процессами в обществе могут быть временными, корреляционными, пространственными и др. Статистика изучает все эти взаимосвязи.
Чтобы изучать количественные закономерности, нужно сначала познать закономерности качественные, качественную сущность изучаемых явлений. Отсюда следует, что заниматься экономической статистикой должен обязательно экономист, а статистикой в каждой специальной отрасли - соответствующий специалист.
Экономическая статистика, которая изучает в целом все народное хозяйство страны, тесно связана с политической экономией, ус- танавливающей характер, сущность и законы развития экономических явлений и процессов. Экономист может и должен применять статистику только на основе глубокого понимания сущности экономических явлений, после теоретического изучения экономических процессов. В противном случае будет «игра в цифирьки». Соответственно судебной статистикой должен заниматься судебный медик, промышленной - инженер, медицинской - врач и т.д.
6.1. Медицинская статистика здоровья и здравоохранения, ее история
Одной из отраслей статистики является статистика медицинская, которая изучает количественную сторону массовых явлений и процессов в медицине.
Медицинскую и так называемую санитарную статистику не разделяют. Однако нам представляется более правильным выделить в
составе медицинской статистики статистику здоровья и здравоохранения, которую со времен земства называли санитарной статистикой.
Санитарная статистика является разделом науки об общественном здоровье и здравоохранении, в свою очередь, она состоит из статистики здоровья и статистики здравоохранения. Статистика здоровья изучает здоровье общества в целом и отдельных его групп и устанавливает зависимость здоровья от различных факторов социальной среды. Статистика здравоохранения анализирует данные о сети медицинских и санитарных учреждений, их деятельности и кадрах, оценивает эффективность различных организационных мероприятий по профилактике и лечению болезней. Статистика и статистический метод широко используются врачами в практической и научной работе.
В России медицинская статистика возникла в середине XVIII века. Передовых людей того времени волновала проблема оздоров- ления и увеличения численности населения, улучшения медицинского дела в стране.
Постоянное внимание вопросам здоровья населения одновременно с проблемами военными, хозяйственными и политическими уделял преобразователь России Петр I, по указу которого духовенству было вменено в обязанность вести учет родившихся и умерших.
Самым главным делом, которое определяет величие, могущество и богатство государства Российского, считал размножение и сохранение народа великий русский ученый М.В. Ломоносов. В письме И.И. Шувалову он писал о том, какой громадный ущерб приносит России высокая детская смертность.
Высокую детскую смертность, низкий прирост населения, угрозу «обезлюдения» некоторых местностей считал одной из основ- ных общественных проблем в России в XVIII веке первый русский профессор-медик С.Г. Зыбелин, работавший в Московском университете. Его работы служили основой и подтверждением санитарно-статистических исследований, которые сначала включались в состав медико-географических, медико-топографических и ме- дико-этнографических исследований. В этих ранних работах состояние здоровья населения рассматривалось в тесной связи с условиями внешней среды - географическими, климатическими, метеорологическими, с условиями труда, быта, питания и т.д.
Описания состояния здоровья населения России середины XVIII века В.Я. Гевитта, П.З. Кондоиди, Я.А. Чистовича стали истоками
медицинской статистики. В медико-топографических описаниях содержались сведения о численности, возрастном составе населения, рождаемости, смертности, причинах смерти. Чаще это абсо- лютные числа, но иногда приводятся относительные величины и таблицы. Описана распространенность болезней среди населения, сделана попытка объяснить причины возникновения и распространения наиболее массовых болезней, предложены меры борьбы с ними.
Таким образом,
статистика этого периода была описательной. Медико-топографические
описания конца XVIII века привели к дифференцированному изучению
состояния здоровья населения, общественных групп в связи с условиями
жизни. Эти исследования получили широкое распространение в XIX веке.
Санитарностатистическая характеристика населения в медико-топографичес-
ких исследованиях расширяется постепенно, и во второй половине XIX века
соотношения меняются - медико-топографические работы приобретают
характер комплексных санитарно-статистических описаний (Ю. Гюбнер, М.
Финкель, Ф.Ф. Эрисман). Это было обусловлено, в частности, ухудшением
санитарного состояния городов и необходимостью изучения этого явления.
Методики статистики совершенствуются. Так, группировка, а именно
вычисление показателей смертности в различных участках города позволили
Ю. Гюбнеру в
Во второй половине XIX века проводилось много комплексных социально-гигиенических исследований санитарного состояния рабочих и крестьян. Многие исследователи увязывали показатели состояния здоровья различных групп населения с экономическими показателями - размером заработной платы, продолжительностью рабочего дня, условиями труда, жилищными условиями, характером питания и т.д. (И.И. Моллесон, Ф.Ф. Эрисман, Е.М. Дементьев, А.В. Погожев, П.А. Песков, П.Ф. Кудрявцев, В.В. Святловский, Д.Н. Жбанков, С.В. Мартынов, А.И. Шингарев и др.). Эти исследователи внесли существенный вклад в изучение состояния здоровья городского и сельского населения.
С возникновением земской медицины стала развиваться земская санитарная статистика, которая уделяла основное внимание за-
болеваемости. Основы санитарной статистики заложил крупный деятель отечественной медицины Е.А. Осипов.
Выдающуюся роль в развитии русской санитарной статистики сыграл П.И. Куркин, возглавлявший в Москве санитарно-статисти- ческое бюро и ставший одним из организаторов статистической службы в советский период, автор классических работ по детской смертности, физическому развитию, заболеваемости. Ценнейшие исследования по демографической статистике принадлежат С.А. Новосельскому. Весомый вклад в развитие санитарной статистики внес П.А. Кувшинников, ставший первым академиком АМН СССР как медицинский статистик. Широкую известность в развитии статистики - ее выборочного и так называемого анамнестического методов получили работы чл.-корр. АМН СССР Г.А. Баткиса, более 30 лет заведовавшего кафедрой социальной гигиены и организации здравоохранения 2-го Московского медицинского института. Развитием наследия Е.А. Осипова, П.И. Куркина и других выдающихся санитарных статистиков стали исследования здоровья населения и статистический анализ деятельности органов и учреждений здравоохранения проф. А.М. Меркова, Е.А. Садвокасовой, а затем их учеников и последователей - чл.-корр. РАМН Е.Н. Шигана, В.К. Овчарова и др.
После революции, в первые десятилетия советской власти санитарно-статистические исследования, массовое изучение заболеваемости, но уже на основе обязательной регистрации обращений в медицинские учреждения, остаются ведущими направлениями в изучении состояния здоровья населения. Это было обусловлено практикой здравоохранения. Одновременно со становлением и развитием советской социальной гигиены и в связи с развитием профилактического направления советского здравоохранения на новых организационных основах начинаются комплексные социально-гигиенические исследования. Их число довольно значительно в первые десятилетия советской власти, особенно в 20-30-е годы, затем в 40-50-х годах они сокращаются. Число комплексных социально-гигиенических исследований, но уже нового качества, вновь увеличивается с середины 60-х годов.
Чтобы выявить зависимости состояния здоровья населения и его отдельных групп, требовались современные методики - социоло- гические, психологические, математического моделирования и др.
На кафедре социальной гигиены и организации здравоохранения 2-го МОЛГМИ в 60-90-е годы XX века и позже проведена большая
серия комплексных социально-гигиенических и так называемых клинико-социальных (Ю.П. Лисицын) исследований возрастно-половых, профессиональных групп, больных различными заболеваниями, в том числе так называемых посемейных. Эти исследования были комплексными и по кругу изучаемых вопросов, и по применяемым методам.
Дальнейшее развитие получили вопросы формирования объекта исследования, в частности, применение выборочного метода и репрезентативности выборок, способы сбора и обработки информации.
В ряде работ использован многоступенчатый отбор групп, исследуемых по программам различной сложности. Усложняются спо- собы сбора информации, совершенствуются способы ее обработки - применяются различные счетно-вычислительные машины, компьютеры, компьютерные программы разработки и анализа данных.
Медицинская статистика и ее методы необходимы при всех научных исследованиях и в практике здравоохранения. Статистические показатели - основа оценки здоровья населения, деятельности ЛПУ.
6.2. Организация и этапы медико-статистического исследования
1-й этап - составление программы и плана исследования; 2-й этап - сбор материала; 3-й этап - разработка материала; 4-й этап - анализ, выводы, предложения.
1-й этап: составление программы и плана исследования
Цель (зачем проводится исследование?) Задачи (как будет достигнута цель?)

2-й этап: сбор материала
3-й этап: разработка материала
1. Проверка собранного материала.
2. Разметка признаков по группам выбранных классификаций, шифровка (если она не проведена на этапе сбора материала).
3. Раскладка по группам.
4. Подсчет и внесение данных в таблицы.
5. Составление вариационных и динамических рядов.
6. Вычисление статистических показателей.
7. Графическое изображение данных.
4-й этап: анализ, выводы, предложения
1. Осмысление полученных абсолютных данных, графических изображений и статистических показателей, их сравнение:
- с имеющимися нормативами;
- со средними уровнями показателей;
- со стандартами, например, физического развития;
- с данными по другим учреждениям и территориям;
- в динамике.
2. Оформление работы.
3. Выводы.
4. Проверка соответствия полученных выводов принятой гипотезе и задачам исследования.
5. Предложения для внедрения в практику.
Теперь более подробно обо всех этапах исследования.
6.2.1. 1-й этап статистического исследования
6.2.1.1. Цель и задачи статистического исследования
Основная, конечная цель исследования должна быть ясна и четко сформулирована возможно раньше. С этого нужно начать составление программы и плана исследования, которые и будут его 1-м этапом, как бы его проектом, требующим от исследователя очень ответственного, творческого, вдумчивого отношения. Этот этап определяет глубину изучения темы и успех предстоящей работы.
Далее следует определить конкретные пути достижения цели. Формулировка задач исследования обычно отвечает на вопрос, как достичь цели.
6.2.1.2. Объект и единица исследования
В клинико-статистических работах всегда, а в комплексных социально-гигиенических - как правило объектом исследования яв- ляется группа людей, объединенных какими-то признаками; единица исследования - каждый человек этой группы.
Объект исследования в статистике называют статистической совокупностью, которую определяют как группу относительно однородных элементов - единиц, объединенных вместе в границах времени и пространства. Почти во всех комплексных социальногигиенических исследованиях изучаются не только группы людей, объединенных каким-то общим признаком, но и их семьи.
Являются ли семьи объектами и единицами этих исследований?
Известный советский демограф Б.Ц. Урланис предлагает различать единицу статистической совокупности и единицу наблюдений. Под единицей наблюдений он понимает ту первичную ячейку, от которой получают сведения при сборе материала. При переписи населения такой единицей является семья, при переписи оборудования - учреждение.
В социально-гигиенических исследованиях не принято дифференцировать единицу статистической совокупности и единицу на- блюдения, более того, эти два понятия отождествляются: единицу статистической совокупности называют единицей наблюдения (учета).
В социально-гигиенических исследованиях и промышленное учреждение, и школу, и больницу (ее отделения), и город мы обычно называем местом проведения исследования.
Группу обследуемых людей, здоровых или больных, можно назвать объектом исследования 1-го порядка, группу обследуемых семей - объектом исследования 2-го порядка. Единицами наблюдения в них соответственно будут человек (больной или здоровый) и семья; это исследование с двумя единицами наблюдения. Единицей социально-гигиенического исследования могут быть каждый случай заболевания при изучении заболеваемости в каком-то коллективе, каждый случай временной нетрудоспособности, смерти, рождения, травмы, инвалидности при изучении соответствующих проблем.
Практический врач или организатор здравоохранения, анализируя свою работу, составляя отчеты за тот или другой период, учи-
тывает посещаемость, обращаемость, профилактические осмотры, диспансеризацию, штаты учреждения, коечный фонд и т.д. Объектов изучения много, и в каждом из них своя единица: посещение, обращение, госпитализация и т.д. В исследовании может быть не одна, а несколько единиц исследования. Четкое и точное определение единицы исследования - очень ответственный момент, это базис всей работы. Неправильное и неточное определение единицы исследуемой статистической совокупности может стать причиной неправильных выводов.
6.2.1.3. Учетные признаки и их группировка
Учетные признаки каждой единицы наблюдения должны быть существенными признаками, непосредственно характеризующими изучаемое явление, его тип, основные черты, свойства, исходя из цели и задач исследования. Исследователь должен быть уверен, что сможет получить объективную и достаточно точную информацию.
Как признаки сходства, так и признаки различия могут быть качественными (описательными, атрибутивными) и количественными (иметь числовые выражение); по характеру взаимоотношения признаки можно рассматривать как факторные и результативные (факторные признаки влияют на признаки результативные).
Составляя перечень учетных признаков, исследователь должен сразу думать об их группировке. Это нужно и для разработки учетных документов, и для составления макетов таблиц, и для последующих этапов исследования.
Выявляемые группы должны быть качественно однородными. От того, как будут сгруппированы признаки, зависят результаты ис- следования. При этом нужно четко представлять, что должна вскрыть группировка и на каком признаке следует строить наиболее совершенную, основополагающую группировку.
Различают типологические и вариационные группировки.
Типологическая группировка - это группировка атрибутных, описательных признаков, которые выражаются словесно (пол, виды заболеваний, профессия и др.).
Вариационная группировка - это группировка количественных признаков, имеющих числовое выражение (возраст, рост, уровень дохода и т.д.).
6.2.1.4. Программа сбора материала. Место, время и объем исследования
После определения перечня учетных признаков и их группировки нужно сконструировать различные учетные документы: регист- рационные бланки, карты, анкеты, анкеты-интервью, которые и будут программой сбора материала и которые придется заполнять на каждую единицу наблюдения. На единицу наблюдения могут быть разработаны и заполнены несколько карт, анкет и т.д. Удобнее всю информацию на каждую единицу исследования (лицо) собирать на одну карту. При составлении учетных документов нужно учесть предполагаемый способ разработки материала: если планируется машинная разработка, то учетные формы должны быть согласованы с инженером-программистом
При предполагаемой ручной разработке материала рекомендуется формализация форм:

Эти вопросы тесно сопряжены с вопросом, что исследовать.
Для практического врача место проведения исследования определяется местом его работы и занимаемой должностью. Для участково- го терапевта - это терапевтический участок, для заведующего отделением - отделение, для заместителя главного врача - это ЛПУ в целом.
Научный работник при определении места исследования исходит из соображения о том, что оно должно быть типично: типичная больница, типичная поликлиника, типичный завод, типичная школа, типичный район и т.д. Только при таком условии исследование представляет ценность, т.е. его результаты будут распространяться на другие подобные учреждения, районы, города и т.д.
В научном исследовании и в практической работе можно исследовать всю имеющуюся совокупность или только ее часть.
Практический врач может анализировать все население участка, все кадры поликлиники, всех госпитализированных больных, все посещения, обращения или всех умерших в прошедшем году и т.д. Все эти исследования являются сплошными, а статистические совокупности в них - генеральными.
Если надо установить закономерность, например, посещаемости в поликлинику по дням недели, то можно анализировать не все посещения за год, а часть этих посещений. В таком случае статис- тическое исследование будет выборочным, выборочной будет и статистическая совокупность. Научные комплексные социальногигиенические и клинико-статистические исследования редко бывают сплошными и анализируют генеральные совокупности, они преимущественно выборочные и анализируют выборочные совокупности.
Важно определить, какую совокупность изучать - генеральную или выборочную, потому что численность генеральной совокупности не рассчитывается. Если совокупность будет выборочной, частью целого, т.е. генеральной совокупности, то выборочная совокупность должна быть представительна (репрезентативна) по отношению к генеральной совокупности по качеству и количеству признаков. Только в этом случае можно по части судить о целом, а выводы, полученные при изучении выборочной совокупности, перенести на всю генеральную совокупность.
Качественная представительность (репрезентативность) выборочной совокупности обеспечивается правилами выборки, количественная репрезентативность обеспечивается расчетами.
В большинстве комплексных социально-гигиенических исследований объем выборки составляет 400-800 единиц наблюдения; обычный объем клинико-статистических исследований - 100-200 больных. Необходимо учитывать относительность понятий «генеральная» и «выборочная» совокупность. Все жители Земли, все дети, все врачи, все женщины, все космонавты, все астронавты - это все генеральные совокупности. Исследователь обычно ограничивает свое исследование временем и пространством. Все женщины или все длительно и часто болеющие конкретного предприятия за кон- кретный период - генеральные совокупности с позиций данного предприятия. С позиции данной отрасли промышленности это выборочные совокупности. Значит, будет данная совокупность генеральной или выборочной, зависит, образно говоря, от высоты, с которой на нее посмотреть.
Вопрос о том, когда проводить исследование, исследователь решает по-разному в зависимости в первую очередь от сути проблемы.
Таким образом, определяя место, время и объем исследования, автор исходит, как правило, из выбора типичной статистической
совокупности, достаточной по объему, и ее наблюдения в минимально достаточное время для выявления закономерностей и тенденций изучаемых процессов и явлений.
6.2.1.5. Формирование статистической совокупности
Для обеспечения качественной представительности (репрезентативности) выборочной совокупности существуют определенные методы и способы отбора единиц исследования. В клинических, социально-гигиенических исследованиях, как правило, отобранная единица наблюдения в дальнейшем при подсчетах не участвует. Такой метод выборки в статистике называется бесповторным в отличие от повторного, когда отобранная единица наблюдения опять возвращается в генеральную совокупность и снова участвует в подсчетах. Бесповторный отбор дает более точные результаты, чем повторный.
Можно отбирать единицы совокупности (индивидуальный вид отбора), можно отбирать группы единиц (групповой вид отбора), можно сочетать тот и другой отбор, отбирая сначала группы, а в них - единицы, это будет комбинированный вид отбора.
И повторный, и бесповторный отбор единиц наблюдения может быть случайным, механическим, типологическим, серийным, парно-сопряженным, направленным и когортным.
Случайный отбор - это лотерея. Механический отбор - это каж- дый 2-й, 5-й, 10-й, по списку, по порядку и т.д. Типологический отбор - это отбор по какому-то типичному признаку - по профессии, по наличию того или иного заболевания, уровню дохода, образованию, занимаемой должности и т.д. Серийный отбор - это сочетание типологического и случайного или механического отбо- ра, когда вся совокупность делится на примерно однородные серии, затем выбираются серии и в них исследуются все единицы наблюдения. Парно-сопряженный отбор, или метод пара-копий, - это формирование, например, контрольной группы, когда каждой единице наблюдения основной группы подбирается максимально похожая на нее единица наблюдения контрольной группы. Различие должно быть только по изучаемому фактору воздействия, например, по методу лечения.
Направленный отбор по одному, двум или нескольким признакам используется для углубленного изучения взаимосвязи менее
изученных признаков при исключении признаков, влияние которых известно.
Формируются однородные по возрасту и полу группы для изучения, например, распространенности того или иного заболевания и изучается образ жизни людей этих групп. Влияние возраста и пола, таким образом, исключается.
Разновидностью направленного отбора является когортный метод, который дает возможность выявить наиболее яркие закономерности в группах лиц, объединенных тем или другим демографическим признаком.
По времени исследование может быть текущим и единовременным.
Классическим примером единовременного наблюдения в статистике является всеобщая перепись населения, которая всегда проводится на какой-то критический момент, например, на 00 ч 01.01.89. Без такого методического приема невозможно получить точные сведения о постоянно меняющейся численности населения.
Методика или техника сбора информации:
- заполнение различных учетных документов или выкопировка сведений из них (из историй болезни амбулаторных карт, различных журналов и пр.);
- непосредственное наблюдение;
- опрос (интервью, анкета, анкета-интервью). Возможно сочетание этих методик в одном исследовании.
Способы и программа разработки и анализ материала
Существуют многочисленные пакеты программ разработки и анализа для машинной разработки, которые выбирают вместе с ин- женером-программистом.
Если выбран ручной способ разработки, то программа разработки материала представляет собой перечень и макеты таблиц, которые нужно определить и разработать сейчас, а заполнить на 3-м этапе исследования, когда разрабатывают собранный материал.
Программа анализа при машинной разработке материала определена в пакетах программ разработки, программы анализа при ручной разработке материала представляют собой перечень статистических величин, которые будут получены в результате раз-
работки. Определить этот перечень тоже надо на 1-м этапе исследования.
6.2.1.6. Статистические таблицы
Статистическая таблица - наиболее удобный вид статистической сводки материала. Чтобы правильно составить макет таблицы, нужно знать как минимум следующее.
Таблица должна иметь четкое и краткое заглавие, отражающее ее содержание. Заглавие пишут над таблицей (в отличие от графика, название которого должно быть внизу).
В таблице, как в грамматическом предложении, различают статистическое подлежащее - то, о чем говорится в таблице. Это ос- новной признак изучаемого явления, он располагается, как правило, по горизонтальным строкам таблицы. Статистическое сказуемое (одно или несколько) - это то, что говорится о статистическом подлежащем, это признаки, характеризующие подлежащее, они располагаются в вертикальных графах. Оформление таблицы должно заканчиваться итогами по графам (последняя строка по горизонтали «Итого») и по строкам (последняя графа по вертикали «Всего»). Они нужны для расчета соответствующих показателей в последующем.
Таблицы бывают простыми и сложными, сложные таблицы в свою очередь - групповыми и комбинационными.
Простые таблицы дают количественную характеристику какого-то одного признака, соответственно итоговая сводка делается лишь по одному признаку.
Распределение травматологических больных по характеру повреждения (макет)
Характер повреждения | Число больных |
1. Изолированные | |
2. Множественные | |
3. Сочетанные | |
Итого... |
Сложные таблицы содержат одно подлежащее и несколько сказуемых.
В групповых таблицах подлежащее сочетается каждый раз с одним сказуемым.
Распределение травматологических больных по характеру повреждения, возрасту и полу (макет)
Характер повреждения | Пол | Возраст, годы | Всего | |||
муж. | жен. | до 30 | 30-49 | 50 и старше | ||
1. Изолированные | ||||||
2. Множественные | ||||||
3. Сочетанные | ||||||
Итого... | ||||||
В комбинационных таблицах подлежащее сочетается сразу с 2-3 сказуемыми и более, что расширяет возможности анализа. Каждая группа первого сказуемого включает все группы второго и всех следующих сказуемых. При построении комбинационной таблицы для каждого сказуемого отводится строка: 1-я строка - для групп 1-го сказуемого, 2-я строка - для групп 2-го сказуемого, 3-я строка - для групп 3-го сказуемого. Более 3-4 сказуемых использовать не рекомендуется (иначе получатся очень мелкие группы и анализ затруднится).
Распределение травматологических больных по возрасту и полу
Характер повреждений | Мужчины | Женщины | Всего | ||||
до 30 лет | 30-40 лет | 50 лет и старше | до 30 лет | 30-40 лет | 50 лет и старше | ||
1. Изолированные | |||||||
2. Множественные | |||||||
3. Сочетанные | |||||||
Итого ... | |||||||
6.2.1.7. Программа анализа. Основные свойства статистической совокупности и статистические величины, их характеризующие
После составления программы (ручной) разработки материала в виде макетов статистических таблиц нужно составить программу анализа. Основные направления анализа определяются программой разработки, но нужно также перечислить, какие статистические критерии и показатели предстоит рассчитывать при разработке материала на 3-м этапе исследования. Здесь мы только перечислим их, а методику расчета изложим ниже.
Собственно программу анализа исследователь определяет, исходя из следующих 5 основных свойств статистической совокупности:
- 1-е свойство: распределение признаков,
- 2-е свойство: средний уровень признаков,
- 3-е свойство: вариабельность - разнообразие признаков, отклонение, коэффициент вариации,
- 4-е свойство: репрезентативность - представительность признаков,
- 5-е свойство: корреляция признаков.
Все величины и показатели рассчитывают на какие-то моменты или в динамике, сравнивают между собой, по группам наблюдения, в динамике, с данными других авторов и т.д.
6.2.1.8. Особенности клинико-статистического исследования
Проведение клинико-статистических исследований имеет ряд особенностей:
- изучают клинические вопросы (эффективность медикаментозных средств, способов оперативных вмешательств и т.д.);
- единицей наблюдения является больной;
- выделяют 2 группы больных:
основную, в которой применяется новый метод лечения; контрольную, состоящую из больных, лечившихся известным ранее методом;
- регистрационным бланком является специально разработанная выборочная карта (из медицинской карты стационарного или амбулаторного больного и т.д.).
При проведении как социально-гигиенических, так и клиникостатистических исследований информацию собирают на лицо - на каждую единицу наблюдения.
6.2.2. 2-й этап. Сбор материала
На этом этапе исследователь должен собрать материал по составленной программе исследования, не отклоняясь и не искажая ее, на основе определенных методов: непосредственного наблюдения, опроса, выкопировки из различных документов, одним словом заполнения на каждую единицу исследования (в клинико-статистических исследованиях - на лицо, на больного) документа разработанной формы - анкету, выборочную карту, регистрационный бланк.
К числу трудностей сбора материала при клинико-статистических исследованиях относится работа с архивом историй болезни, особенно когда за давностью лет нужных документов не находят.
6.2.3. 3-й этап. Разработка материала
Если выбран машинный способ разработки, то, как мы уже говорили выше, разработка проводится по программе с участием про- граммиста.
Если выбран ручной способ разработки материала, то он состоит из следующих элементов.
Прежде всего, проверки всего собранного материала с точки зрения правильности и полноты ответов на все вопросы анкет, регистрационных бланков и т.д. Там, где можно, вносят дополнения и уточнения. Те карты, по которым оказалось невозможно полно и точно ответить на все вопросы, исключают из разработки.
Далее проводится разметка признаков по группам выбранных классификаций, если это не сделано в процессе сбора материала при заполнении формализованных карт, анкет и т.д. Для этого предвари- тельно должен быть разработан так называемый шифратор, т.е. перечень всех учитываемых признаков с их условными обозначениями.
Например:
Изолированная травма 1,1
Множественная травма 1,2
Сочетанная травма 1,3
и т.д.
Заполняют макеты составленных на 1-м этапе исследования статистических таблиц, для чего согласно их содержанию карты, анкеты раскладывают по группам, обозначенным в них.
Следуют подсчет и внесение данных в таблицу. В таблицах не должно оставаться пустых граф. В случае отсутствия данных ста- вятся ноль или прочерк.
Вычисление статистических показателей и критериев - ответственный момент, требующий не только знаний и умения, но и понимания сути изучаемых процессов и явлений. Конечно, машина может сделать расчеты гораздо быстрее и точнее, но только исследователь осмысленно. Более того, получение рассчитанных машиной показателей и критериев тоже требует от исследователя понимания техники расчета (см. ниже).
На 3-м этапе исследования, т.е. при разработке данных, производят подсчет полученных данных, вычисление различных показателей, коэффициентов и т.д.
6.2.3.1. Абсолютные и относительные величины
Абсолютные данные используются очень широко. Они нужны для общей характеристики явления или признака, например, чис- ленность населения в мире, в конкретной стране, в городе, районе; число врачей, учреждений здравоохранения, коек и пр.
Когда нужны сравнения, применяют относительные числа, получающиеся путем различных отношений, сопоставлений. Показатели выражаются в процентах, промилле и продецимилле и т.д., т.е. отношение тех или других величин умножается на 100 (тогда это проценты), на 1000 (тогда это промилле), на 10 000 (тогда это продецимилле) и т.д.
Нужно, чтобы показатель был удобен в использовании, выражался целой величиной. Структуру некоторых явлений выражают в процентах, показатели же рождаемости, смертности - в промилле; заболеваемость - на 1000, 10 000 или 100 000 человек населения.
Коэффициенты - это простые соотношения величин. Например, коэффициент совместительства в том или другом ЛПУ получается из соотношения числа занятых должностей (врачей, средних медработников) и числа соответствующих физических лиц.
Наиболее часто используют относительные величины: экстенсивные и интенсивные показатели, показатели соотношения и на- глядности, показатели динамического ряда.
Чтобы охарактеризовать структуру явления, показать долю признака или распределение признаков в данной совокупности, применяют экстенсивный показатель, который рассчитывают по формуле: в числителе - часть явления, в знаменателе - целое явление, умноженное на 100. Этот показатель характеризует первое свойство статистической совокупности - распределение признака, заключающееся в том, что единица статистической совокупности распределяется неодинаково по характеру учетного признака и образует определенную внутреннюю структуру.
Экстенсивными показателями являются структура смертности, структура заболеваемости, структура какой-то группы людей по возрасту или другому признаку.
Когда нужно охарактеризовать частоту (интенсивность) явления, применяют интенсивный показатель.
Типичными интенсивными показателями являются показатели рождаемости, смертности, заболеваемости в тех или иных группах людей в определенное время, обычно в показателях, кратных 10 (на 100, 1000, 10 000, 100 000). Интенсивные и экстенсивные показатели совпадают, когда вся среда продуцирует данное явление.
Например, при анализе результатов экзаменационной сессии число студентов, сдававших экзамены, принимают за 100% и определяют, какой процент получил «отлично», «хорошо», «удовлетворительно». Эти показатели сопоставимы в разные годы при условии примерно одинакового числа студентов, сдававших экзамен.
Когда нужно определить частоту признаков в сравнении с другими, вычисляем показатель соотношения по формуле: числитель - признак, знаменатель - сравниваемый признак, умножаемый на 100, 1000 или 10 000.
Типичными показателями соотношения являются обеспеченность населения койками, врачами, средними медработниками (обычно на 10 000 населения). Иногда выгодно показать отношение какогото признака к другому, принятому за 100% или за единицу. Этот показатель называют показателем наглядности. Если при расчетах не умножать, а просто сравнивать коэффициенты, то мы имеем коэффициент наглядности. Например, каждый 5-й житель нашей планеты - китаец (примерно 6 млрд населения Земли делим на 1 млрд 200 млн - население Китая, получаем 5).
6.2.3.2. Составление динамических рядов и их обработка
Если нужно и можно показать изменение изучаемого признака (ов) во времени, строят динамический ряд. Числа, из которых его составляют, - уровни ряда - могут быть абсолютными величинами. Такой динамический ряд называется простым.
Уровнями динамического ряда могут быть средние и относительные величины. Такой динамический ряд называется сложным или произвольным.
Простые динамические ряды бывают моментными и интервальными. Моментный динамический ряд состоит из чисел, характеризующих признак на определенные моменты - даты (на конец года, месяца, декады и т.д.). Уровни моментного ряда не могут дробиться.
Интервальный динамический ряд характеризует признак, изучаемый за определенный интервал времени (год, месяц, декада и т.д.). Интервальный динамический ряд можно разделить на более дробные периоды или, напротив, укрупнить интервалы. Размер интервала автор выбирает в известной мере в зависимости от степени изменчивости явления.
Простой динамический ряд (моментный).
Таблица 31. Динамика коечного фонда в районе Б. с 1991 по
Годы | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 |
Число коек | 300 | 350 | 700 | 750 | 800 | 850 |
Простой динамический ряд (интервальный).
Таблица 32. Динамика числа родившихся в районе В. за 1991-1996 гг.
Годы | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 |
Число родившихся | 500 | 450 | 440 | 425 | 400 | 350 |
Сложный (производный) динамический ряд.
Таблица 33. Динамика рождаемости и смертности в России с 1913 по
Годы | 1913 | 1981 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 |
Число родившихся на 1000 населения | 47 | 16 | 12,1 | 10,8 | 9,4 | 9,6 | 9,3 | 8,9 | 8,6 |
Число умерших на 1000 населения | 30 | 9,9 | 11,4 | 12,1 | 14,5 | 15,7 | 15,0 | 14,2 | 13,8 |
Динамический ряд, как правило, позволяет проследить основную закономерность явления - его снижение или увеличение. Уровни динамического ряда изменяются последовательно. Иногда эта последовательность нарушается, уровни динамического ряда значительно колеблются, выявить основную закономерность затруднительно. Существуют определенные приемы выравнивания уровней динамического ряда: укрупнение интервала, вычисление групповой средней, вычисление скользящей средней. Однако выравнивание уровней динамического ряда нельзя делать механичес-
ки. Это допустимо только после анализа показателей, обусловивших колебания этих уровней. Механическое выравнивание уровней динамического ряда может завуалировать причинно-следственные связи.
Если ряд состоит из величин какого-то явления за месяц, например, числа заболеваний по месяцам, то можно суммировать числа за 3 мес и дать числа заболеваний поквартально. Тогда закономерность может выявиться ярче (табл. 34).
Таблица 34. Сезонные колебания заболевания ангиной в населенном пункте Н.
Месяцы | ||||||||||||
I | Π | Ш | IV | V | VI | VII | VIII | IX | X | XI | XII | Всего |
120 | 190 | 130 | 380 | 230 | 280 | 530 | 380 | 390 | 230 | 140 | 250 | 3250 |
440 | 890 | 1300 | 620 | 3250 | ||||||||
Как видно из табл., помесячные числа заболеваний ангиной то увеличиваются, то уменьшаются. После укрупнения интервалов по кварталам года выявляется определенная закономерность: наибольшее число заболеваний приходится на летне-осенний период.
Для вычисления групповой средней для каждого укрупненного периода суммируют смежные уровни соседних периодов, а затем полученную сумму делят на число слагаемых (табл. 35).
Таблица 35. Динамика процента расхождений клинических и патолого- анатомических диагнозов в областной больнице города Н. за 1989-1996 гг.
Годы | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 |
Процент расхождения диагнозов | 12,0 | 10,8 | 9,0 | 10,2 | 9,2 | 9,6 | 9,5 | 8,9 |
Групповая средняя | 11,4 | 9,6 | 9,4 | 9,2 | ||||
Уровни динамического ряда, представленных в табл. имеют волнообразные колебания. Выравнивание ряда путем вычисления групповой средней выявило четкую тенденцию к постепенному снижению процента расхождений диагнозов в областной больнице.
Скользящая средняя вычисляется как средняя величина из данного уровня и двух соседних с ним. При вычислении скользящей средней каждый уровень ряда заменяется на среднюю величину из данного уровня и двух соседних с ним (табл. 36).
Таблица 36. Скользящая средняя
Годы | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 |
Процент расхождения диагнозов | 12,0 | 10,8 | 9,0 | 10,2 | 9,2 | 9,6 | 9,5 | 8,9 |
Скользящая средняя | - | 10,6 | 10,0 | 9,5 | 9,5 | 9,4 | 9,3 | - |
Пример расчета для
Частота расхождения клинических и патологоанатомических диагнозов в областной больнице ежегодно колебалась. Ряд, выровненный с помощью скользящей средней, выявляет постепенное уменьшение частоты расхождения диагнозов.
Чтобы проанализировать динамический ряд, нужно изобразить его графически и вычислить несколько показателей:
Если из последующего уровня вычесть предыдущий уровень, то получится абсолютный прирост (убыль).
Если этот полученный абсолютный прирост (убыль) поделить на предыдущий уровень и помножить на 100, то получится темп прироста (убыли) в процентах.
Если абсолютный прирост (убыль) поделить на темп прироста (убыли), то получится абсолютное значение 1% прироста (убыли).
Если последующий уровень поделить на предыдущий уровень и помножить на 100, то получится темп роста в процентах.
6.2.3.3. Составление вариационных рядов или рядов распределения. Расчет средних величин по способу моментов
Для облегчения и ускорения подсчетов изучаемых признаков, их средних величин распределения, разнообразия, достоверности, результатов, а также достоверности их различия в сравниваемых группах используют методику вариационных рядов.
Даже получая данные машинной обработки результатов, исследователь должен понимать, что они собой представляют.
Вариационный ряд - ряд чисел, расположенных в ранговом порядке, - обычно от меньшего к большему, реже наоборот, от боль- шего к меньшему.
В медицинской статистике приняты следующие условные обозначения для вариационного ряда:
V - варианты, числовые значения признака;
Р - частота признака, т.е. сумма вариант с данным значением признака;
n - сумма всех частот (общее число всех вариант).
Вариационные ряды бывают простыми - не сгруппированными, которые составляются, как правило, при малом (до 30) числе наблюдений, и сгруппированными, которые составляются при большом (более 30) числе наблюдений.
Основные требования к составлению вариационных рядов:
1. Расположить все варианты по порядку.
2. Суммировать единицы, имеющие одинаковый признак, т.е. найти частоту каждой варианты.
3. Определить число групп и размер интервала.
4. Разбить весь ряд на группы, используя выбранный интервал и строго соблюдая непрерывность сгруппированного ряда.
5. Дать графическое изображение.
Все 5 требований выполняют при составлении сгруппированных вариационных рядов; требования 1, 2 и 5 - при составлении не сгруппированных вариационных рядов.
Число групп в сгруппированном вариационном ряду определяется по табл. 37 в зависимости от числа наблюдений.
Таблица 37. Сгруппированный вариационный ряд
Число наблюдений | 31-45 | 46-100 | 101-200 | 201-500 |
Число групп | 6-7 | 8-10 | 11-12 | 13-17 |
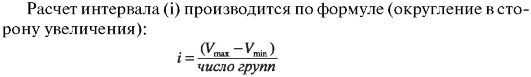
Составление простого вариационного ряда при малом и большом числе наблюдений, составление сгруппированного вариаци- онного ряда и особенности их обработки приводятся ниже.
Графическое изображение вариационного ряда помогает выявить характер распределения признака, т.е. первое свойство статистической совокупности (рис. 9).
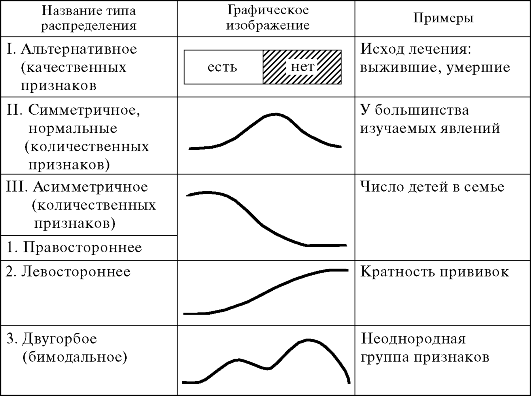
Рис. 9. Основные типы распределения признаков статистической совокупности.
Второе свойство статистической совокупности - средний уровень признака - число, являющееся обобщенной характеристикой того или другого количественного признака статистической совокупности.
Средний уровень признака определяется средними величинами:
1. Мода (Мо) - самая частая варианта.
2. Медиана (Ме) - варианта, расположенная посередине ряда.
3. Средняя арифметическая (М).


где А - условная средняя арифметическая, а = (V-A)/i - отклонение (отличие) каждой варианты от условной средней в интервалах,
i ZaP/n - первый момент средней арифметической (среднее отклонение всех вариант ряда от условной средней).
М по способу моментов вычисляется при большом числе наблюдений. Составление простого вариационного ряда и вычисление средней арифметической как средневзвешенной при большом числе наблюдений показано на примере:
Рост студентов в см V | Число студентов Ρ | VxP |
158 | 1 | 158 |
160 | 3 | 480 |
162 | 2 | 324 |
163 | 4 | 652 |
164 | 6 | 984 |
165 | 8 | 1320 |
166 | 7 | 1162 |
168 | 5 | 840 |
169 | 6 | 1014 |
170 | 5 | 850 |
172 | 4 | 688 |
174 | 2 | 348 |
175 | 2 | 350 |
176 | 1 | 176 |
ΣΡ=η=56 | ΣVΡ=9346 |
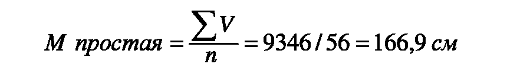
Составление группированного вариационного ряда и вычисление средней арифметической по способу моментов при большом числе наблюдений показано в табл. 38
Таблица 38.
Рост в см | V средняя | Ρ | a=(V-A)/i | АР | a2P |
Vi=3 | |||||
158-160 | 159 | 4 | -1 | -8 | 16 |
161-163 | 162 | 6 | -1 | -6 | 6 |
164-166 | 165 | 21 | 0 | 0 | 0 |
167-169 | 168 | 11 | + 1 | + 11 | 11 |
170-172 | 171 | 9 | +2 | + 18 | 36 |
173-175 | 174 | 4 | +3 | + 12 | 36 |
176-178 | 177 | 1 | +4 | +4 | 16 |
Σρ=η=56 | Σap=+31 | Σa2P=121 | |||
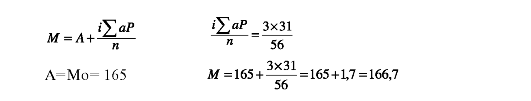
Средние величины должны характеризовать однородную статистическую совокупность.
Третье свойство статистической совокупности - разнообразие признаков: величина того или другого количественного признака неодинакова у всех единиц однородной статистической совокупности.
Это свойство иллюстрируют 3 группы мальчиков, одинаковые по численности и имеющие одинаковую среднюю арифметическую роста (табл. 39).
Среднее квадратичное отклонение (G) - учитывает разнообразие всех вариант со знаком «+» или «-» при числе признаков (n) меньше 30 (n<30):
Таблица 39.

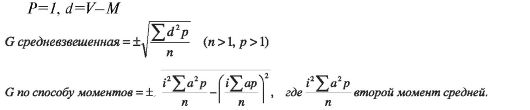
Вычисление среднеквадратичного отклонения (G) при малом числе наблюдений (n<30), например (табл. 40):
Таблица 40.
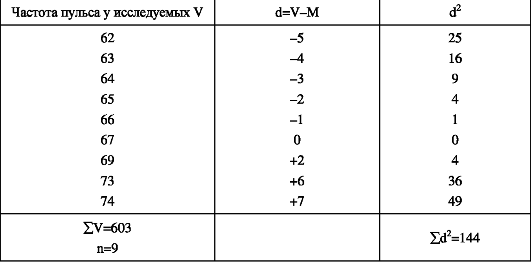
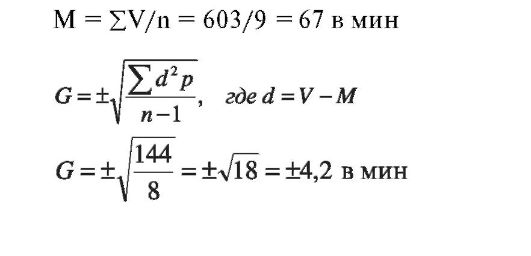
Особенности статистической обработки данных при малом числе наблюдений (n<30):
1. Средняя арифметическая находится как простая.
2. Среднее квадратичное находится как простое, n - 1.
3. Значение t находят по таблице Стьюдента.
Основной смысл названных особенностей - повышение требований к вычислениям.
Вычисление среднего квадратичного отклонения (G) при большом числе наблюдений как средневзвешенного показано на примере (табл. 41).
Таблица 41.
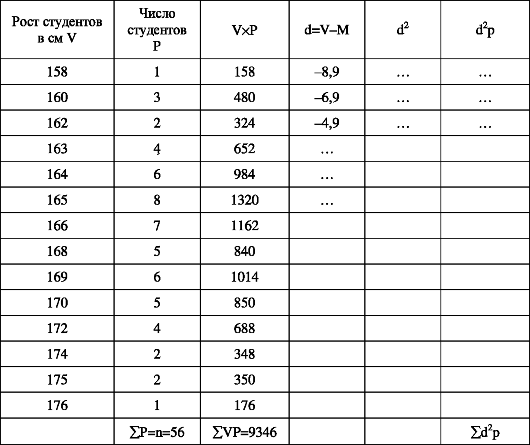
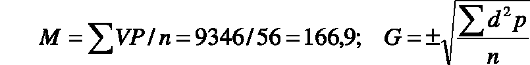
Получаются очень громоздкие вычисления, их упрощают - рассчитывают среднеквадратичное отклонение по способу моментов в сгруппированном вариационном ряду.
Вычисление среднего квадратичного отклонения по способу моментов (второй момент) показано на примере (табл. 42).
Таблица 42.
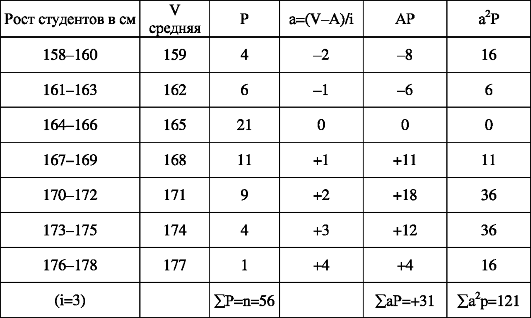
Теорией статистики установлено, что при нормальном распределении М ? σ находится 68% всех вариант, М ? 2σ находится 95,5% всех вариант, М ? 3σ находится 99,7% всех вариант (рис. 10).
По G (среднему квадратичному отклонению) можно определить структуру вариационного ряда; судить о точности (типичности) средней арифметической: если 95% всех вариант находится в пределах Μ?2σ, то средняя арифметическая является типичной (увеличивать число наблюдений не следует); судить о показателях, оценивать отдельные признаки у каждого индивидуума по стандартному отклонению t: сколько сигм составляет отклонение индивидуального признака от средней арифметической:
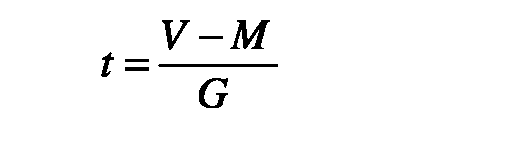
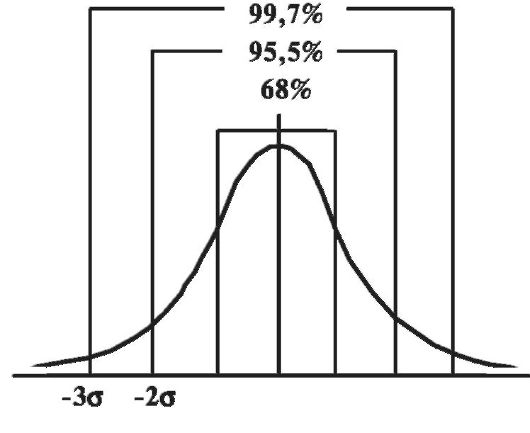
Рис. 10. Связь среднего квадратичного отклонения со структурой вариационного ряда.
Если t<2σ, то отличие индивидуального признака от стандарта незначительно; если t>=2σ, то отличие индивидуального признака от стандартного значительно.
6.2.3.4. Определение необходимого числа наблюдений
Вся мудрость статистики состоит в том, что по части можно судить о целом. Эта часть - выборочная совокупность должна быть репрезентативна, т.е. представительна по отношению к генеральной совокупности по количеству и качеству (см. ниже).
Формула определения необходимого числа наблюдений (репрезентативной выборки) выводится из формулы «ошибки» путем ал- гебраических преобразований.
Признак, по которому производится расчет, может быть выражен абсолютной или относительной величиной. Если признак вы- ражен абсолютной величиной, формула определения необходимого числа наблюдений следующая:
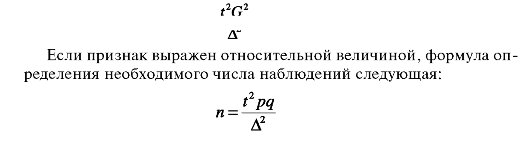
Эти формулы для случайного повторного отбора определяют самый большой объем наблюдений. Определение оптимального объема выборки в комплексных социально-гигиенических исследованиях затруднено тем обстоятельством, что единицы исследуемых совокупностей характеризуются множеством учетных признаков (трудность), так как изучается комплекс показателей здоровья различных групп населения и комплекс факторов, на них воздейству- ющих. Существующие формулы для расчета необходимого числа наблюдений основываются на конкретном единственном признаке. Вести расчет по всем исследуемым признакам невозможно.
Исследователи выделяют основной или результирующий признак и по нему рассчитывают необходимый объем наблюдений.
В ходе анализа собранного материала определяются различные параметры, характеризующие исследуемую совокупность. Это разные параметры с разной вариабельностью. Исследователи определяют их репрезентативность при одном и том же числе единиц наблюдения.
О вариабельности (G, pq) данного признака в генеральной совокупности исследователь судит по данным литературы, если они есть. При отсутствии данных литературы, если признак выражен абсолютным числом, то G определяется по данным пробного исследования, объем которого обычно составляет 30-70 единиц наблюдения. Если признак выражен относительным числом, то пробное исследование, как правило, не проводится, так как проценты вычислять не рекомендуется при числе наблюдений менее 100. В таком случае берут максимальное значение pq=0,25 (p=q=0,5) или pq=2500% (p=q=50%).
Степень уверенности в заданной неточности результата в социально-гигиенических исследованиях обычно составляет 0,95 (t=2).
Другая трудность для исследователя состоит в определении доверительного интервала (Δ), т.е. величины расхождения между средним значением признака генеральной и выборочной совокупности (Δ = Мг - Мв). Эта величина выражается в единицах изучаемого признака и характеризует допускаемую неточность искомой величины генеральной совокупности. Она задается самим исследователем в разумных пределах, исходя из сути изучаемого явления. Незначительное увеличение Δ ведет к резкому сокращению необходимого объема выборки, напротив, незначительное уменьшение Δ резко его увеличивает.
Приведем два примера расчета необходимого числа наблюдений для получения достоверного результата.
Пример 1. Сколько семей нужно исследовать, чтобы дать со- циально-гигиеническую характеристику детородной функции молодых женщин? Подобного исследования раньше не проводилось.
За результирующий признак автор взял число беременностей у молодых женщин за 5 лет брака, провел пробное исследование, оп- росив 50 женщин. Получены следующие данные:
М - среднее арифметическое число беременностей у молодых женщин за 5 лет брака составило 2;
G - среднее квадратичное отклонение = 5;
m=0,25; Δ = 0,5 (p=0,95; t=2).
Расчет проведен следующим образом:
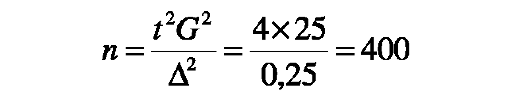
Вывод: для получения статистически достоверных социальногигиенических характеристик детородной функции молодых женщин за 5 лет брака нужно обследовать 400 семей.
Пример 2. Определить, сколько левшей необходимо взять под наблюдение для выявления среди них детей с расстройствами речи.
Доверительная вероятность 95% (0,95). Ошибка показателя не должна превышать 5%. При ранее проводившихся исследованиях расстройств речи у детей дошкольного возраста выявлено, что ими страдают 15% левшей.
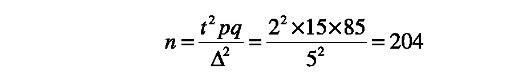
Вывод: для получения статистически достоверных данных о числе детей с расстройствами речи среди левшей нужно обследовать примерно 200 детей-левшей.
Сомнения исследователя в определении основного (результирующего) признака и его неточности (доверительного интервала) при изучении совсем не знакомых совокупностей помогает разрешить следующий прием (Плохинский Н.А., 1961):
Δ и G не определяют заранее, сразу берут ориентировочное отношение Δ/G, которое обозначают К. Это коэффициент точности,
уровень которого выбирает сам исследователь (от 0,5 до 0,1). Примерное необходимое число наблюдений в зависимости от желаемой точности и уверенности в результатах исследования приводится в табл. 43.
Таблица 43. Необходимый объем выборки
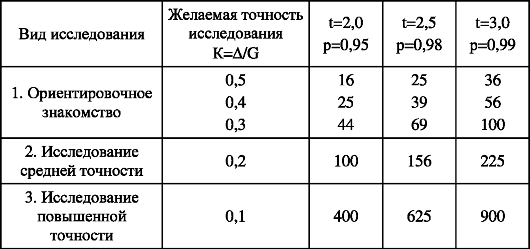
Как видно из табл., необходимый объем выборки для получения устойчивых результатов с достаточной степенью уверенности и точности составляет 400 (К=0,1; р=0,95).
В большинстве комплексных социально-гигиенических исследований на основной ступени исследования по достаточно подробной программе объем выборки составляет 400-800 единиц наблю- дения. Такие исследования вполне надежные и достаточно точные (К=0,1; р=0,95).
Однако в ходе анализа исследуемая совокупность делится на различные группы по разным признакам, репрезентативность которых определяется исследователем. Результирующий признак, положенный в основу расчета статистической совокупности, не является признаком конечной группы анализа. Бывает, что в конечных группах насчитывается лишь несколько единиц наблюдения, и параметры, их характеризующие, могут оказаться недостоверными.
Необходимое число единиц наблюдения для получения устойчивого результата при минимальной точности и достоверности со- ставляет 16-25 (К=0,4; 0,5; р=0,95).
6.2.3.5. Корреляция признаков
Пятое свойство статистической совокупности - взаимосвязь (корреляция) признаков. В природе и обществе все процессы и явления взаимно связаны. Количественные связи проявляются в функциональной и корреляционной формах.
Функциональная связь: каждому значению одного признака соответствует строго определенное значение другого признака (характерна для физико-химических явлений).
Корреляционная связь: каждому значению одного признака соответствует несколько значений другого признака (характерна для социально-гигиенических и медико-биологических процессов). Корреляционная связь проявляется лишь при массовом сопоставлении признаков в качественно однородной совокупности.
Признаки могут быть качественными и количественными несгруппированными величинами (абсолютными и производными). Задача специалиста - найти причинные связи, подтверждающие зависимость одного явления от другого или от какой-то общей причины.
Корреляция может быть представлена в виде таблиц, графика или коэффициента корреляции.
Коэффициент корреляции (r,p) дает представление о направлении (прямая +, обратная -) и силе связи (от 0 до 1): 0 - связь отсутствует; 0-0,3 - связь слабая; 0,3-0,7 - связь средняя; 0,7-1,0 - связь сильная.
Обычный, наиболее точный и часто применяемый метод (коэффициент) Пирсона:
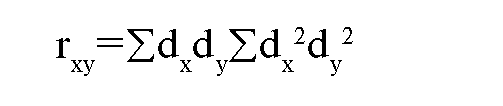
Пример вычисления

dx и dy - отклонение каждой варианты ряда «х» и «у» от их средней М.
Более грубый, приближенный и простой ранговый метод Спирмена:
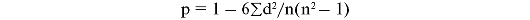
Пример вычисления

d - разность рангов; 6 - постоянный коэффициент; n - число наблюдений (сравниваемых пар).
Рангами - номерами по порядку обозначают признаки. Если признаки одинаковы, всем дается один номер - среднее суммы ран- гов этих признаков. Метод рангов применяют, если число наблюдений меньше 30; если признаки имеют не только количественное, но и качественное выражение; если ряды распределения имеют открытые варианты.
Коэффициент корреляции достоверен, если
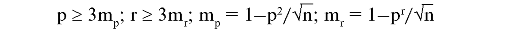
6.2.3.6. Сравнение средних абсолютных и относительных величин
Для определения достоверности одной из рассчитанных средних величин (M., M.) пользуются критерием t:
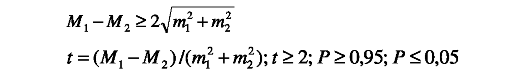
Различие между средними или относительными величинами статистически достоверно, если оно в 2 раза или более превышает корень квадратный из суммы квадратов ошибок этих средних величин.
Пример.
Первый способ оперативного вмешательства при переломе костей голени - нестабильный остеосинтез - применили у 100 боль- ных; из них осложнения возникли у 10 из них.
Второй способ оперативного вмешательства - стабильный остеосинтез применили у 200 больных, осложнения имели тоже 10 человек.
Какой способ более эффективен?
По абсолютным данным стабильный остеосинтез эффективнее, так как процент осложнений при нем меньше ровно в 2 раза. Одна-
ко закономерен ли такой вывод, иначе говоря, достоверны ли различия?
Статистическую обработку данных проводят следующим образом:
первый способ - нестабильный остеосинтез, осложнения составили 10%;
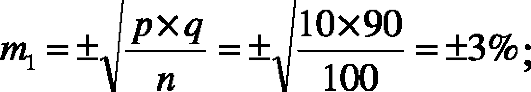
второй способ - стабильный остеосинтез, осложнения составили 5%;
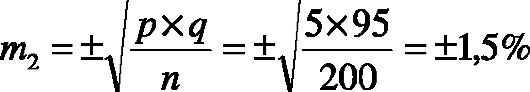
Далее находим t по формуле:
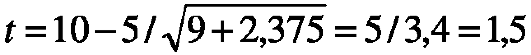
Вывод: при имеющемся числе наблюдений различие в процентах осложнений при применении различных способов оперативного вмешательства при переломе костей голени статистически недостоверно (t=1,5; р>0,05).
Чтобы сделать статистически достоверным вывод о большей эффективности стабильного остеосинтеза при переломах костей голени (меньшем проценте осложнений), нужно увеличить число наблюдений.
6.2.3.7. Метод стандартизации
Для получения более точных данных при сравнении статистических величин прибегают к методу, исключающему различия признаков этих величин (возрастно-половых и др.), т.е. к стандарту.
Существуют прямой, косвенный и обратный методы стандартизации.
Суть прямого метода состоит в вычислении общих интенсивных показателей в одинаковых признаках (единиц наблюдения), совокупностях; для чего рассчитывают частные показатели в сравниваемых группах, по которым судят об их истинном соотношении в исследуемых совокупностях; предполагают, что сравниваемые совокупности одинаковы, т.е. стандартны по составу.
Метод применяется при сравнении общих интенсивных показателей здоровья различных по составу (по полу, возрасту и другим признакам) групп населения.
Суть метода состоит в исключении влияния на общий показатель разного состава совокупностей по одному, двум признакам или более.
За стандарт принимают средний состав обеих групп, одну из сравниваемых групп или какую-то третью группу, близкую к сравниваемым.
Рассчитывают условные величины в каждой группе стандарта и общие стандартизированные показатели, которые тоже являются условными.
Если соотношение стандартизированных показателей получается иное, чем реальных, то делают вывод о том, что на уровень реальных показателей влияет разный состав сравниваемых совокупностей по стандартизуемому признаку.
Наоборот, если стандартизованные показатели повторяют соотношение реальных, то делают вывод о том, что на уровень реаль- ных показателей разный состав по стандартизуемому признаку не влияет. Рассмотрим пример прямого метода (табл.43).
Таблица 43. Распределение больных и умерших по отделениям боль- ниц А и Б (данные условные)
Отделение | Больница А | Больница Б | Стандарт больных | Больница А | Больница Б | ||||
число больных | число умерших | число больных | число умерших | летальность, % | умрет (стандарт) | летальность, % | умрет (стандарт) | ||
Терапевтическое | 600 | 30 | 200 | 12 | 400 | 5,0 | 20 | 6,0 | 24 |
Хирургическое | 300 | 6 | 700 | 21 | 500 | 2,0 | 10 | 3,0 | 15 |
Инфекционное | 100 | 4 | 100 | 5 | 100 | 4,0 | 4 | 5,0 | 5 |
В сего... | 1000 | 40 | 1000 | 38 | 1000 | 4,0 | 34 | 3,8 | 44 |
Летальность, % | 4,0 | 3,8 | Стандартизованный показатель леталь- ности | 3,4 | 4,4 | ||||
Ознакомим с другими методами стандартизации без примеров расчета.
Косвенный метод стандартизации применяется тогда, когда показатели в сравниваемых группах неизвестны или известны, но недостаточно. За стандарт выбирают какой-то хорошо известный коэффициент (но не из числа сравниваемых) такого же характера, что
и сравниваемый, и с ним с учетом его величины и структуры сравнивают имеющиеся недостоверные показатели.
Обратный метод стандартизации применяется тогда, когда необходимых для сравнения и оценки показателей нет. Их «конструируют» от «обратных» показателей, например, по данным о смертности и заболеваемости, которые следует возможно более объективно воспроизводить на основе имеющейся справочной информации численности и состава населения, среди которого и следует сравнить и определить заболеваемость и смертность.
Косвенный и обратный методы менее точны и объективны, чем прямой.
6.2.3.8. Дисперсионный анализ
Дисперсионный анализ определяет степень рассеивания (дисперсии) влияния оцениваемых признаков разных величин - пока- зателей. Он позволяет дополнительно, более полно и точно измерить силу влияния трех и более факторов, оценить разность этих факторов (средних величин или показателей), определить достоверность разности этих показателей (средних величин). Анализ дает возможность изучить и оценить влияние на конечный результат нескольких факторов или отдельных влияний. Определяется воздей- ствие среднего значения каждого фактора и средних значений при их разном сочетании.
В зависимости от числа изучаемых и оцениваемых факторов формируют однофакторный, двухфакторный, многофакторный виды дисперсионного анализа.
6.2.3.9. Графические изображения
Для наглядного представления различных статистических величин, а также для их анализа широко используют графические изображения. Практически в каждом статистическом исследовании применяется графический метод, основы которого медикам нужно знать, несмотря на широкое внедрение в последнее время компьютерной графики.
Графиками в статистике называют условные изображения числовых величин и их соотношений в виде различных геометричес- ких образов - точек, линий, плоских фигур и т.д.
Статистический график дает возможность сразу оценить характер изучаемого явления, присущие ему закономерности, особен- ности, тенденции развития, взаимосвязь его показателей.
Название графика должно кратко и точно раскрывать его содержание. Название обычно помещают под графиком в отличие от таблицы, название которой располагается над ней. Пояснительные тексты могут располагаться в пределах графического образа, рядом с ним или вне его.
Графические изображения разделяют на диаграммы, картограммы и картодиаграммы.
Диаграммой называют изображение статистических данных в виде точек, линий, плоскостей, фигур.
Диаграммы бывают:
- линейными (арифметические, полулогарифмические, полигон, гистограмма и радиальные);
- плоскостными (столбиковые, внутристолбиковые, ленточные, секторные, круговые);
- объемными (параллелепипед, куб, шар и т.д.);
- фигурными (койки, люди и т.д.).
Картограммы отражают статистические данные на географической карте.
Картодиаграммы представляют статистические данные на географической карте в виде диаграммы.
Вид графического изображения выбирается в зависимости от статистической величины.
Абсолютные величины, характеризующие статику явления, можно изобразить в виде диаграмм (плоскостной, столбиковой, объем- ной или фигурной), картограмм, картодиаграмм.
Экстенсивные показатели, характеризующие структуру явления, можно изобразить в виде секторной или внутристолбиковой плоскостной диаграммы.
Интенсивные показатели, характеризующие частоту явления, можно изобразить в виде линейной, плоскостной (столбиковой, ленточной), объемной, фигурной диаграмм.
Показатели соотношения, характеризующие отношение между двумя самостоятельными совокупностями, представляют в виде тех же графических изображений, что и интенсивные показатели.
Показатели наглядности, получающиеся из отношения ряда сравниваемых величин к одной из них, принятой за 100, графичес- ки изображают так же, как интенсивные показатели.
Обязательное правило применения графического метода - строгое соответствие каждой статистической величины виду графичес- кого изображения.
Рассмотрим правила построения диаграмм, применяемых наиболее часто.
Линейная диаграмма обычно употребляется для изображения частоты явления, изменяющегося во времени, т.е. для изображения динамики явления.
Основой для построения линейной диаграммы чаще всего является прямоугольная система координат. На оси абсцисс (X) от- кладывают, например, равные промежутки времени, а по оси ординат (Y) - показатели численности населения, заболеваемости, смертности и т.д.
Значения статистических величин наносят в виде точек на систему координат и соединяют линиями. При построении линейной диаграммы необходимо учитывать пропорции осей абсцисс (X) и ординат (Y). При отношении X:Y=4:3 искажения кривой не будет. При отношении X:Y=1:3 кривая будет сильно сжата и наоборот, при отношении X:Y=3:1 кривая будет чрезмерно растянута. И в том, и в другом случае по графику трудно правильно оценить динамику явления.
Когда на одной диаграмме изображают несколько явлений, наносят линии разного цвета или разной штриховки.
Примеры линейной диаграммы: температурная кривая, динамика рождаемости, смертности.
Радиальная диаграмма построена на полярных координатах, изображает динамику явления за замкнутый цикл времени (сутки, неделя и т.д.).
При построении радиальной диаграммы в качестве оси абсцисс используют окружность, которую делят на одинаковое число частей соответственно отрезкам времени, осью ординат служит радиус окружности или его продолжение. За радиус окружности обычно берут среднюю величину анализируемого явления. Число радиусов соответствует числу интервалов изучаемого периода: 12 радиусов при изучении явления за год, 7 радиусов при изучении явления за неделю. На каждом радиусе делают пометку, соответ-
ствующую интервалу времени, и откладывают показатели в соответствующем масштабе. Конечные точки соединяют, получается многоугольник, наглядно показывающий динамику явления.
Секторная диаграмма применяется для изображения экстенсивных показателей. Вся окружность принимается за 100% (если экстенсивные показатели выражены в процентах), при этом 1% соответствует 3,6? окружности. Затем 3,6? умножают на число процентов каждого показателя и получают размер каждого сектора в градусах. При помощи транспортира на окружности откладывают отрезки (отсчет ведут от 0?), соответствующие величине каждого показателя. Найденные точки окружности соединяют с центром круга. От- дельные секторы круга (в процентах или промилле) изображают составные части изучаемого явления.
Вместо секторной диаграммы можно применить внутристолби- ковую диаграмму, в которой ширина и высота столбика берутся произвольно. Высота принимается за 100% и в соответствующем масштабе пересчитываются экстенсивные показатели (в процентах).
Столбиковая диаграмма применяется и для иллюстрации однородных, но не связанных между собой интенсивных показателей. Столбиковыми диаграммами изображают статику явления: заболеваемость, брачность и т.д. При изображении этих явлений рисуют столбики, высота которых должна соответствовать величине изображаемых показателей с учетом масштаба. Ширина столбиков и расстояние между ними могут быть произвольными, но должны быть одинаковыми. Столбики на диаграмме могут быть вертикальными или горизонтальными (ленточными). Принципиальной разницы в методах их построения нет.
Картограмма - географическая карта, на которой отдельные территории заштрихованы с различной интенсивностью соответственно уровню интенсивного показателя.
6.4. 4-й этап статистического исследования
Заключительный этап статистического исследования - статистический анализ по программе, составленной на 1-м этапе исследования.
Собственно анализ материала проводится на всех этапах исследования: и на 1-м этапе, когда составляют программу и план, и на 2-м этапе - в процессе сбора материала. На 3-м этапе проводится
разработка материала, когда собственно и определяются основные направления анализа и рассчитываются конкретные величины, показатели, коэффициенты.
Однако анализ собранного согласно плану и программе материала выделяется и как 4-й, заключительный этап статистическо- го исследования. Он включает следующие основные элементы.
1. Осмысливание различных полученных статистических величин (абсолютных, средних, относительных, различных коэффициентов и т.д.), графических изображений. Проводят все возможные сравнения. Из них основные: сравнение с имеющимися нормативами, со средними уровнями статистических величин, со стандартами физического развития, с данными по другим учреждениям и территориям, а также сравнение в динамике.
2. Написание и оформление работы.
3. Выводы.
4. Проверка соответствия полученных выводов принятой гипотезе исследования. Каждой задаче исследования должен соответствовать конкретный, обоснованный, вытекающий из анализируемых материалов, лаконичный вывод.
5. Предложения для внедрения в практику.
6.4.1. Основные ошибки статистического анализа
Наиболее частые ошибки на 4-м этапе исследований объединяют в 3 группы: ошибки методики; неправильная оценка показателей; логические ошибки.
К ошибкам методики (первая группа) относят, прежде всего, арифметические ошибки, мысль о которых должна возникать каждый раз, когда получается неожиданный результат. Проверка и перепроверка вычислений - непременное условие всякого исследования.
Недостаточное число наблюдений ведет к получению недостоверных результатов. Исследователь должен рассчитывать необходимый объем наблюдений, чтобы застраховать себя от получения недостоверных результатов.
Нередко имеет место неправильное определение единицы наблюдения. В клинико-статистическом исследовании часто это непра- вильный диагноз.
В социально-гигиенических исследованиях неправильное определение единицы наблюдения также возможно из-за невнима-
тельности и недостаточной компетентности исследователя (неправильное определение случая заболевания, утраты трудоспособности и т.д.).
Использование слишком сложных таблиц, содержащих много признаков, ведет к тому, что получаются очень малочисленные группы и основная закономерность теряется. В комбинационных таблицах не рекомендуется иметь более 3-4 сказуемых. Следует избегать группировок признаков-подлежащих, расположенных по строкам.
Причиной неправильного анализа может быть и недостаточная обработка данных. Например, не рассчитаны относительные по- казатели, вывод делается только на основании абсолютных чисел, не составлены динамические ряды и не рассчитаны показатели, характеризующие динамику процессов, явлений, не рассчитаны коэффициенты корреляции и т.д.
Неправильности
группировки - очень частая ошибка статистического анализа. Это, прежде
всего, ошибки, имеющие в основе качественную неоднородность групп и
недоучет изменений в классификациях. Классическим примером ошибочного
вывода, связанного с качественной неоднородностью групп, является
неправильный вывод народников, отрицавших развитие капитализма в
сельском хозяйстве России. Крестьянские дворы группировали по числу душ
в семье, наделу земли, т.е. по формальному признаку, и объединяли
«вместе бедняка, который сдает землю, и богача, который арендует или
получает землю». Примером неправильного анализа, связанного с недоучетом
изменений в классификации, является анализ заболеваемости и
травматизма при разработке данных по МКБ разных пересмотров: в МКБ-10
Вторая большая группа ошибок статистического анализа - неправильная оценка показателей.
Подчас происходит смешение экстенсивных и интенсивных показателей. Вывод о большей или меньшей частоте каких-то явле- ний, процессов можно и нужно делать только на основании интенсивных показателей.
В практическом здравоохранении смешение экстенсивных и интенсивных показателей - самая частая ошибка статистического анализа.
Довольно частая ошибка статистического анализа, - когда делается вывод на искусственно неравнозначных группах. Например, испытывают новое медикаментозное средство для лечения какогото заболевания, но оно имеет определенные противопоказания. Проводят курсы лечения в соответствии с инструкцией. Однако результаты сравнивают с группой больных, которых лечили прежним методом - медикаментами, к которым не было никаких противопоказаний. Результаты несопоставимы, так как группы больных нерав- нозначны; результат мог зависеть также и от того, что больные, леченные новым методом, имели более легкую форму заболевания.
Нельзя оценивать темп роста без учета исходного уровня показателя. Существует статистическая закономерность, в соответствии с которой чем ниже исходный уровень каждого явления, тем выше темп роста, и наоборот.
Иногда представляются слишком общие сведения, преднамеренно или непреднамеренно не проводится детальный анализ материала.
К числу ошибок статистического анализа относят неиспользование метода стандартизации при анализе показателей, характери- зующих статистические совокупности, имеющие разный состав по каким-то признакам (полу, возрасту, нозологии заболеваний и т.д.).
Третья группа ошибок статистического анализа - это логические ошибки.
Иногда вывод делают на основе простого сравнения цифр без учета качественной характеристики явления. Этого недостаточно, так как статистический анализ всегда предполагает не только кон- статацию цифр по различным группам, но установление взаимосвязи с особенностями влияющих факторов и т.д.
Такой вывод нельзя считать правильным. После этого - не значит вследствие этого.
Статистический анализ - это не только анализ цифр и явлений, но в значительной мере искусство специалиста, умение выделить из ряда последовательных событий ведущие, установить достоверную связь между ними, наметить пути воздействия.
Статистический анализ будет ошибочным, если не изучены всесторонние связи явления. Эта ошибка тесно связана с предыдущими.